Rツリーインデックス

はじめに

最近インデックスのお勉強をしています
インデックスは集合論に近いと聞いて、数学出身の身からすると多少の興味は湧きます
Rツリーインデックスという地図検索で使われているインデックスの勉強をしたので、備忘録としてまとめます

Rツリーインデックスとは

• 別名空間インデックス
• 検索した図形が他の図形に含まれているか、重なるかの判定とかに使える
• RツリーのRは Rectangle のこと
• 最小外接矩形という概念を用いてインデックスを構成する
  • 最小外接矩形とはある図形をちょうど囲う長方形のこと

最小外接矩形の囲い方

◯が適当な地図とします
最小外接矩形は長方形ですので、◯を四角で囲います その四角を子ノードとして扱います

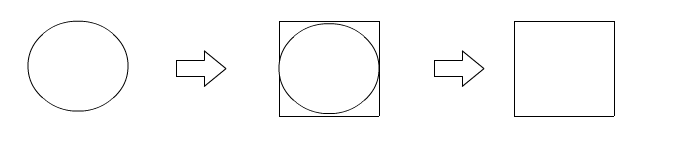
これを複数の画像に施して、適当な子ノードを親ノードにまとめます
まとめた親ノードを更にまとめて・・・を繰り返して、1個のルートノードにまでまとめます

例

3世代だとこんな感じ
最小外接矩形の最小性から、本当は親ノードと子ノードはくっついてなきゃいけないんだけど、くっついているテイで見てください
ルートノードと親ノードも同様です
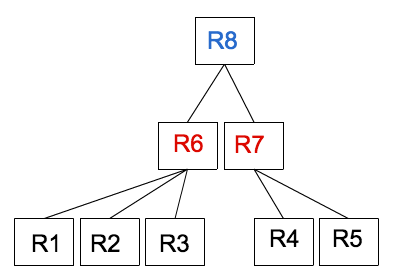
ルートノード(R8)⇒親ノード(R6,R7)⇒子ノード(R1,R2,R3,R4,R5)

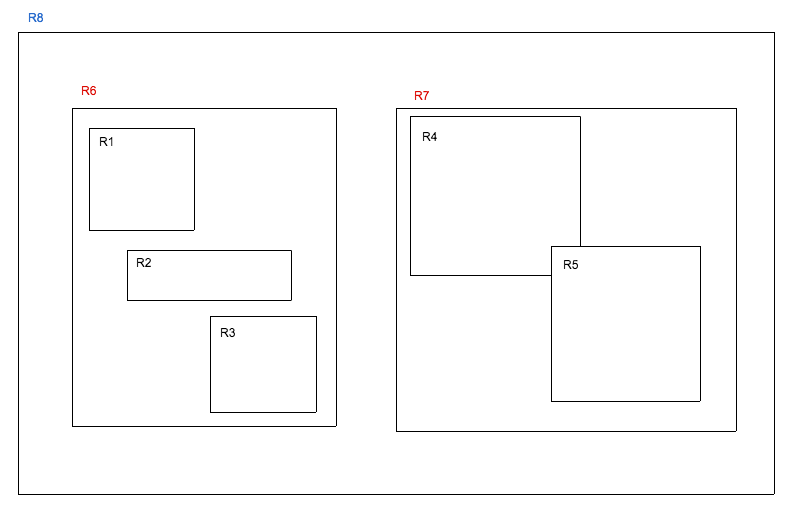
ツリー構造を書くとこんな感じです

検索

基本的にはBツリーと同じように検索します
検索する図形を黄色と赤色とする

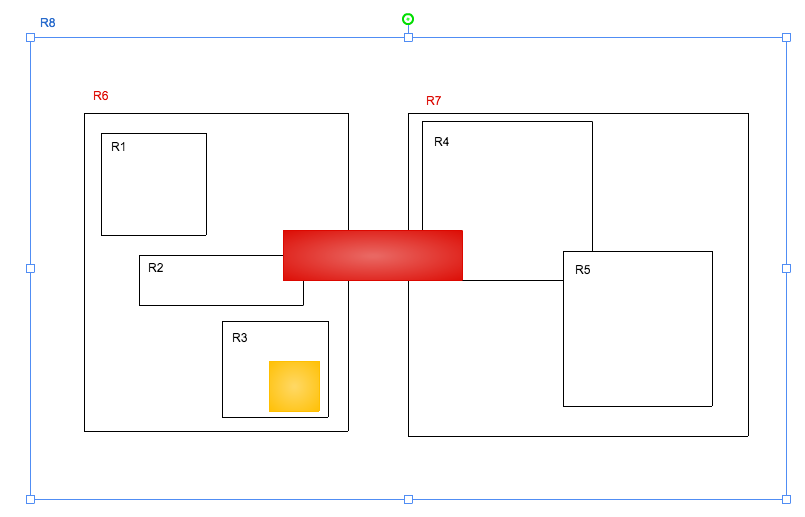
①まず黄色の場合
これはBツリーと同じように、R8⇒R6⇒R3と検索する
と言うわけではないです。
赤色探す話しを先にします

②赤色の場合
まずルートノードR8に含まれるのは明らか　これはよし
次に、R6に含まれる事を確認
Bツリーならこの後子ノードを見に行きますが
RツリーはR6に含まれる事を確認しても、R7に含まれるかを確認します。
黄色を探す時も本当はR7に含まれるか確認しています(黄色はここがBツリーと違う)

各色の検索をする際に、なめたノードをツリー構造に線を引いて表現
赤色は結局全ての子ノードに含まれていないか見ています
黄色はR7に含まれていないのでR4,R5は見ていません

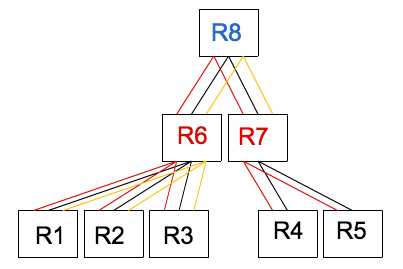
おわり

Bツリーの話しは一切しませんでした。ごめんなさい。
ザックリと自分が理解している概念を書いているので、誤りがあったらごめんなさい。
なんでここで懺悔してるんだ・・・
図形のインデックスとかもろ集合っぽくて楽しい
インデックスが楽しいと言うか集合が楽しい
学生やってた頃が懐かしい。。
早く集合の考え方を社会に活かしたいものですね。