クワイン・マクラスキー法とペトリック法による論理圧縮アルゴリズムをCで実装

概要

論理回路を設計する際、真理値表から最小論理を導くことは回路規模や動作速度に影響する。
そこで真理値表を入力とし、最小論理式を出力とする論理圧縮プログラムを作成する。論理圧縮のアルゴリズムとして、クワインマクラスキ法やペトリック法が知られている。ここではそれらを組み合わせ、さらに後述する高速化のための独自アルゴリズムを取り入れている。

高速化のための工夫

真理値表最小化アルゴリズム

論理最小化および高速化のため、プログラムの入力である真理値表を最小化するアルゴリズムを追加する。下記の真理値表のAと書かれた縦一列を削除することを考える。このとき、2行目と5行目のように一致するパターンが存在するとする。例ではそれらの真理値は2行目は0、5行は1となっており、異なった値である。つまり、Aの列を削除すると論理に矛盾が生じる(同じ001100のパターンに対し、真理値が0,1の両方存在することになる)。よってA列を削除することはできない。逆に、A列を削除しても一致するパターンが無い場合、もしくは一致するパターンがあるが真理値も同じである場合、A列は削除可能である。このような判定をすべての列に対して実施し、真理値表のビット幅を低減させる。処理時間が削減されるだけでなく、余分な項が省かれて必要十分な論理式となる。

真理値表最小化アルゴリズムは削除可否判定する順番によって削除可能な列の組み合わせが変わってしまう。上述のソースコードでは左列から順に削除可否判定を行っていたが、全パターンの削除可否判定を行い、最も削除列数の多いパターンを選択するようにする。

真理値表1列削除可否の概念

削除可
A
0000000  0
0001100  0
0001101  0
1000001  1
1001100  0
1001110  1

削除不可
A
0000000  0
0001100  0←A列を削除すると001100 0
0001101  0
1000001  1
1001100  1←A列を削除すると001100 1
1001110  1

OpenMPで並列処理

並列処理することで高速化させる。
並列化の種類はsection並列とfor並列であるが、どちらの並列化がよいかはアルゴリズムによる。ここではそれぞれの並列化に対応したソースコードを作成し、実行時間を比較する。

section並列化

高速化のため、論理ペアのテーブルから上位論理ペア抽出処理と下位論理ペア重複削除処理をsection単位で並列化した。

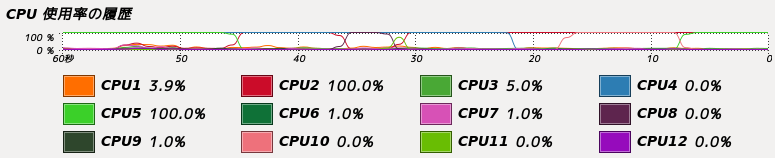
2スレッド並列なので2コアの稼働率が100%になっている。

for並列化

上位論理ペア抽出処理と下位論理ペア重複削除処理それぞれのforループを並列化した。

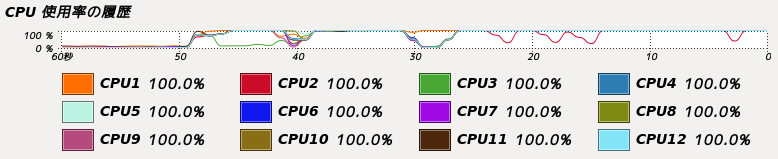
全コアで並列処理を行っていることが分かる。

実行時間比較

bit幅6~15までのtableを作成し、シングルスレッド、section並列、for並列での実行時間を比較した。

bit幅	logic_comp_single実行時間(秒)	logic_comp_openmp_section実行時間(秒)	logic_comp_openmp_for実行時間(秒)
6	0.000234	0.000133	0.000109
7	0.000313	0.000214	0.000606
8	0.000334	0.000220	0.000626
9	0.000423	0.000423	0.000917
10	0.000625	0.000629	0.001228
11	0.00315	0.00310	0.00403
12	0.215	0.179	0.112
13	7.30	4.48	2.80
14	54.1	33.3	17.3

bit幅が11以下のように小さい場合はシングルスレッドの方が高速な場合が見られる。全体の処理時間が短い場合OpenMPがコアにジョブを割り当てる時間が無視できなくなるからであると考えられる。bit幅が12以上になるとsection並列化はシングルスレッドに比べておよそ2倍の高速化になっている。2並列化の効果が得られていることが分かる。for並列化はシングルスレッドに比べて3倍程度の高速化となっている。12コアでの並列ではあるが、シングルスレッドはforループ内でパターンマッチするとbreak処理をするため、forループを12並列処理しても12倍の高速化にはならない。for並列とsection並列のどちらがより有効であるかはアルゴリズムによるが、上の結果からここではfor並列のほうが有効であることがわかったため、以降はfor並列を採用する。

bit列を数値化することで高速化

真理値表のビット列を2進数化し、文字列処理ではなく数値計算とすることで高速化した。

その他

・クイックソート
・完全オンメモリ動作
・論理圧縮中に不要となったメモリ領域を随時開放し、swapの使用を極力抑制

論理圧縮実行

ビルド

gcc -fopenmp logic_comp_openmp_for_int_opt.c -o logic_comp_openmp_for_int_opt.out -std=c99 -O3 -lm

真理値表の作成

テキストファイルに次のように記述する。
(パターン+半角スペース+真理値)
例は10bit入力の真理値表。ここではファイル名をtable_10Dとする。表に無いパターン(下記例では0000000000など)はドントケアとして扱われる。

真理値表例

0000001100  1
1000011100  1
0100011100  1
1100111100  0
0010111100  0
1010111100  0
0110111100  0
1110111100  1
0101111100  1
1101111100  1
0100000001  1
0000000011  1
1100000011  1
1101101010  1
0011101010  0
1011101010  0
0111101010  0

実行例

table_mask部に真理値表最小化アルゴリズムで削除されたbitが0で表示される。
末尾に論理式が表示される。

結果例

# ./logic_comp_openmp_for_int.out table_10D
#table_mask 1111000001
logic comp 2 ... end  15
logic comp 4 ... end  16
removing duplication 2...end : 0
logic comp 8 ... end  7
removing duplication 4...end : 1
logic comp 16 ... end  1
removing duplication 8...end : 3
[9]
[`0][`2] + [`1][`2] + [`2][3]
[0][1][2]
exec time 0.024553 s

結果の見方

　['A]=NOT(A)
　[A][B]=AND(A,B)
　[A]+[B]=OR(A,B)
　[A](改行)[B]=OR(A,B)

実行時間測定

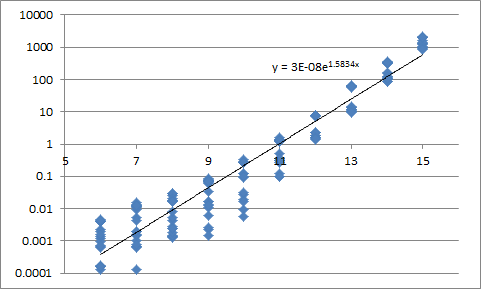
真理値表をランダムに作成し、実効時間をプロットした。横軸は真理値表のビット幅、縦軸は実効時間である。ビット幅に対して指数的に実行時間が伸びている。逆に真理値表最小化アルゴリズムでビット削減できれば指数的に時間短縮になることがわかる。

メモリリーク確認

ソースコード中のコメントアウトを外し、-gオプションをつけてビルドする。

10://#include <mcheck.h>
1244://mtrace();
1287://muntrace();

gcc -fopenmp logic_compression_openmp_for_int.c -o logic_compression_openmp_for_int.out -lm -std=c99 -O3 -Wall -Wextra -g

mtraceのログのパス設定をする。

export MALLOC_TRACE="~/mtrace.log"

mtraceでメモリリーク確認する。

# mtrace logic_compression_openmp_for_int.out ~/mtrace.log

Memory not freed:
-----------------
           Address     Size     Caller
0x0000000000eadfb0     0x68  at 0x3c76404269
0x0000000000eb02f0     0xc0  at 0x3c764042b9
0x0000000000eb03c0    0x240  at 0x3c6bc11d03
0x0000000000eb0610    0x240  at 0x3c6bc11d03
0x0000000000eb0860    0x240  at 0x3c6bc11d03
0x0000000000eb0ab0    0x240  at 0x3c6bc11d03
0x0000000000eb0d00    0x240  at 0x3c6bc11d03
0x0000000000eb0f50    0x240  at 0x3c6bc11d03
0x0000000000eb11a0    0x240  at 0x3c6bc11d03
0x0000000000eb13f0    0x240  at 0x3c6bc11d03
0x0000000000eb1640    0x240  at 0x3c6bc11d03
0x0000000000eb1890    0x240  at 0x3c6bc11d03
0x0000000000eb1ae0    0x240  at 0x3c6bc11d03
0x0000000000eb2070    0xde0  at 0x3c764042b9

わずかにメモリリークが残っている。
今後の課題。

付録

入力テーブルのマトリックス表示

ビルド

gcc table_show.c -o table_show.out -lm -std=c99 -O3

実行例

./table_show.out table_4D_random
4,4
    0 0 1 1
    0 1 1 0

00  0 0 1 0
01  0 1 1 1
11  * 1 0 1
10  0 1 1 1

./table_show.out table_8D_random
16,16
      0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
      0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0
      0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0
      0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0

0000  * 0 * 0 * * * * 1 * * * 0 * * 0
0001  * 1 0 0 1 * * 1 0 * * 1 1 * * *
0011  0 1 * 1 * * 0 * 0 0 0 * 0 * * 1
0010  1 0 1 * 0 1 * 1 1 1 * 0 0 * * 0
0110  1 * 1 0 * 1 1 1 0 * 1 0 0 * 1 1
0111  * * 0 * * 0 0 * * 0 0 * 0 0 0 1
0101  * 0 * * 0 1 * * 1 1 0 0 * * 0 0
0100  * 1 1 * 0 * * * * 0 0 * 0 * 0 *
1100  * * 1 * 0 0 0 0 * * 0 * * 0 * *
1101  0 * 1 * 0 1 0 * 0 * 0 0 1 * * *
1111  0 * 1 0 1 1 * 1 * * * 1 1 * 0 0
1110  * * 0 0 * 0 0 1 * 0 1 1 1 1 * *
1010  1 * * 1 * * 0 * 0 * * 1 * * * 1
1011  * 1 * * * * * 1 1 * 0 * 1 0 1 0
1001  0 1 0 0 1 1 1 1 * 0 * 0 1 * 1 *
1000  * 0 1 0 * * * * 1 1 1 1 0 * * 1

論理圧縮結果チェック

ビルド

gcc logic_chk.c -o logic_chk.out -O3 -std=c99

実効例

./logic_comp_openmp_for_int.out table_10D > result
./logic_chk.out table_10D result
0000001100  1 1
1000011100  1 1
0100011100  1 1
1100111100  0 0
0010111100  0 0
1010111100  0 0
0110111100  0 0
1110111100  1 1
0101111100  1 1
1101111100  1 1
0100000001  1 1
0000000011  1 1
1100000011  1 1
1101101010  1 1
0011101010  0 0
1011101010  0 0
0111101010  0 0

結果の最右列が論理式から計算した真理値。
論理に間違いがあればNG、論理が最小でなければnot minと表示される。上の結果は論理間違いなく、最小論理であることを表している。