Pythonでモンティホール問題をシミュレーションしてみる

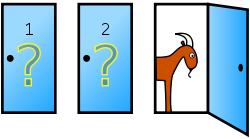
1.モンティホール問題とは？

１９９０年頃アメリカでこんなクイズ番組が放映されました。

３つのドアがあり、その内の１つのドアには新車が隠されていて、他の２つのドアにはヤギが隠されています。挑戦者が新車が隠されているドアを選ぶと、挑戦者は新車が貰えるというクイズです。

まず、挑戦者は３つのドアの内１つのドアを選びます（まだドアは開けません）。司会者はどのドアが当たりかは知っていて、挑戦者の選ばなかった２つのドアの中から、ヤギが隠されているドアを開けて見せます。そして、司会者は挑戦者にこう尋ねます、「あなたは最初に選んだドアを変更しても良いですが、どうしますか？」。

この時、挑戦者は最初に選んだドアを変更すべきかどうか、というのがモンティホール問題なのです。ちなみに、モンティホールというのは司会者の名前なんですね。

あなたは、どう思いますか。挑戦者が最初に選んだ時に新車を当てる確率は1/3に間違いはありません。その後、司会者がヤギの隠されていたドアを開けても、それは変わらず1/3のままではないか？　とか。

あるいは、司会者がヤギの隠されていたドアを開けたことで、2つのドアから新車を当てることに状況が変化したので、確率は1/2ではないか？　とか。

いずれにしても、最初に選んだドアを変更しようがしまいが、当たる確率には関係ないのではないか。

実は、これらはどれも正解ではありません。

2.天才マリリンの解答

この問題の解答をある雑誌のコラムに掲載した人物がいました。その人は、ギネスブックにも載っている世界最高のIQの持ち主である、マリリン・ボス・サバントという女性です。

彼女の解答は、「挑戦者は最初に選んだドアを変更すべきである。なぜなら、ドアを変更した場合、新車を当てる確率が2倍になるから」というものでした。

挑戦者が最初に新車が隠されているドアを選ぶ確率は1/3ですから、ドアを変更した場合に新車を当てる確率が倍になるというのは、当たる確率が1/3から2/3になると言う意見です。

当時、このコラムが発表されるやいなや、「彼女の回答は間違っている」という約1万通の大量の投書が殺到し、しかもその中には博士号を持った方も1,000人位居て大論争になったわけです。

3.どう理解すれば良いの？

もちろん、この論争はマリリンが正解の訳ですが、直感とは異なり分かりにくいですよね。

この解答は、実に色々な考え方があるので、Webで調べて見ると面白いですが、私が一番分かりやすかったのは、下記のような考え方です。

挑戦者が最初に当たりを選ぶ確率は1/3、最初に外れを選ぶ確率は2/3。最初に外れを選んだ場合は、司会者は必ず外れを選び、残されたドアは100％当たりである。従って、ドアを変更すると新車が当たる確率は2/3となる。

シンプルで明快です。外れの視点から見ると、スッキリしますね。

4.Pythonでシミュレーションしてみる

そうは言うものの、やっぱり実際にやって見ないと良く分からないわ、という方々の為に、Pythonを使って、シミュレーションしてみます。試行回数は1,000回です。

ドアを変更して勝つ回数を C_changed_wins、その確率を P_changed_wins
ドアを変更しないで勝つ回数を C_unchanged_wins、その確率を P_unchanged_wins
として、下記のコードを実行してみます。

import random 
import matplotlib.pyplot as plt

C_changed_wins, C_unchanged_wins = 0, 0  # 勝ち回数記録カウンタ初期化
P_changed_wins, P_unchanged_wins = [], []  # 確率表示リスト初期化

# 1000回シミュレーション
for i in range(1000):

    # 当たりのドアと挑戦者が選ぶドアを決める        
    truth = random.randrange(3)  # 当たりのドア ： 0, 1, 2からランダムに選ぶ      
    player_selected = random.randrange(3)  # 挑戦者が選ぶドア ： 0, 1, 2からランダムに選ぶ    
    doors_unselected = [r for r in range(3) if r is not player_selected]  # 挑戦者が選ばなかったドアを抽出

    # 司会者が選ぶドアを決める
    if player_selected == truth:  # 挑戦者が当たりを選んでいたら
        master_selected = random.choice(doors_unselected)  # 司会者は挑戦者が選ばなかったドアからランダムに選ぶ
    elif doors_unselected[0] == truth:  # 選ばなかったドアの１番目が当たりだったら
        master_selected = doors_unselected[1]  # 司会者は選ばなかったドアの2番目を選ぶ
    elif doors_unselected[1] == truth:  # 選ばなかったドアの2番目が当たりだったら
        master_selected = doors_unselected[0]  # 司会者は選ばなかったドアの1番目を選ぶ

    # 残されたドアを決める      
    doors_unselected.remove(master_selected)  # 選ばなかったドアから司会者が選んだドアを削除        
    another_door = doors_unselected[0]  # 残されたドアを決定

    # 勝ち回数をカウント  
    if another_door == truth:  # 残されたドアが当たりであれば
        C_changed_wins += 1  # 「変更したら勝ち」をカウント
    elif player_selected == truth:  # 挑戦者が選んだドアが当たりであれば
        C_unchanged_wins += 1  # 「変更しなかったら勝ち」をカウント

    # 確率推移表示用リストのデータ追加   
    P_changed_wins.append(C_changed_wins/(C_changed_wins + C_unchanged_wins))
    P_unchanged_wins.append(C_unchanged_wins/(C_changed_wins + C_unchanged_wins))

# 勝ち回数と確率の表示            
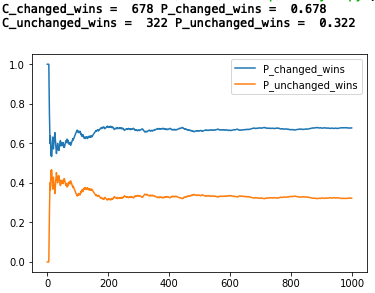
print('C_changed_wins = ', C_changed_wins, 'P_changed_wins = ',P_changed_wins[-1])
print('C_unchanged_wins = ', C_unchanged_wins, 'P_unchanged_wins = ', P_unchanged_wins[-1])

# 確率グラフ表示
plt.plot(P_changed_wins, label='P_changed_wins')
plt.plot(P_unchanged_wins, label='P_unchanged_wins')
plt.legend()
plt.show()     

1,000回試行した結果、ドアを変更した場合の確率は、67.8％と理論値の66.7％に極めて近くなりました。マリリンの言うことは本当だったことが、これで良く分かります。