Python 有村架純と綾瀬はるかは主成分分析(PCA)で見分けられるか？

1.はじめに

　前回の投稿、「Pythpn 有村架純を主成分分析(PCA)してみる」でやった、主成分分析による画像の次元削減が面白かったので、今回のテーマはそれに続いて、主成分分析による画像の識別です。

　丁度手元に、「綾瀬はるか」さんの顔画像があったので、前回使った「有村架純」さんの顔画像と合わせて、有村架純と綾瀬はるかは主成分分析(PCA)で見分けられるか、というテーマに挑戦してみたいと思います。

　あっ、私、有村架純さんのファンでも、綾瀬はるかさんのファンでもありません。たまたま、画像データが手元にあっただけです（本当に）。

2.データの準備

　カレントフォルダー(./data/arimura)に有村架純さんの顔画像223枚、カレントフォルダー(./data/ayase)に綾瀬はるかさんの顔画像185枚を用意し、カラーからモノクロに変換して、64*64ピクセルに揃えたものをデータとします。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from sklearn.decomposition import PCA
from PIL import Image
import glob
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import KernelPCA

# 初期設定
folder = ['arimura', 'ayase']
image_size = 64

# データ画像の読み込み
x = []
y = []
for index, name in enumerate(folder):
    dir = './data/' + name
    files = glob.glob(dir+'/*.png')
    for file in files:
        image = Image.open(file)
        image = image.convert('L')  # カラーを白黒に
        image = image.resize((image_size, image_size))  # image_seize * image_size に縮小
        data = np.asarray(image)
        x.append(data)
        y.append(index)
X = np.array(x)
y = np.array(y)  # arimura:0, ayase:1 
X = X.reshape(X.shape[0], image_size * image_size) 
X = X / 255.0

# 画像表示関数
def disp_data(X):
    rows, cols = 3, 10  #3行10列
    fig, aX_invs = plt.subplots(ncols=cols, nrows=rows, figsize=(18, 6)) 
    for i in range(30):
        r = i // cols
        c = i % cols
        aX_invs[r, c].imshow(X[i].reshape(image_size,image_size),vmin=0.0,vmax=1.0, cmap = cm.Greys_r)
        aX_invs[r, c].set_title('data %d' % (i+1))
        aX_invs[r, c].get_xaxis().set_visible(False)
        aX_invs[r, c].get_yaxis().set_visible(False)
    plt.show()


X_arimura = X[y==0]  # 有村架純画像の指定
print('X_arimura.shape =', X_arimura.shape)
disp_data(X_arimura)

X_ayase = X[y==1]  # 綾瀬はるか画像の指定
print('X_ayase.shape =', X_ayase.shape)
disp_data(X_ayase)

有村架純、綾瀬はるかとも、データの初めから30枚を表示しています。

データの形はそれぞれ、X_arimura.shape=(223,4096), X_ayase.shape=(185, 4096）です。

for index, name in enumerate(folder): によって、'arimura'フォルダーから読み込んだ画像には y=0、'ayase'フォルダーから読み込んだ画像には y=1というインデックスを付けています。

こうすることで、X[y==0]で有村架純の画像、X[y==1]で綾瀬はるかの画像を指定することが出来ます。

3.主成分分析（PCA）による主成分画像

　まず、3次元（n_components=3）で、主成分分析(PCA)をした時の、第1主成分〜第3主成分を画像で見てみましょう。

# 主成分成画像の表示関数
def disp_components():    
    print('n_components = '+str(N))
    print('explained_variance_ratio = ', pca.explained_variance_ratio_.sum())    

    fig, aX_invs = plt.subplots(nrows=1, ncols=3, figsize=(8, 4)) 
    for i in range(3):
        aX_invs[i].imshow(pca.components_[i].reshape(image_size,image_size),vmin=-0.03,vmax=0.03, cmap = cm.Greys_r)
        aX_invs[i].set_title('component %d' % (i+1))
        aX_invs[i].get_xaxis().set_visible(False)
        aX_invs[i].get_yaxis().set_visible(False)
    plt.show()

# PCAによる主成分の画像を表示
N = 3
pca = PCA(n_components=N)

print('PCA for arimura')
pca.fit(X[y==0])
disp_components()

print('PCA for ayase')
pca.fit(X[y==1])
disp_components()

上段が有村架純、下段が綾瀬はるかの、第1主成分〜第3主成分を画像にしたものです。

両方とも、explained_variance_ratioは 41〜43％ですので、第1〜第3主成分で、全体の情報量の41〜43％をカバーしています。

64*64=4,096次元ある内のたった3次元ですから、このカバー率でも上出来でしょう。

理由は分かりませんが、有村架純のcomponent1（第1主成分）は、左右の目の大きさが違っていて、少し怖い感じです（笑）。

4.主成分分析のグラフ化

では、主成分分析（PCA）の結果を2次元グラフと3次元グラフにプロットしてみましょう。

# 2次元グラフ作成関数
def fig_2d(X):
    fig, ax = plt.subplots(figsize=(8, 8))
    ax.scatter(X[:,0][y==0],X[:, 1][y==0], c ='r',  s = 100, alpha=0.5)
    ax.scatter(X[:,0][y==1],X[:, 1][y==1], c ='b',  s = 100, alpha=0.5)
    ax.set_xlabel('1st Component')
    ax.set_ylabel('2nd Component')
    ax.legend(['arimura', 'ayase'], loc='best', fontsize=14)
    plt.show()

# 3次元グラフ作成関数
def fig_3d(X):
    fig, ax = plt.subplots(figsize=(12, 12))
    ax = fig.add_subplot(111, projection='3d')
    ax.scatter(X[:,0][y==0],X[:, 1][y==0], X[:,2][y==0], c='r', s =100, alpha=0.5)
    ax.scatter(X[:,0][y==1],X[:, 1][y==1], X[:,2][y==1], c='b', s =100, alpha=0.5)
    ax.set_xlabel('1st Component', fontsize=15)
    ax.set_ylabel('2nd Component', fontsize=15)
    ax.set_zlabel('3rd Component', fontsize=15)
    ax.legend(['arimura', 'ayase'], loc='best', fontsize=14)
    plt.show()

# PCA分析
pca = PCA(n_components=3)
X_pca = pca.fit_transform(X)
fig_2d(X_pca)
fig_3d(X_pca)

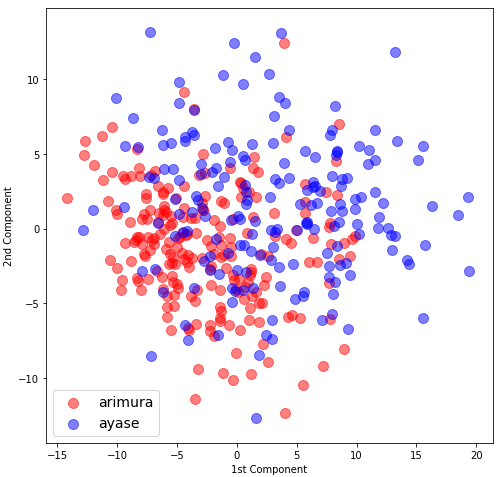
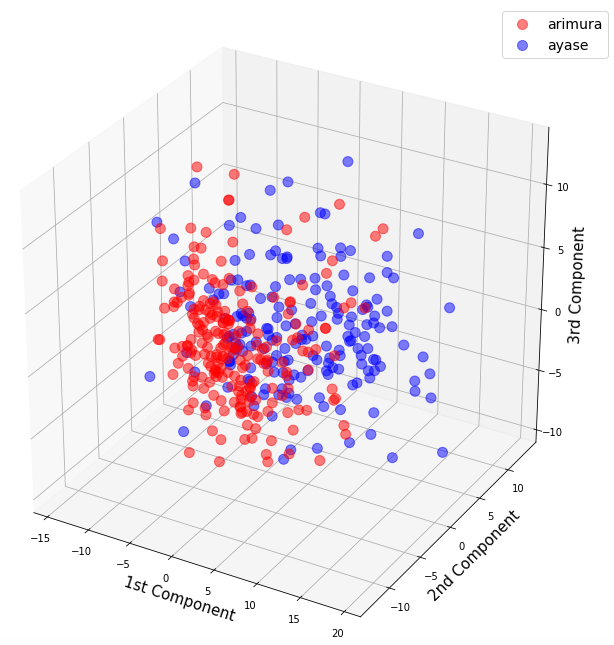
ありゃま！　2次元グラフ、3次元グラフとも、有村架純と綾瀬はるかが綺麗に混ざり合っていて、全く識別不能です。

題材を女性の顔に絞っているので、細部は色々違いはあるものの、全体の４割位のベーシックなところは、ほとんど差がないということでしょうか。

5.カーネル主成分分析

　私が勉強したテキストでは、主成分分析では歯が立たない場面では、カーネル主成分分析というのが出て来て、鮮やかにデータを分離していたので、そちらも試してみましょう。

# KernelPCA分析
pca = KernelPCA(n_components = 3, kernel='rbf', gamma = 11, random_state=10)
X_pca_k = pca.fit_transform(X)
fig_2d(X_pca_k)
fig_3d(X_pca_k)

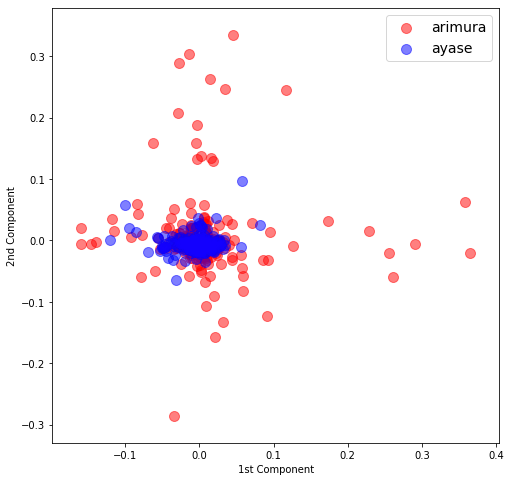
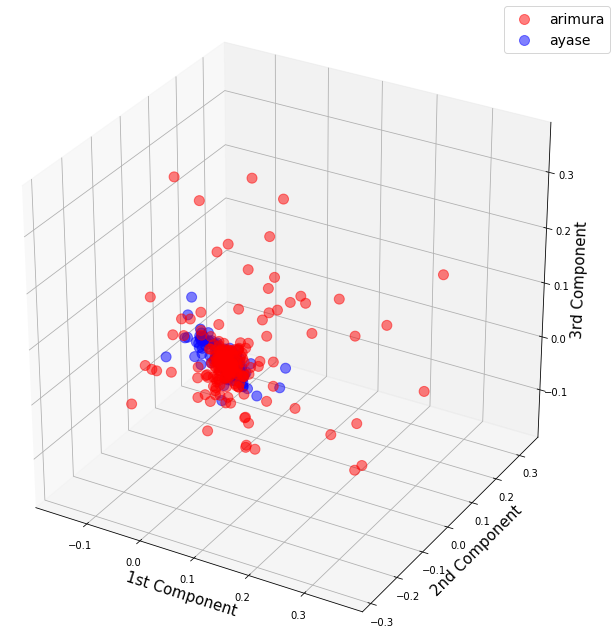
カーネル主成分分析のパラメーターgammaの適正値はケースバイケースなので、とりあえず色々な数値を入れてみました。その結果gamma=11が一番マシでした。

やー、それにしても、バラツキの大きいところに限定すればほとんど有村架純なので、なんとか見分けられそうな気がしますが、コアな部分はとても見分けがつきませんね。

6.3次元グラフの回転

　もしかしたらカーネル主成分分析の3次元グラフを別の角度から見たら、有村架純と綾瀬はるかが分かれている様に見える角度があるかもしれないと思って、念のため3次元グラフを回転させて確認してみることにしました。

# KernelPCA 3次元グラフ回転
from io import BytesIO
from PIL import Image

def fig_3d_round(X, angle):
    fig, ax = plt.subplots(figsize=(12, 12))
    ax = fig.add_subplot(111, projection='3d')
    ax.scatter(X[:,0][y==0],X[:, 1][y==0], X[:,2][y==0], c='r', s =100, alpha=0.5)
    ax.scatter(X[:,0][y==1],X[:, 1][y==1], X[:,2][y==1], c='b', s =100, alpha=0.5)
    ax.set_xlabel('1st Component', fontsize=15)
    ax.set_ylabel('2nd Component', fontsize=15)
    ax.set_zlabel('3rd Component', fontsize=15)
    ax.legend(['arimura', 'ayase'], loc='best', fontsize=14)
    ax.view_init(30, angle)  # 視点の設定
    plt.close()
    buf = BytesIO()
    fig.savefig(buf, bbox_inches='tight', pad_inches=0.0)
    return Image.open(buf)

images = [fig_3d_round(X_pca_k, angle) for angle in range(60)]
images[0].save('output.gif', save_all=True, append_images=images[1:], duration=100, loop=0)

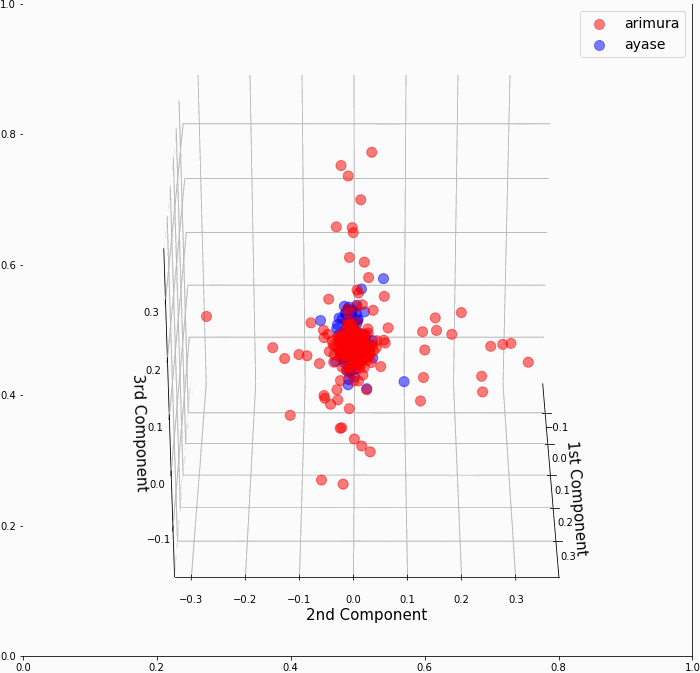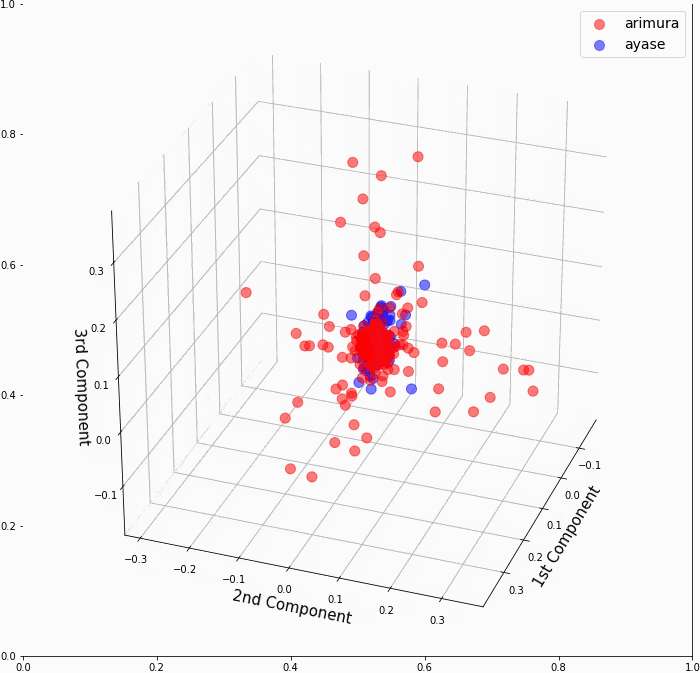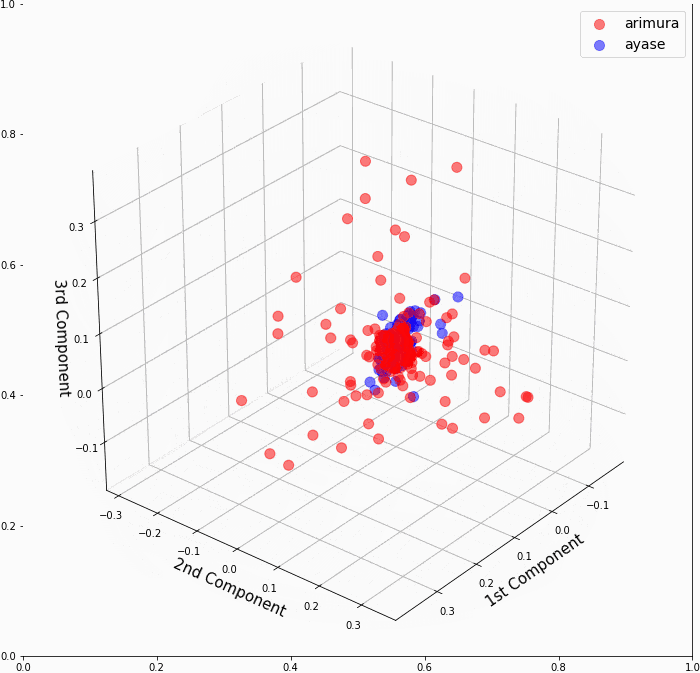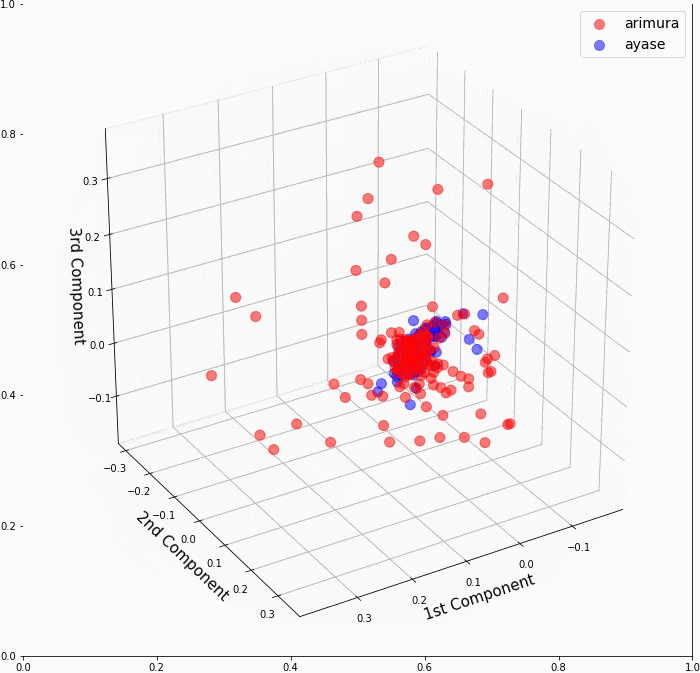
駄目ですね。コアな部分は有村架純と綾瀬はるかが、しっかりとくっ付いていて分離不可でした。

ちなみに、ax.view_init(仰角, 方位角)で、視点を変化させることが出来ます。

全体の流れは、angle=0〜60でグラフ画像を順次作成し、PIL Imageに変換してから 'output.gif' というGIF動画を作成しています。

＊6.3次元グラフの回転では、「3D 散布図を回転 GIF アニメーションにする」のコードを使わさせて頂きました。@hoto17296さん、ありがとうございます。