深層学習／クロスエントロピー

#1.はじめに
　今回は、クロスエントロピー(交差エントロピー)について勉強したことをまとめます。

#2.最尤推定からの導出
　シグモイド関数を $\sigma とし、$y = $\sigma$(W・x + b)とすると、ニューロンが発火(１を出力)する確率は以下の様に表せます。
　　P(C = 1|x) = $\sigma$(W・x + b)

逆に発火しない確率は以下の様に表せます。
　　P(C = 0|x) = 1 - $\sigma$(W・x + b)

この2つを1つの式で表すと、1つのニューロンの発火確率は以下の様に表せます(但し、t=0 or t=1)。
　　P(C = t|x) = $y^t(1 -y)^{1-t}$

ネットワーク全体の尤度Lは、全てのニューロンの発火確率の掛け算になるので、
　　$L = \prod_{n=1}^N y_n^{t_n}(1-y_n)^{1-t_n}$　

　最尤度は、この式を最大化することで求まりますが、最小化する方が最適化しやすいのでマイナスを掛けます。確率の掛け算は、値がどんどん小さくなり扱い難いので、対数(log)を取ります。そして、Nが変化しても比較できる様に、Nで割ると、
　　$L = -\frac{1}{N}\sum_{n=1}^N t_nlogy_n+(1-t_n)log(1-y_n)$

　これが、クロスエントロピー（交差エントロピー）の式です。

#3.具体的な誤差計算
　今、正解ラベル$t_1$〜$t_3$と予測確率$y_1$〜$y_3$が以下の様だとします。

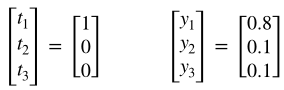
　先程のクロスエントロピーの式に値を代入すると

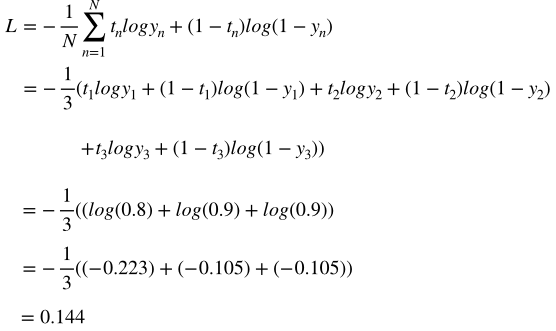
#4.コード
　クロスエントロピーを求めるコードをpythonで書くと、

import numpy as np

def calc_cross_entropy(y_true, y_pred):
    loss = np.mean( -1 * (y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred)), axis=0)
    return loss

y_true =np.array([[1], [0], [0]])
y_pred = np.array([[0.8], [0.1], [0.1]])

answer = calc_cross_entropy(y_true,  y_pred)
print(answer)

# 出力
# [0.14462153]