1.はじめに
transepose の詳しい使い方が良く分からなかったので、調べた結果を備忘録として残します。
2.2次元配列
import numpy as np
img = np.array([[ 0, 1],
[ 2, 3]])
img = img.transpose(1,0)
print(img)
# [[0 2]
# [1 3]]
変換無しが transpose(0, 1)で、軸ナンバーは、**x軸(0), y軸(1)**です。
transpose(1, 0)で、x軸(0)とy軸(1)が入れ替わり、いわゆる転置行列になります。
3.3次元配列
img = np.array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9,10,11],
[12,13,14],
[15,16,17]]])
img = img.transpose(0, 2, 1)
print(img)
# [[[ 0 3 6]
# [ 1 4 7]
# [ 2 5 8]]
# [[ 9 12 15]
# [10 13 16]
# [11 14 17]]]
変換無しが transpose(0, 1, 2) で、軸ナンバーは、**チャンネル軸(0), x軸(1), y軸(2)**です(チャンネル軸は適当に付けた名前です)。x軸, y軸の軸ナンバーは次元数に応じて変化することに注意して下さい。
transpose(0, 2, 1)で、x軸(1)とy軸(2)が入れ替わります。
img = np.array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9,10,11],
[12,13,14],
[15,16,17]]])
img = img.transpose(1, 0, 2)
print(img)
# [[[ 0 1 2]
# [ 9 10 11]]
# [[ 3 4 5]
# [12 13 14]]
# [[ 6 7 8]
# [15 16 17]]]
transpose(1, 0, 2)とx軸(1)をチャネル軸(0)の前に持って来ると、今までは各行列内の処理だったのが、行列間の処理になります。2つの行列の、0行目で1つの行列、1行目で1つの行列、2行目で1つの行列を作ります。
img = np.array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9,10,11],
[12,13,14],
[15,16,17]]])
img = img.transpose(2, 0, 1)
print(img)
# [[[ 0 3 6]
# [ 9 12 15]]
# [[ 1 4 7]
# [10 13 16]]
# [[ 2 5 8]
# [11 14 17]]]
transpose(2, 0, 1)とy軸(2)をチャネル軸(0)の前に持って来ると、先程同様、行列間の処理になります。今度は、2つの行列の0列目で1つの行列、1列目で1つの行列、2列目で1つの行列を作ります。
img = np.array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9,10,11],
[12,13,14],
[15,16,17]]])
img = img.transpose(1, 2, 0)
print(img)
# [[[ 0 9]
# [ 1 10]
# [ 2 11]]
# [[ 3 12]
# [ 4 13]
# [ 5 14]]
# [[ 6 15]
# [ 7 16]
# [ 8 17]]]
さて、transpose(1, 2, 0)とx軸(1), y軸(2)の両方をチャネル軸(0)の前に持って来るとどうなるか。各行列の同じ座標の値を串刺しにしてまとめます。
今回は、x軸(0)が先頭(優先)なので、0行目を串刺しにして1つ行列を作り、1行目を串刺しにして1つの行列を作り、2行目を串刺しにして1つの行列を作ります。
img = np.array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9,10,11],
[12,13,14],
[15,16,17]]])
img = img.transpose(2, 1, 0)
print(img)
# [[[ 0 9]
# [ 3 12]
# [ 6 15]]
# [[ 1 10]
# [ 4 13]
# [ 7 16]]
# [[ 2 11]
# [ 5 14]
# [ 8 17]]]
今度は、transpose(2, 1, 0)とy軸(2)を先頭に持って来ると、y軸(2)が優先になり、0列目を串刺しにして1つ行列を作り、1列目を串刺しにして1つの行列を作り、2列目を串刺しにして1つの行列を作ります。
4次元配列
いよいよ、4次元です。特筆すべき例を一つだけ、説明します。
img = np.array([
[[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9,10,11],
[12,13,14],
[15,16,17]]],
[[[18,19,20],
[21,22,23],
[24,25,26]],
[[27,28,29],
[30,31,32],
[33,34,35]]]
])
img = img.transpose(2, 3, 0, 1)
print(img)
# [[[[ 0 9]
# [18 27]]
# [[ 1 10]
# [19 28]]
# [[ 2 11]
# [20 29]]]
# [[[ 3 12]
# [21 30]]
# [[ 4 13]
# [22 31]]
# [[ 5 14]
# [23 32]]]
# [[[ 6 15]
# [24 33]]
# [[ 7 16]
# [25 34]]
# [[ 8 17]
# [26 35]]]]
変換無しが transpose(0, 1, 2, 3) で、軸ナンバーは、**バッチ軸(0), チャンネル軸(1), x軸(2), y軸(3)**です(バッチ軸, チャンネル軸は適当に名前を付けてます)。
4次元配列で、transpose(2, 3, 0, 1)とやると、各行列の同じ座標を串刺しにするのは3次元配列と同じですが、集計の単位が行ではなく、座標単位となります。そして、座標は、0行0列, 0行1列, 0行2列, 1行0列, ... という順番で行列をまとめます。
transpose(3, 2, 0, 1)の場合は、座標の進む順番が、0行0列, 1行0列, 2行0列, 0行1列, ... に変わるだけで後は同じです。
4.実際の使用例
im2colという畳み込み演算を高速に行うアルゴリズムで、transposeが使われている例を、簡単なサンプルで説明します。
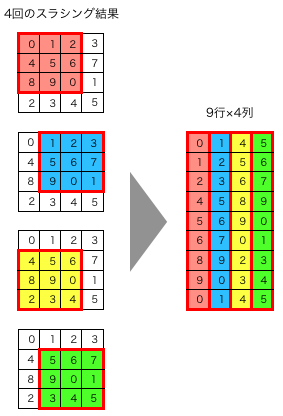
左の4つの行列から右の行列に変換するにはどうしたら良いでしょうか?
img = np.array([
[[[ 0, 1, 2],
[ 4, 5, 6],
[ 8, 9, 0]],
[[ 1, 2, 3],
[ 5, 6, 7],
[ 9, 0, 1]]],
[[[ 4, 5, 6],
[ 8, 9, 0],
[ 2, 3, 4]],
[[ 5, 6, 7],
[ 9, 0, 1],
[ 3, 4, 5]]]
])
print('img.shape = ',img.shape)
img = img.transpose(2, 3, 0, 1)
print(img)
# img.shape = (2, 2, 3, 3)
# [[[[0 1]
# [4 5]]
# [[1 2]
# [5 6]]
# [[2 3]
# [6 7]]]
# [[[4 5]
# [8 9]]
# [[5 6]
# [9 0]]
# [[6 7]
# [0 1]]]
# [[[8 9]
# [2 3]]
# [[9 0]
# [3 4]]
# [[0 1]
# [4 5]]]]
そうなんです。先程のtranspose(2, 3, 0, 1)を使うと、各座標を串刺しにして座標単位でまとめることが出来ます。後は、リシェイプを掛ければ、
img = img.reshape(9, -1)
print(img)
# [[ 0 9 18 27]
# [ 3 12 21 30]
# [ 6 15 24 33]
# [ 1 10 19 28]
# [ 4 13 22 31]
# [ 7 16 25 34]
# [ 2 11 20 29]
# [ 5 14 23 32]
# [ 8 17 26 35]]
出来てしまいました! reshape(9, -1)は、9行だけ決めて後は自動的にリシェイプする形式の書き方(配列がとても大きい時に便利)で、もちろんreshape(9, 4)でもOKです。
結局、先程の処理は、**transpose(2, 3, 0, 1).reshape(9, -1)**とたった1行で表せるわけです。さすが、numpy。