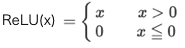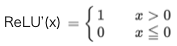深層学習／活性化関数たち

#1.はじめに
　簡単に言うと、ニューラルネットワークの豊かな表現力は、シンプルな活性化関数を入れ子にして深い階層にすることによってもたらされます。

　今回は、ニューラルネットワークで使われる活性化関数について勉強したことをまとめます。

#2.Sigmoid関数

# シグモイド関数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))   

# シグモイド関数の微分
def sigmoid_d(x):
    return (1 / (1 + np.exp(-x))) * ( 1- (1 / (1 + np.exp(-x))))

# グラフ表示
x = np.arange(-5.0, 5.0, 0.01)
plt.plot(x, sigmoid(x), label='sigmoid')
plt.plot(x, sigmoid_d(x), label='sigmoid_d')
plt.ylim(-1.1, 1.1)  
plt.legend()  
plt.grid()
plt.show()

sigmoid関数：

sigmoid(x) = \frac{1}{1+e^{-x}}

sigmoid関数の微分：

sigmoid'(x) = \frac{1}{1+e^{-x}} * ( 1 - \frac{1}{1+e^{-x}})

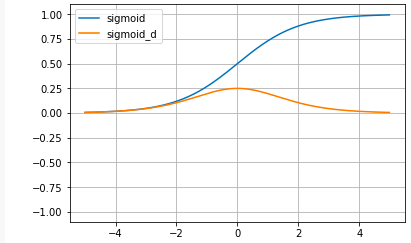
　Sigmoid関数は、昔からニューラルネットワークの教科書には必ず載っていて、微分してもほとんど形が変わらず美しい形をしているのですが、最近は活性化関数としてはほとんど使われていません。　

　その理由は、グラフで分かる様に、xの値が大きくなるとyが1に張り付いて動かなくなってしまうためです。ニューラルネットワークはyを微分して傾きを求めて重みパラメータを最適化するので、微分がほとんど0になってしまうと中々最適解に近づけない(勾配消失)という問題点を持っているからです。

Sigmoid関数の微分の導出

sigmoid'(x) = ((1 + e^{-x})^{-1})'\\

合成関数の微分により、u = 1+e^{-x}と置くと、\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx} なので\\

= -(1 + e^{-x})^{-2} * (1+e^{-x})'\\

= -\frac{1}{(1+e^{-x})^2} * -e^{-x}\\

= \frac{1}{1+e^{-x}} * \frac{e^{-x}}{1+e^{-x}} \\

= \frac{1}{1+e^{-x}} * (\frac{1+e^{-x}}{1+e^{-x}} - \frac{1}{1+e^{-x}})\\

= \frac{1}{1+e^{-x}} * ( 1 - \frac{1}{1+e^{-x}})

#3.tanh関数

# Tanh関数
def tanh(x):
    return (np.exp(x) -np.exp(-x)) / (np.exp(x) + np.exp(-x))

# Tanh関数の微分
def tanh_d(x):
    return 1- ( (np.exp(x) -np.exp(-x)) / (np.exp(x) + np.exp(-x)) )**2

# グラフ表示
x = np.arange(-5.0, 5.0, 0.01)
plt.plot(x, tanh(x), label='tanh')
plt.plot(x, tanh_d(x), label='tanh_d')
plt.ylim(-1.1, 1.1)  
plt.legend()  
plt.grid()
plt.show()

Tanh関数：

tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}}

Tanh関数の微分：

tanh(x) = \frac{4}{(e^x + e^{-x})^2}\\

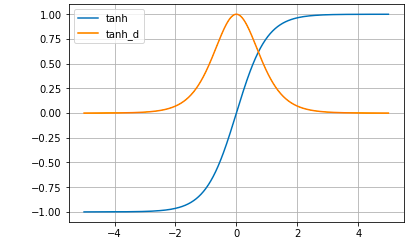
　Tanh関数は、Sigmoid関数の改良版(微分した時の最大値がSigmoidより高い)として使われていたわけですが、xが大きくなるとyが1に貼り付く根本的な問題点は改善されていません。

Tanh関数の微分の導出

商の微分公式　(\frac{f(x)}{g(x)})' = \frac{f'(x)*g(x) - f(x)*g'(x)}{g(x)^2}　を使って\\

tanh'(x) = \frac{(e^x+e^{-x})^2 - (e^x - e^{-x})^2}{(e^x + e^{-x})^2}\\

= \frac{e^{2x}+2+e^{-2x} - (e^{2x} -2 + e^{-2x})}{(e^x + e^{-x})^2}\\

= \frac{4}{(e^x + e^{-x})^2}\\

または、

tanh'(x) = \frac{(e^x+e^{-x})^2 - (e^x - e^{-x})^2}{(e^x + e^{-x})^2}\\

= 1 - \frac{(e^x - e^{-x})^2}{(e^x + e^{-x})^2}\\

= 1 - (\frac{e^x - e^{-x}}{e^x + e^{-x}})^2\\

#4.ReLU関数

# ReLU関数
def relu(x):
    return np.maximum(0, x)

# ReLU関数の微分
def relu_d(x):
    return np.array(x > 0, dtype=np.int)

# グラフ表示
x = np.arange(-5.0, 5.0, 0.01)
plt.plot(x, relu(x), label='relu')
plt.plot(x, relu_d(x), label='relu_d')
plt.ylim(-1.1, 1.1)  
plt.legend()  
plt.grid()
plt.show()

ReLU関数：

ReLU関数の微分：

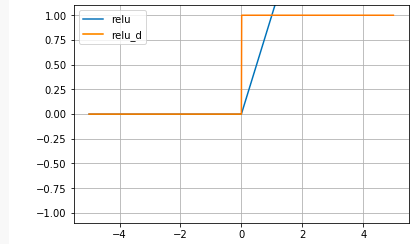
　Sigmoid関数の根本的な問題点をなくすために生まれたのがReLU関数です。xが大きくなってもyも比例して大きくなり常に微分すると定数項が残ります。何か、今聞くと当たり前の様な気がしますが、これが使われ出したのは、なんと2012年頃からです。

　東大の松尾豊先生は、Sigmoid関数はシンプルで微分してもほとんど形が変わらず、理工学者にとって美しい関数だった。一方ReLUはかっこが悪く、しかも(0,0)で微分不可な点があるので、誰も使いたがらなかった。

　昔ディープラーニングは上手く動かせなかったので、皆んな式として美しいSigmoid関数を使っていた。しかし、動かせる様になってからは色々なことを試す人が出て来て、そうした中で使われる様になって来たのがReLUだと言っています。

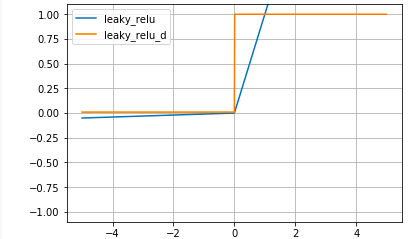
#5.Leaky ReLU関数

# Leaky ReLU関数
def leaky_relu(x):
    return np.where(x > 0, x , 0.01 * x)

# Leaky ReLU関数の微分
def leaky_relu_d(x):
    return np.where(x>0,1,0.01)

# グラフ表示
x = np.arange(-5.0, 5.0, 0.01)
plt.plot(x, leaky_relu(x), label='leaky_relu')
plt.plot(x, leaky_relu_d(x), label='leaky_relu_d')
plt.ylim(-1.1, 1.1)  
plt.legend()  
plt.grid()
plt.show()

Leaky ReLU関数：

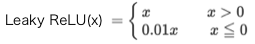
Leaky ReLU関数の微分：

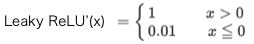
　Leaky ReLU関数は、ReLU関数から派生したもので、xが0以下でも0.01xと傾きを持ちます。ReLU関数より、さらに最適化が進むことが期待されましたが、ReLU関数より最適化が上手く行く場合はかなり限定的な様です。

#6.活性化関数の性能の違いを実感してみる
　最後に、活性化関数によって、どれだけ最適化性能が異なるのか実感してみましょう。

　TensorFlow PlayGround というブラウザでニューラルネットワークのシミュレーションができるサイトを覗いてみます。

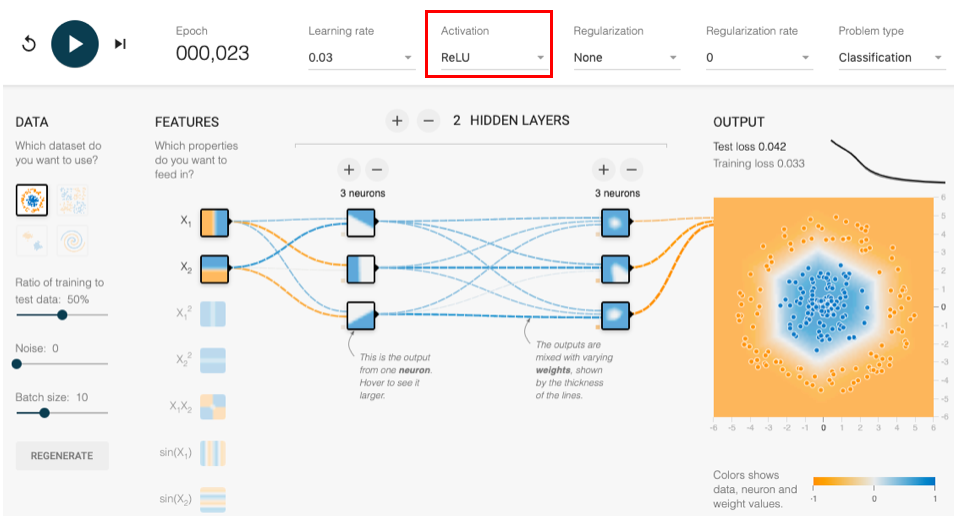
　こんな３個のニューロンが2層のニューラルネットワークを設定し、赤枠のActivation（活性化関数)を切り替えて、収束時間をチェックしてみます。

　確率的な問題もあり、ある程度バラツキは出ますが、収束時間は概ね、TanhがSigmoidの10倍くらい早く、ReLUはTanhのさらに2倍くらい早いです。