機械学習／回帰モデルの性能評価を行ってみる

1.はじめに

　今回は、機械学習に使われる回帰モデルの性能評価を、コードを作りながら行ってみます。

2.データセット

　使用するデータセットは、sklearnに付属しているボストン住宅価格です。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression,Ridge
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor,GradientBoostingRegressor
from sklearn.pipeline import Pipeline
from sklearn.metrics import r2_score
from sklearn.model_selection import cross_val_score
from sklearn.utils import shuffle

# -------- データセットの読み込み ---------
dataset = load_boston()
X = pd.DataFrame(dataset.data, columns=dataset.feature_names)
y = pd.Series(dataset.target, name='y')
print('X.shape = ', X.shape)
print(X.join(y).head())

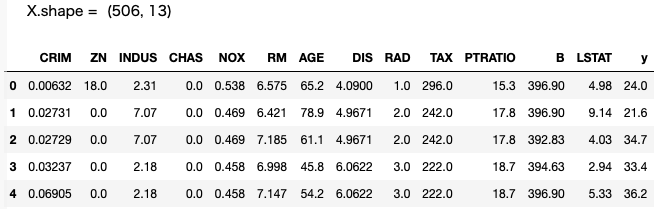
データは全部で506個、特徴量は13項目、yがターゲットとなる住宅価格です。

3.回帰モデル

　今回使用する回帰モデルは5つです。後で、使い易い様に、パイプラインの形でまとめます。ハイパーパラメータは、デフォルトです。

# ---------- パイプラインの設定 -----------
pipelines = {
  '1.Linear': Pipeline([('std',StandardScaler()),
                        ('est',LinearRegression())]),

  '2.Ridge' : Pipeline([('std',StandardScaler()),
                        ('est',Ridge(random_state=0))]),

  '3.Tree'  : Pipeline([('std',StandardScaler()),
                        ('est',DecisionTreeRegressor(random_state=0))]),

  '4.Random': Pipeline([('std',StandardScaler()),
                        ('est',RandomForestRegressor(random_state=0, n_estimators=100))]),  

  '5.GBoost': Pipeline([('std',StandardScaler()),
                        ('est',GradientBoostingRegressor(random_state=0))])
}

1.Linear
　最小二乗法を使った線形回帰モデル(Linear)です。

2.Ridge
　線形回帰モデルに、L2正則化項目を追加して、過学習を抑制したリッジ回帰モデル(Ridge)です。

3.Tree
　決定木(Decision Tree)による回帰モデルです。

4.Random
　ランダムに選んだ特徴量から複数の決定木を作成し、全ての決定木の予測を平均して出力する、ランダムフォレスト（Random Forest)です。

5.GBoost
　既存のツリー群が説明しきれない情報（残差）を後続のツリーが説明しようとする形で、予測精度を高める、勾配ブースティング(Gradient Boosting)です。

4.評価指標

　誤差指標は、R2_scoreを使用します。これは、予測と実測の二乗誤差Σが、実測と実測平均の二乗誤差Σに対してどれだけ小さく出来るかというものです。

　予測が実測と全て一致すれば指標は1、予測があまりにも悪いと指標はマイナスにもなり得ます。

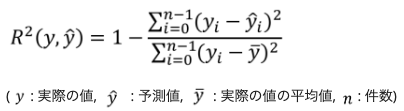
5.ホールドアウト法

　まず、モデルの性能評価をする一般的な方法である、ホールドアウト法を行います。データを 学習データ：テストデータ＝8:2 に分割し、学習データで学習後、未知のテストデータで評価することによって、汎化性能をみるわけです。

# ----------- ホールドアウト法 -----------
X_train,X_test,y_train,y_test = train_test_split(X, y, test_size=0.20, random_state=1)  

scores = {}
for pipe_name, pipeline in pipelines.items():
    pipeline.fit(X_train, y_train)
    scores[(pipe_name,'train')] = r2_score(y_train, pipeline.predict(X_train))
    scores[(pipe_name,'test')] = r2_score(y_test, pipeline.predict(X_test))
print(pd.Series(scores).unstack())

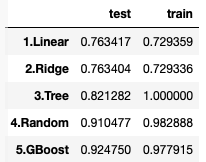
　未知のテストデータで評価した結果、精度が一番高い（0.924750）のは 5.GBoostでした。

　学習データでは、精度の一番高い(1.0000) 3.Tree は、テストデータでは(0.821282)と大きく後退しており、過学習に陥っていることが分かります。

　2.Ridge は 1.Linear の改良版のはずですが、テストデータでは精度が僅かに逆転しています。これはホールドアウト法による精度測定に、ある程度バラツキがあるためで、後でもっと厳密なk-fold法で性能比較を行います。

6.残差プロット

　モデル性能を可視化するために、残差プロットを行います。これは、横軸に予測値、縦軸に予測値と実際値の差を取り、学習データとテストデータをプロットするものです。

# ------------- 残差プロット ------------
for pipe_name, est in pipelines.items():
    y_train_pred = est.predict(X_train)
    y_test_pred = est.predict(X_test)
    plt.scatter(y_train_pred, y_train_pred - y_train, c = 'blue', alpha=0.5, marker = 'o', label = 'train')
    plt.scatter(y_test_pred, y_test_pred - y_test, c = 'red', marker ='x', label= 'test' )
    plt.hlines(y = 0, xmin = 0, xmax = 50, color = 'black')
    plt.ylim([-20, 20])
    plt.xlabel('Predicted values')
    plt.ylabel('Residuals')        
    plt.title(pipe_name)
    plt.legend()
    plt.show()

　コードの出力としては、1.Linear 〜 5.GBoost まで5つの残差プロットされますが、ここでは代表的なものを3つだけ上げます。

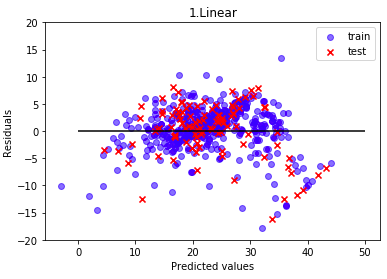
　線形回帰モデルです。学習データ、テストデータとも、ほぼ同じ様な残差のバラツキに成っています。

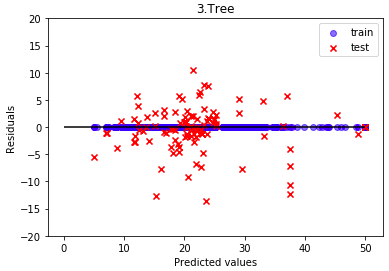
　決定木です。学習データでは完全な残差ゼロ（精度100%)な一方で、テストデータは大きく残差がバラついています。典型的な過学習です。

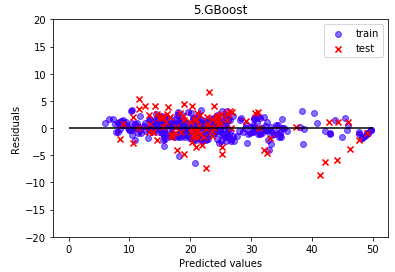
　勾配ブースティングです。学習データ、テストデータとも、残差のバラツキが抑えられています。

7.k-hold法

　ホールドアウト法よりも厳密なモデル評価が出来るのが k-hold法 (k分割交差検証)です。

　具体的な手順は、まずデータをk個に分割し、1つづつ順番に選んでテストデータとし、残りのk-1個を学習データとします。

　そして、学習データで学習を行い、テストデータで精度測定を行うことをk回繰り返し、得られた精度の平均を取りモデルの精度とするのが k-hold法 です。ここでは、k=5で行います(cv = 5 で指定)。

　なお、cross_val_score は、train_test_split の様に、自動でデータをシャッフルしませんので、最初にユーティリティー shuffle を使って、データをシャッフルしてから処理を行います。

# -------------- k-fold法 --------------
X_shuffle, y_shuffle =shuffle(X, y, random_state= 1)  # データシャッフル

scores={}
for pipe_name, est in pipelines.items():  
    cv_results = cross_val_score(est, X_shuffle, y_shuffle, cv=5, scoring='r2')    
    scores[(pipe_name,'avg')] = cv_results.mean()
    scores[(pipe_name,'score')] = np.round(cv_results,5)  # np.roundは桁調整
print(pd.Series(scores).unstack())

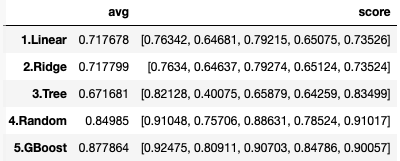
　avgの横にある[ ]に囲まれた5つの数字scoreが、1回毎に算出した精度です。1.Linearを見ると、最低0.64681〜最高0.76342までバラついていることが分かります。この数字を平均することで、厳密なモデル評価を行うわけです。

　2.Ridgeは、1.Linearより僅かですが、精度が向上していることが分かると思います。

　最終的に、ボストン住宅価格において、最も優秀なモデルは、5.GBoost でした。