概要
テーブルデータ用のGANの一つであるCTGANをCensus Incomeデータセットに対して試して偽のテーブルデータを生成します。生成したデータを使ってXGBoostを訓練し、元データと比べてどの程度の精度が出るかを検証します。
CTGAN
GANといえばリアルな偽画像を生成できる技術として有名ですが、非画像データに対するGANの研究も進んでいます。テーブルデータに対応したGANでコードが公開されているものとしては以下のようなものがあります。
- MedGAN [arXiv:1703.06490][GitHub]
- TableGAN [arXiv:1806.03384][GitHub]
- TGAN [arXiv:1811.11264][GitHub]
- CTGAN [arXiv:1907.00503][GitHub]
MedGANは名前の通り医療用データへの応用を念頭に開発されたモデルでカテゴリーデータにのみ対応しています。(同名の医療画像用のモデルも存在します。)
TableGANとTGANは同時期に独立に開発されたモデルで、両者ともカテゴリーデータと数値データ両方を含むテーブルに対応しています。日本語の記事では
でTGANが紹介されています。
今回はTGANのアップデートバージョンであるCTGAN (Conditional Tabular GAN)を試してみます。
CTGANはpipで簡単にインストールできます。
pip install ctgan
データ準備
テーブルデータとしてCensus Incomeと呼ばれるデータセットを使用します。このデータセットは、性別・年齢・学歴や人種などの個人情報から年収が$50,000を超えるかどうかを予測するためのものです。データは上記のリンクからダウンロードできますが、デモ用データとしてCTGANに同梱されていますので、以下のように読み込むことができます。
import numpy as np
import pandas as pd
from ctgan import load_demo
df0 = load_demo()
print(df0.shape)
# (32561, 15)
こうして読み込んだデータには何故かカテゴリー項目の先頭に半角スペースが含まれています。CTGANとXGBoostに流す分には半角スペースが含まれていても問題にならないのですが、データ分析をするときなどに邪魔になるので一応取り除いておきます。
for col in df0.select_dtypes(exclude=np.number).columns:
df0[col] = df0[col].str.replace(' ', '')
最初の数行を表示すると以下のようになっています。
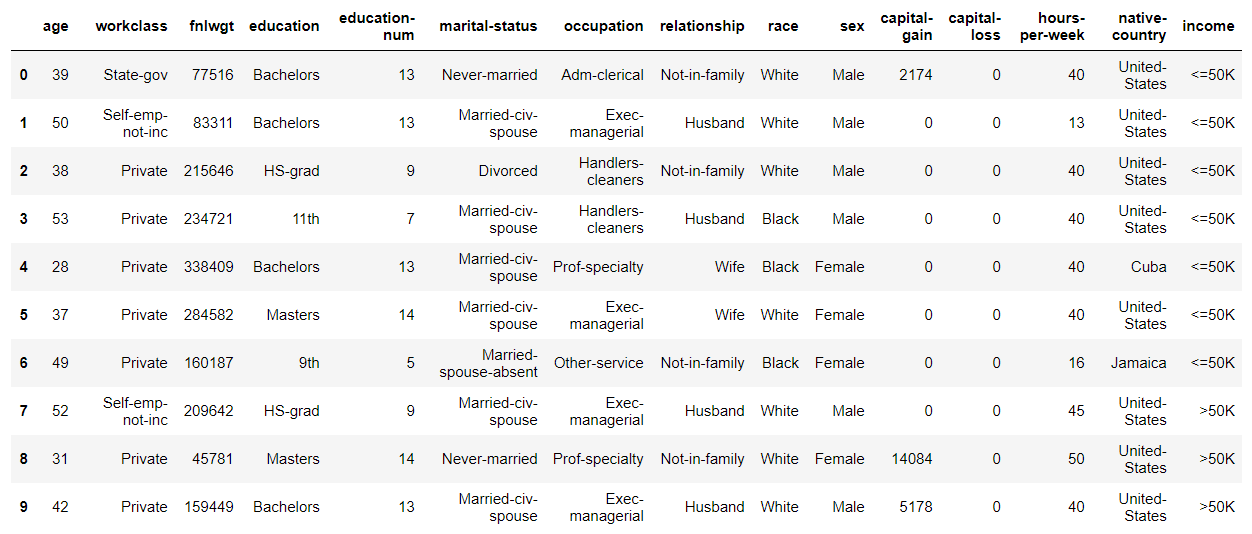
カテゴリー変数のカラムと整数のカラムから成っていることがわかります。
これらのカラムのうち、以下のものは除いてしまうこととします。
'fnlwgt':ID番号のようなものだと思われる
'education-num':'education'と1対1対応している
'capital-gain':ほとんどの行に0が入っている
'capital-loss':同上
df0.drop(['fnlwgt', 'education-num', 'capital-gain', 'capital-loss'],
axis=1, inplace=True)
ちなみにこのデータセットには欠損値は含まれず、もともと欠損値だったと思われる箇所には'?'が入っています。今回は'?'はそのままにして処理を続けます。
次に、データセットを訓練用とテスト用に分けます。訓練用データはCTGANの訓練とXGBoostの訓練の両方に使います。
df0_train, df_test = train_test_split(df0,
test_size=0.2,
random_state=0,
stratify=df0['income'])
print(len(df0_train)) # 26048
print(len(df_test)) # 6513
訓練用データはもう一つサイズの小さなものも準備しておきます。
df1_train, _ = train_test_split(df0_train,
test_size=0.9,
random_state=0,
stratify=df0_train['income'])
print(len(df1_train)) # 2604
データ生成
まず、サイズの大きいほうの訓練データdf0_trainを使って、CTGANを学習させてみましょう。学習させる際には、カテゴリー変数のカラム名を指定してやる必要があります。
discrete_columns = [
'workclass',
'education',
'marital-status',
'occupation',
'relationship',
'race',
'sex',
'native-country',
'income'
]
学習は以下のように簡単に実行できます。入力データはpandas.DataFrameとnumpy.ndarrayに対応しています。
from ctgan import CTGANSynthesizer
ctgan0 = CTGANSynthesizer()
ctgan0.fit(df0_train, discrete_columns)
学習はデフォルトの設定だと300epoch実行されます。
学習が終了したらデータを生成します。生成されるデータは入力データと同じ形式となるので、今の場合はpandas.DataFrameが返されます。生成するデータのサンプル数(行数)は自由に設定できます。いくら作ってもタダですので、思い切って100万行作ってみましょう。
n_samples = 1000000
df0_syn = ctgan0.sample(n_samples)
print(df0_syn.shape)
# (1000000, 11)
生成したデータの最初の数行は以下のようになっています。
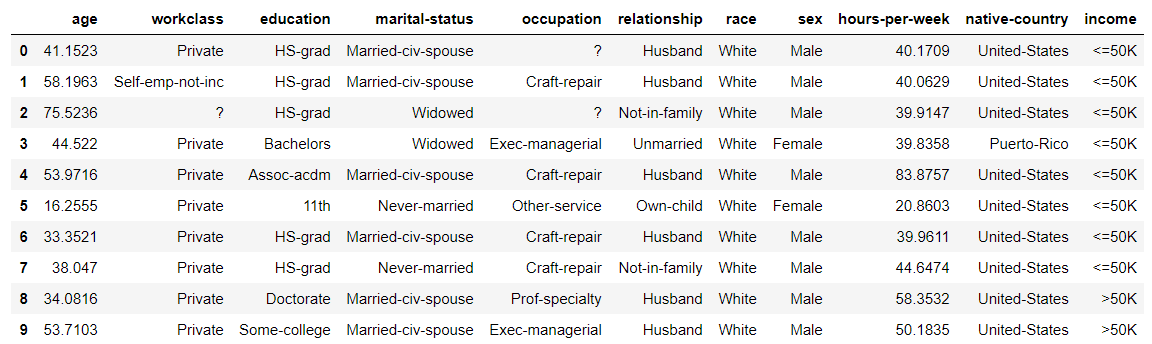
数値データはもともと整数であっても浮動小数点とみなされてデータが作られてしまいますので、生成後に自分で整数に変換してやる必要があります。
for col in ['age', 'hours-per-week']:
df0_syn[col] = df0_syn[col].astype(int)
さて、CTGANの旧バージョンのTGANの原論文ではデータ項目間の相関を計算して生成データがどれほど元データに似ているかを調べていましたが、ここでは単純にターゲット項目である'income'の分布を元データと生成データで比べてみましょう。
print("original data")
print(df0_train['income'].value_counts(normalize=True))
# <=50K 0.759175
# >50K 0.240825
print("synthetic data")
print(df0_syn['income'].value_counts(normalize=True))
# <=50K 0.822426
# >50K 0.177574
もともと50K超の割合が少ない非均一データでしたが、生成データでは50K超の割合がさらに少なくなってしまっています。元データの分布がそれほど正確には学習されていないということでしょうか。ともかくXGBoostを学習させることで生成データの品質を調べてみましょう。
XGBoost学習①
生成データを使ってXGBoostを学習させ、元データを使った場合と比較することで、生成データが元データにどれだけ似ているのかを評価してみます。さらに、生成データを元データに混ぜて学習させることで、元データだけの場合よりモデルの精度を上げることができるかを試してみます。
まず、データ前処理を行います。今回は単純にカテゴリー変数を数値に変換する(ラベルエンコード)だけにします。
分割した後のdf_testなどの小さなデータフレーム中には現れない稀な変数が存在する可能性もありますので、まず元のデータフレームdf0を用いて各カテゴリー変数のリストを収めた辞書を作成し、それをscikit-learnのLabelEncoderを用いて各データフレームに適用します。
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
category_dict = {}
for col in discrete_columns:
category_dict[col] = df0[col].unique()
def preprocessing(df, category_dict):
df_ = df.copy()
for k, v in category_dict.items():
le.fit(v)
df_[k] = le.transform(df_[k])
y = df_['income']
X = df_.drop('income', axis=1)
return X, y
上記で作成した関数を各データフレームに適用します。
X0_train, y0_train = preprocessing(df0_train, category_dict)
print(X0_train.shape, y0_train.shape)
# (26048, 10) (26048,)
X_test, y_test = preprocessing(df_test, category_dict)
print(X_test.shape, y_test.shape)
# (6513, 10) (6513,)
X0_syn, y0_syn = preprocessing(df0_syn, category_dict)
print(X0_syn.shape, y0_syn.shape)
# (1000000, 10) (1000000,)
XGBoostを訓練してテストデータに対する精度評価を出力する関数を用意します。XGBoostのハイパーパラメータは全データdf0を用いてグリッドサーチで決定したものです。
def learn_predict(X, y, X_test, y_test):
xgb = XGBClassifier(learning_rate=0.1, max_depth=7, min_child_weight=4)
xgb.fit(X, y)
predictions = xgb.predict_proba(X_test)
auc = roc_auc_score(y_test, predictions[:, 1])
bool_pediction = (predictions[:, 1] >= 0.5).astype(int)
acc = accuracy_score(y_test, bool_pediction)
precision = precision_score(y_test, bool_pediction)
recall = recall_score(y_test, bool_pediction)
f1 = f1_score(y_test, bool_pediction)
print("AUC: {:.3f}".format(auc))
print("Accuracy {:.3f}".format(acc))
print("Precision: {:.3f}".format(precision))
print("Recall: {:.3f}".format(recall))
print("f1: {:.3f}".format(f1))
print("Confusion matrix:")
print(confusion_matrix(y_test, bool_pediction))
return (auc, acc, precision, recall, f1)
Precision, Recall, f1については収入が50K超というターゲットに対するものです。
まず、元の訓練データ(26,048件)で学習した場合の結果を見てみましょう。精度評価は常に最初に分割した元のテストデータ(6,513件)を用います。
ac0 = learn_predict(X0_train, y0_train, X_test, y_test)
# AUC: 0.888
# Accuracy: 0.838
# Precision: 0.699
# Recall 0.578
# f1: 0.632
# Confusion matrix:
# [[4554 391]
# [ 662 906]]
こちらの結果をベースラインとして生成データを用いた結果と比較していきます。
生成データを用いるときにはサンプルの数を変えて学習を行い、サンプル数によって精度がどのように変わるかを見てみます。
n_samples = [1000, 3000, 10000, 30000, 100000, 300000, 1000000]
auc_list0 = []
acc_list0 = []
precision_list0 = []
recall_list0 = []
f1_list0 = []
for n in n_samples:
print("==" * 12)
print(" # of samples: ", n)
print("==" * 12)
ac = learn_predict(X0_syn[:n], y0_syn[:n], X_test, y_test)
print()
auc_list0.append(ac[0])
acc_list0.append(ac[1])
precision_list0.append(ac[2])
recall_list0.append(ac[3])
f1_list0.append(ac[4])
結果を表にすると以下のようになります。
| # of samples | 1K | 3K | 10K | 30K | 100K | 300K | 1M | Original |
|---|---|---|---|---|---|---|---|---|
| AUC | 0.825 | 0.858 | 0.857 | 0.868 | 0.873 | 0.875 | 0.876 | 0.888 |
| Accuracy | 0.795 | 0.816 | 0.816 | 0.822 | 0.821 | 0.823 | 0.822 | 0.838 |
| Precision | 0.650 | 0.682 | 0.703 | 0.729 | 0.720 | 0.723 | 0.717 | 0.699 |
| Recall | 0.327 | 0.440 | 0.407 | 0.417 | 0.423 | 0.430 | 0.429 | 0.578 |
| f1 | 0.435 | 0.539 | 0.515 | 0.531 | 0.533 | 0.540 | 0.537 | 0.632 |
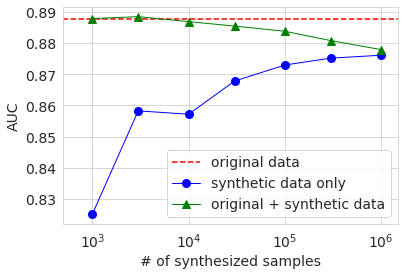
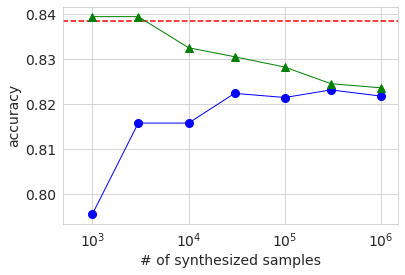
振る舞いは完全に単調ではないものの、どの精度指標でもサンプル数を増やすほど精度が上昇する傾向があります。ただし、precision以外では最大サンプル数の結果でも元データの値よりも低くなっています。精度評価は元データから分割したテストデータで行っていますので、この結果は生成データの分布は元データと完全には一致していないということを示唆しています。precisionに限っては生成データのサンプル数が大きい場合のほうが元データの場合より精度が良いですが、これは生成データでは50K超のサンプル数の割合が元データよりも小さいことが関係しているのではないかと思います。
AUC, Accuracy, f1の結果をグラフにすると下図のようになります。横軸は生成データのサンプル数を対数で示したものです。赤い点線がベースラインの元データの結果で、青い丸が生成データの結果です。緑の三角については後述します。これらのグラフを見ても、生成データのサンプル数を増やすと精度は上がる傾向があるが、ある程度で頭打ちし、元データの結果には及ばないということが見て取れます。
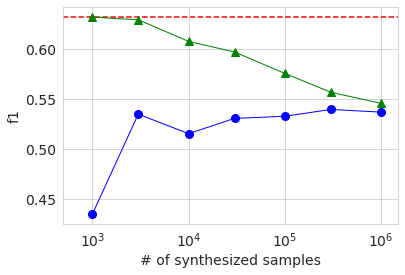
次に、元データに生成データを混ぜ合わせて学習させてみます。今回も生成データの数を変化させています。
n_samples = [1000, 3000, 10000, 30000, 100000, 300000, 1000000]
auc_list0a = []
acc_list0a = []
precision_list0a = []
recall_list0a = []
f1_list0a = []
for n in n_samples:
X = pd.concat([X0_train, X0_syn[:n]])
y = pd.concat([y0_train, y0_syn[:n]])
print("==" * 12)
print(" # of samples: ", n)
print("==" * 12)
ac = learn_predict(X, y, X_test, y_test)
print()
auc_list0a.append(ac[0])
acc_list0a.append(ac[1])
precision_list0a.append(ac[2])
recall_list0a.append(ac[3])
f1_list0a.append(ac[4])
こちらの結果は上のグラフに緑の三角で示してあります。
生成データのサンプル数が元データの数と同程度の数千のときは、各種精度は元データのみのベースラインと同程度か少し上回っています。ただし、上回っているといっても違いはごくわずかであり、この実験からは有意な違いかどうかは判別できません。生成データのサンプル数を増やすと、データ中の元データの割合が減少しますので、精度は下がってしまい、生成データのみで学習した場合の精度に漸近する様子が見て取れます。
XGBoost学習②
さて、実務的な場面で偽データを使ってデータの水増しをしたくなるのは、学習に使えるデータの数が少ないときだと思います。そのような場面を想定して、最初に準備したサイズの小さな訓練データdf1_trainを使用して同じ計算を行ってみます。df1_trainの行数はdf0_trainの1/10の2604です。
コードは先ほどと同様なので割愛しますが、CTGANを訓練し、100万行のデータdf1_synを生成、XGBoostの訓練を行いました。
まず、ベースラインの元データ2604件のみを用いた学習の結果は以下の通りです。
ac1 = learn_predict(X1_train, y1_train, X_test, y_test)
# AUC: 0.867
# Accuracy: 0.821
# Precision: 0.659
# Recall 0.534
# f1: 0.590
# [[4512 433]
# [ 730 838]]
やはりデータ数を減らした分、全体的に精度は低化しています。
次に、生成データを使った学習の結果を先ほどと同様のグラフにして示します。
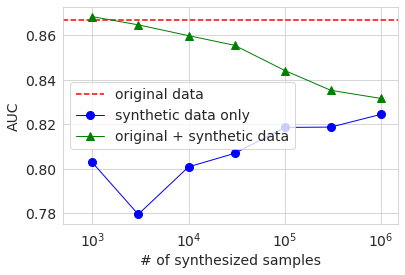
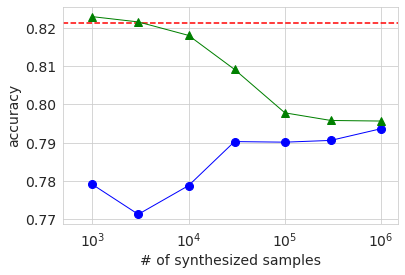
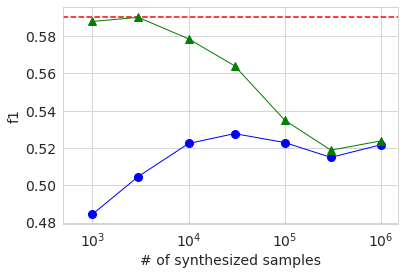
全体的な振る舞いの傾向は大きなデータセットを使った場合と同じになっています。生成データのみを使った場合(青丸)のAUCとAccuracyがサンプル数3000の時のほうが1000の時より低いのは、元データが少ないために生成データの品質のばらつきが大きくなったためではないかと推察します。いずれにせよ、先ほど同様に生成データを付け加えて学習しても元データのみの場合より有意に精度が上がることはありませんでした。
おわりに
GANを使ってデータを水増ししてモデルの精度を上げられないかと期待したのですが、今回の実験ではうまく行きませんでした。ただし、生成データのみを使った結果も元データのみの場合と比べてそれほど大きく劣るわけではないので、プライバシーや情報セキュリティの問題で元データを自由に取り扱えない場合に、偽データを生成して代わりに使うなどの活用法はあるかもしれません。