ソートアルゴリズム

はじめに

ソートとは？とよく使われるソートの挙動を書いていこうと思います

ソートとは？

入力として与えられた数字を小さい順に並べること
日本語では「整列」

example.

numbers = [3,5,7,6,39,1]
ソートすると
numbers = [1,3,5,6,7,39]

バブルソート

数列の中を右から左に向かって隣合う２つの数字を比較し、右の値のほうが小さければ入れ替える。

example.

numbers = [4,8,2,6]

1:2と6を比較、6のほうが大きいから変更なしで次の比較に進む
2:8と2を比較、2ほうが小さいから入れ替える
numbers = [4,2,8,6]
3:４と2を比較、2のほうが小さいから入れ替える
numbers = [2,4,8,6]
左端まで進めば第一ラウンドが終了し、次のラウンドに進む

この操作を繰り返すことで最終的にはソートされた数列が還る

入力データが小さい順に並んでいれば入れ替えは一回も発生せず、逆に入力データが大きい順に並んでいれば毎回比較後に入れ替えをすることになる

選択ソート

数列の中から最小値を検索し、左端の数字と入れ替える

example.

numbers = [4,8,2,6]

1:数列を線形探索し、最小値2を左端の4と交換する（第一ラウンド）
numbers = [2,8,4,6]
2:残る数列を再び線形探索し、最小値4と左端の8を交換する(第二ラウンド)
numbers = [2,4,6,8]

この操作を繰り返すことで最終的にはソートされた数列が還る

数字の入れ替えは各ラウンドで一回となる

挿入ソート

数列の左側から順番にソートしていく
右側の未探索領域から数字を一つとってきてソート済みの領域の適正な場所に挿入する

example.

numbers = [4,8,2,6]

1:左端の4をソート済みにする
2:未探索領域の左端である8を取り出し、ソート済みの4と比較する
3:8>4だから４の右に配置する
numbers = [4,8,2,6]
4:次に比較する2は8>4>2だから2を左端に配置する
numbers = [2,4,8,6]

この操作を繰り返すことで最終的にはソートされた数列が還る

入力データが大きい順に並んでいる場合は比較数が多くなってしまう

ヒープソート

データ構造のヒープを利用することが特徴

参照サイト

1:入力された数列を降順になるようヒープとして構築する
２：値の大きい順に取り出してソートする
3:ヒープを再構築する

この操作を繰り返すことで最終的にはソートされた数列が還る

バブルソート・選択ソート・挿入ソートに比べて高速だが、ヒープという複雑なデータ構造を利用するため実装が複雑になる

マージソート

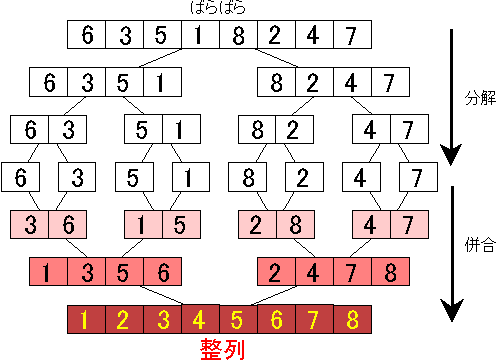
数列をほぼ同じ長さの2つの数列に分割していき、これ以上分割できなくなったところからグループ同士をマージしていく

参考サイト

図の通り各グループの数が1つになれば、隣りあう数をソートしながらマージしていく
この操作を繰り返すことで最終的にはソートされた数列が還る

マージソートにおいて数字を分割していく部分に計算時間はかからない
２つのソート済み数列をマージする部分は先頭の数を比較して小さい方を配置していくような処理

クイックソート

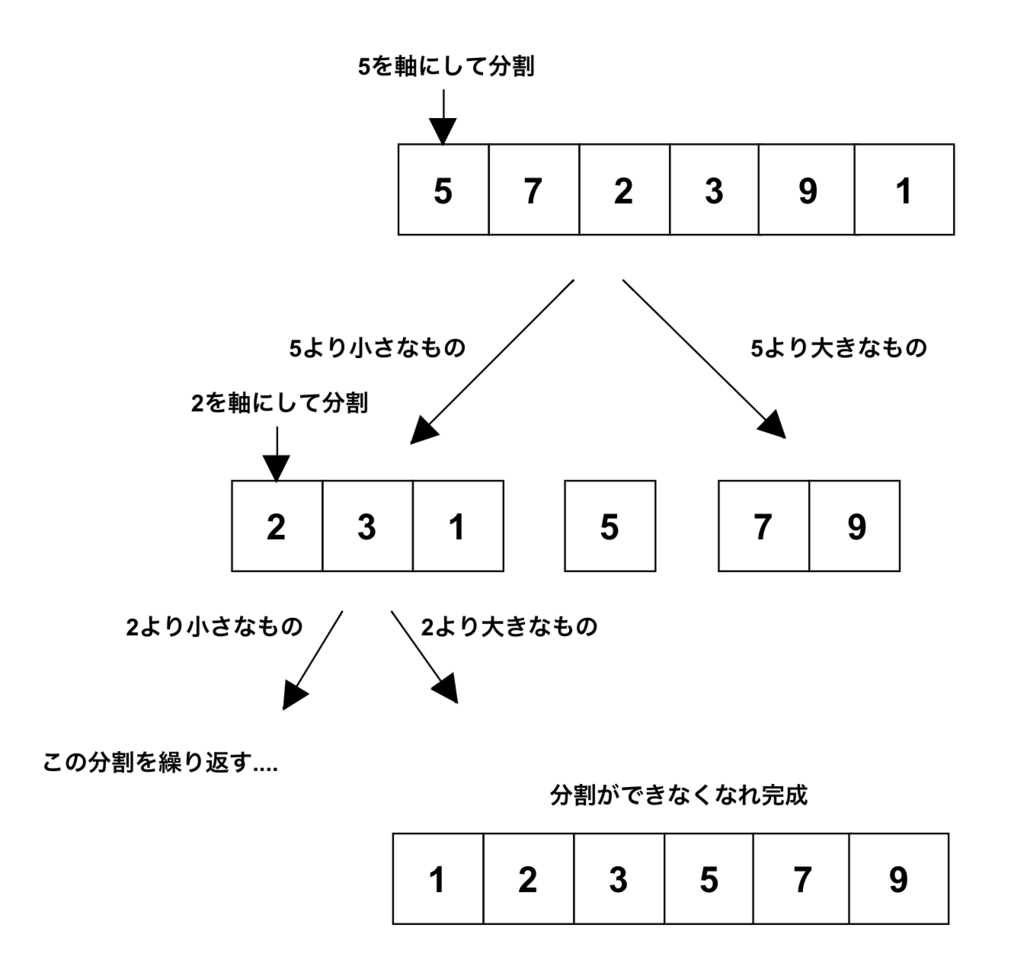
基準となる数（ピボット）を数列の中からランダムに一つ選び、ピボット以外の数を「ピボットより小さい数」と「ピボット以上の数」の２つのグループに分ける

example.

numbers = [4,8,2,6,5,1]
1:ピボットを6とする
2:左端の4は4<6なので左側に配置する
3:8は8>6なので右側に配置する
4:繰り返すと「6より少ない数」、「6以上の数」に二分される
numbers = [[4,2,5,1],6,[8]]
5:グループ化した数列を1~4の操作にようにソートする

[参考サイト](https://to-bb.hatenablog.com/entry/2018/04/20/080000) この操作を繰り返すことで最終的にはソートされた数列が還る

元の数列を二つの子問題（ピボットより小さい数、ピボット以上の数）に分割し、その子問題にもピボットを設定してソートしていく
このようにアルゴリズムの内部にそのアルゴリズム自身を使うことを「再帰」という

参考図書

アルゴリズム図鑑