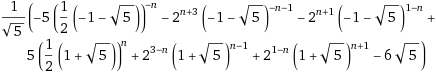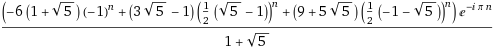ググっても見当たらなかったので。

背景

NHKから国民を守る党のツイートを見て、「NHKから国民を守る党からNHKを守る党」というオヤジギャグが浮かんだ。この党はおそらく「NHKから国民を守る党」によるNHKへの抗議活動からNHKを守ることを掲げるのだろう。

さらに、その党に対抗して「NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党」という党も考えられることに気づいた。この党はおそらく「NHKから国民を守る党からNHKを守る党」による「NHKから国民を守る党」への抗議活動から「NHKから国民を守る党」を守ることを掲げるのだろう。

さらに、その党に対抗して「NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党からNHKから国民を守る党からNHKを守る党を守る党」という党も考えられることに気づいた。この党はおそらく「NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党」による「NHKから国民を守る党からNHKを守る党」への抗議活動から「NHKから国民を守る党からNHKを守る党」を守ることを掲げるのだろう。

さらに、その党に対抗して「NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党からNHKから国民を守る党からNHKを守る党を守る党からNHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党を守る党」という党も考えられることに気づいた。

以下無限に続く。

なお、この記事には政治の話題は特に出てきません。

NHKから国民を守る党系列の一般化

NHKから国民を守る党に始まり、それに対抗する党のチェーンで表される系列（以下、NHKから国民を守る党系列と省略）を最初から並べてみる。

NHKから国民を守る党
NHKから国民を守る党からNHKを守る党
NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党
NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党からNHKから国民を守る党からNHKを守る党を守る党
NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党からNHKから国民を守る党からNHKを守る党を守る党からNHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党を守る党

これを見ると、すべてのNHKから国民を守る党系列は「≪迎撃対象≫から≪防衛対象≫を守る党」という形を成していることが分かる。

表

これを表にすると次のようになる。

政党名	迎撃対象	防衛対象
NHKから国民を守る党	NHK	国民
NHKから国民を守る党からNHKを守る党	NHKから国民を守る党	NHK
NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党	NHKから国民を守る党からNHKを守る党	NHKから国民を守る党
NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党からNHKから国民を守る党からNHKを守る党を守る党	NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党	NHKから国民を守る党からNHKを守る党
NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党からNHKから国民を守る党からNHKを守る党を守る党からNHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党を守る党	NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党からNHKから国民を守る党からNHKを守る党を守る党	NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党

この通り、斜めに同じ政党名が並んでいるのが分かる。

漸化式

そこで、NHKから国民を守る党系列を漸化式で表現することを考える。

$N(0)=国民$
$N(1)=NHK$

とおくと、

$N(2)=NHKから国民を守る党=N(1)からN(0)を守る党$
$N(3)=NHKから国民を守る党からNHKを守る党=N(2)からN(1)を守る党$
$N(n)=N(n-1)からN(n-2)を守る党$

となる。

冒頭のアレの短縮

せっかく関数化したので、冒頭のアレを短縮してみよう。

$N(2)$のツイートを見て、$N(3)$というオヤジギャグが浮かんだ。
この党はおそらく$N(2)$による$N(1)$への抗議活動から$N(1)$を守ることを掲げるのだろう。
さらに、その党に対抗して$N(4)$という党も考えられることに気づいた。
この党はおそらく$N(3)$による$N(2)$への抗議活動から$N(2)$を守ることを掲げるのだろう。
さらに、その党に対抗して$N(5)$という党も考えられることに気づいた。
この党はおそらく$N(4)$による$N(3)$への抗議活動から$N(3)$を守ることを掲げるのだろう。
さらに、その党に対抗して$N(6)$という党も考えられることに気づいた。

更に無限に続けるとこうなる。

$N(2)$のツイートを見て、$N(3)$というオヤジギャグが浮かんだ。
この党はおそらく$N(2)$による$N(1)$への抗議活動から$N(1)$を守ることを掲げるのだろう。
for (n = 4; ; n++) {
　さらに、その党に対抗して$N(n)$という党も考えられることに気づいた。
　この党はおそらく$N(n-1)$による$N(n-2)$への抗議活動から$N(n-2)$を守ることを掲げるのだろう。
}

プログラム化

上記の$n$を与えると$N(n)$を返すプログラムをPerlで記述してみた。

sub N {
  my $n = shift;
  return $n == 0 ? "国民"
       : $n == 1 ? "NHK"
       :           N($n - 1)."から".N($n - 2)."を守る党";
}
print N(4), "\n";

同等なプログラムのワンライナーバージョン

$ perl -E 'sub N { my $n = shift; $n == 0 ? "国民" : $n == 1 ? "NHK" : N($n - 1)."から".N($n - 2)."を守る党" } say N $ARGV[0]' 0
国民

$ perl -E 'sub N { my $n = shift; $n == 0 ? "国民" : $n == 1 ? "NHK" : N($n - 1)."から".N($n - 2)."を守る党" } say N $ARGV[0]' 1
NHK

$ perl -E 'sub N { my $n = shift; $n == 0 ? "国民" : $n == 1 ? "NHK" : N($n - 1)."から".N($n - 2)."を守る党" } say N $ARGV[0]' 2
NHKから国民を守る党

$ perl -E 'sub N { my $n = shift; $n == 0 ? "国民" : $n == 1 ? "NHK" : N($n - 1)."から".N($n - 2)."を守る党" } say N $ARGV[0]' 3
NHKから国民を守る党からNHKを守る党

$ perl -E 'sub N { my $n = shift; $n == 0 ? "国民" : $n == 1 ? "NHK" : N($n - 1)."から".N($n - 2)."を守る党" } say N $ARGV[0]' 4
NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党

これで、NHKを一次創作、「NHKから国民を守る党」を二次創作とした場合の十四次創作なども簡単に出力できるようになった。

奇妙な縞模様が美しい。この縞模様には一体どのような規則性があるのだろうか？セルオートマトンなどで記述することはできないだろうか？など、興味は絶えない。

括弧を入れてみる

Twitterの人のアイデアで、＜［NHK］から［国民］を守る党＞から＜NHK＞を守る党のように階層ごとに括弧でくくるようにしてみた。

$ perl -E '@a = qw/（ ｛ ［ ＜ 【 〈 『 《 〔 〖/; @b = qw/） ｝ ］ ＞ 】 〉 』 》 〕 〗/; sub N { my $n = shift; my $k = $n % 10; $n == 0 ? "国民" : $n == 1 ? "NHK" : $a[$k].N($n - 1)."$b[$k]から$a[$k]".N($n - 2)."$b[$k]を守る党" } say N $ARGV[0]' 0
国民

$ perl -E '@a = qw/（ ｛ ［ ＜ 【 〈 『 《 〔 〖/; @b = qw/） ｝ ］ ＞ 】 〉 』 》 〕 〗/; sub N { my $n = shift; my $k = $n % 10; $n == 0 ? "国民" : $n == 1 ? "NHK" : $a[$k].N($n - 1)."$b[$k]から$a[$k]".N($n - 2)."$b[$k]を守る党" } say N $ARGV[0]' 1
NHK

$ perl -E '@a = qw/（ ｛ ［ ＜ 【 〈 『 《 〔 〖/; @b = qw/） ｝ ］ ＞ 】 〉 』 》 〕 〗/; sub N { my $n = shift; my $k = $n % 10; $n == 0 ? "国民" : $n == 1 ? "NHK" : $a[$k].N($n - 1)."$b[$k]から$a[$k]".N($n - 2)."$b[$k]を守る党" } say N $ARGV[0]' 2
［NHK］から［国民］を守る党

$ perl -E '@a = qw/（ ｛ ［ ＜ 【 〈 『 《 〔 〖/; @b = qw/） ｝ ］ ＞ 】 〉 』 》 〕 〗/; sub N { my $n = shift; my $k = $n % 10; $n == 0 ? "国民" : $n == 1 ? "NHK" : $a[$k].N($n - 1)."$b[$k]から$a[$k]".N($n - 2)."$b[$k]を守る党" } say N $ARGV[0]' 3
＜［NHK］から［国民］を守る党＞から＜NHK＞を守る党

$ perl -E '@a = qw/（ ｛ ［ ＜ 【 〈 『 《 〔 〖/; @b = qw/） ｝ ］ ＞ 】 〉 』 》 〕 〗/; sub N { my $n = shift; my $k = $n % 10; $n == 0 ? "国民" : $n == 1 ? "NHK" : $a[$k].N($n - 1)."$b[$k]から$a[$k]".N($n - 2)."$b[$k]を守る党" } say N $ARGV[0]' 4
【＜［NHK］から［国民］を守る党＞から＜NHK＞を守る党】から【［NHK］から［国民］を守る党】を守る党

$ perl -E '@a = qw/（ ｛ ［ ＜ 【 〈 『 《 〔 〖/; @b = qw/） ｝ ］ ＞ 】 〉 』 》 〕 〗/; sub N { my $n = shift; my $k = $n % 10; $n == 0 ? "国民" : $n == 1 ? "NHK" : $a[$k].N($n - 1)."$b[$k]から$a[$k]".N($n - 2)."$b[$k]を守る党" } say N $ARGV[0]' 7
《『〈【＜［NHK］から［国民］を守る党＞から＜NHK＞を守る党】から【［NHK］から［国民］を守る党】を守る党〉から〈＜［NHK］ から［国民］を守る党＞から＜NHK＞を守る党〉を守る党』から『【＜［NHK］から［国民］を守る党＞から＜NHK＞を守る党】から【［NHK］から［国民］を守る党】を守る党』を守る党》から《〈【＜［NHK］から［国民］を守る党＞から＜NHK＞を守る党】から【［NHK ］から［国民］を守る党】を守る党〉から〈＜［NHK］から［国民］を守る党＞から＜NHK＞を守る党〉を守る党》を守る党

結果、特に見やすくはならないことが判明した。

開幕には$n-1$回の括弧があり、末尾には約$n/2$回のを守る党があることが面白い。

末尾のトークンの反復数について

なぜ開幕の反復部分は概ね$n$の速さで増えるのに、末尾の反復部分は$n/2$の速さになるのだろうか。

それには一般項の最も端に位置する関数呼び出しの引数が関わってくる。括弧つきの$N(n)$を

$M(n)=「M(n-1)」から「M(n-2)」を守る党$

と記述したとき、冒頭部分は、$M(n-1)$によって1個前の括弧の数を参照し、さらにそこに括弧を1個付け足すため、括弧の個数を1増やすのに$n$が1かかる。

しかし末尾部分は$M(n-2)$によって2個前の反復数を参照し、そこに1個だけ反復数を加えるため、反復数が1増えるのに$n$が2かかる。末尾の反復数は$N(0)$および$N(1)$のときに0で、以降$n$が偶数のときに1ずつ増加する。

NHKから国民を守る党数列

$n$に対応するNHKから国民を守る党系列の文字数$len(N(n))$（以下、NHKから国民を守る党数列と省略）について考えてみる。

まず、漸化式は以下のようになる。

$len(N(0))=len(国民)=2$
$len(N(1))=len(NHK)=3$
$len(N(n))=len(N(n-1)からN(n-2)を守る党)$
　　　　　　$=len(N(n-1))+2+len(N(n-2))+4$
　　　　　　$=len(N(n-1))+len(N(n-2))+6$

これに対応するプログラムは次のようになる。

$ perl -E 'sub N { my $n = shift; $n == 0 ? 2 : $n == 1 ? 3 : N($n - 1) + N($n - 2) + 6 } say N $ARGV[0]' 7
175

$n$が0から14までのときのNHKから国民を守る党数列を表にするとこうなる。

$n$	NHKから国民を守る党数列
0	2
1	3
2	11
3	20
4	37
5	63
6	106
7	175
8	287
9	468
10	761
11	1235
12	2002
13	3243
14	5251

フィボナッチ数の和の形にしてみる

この数列はフィボナッチ数列となんらかの関係がありそうに見える。

そこでWolfram Alphaに入れてみた所、$len(N(n))=5F_n+4L_n-6$という結果が得られた。

$F_n$は$n$番目のフィボナッチ数で、$L_n$は$n$番目のリュカ数である。

フィボナッチ数とは、「最初が0, 1で、以降1個前と2個前の値を足した数列」であるが、リュカ数は「最初が2, 1で、以降1個前と2個前の値を足した数列」であり、$L_n=F_{n-1}+F_{n+1}$のような関係式が知られている。

そのため、NHKから国民を守る党数列は次のようにフィボナッチ数列の和の形で表せる。

$len(N(n))=4F_{n-1}+5F_n+4F_{n+1}-6$

比

隣り合うフィボナッチ数の比は黄金比$\frac{1+\sqrt{5}}{2}≒1.6180339887$に収束する。NHKから国民を守る党数列はフィボナッチ数と定数項からなるため、最終的には黄金比に収束する。

実際、十分大きな数を与えてみるとそれっぽい比が得られる。

$n$	NHKから国民を守る党数列
30	11602186
31	18772735

$len(N(31))/len(N(30))=18772735/11602186≒1.61803430836$

一般項

フィボナッチ数列には一般項の式が知られているので、展開していくとなんだかんだで$len(N(n))=$((-6*(1+√5)*(-1)^n+(3*√5-1)*(1/2*(√5-1))^n+(9+5*√5)*(1/2(-1-√5))^n)*e^(-i*π*n))/(1+√5)という式ができる。

https://www.wolframalpha.com/input/?i=x%3D%28%28-6*%281%2B%E2%88%9A5%29*%28-1%29%5En%2B%283*%E2%88%9A5-1%29*%281%2F2*%28%E2%88%9A5-1%29%29%5En%2B%289%2B5*%E2%88%9A5%29*%281%2F2%28-1-%E2%88%9A5%29%29%5En%29*e%5E%28-i*%CF%80*n%29%29%2F%281%2B%E2%88%9A5%29%3B+n%3D7+%E7%B0%A1%E7%B4%84

フィボナッチ数を1回だけ展開してみる

$n≧2$について$F_n=F_{n-2}+F_{n-1}$なので、十分に大きな$n$について、

$len(N(n))=4F_{n-1}+5F_n+4F_{n+1}-6$
　　　　　　$=4(F_{n-3}+F_{n-2})+5(F_{n-2}+F_{n-1})+4(F_{n-1}+F_n)-6$
　　　　　　$=4F_{n-3}+4F_{n-2}+5F_{n-2}+5F_{n-1}+4F_{n-1}+4F_n-6$
　　　　　　$=4F_{n-3}+9F_{n-2}+9F_{n-1}+4F_n-6$

がいえる。

この数式を表にすると、次のような感じになる。

$F_{n-3}$	$F_{n-2}$	$F_{n-1}$	$F_n$	$F_{n+1}$	1
0	0	4	5	4	-6

＝

$F_{n-3}$	$F_{n-2}$	$F_{n-1}$	$F_n$	$F_{n+1}$	1
0	4	5	4	0	-6
4	5	4	0	0	-6

＝

$F_{n-3}$	$F_{n-2}$	$F_{n-1}$	$F_n$	$F_{n+1}$	1
4	9	9	4	0	-6

恐らく同様の表を書けばいくらでも展開できるだろう。展開していくとパスカルの三角形的なものが現れる。


0	0	0	0	0	0	0	4	5	4
0	0	0	0	0	0	4	9	9	4
0	0	0	0	0	4	13	18	13	4
0	0	0	0	4	17	31	31	17	4
0	0	0	4	21	48	62	48	21	4
0	0	4	25	69	110	110	69	25	4
0	4	29	94	179	220	179	94	29	4
4	33	123	273	399	399	273	123	33	4

フィボナッチ数をまとめる

更に、次の式とも等価である。

$len(N(n))=F_n+8F_{n+1}-6$

$F_{n-3}$	$F_{n-2}$	$F_{n-1}$	$F_n$	$F_{n+1}$	1
0	0	0	1	8	-6

https://www.wolframalpha.com/input/?i=x%3DF_%7Bn%7D%2B8*F_%7Bn%2B1%7D-6%3B+n%3D7+%E7%B0%A1%E7%B4%84

NHKから国民を守る党文法

BNFで次のように定義される文法（以下、NHKから国民を守る党文法と省略）を考えてみた。

<expression> ::= 国民
               | NHK
               | <expression> から <expression> を守る党

ここでは必ず動詞「守る」に「～から」節が必須である。この文法は、国民からNHKを守る党や、NHKからNHKからNHKから国民を守る党を守る党を守る党といった、これまでに挙げられていない様々なものから様々なものを防衛する政党を表す文字列を受理する。

なお、NHKからNHKからNHKから国民を守る党を守る党を守る党の意味は、まず国民がNHKからの攻撃を受けていると主張する政党NHKから国民を守る党があり、次にその政党がNHKからの攻撃を受けていると主張する政党NHKからNHKから国民を守る党を守る党があり、そして、その党が同様にNHKから攻撃を受けていると主張する政党を意味する。

表記を簡単にする

NHKから国民を守る党文法のトークンを改変して簡単にすると概ね次のようになる。

<expression> ::= K
               | N
               | <expression> [ <expression> ]

いくつかの例を出そう。

$N(0)$=K=国民
$N(1)$=N=NHK
$N(2)$=N[K]=NHKから国民を守る党
$N(3)$=N[K][N]=NHKから国民を守る党からNHKを守る党
$N(4)$=N[K][N][N[K]]=NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党
$N(5)$=N[K][N][N[K]][N[K][N]]=NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党からNHKから国民を守る党からNHKを守る党を守る党
K[N]=国民からNHKを守る党
N[N[N[K]]]=NHKからNHKからNHKから国民を守る党を守る党を守る党
N[K][K][K][K]=NHKから国民を守る党から国民を守る党から国民を守る党から国民を守る党

NHKから国民を守る党文法の曖昧さ

NHKから国民を守る党文法は、javascript等における第一級関数の呼び出し表記と似ている。いうなれば、NHKから国民を守る党文法を読解することは次のようなjavascriptコードを構文解析することと同等である。

K=function(N){return K};
N=function(K){return N};
N(K)(N)(N(K))(N(K)(N));

この事実は、NHKから国民を守る党文法は非常に難解であるが、読解を行う人間に十分な記憶力があれば確実に読めることを示唆する。

if-if-else問題

確実に読めず曖昧となる例は、C言語における次の構文の例がある（if-if-else問題）。

if(0 <= number)
    if(b < a)
        max = a;
    else
        max = b;

この構文は概ね次のような文法で表される。

<expl> ::= 0 <= number
         | b < a
<line> ::= max = a;
         | max = b;
         | if( <expl> ) <line>
         | if( <expl> ) <line> else <line>

問題の構文を文法に照らし合わせたとき、次のように2通りの構文木が同じ終端記号列を成すことによって、曖昧さが生じてしまう。

if( 0 <= number ) if(b < a) max = a; else max = b;

if( <expl> ) if( <expl> ) <line> else <line>

if( <expl> ) 【 if( <expl> ) <line> else <line> 】
if( <expl> ) 【 if( <expl> ) <line> 】 else <line>

赤い籠の中の鳥

これに近い自然言語の文として、次の物がある。

赤い籠の中の鳥

赤いのは果たして籠か鳥か。

これも同様に文法に照らし合わせると次のようになる。

<名詞> ::= 籠
         | 鳥
         | 赤い <名詞>
         | <名詞> の中の <名詞>

赤い籠の中の鳥

赤い <名詞> の中の <名詞>

赤い 【 <名詞> の中の <名詞> 】
【 赤い <名詞> 】 の中の <名詞>

この文法では籠の中の籠の中の鳥も【籠の中の籠】の中の鳥と籠の中の【籠の中の鳥】という2通りの構文木が生まれる。

似た例（似てないものも含む）
- 【崖の上】のポニョ　上のポニョが崖に張り付いているのではない
- 千葉の【道の駅】　道の駅で一つの名詞
- シャボン玉飛んだ屋根まで飛んだ　飛んだのはシャボン玉だけか？屋根も飛んだのか？
- 〈「お題：飛ぶもの」で〉鳥を落とす勢い
  - 「飛ぶ鳥を落とす勢い」で飛んだのは鳥か？勢いか？
- 【2+3】+4　同じ演算子間での結合優先度よる
- 2^【3^4】　異なる演算子間での結合優先度による

文脈自由文法の曖昧さ

なぜ曖昧になるのかというと同じ終端記号列が複数の構文木に対応してしまうからだが、どういう条件でそうなるのかは筆者はよく知らない。とりあえず手当たり次第取り得る構文木を列挙してみて、終端記号列が1組でも衝突したら曖昧みたいなゴリ押しは考え付くが、どういう条件を満たせば曖昧でないのかは知らない。

ネットで検索したところ、北海道大学のスライドが出てきた。

常に曖昧さを検出できるのか？
もし，曖昧さが検出できた場合，必ずそれを除去できるのか？

任意の文脈自由文法が曖昧か否かを決定できるアルゴリズムは存
在しない．

https://www-alg.ist.hokudai.ac.jp/~thomas/ToC/SLIDES/toc_lec07j.pdf

逆

NHKから国民を守る党文法がjavascriptの関数の呼び出しと似ているということは、逆にMath.sqrt(5)をMath.sqrtから5を守る党のように記述しても曖昧でないということである。

もう少し長い例を挙げる。

Math.sin(Math.sin(Math.sqrt(5)))→Math.sinからMath.sinからMath.sqrtから5を守る党を守る党を守る党

任意の語録の一部分を非終端記号にして文法を作れば、見た目完全に日本語だけどコンピュータに読み込ませるとjavascriptと同等のプログラムが走るみたいなこともできそうである。

関連
- Shakespeare (プログラミング言語) https://ja.wikipedia.org/wiki/Shakespeare_(%E3%83%97%E3%83%AD%E3%82%B0%E3%83%A9%E3%83%9F%E3%83%B3%E3%82%B0%E8%A8%80%E8%AA%9E)

語録置換式大石泉言語

前項のアイデアをもとに一見日本語にしか見えないプログラミング言語を少し考えた。

これはアイドルマスターシンデレラガールズに登場する大石泉のセリフの一部を、名詞句を式として抽出して作ったものである。

凡例：　　　　　非終端記号 ::= 文法 → 意味

<文> ::= <式> は動画を見てれば、覚えられるかな。…いっしょに見る？  → <式>;
       | <式1> は、 <式2> 通りに行動するのに重要な <式3> だよね。 → for (<式1>; <式2>; <式3>) {
       | <式> としてはしゃれっ気なさすぎ？                       → while (<式>) {
       | シンプルが好きだな。                                   → }
       | <式1> が少し短いような…もしかして、これも<式2>…？        → if (<式1>) <式2>;

<式> ::= スカート        → 0
       | ダンス          → 1
       | 世界            → 10
       | 動画            → 100
       | 時間            → null
       | アイドル        → true
       | ストラップ      → false
       | プログラミング   → a
       | 角度            → b
       | ツール          → break
       | 私              → i
       | <式1> の <式2>                         → <式1> + <式2>
       | <式1> として最適化された <式2>           → <式1> = <式2>
       | 私の知らない <式>                       → println(<式>)
       | <式1> をコントロールする <式2>           → <式1> == <式2>

<表現> ::= <文>*

↓プログラム

私として最適化されたスカートは、私をコントロールする動画通りに行動するのに重要な私として最適化された私のダンスだよね。私の知らない私は動画を見てれば、覚えられるかな。…いっしょに見る？私をコントロールする世界が少し短いような…もしかして、これもツール…？シンプルが好きだな。

↓翻訳

for (i = 0; i == 100; i = i + 1) {
  println(i);
  if (i == 10) break;
}

日本語には名詞以外にも動詞やその他の品詞が存在し、さらに入れ子の構造を取らせることも可能である。それらを組み合わせ、言葉選びを十分に吟味すれば読めば何となく何やってるか分かる怪文書も作れるかもしれない。

陣営

NHKから国民を守る党系列$N(n)$では、基本的に陣営はNHK側と国民側に分かれると考えられる。「NHKから国民を守る党」は、国民を守っている一方でNHKと対立しているため、国民側陣営であると考えられる。「NHKから国民を守る党からNHKを守る党」は、NHKを守っているためNHK側陣営とみなせ、かつ国民側陣営と推測される「NHKから国民を守る党」と対立している。

まとめると、次のように偶数番目と奇数番目に分かれて2個の陣営を形成する。

国民側陣営	NHK側陣営
国民	NHK
NHKから国民を守る党	NHKから国民を守る党からNHKを守る党
NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党	NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党からNHKから国民を守る党からNHKを守る党を守る党

これはすべてのNHKから国民を守る党系列の政党に当てはまる。

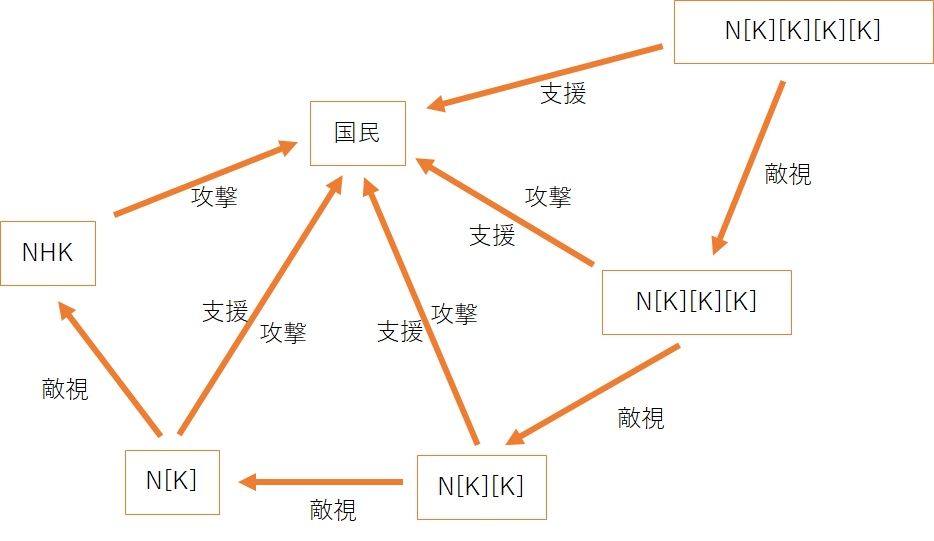
ドロドロの世界

一方、N[K][K][K][K]=「NHKから国民を守る党から国民を守る党から国民を守る党から国民を守る党」ではそう簡単にいかない。

「NHKから国民を守る党」は国民側陣営であると考えられるが、「NHKから国民を守る党から国民を守る党」は、国民を守っているので国民側陣営と思いきや、国民側陣営であるはずの「NHKから国民を守る党」が国民を攻撃しているとみなして応戦している。この世界では、「NHKから国民を守る党から国民を守る党」にとって、「NHKから国民を守る党」は国民側陣営ではないのだ。それでいながら、「NHKから国民を守る党」は国民を守っていると主張している。ドロドロな世界である。そしてその状況がもう2回続くのである。

NHKと各政党が国民に対して様々な影響を及ぼしあい、ほとんどの組織は自分は国民を守っていると主張しているが、他の集団の目には攻撃を加えているように映っている。怖い世界である。

矛盾した政党名

同一の言葉で表される集団は同一の集団であるとみなすと、単体で矛盾を生んだ政党名を作り出すことができる。

最も簡単なものはN[N]=「NHKからNHKを守る党」である。これではNHKが自殺行為をしているようである。N[N][N[N]]=「NHKからNHKを守る党からNHKからNHKを守る党を守る党」も見た目は整っているが、何がやりたいのかさっぱり分からない。

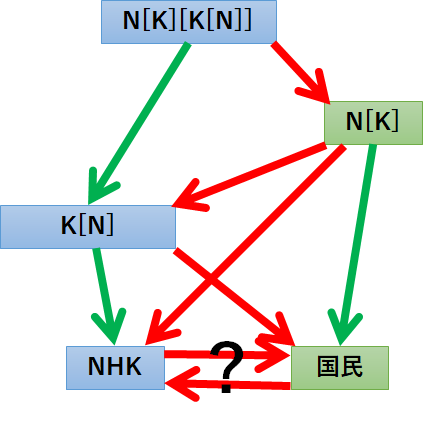
矛盾した世界

なぜ矛盾が生じるのだろうか。とりあえず、政党名は飽くまでその政党自身の主張であり、事実を正確に表してはいないという可能性を認めたら、世界観的には面白いが、数学的には何でもアリになってつまらないので、ここでは政党名は必ず事実を正確に表していると仮定する。また、同じ文字列で表される組織は同一の組織であると仮定する。

最もわかりやすいケースは、ある組織Aが別の組織Bに対して防衛支援を行っているときに、別の組織によってAがBに攻撃を加えていることにされてしまった場合である。政党名の構文木のノードとして「AからBを守る党=C」というものが現れた際には、「CがBに防衛支援をしている」「AがBに攻撃を加えている」「CがAを敵視している」という三つの事実が生じる。これによって、最終的にすべての組織の間で友好的か敵対的かどちらの情報もないかが決定されるわけだが、友好的と敵対的という情報が衝突してしまった場合に矛盾は発生する。

また、次のような場合も陣営分けが不可能となる。

N[K][K[N]][N]=「NHKから国民を守る党から国民からNHKを守る党を守る党からNHKを守る党」。この世界にはK[N]=「国民からNHKを守る党」が存在し、それは「NHK」と友好的なはずである。また、N[K][K[N]]=「NHKから国民を守る党から国民からNHKを守る党を守る党」も存在し、K[N]=「国民からNHKを守る党」と友好的なはずである。すると、N[K][K[N]]=「NHKから国民を守る党から国民からNHKを守る党を守る党」はNHKとも友好的と考えてもよさそうなものである（味方の味方は味方と仮定する）。しかしながら、この世界にはN[K][K[N]][N]=「NHKから国民を守る党から国民からNHKを守る党を守る党からNHKを守る党」という政党が存在し、この政党はN[K][K[N]]=「NHKから国民を守る党から国民からNHKを守る党を守る党」がNHKを攻撃していると主張している。これは主張が矛盾していることになる。

このような、互いの主張をまとめると何処かで陣営分けが破綻する世界を矛盾した世界と呼ぶこととする。

ランク

政党名の入れ子の回数について考えてみる。国民やNHKは何も守っていないので入れ子の回数は0。「NHKから国民を守る党」は、入れ子の回数が0の対象から、入れ子の回数が0の対象を守っているので、入れ子の回数は1。ここでは入れ子の回数をランクと呼ぶこととする。また、ランクが0の組織を終端組織と呼ぶこととする。

関連
- https://qiita.com/POPOPON/items/bf94453cba0e384b269d#%E8%A3%9C%E9%81%BAa%E7%9F%9B%E7%9B%BE%E3%81%97%E3%81%AA%E3%81%84%E6%94%BF%E5%85%9A%E3%81%AF%E3%81%A9%E3%82%8C%E3%81%8F%E3%82%89%E3%81%84%E5%AD%98%E5%9C%A8%E3%81%99%E3%82%8B%E3%81%8B

政党名のランクは、政党名が直接含んでいる2個の組織のランクの大きい方に1を加えた値だ。

組織名	ランク
NHK	0
国民	0
NHKから国民を守る党	1
国民からNHKを守る党	1
NHKから国民を守る党から国民からNHKを守る党を守る党	2

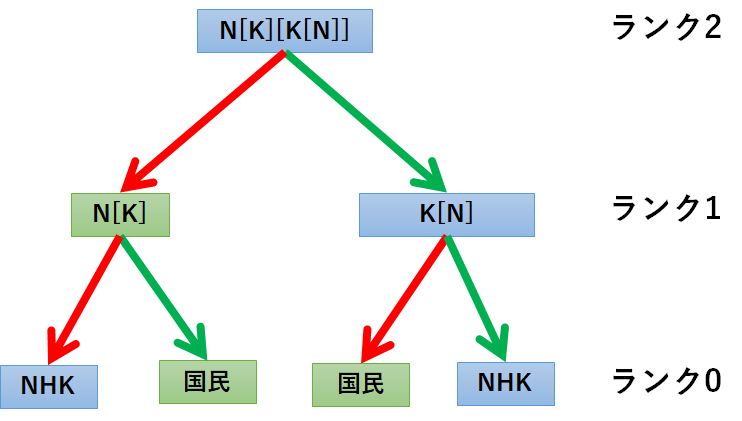
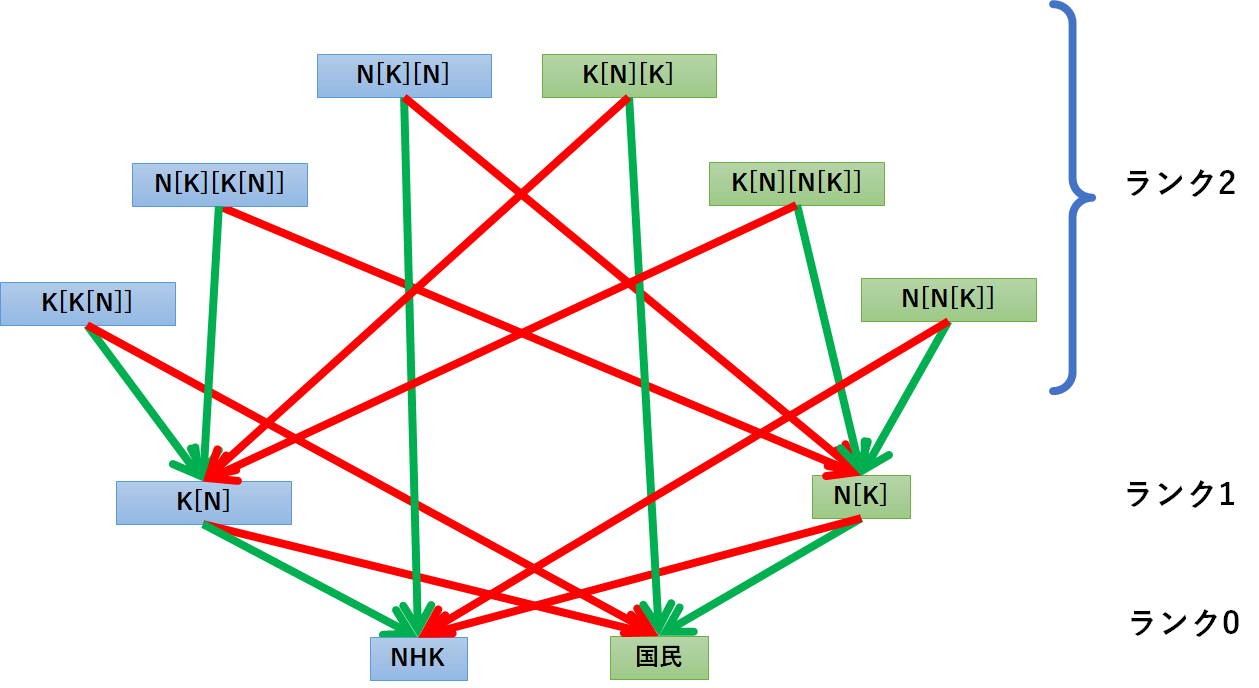
以下のように同じランクを横に並べて樹形図を描くと、もっと直感的に分かりやすくなる。

根源組織

政党のランクは、必ず政党名に直接含む2個の組織のランクよりも1以上大きい。したがって、政党名に含まれる組織を順に辿っていくと、いつかは必ず終端組織に辿り着くということがいえる。

政党とその政党が守る対象は同じ陣営であるため、すべての政党はNHKか国民のどちらかの陣営に所属することとなる。ある組織Aについて、守る対象をひたすら辿って辿り着いた終端組織を、Aの根源組織と呼ぶこととする。

政党名から根源組織を素早く判断するには、その政党名の最も右側に出てくる終端組織がどちらかを考えればよい。文法上、政党名を、その政党が守る対象に置換する操作を繰り返すと、右側が残り続けるからだ。

組織名
NHKから国民を守る党から国民からNHKを守る党を守る党
国民からNHKを守る党
NHK

また、このような世界にはどちらの陣営にも所属しない第三勢力が生まれることがないということが、ここからいえる。

ヒエラルキー

ところで、N[N[K]]=「NHKからNHKから国民を守る党を守る党」は、「NHK」に対抗するはずの「NHKから国民を守る党」を、さらに「NHK」の手から守っている。これでは「NHKから国民を守る党」の立場がないのではないだろうか。そこで、「AからBを守る党=C」という政党名があった時に、「CはAより強い」という序列が発生すると考えてみる。

また、NHKと国民の戦闘力が均衡している場合にも、「NHKから国民を『守る』党」という表現には少し違和感がある。「守る」というからには国民はNHKに対して弱者であるはずである。なので、ここでは「AからBを守る党」という政党名に対して、「AはBより強い」という事実を主張していることを想定する。

まとめると、「AからBを守る党=C」に対して、「C＞A＞B」となる。

互いの主張をまとめると何処かで序列に反する世界を、ヒエラルキーに反した世界と呼ぶこととする。

矛盾した世界のように、ヒエラルキーに反した世界にも少し複雑な例を考えてみる。

N[K][K[N]]=「NHKから国民を守る党から国民からNHKを守る党を守る党」。

N[K]=「NHKから国民を守る党」は、単体で見れば、「NHK＞国民」である。また、K[N]=「国民からNHKを守る党」も、単体で見れば「国民＞NHK」となっている。しかし、この二つの政党を同じ世界に共存させると、上記のヒエラルキーの原理に反してしまう。

TODO

解決問題

政党名を与えたとき、世界が矛盾しているか否かを判定するアルゴリズムは存在するか？
- https://qiita.com/kb10uy/items/5b146c4494fdd8f8758c#4-%E7%9F%9B%E7%9B%BE%E3%81%97%E3%81%9F%E4%B8%96%E7%95%8C%E3%81%8B%E3%81%A9%E3%81%86%E3%81%8B%E3%82%92%E5%88%A4%E5%AE%9A%E3%81%99%E3%82%8B
矛盾のある世界において、NHKと国民を友好の線で結ぶことはできるか？
- できない。矛盾のありなりに関わらず、組織はただ一つの終端組織を持つ。

未解決問題

陣営の構成組織数を簡単に求めるアルゴリズムは存在するか？
NHKと国民以外の初期勢力が与えられた場合、どのように変化するか？
「～から」「～を」節を省略可能とするとどのような変化があるか？
「国民がNHKと仲良くしているのが気に食わない党」のような主張に変化のある党の場合はどうなるか？
ある政党名がヒエラルキーに反しない矛盾のない政党名かを判断するアルゴリズムは存在するか？
国民およびNHKからなる任意個の組織列を与えたとき、その順番に登場するヒエラルキーに反しない矛盾のない政党名を考えることはできるか？
- 例えばNHK　国民　国民　国民　NHK　国民　NHK　国民　NHK　NHK　NHK　国民の順番で現れるヒエラルキーに反しない矛盾のない政党名を挙げられるか？

大石泉すき兄貴すき兄貴すき大石泉すき兄貴

「大石泉すき兄貴すき兄貴すき大石泉すき大石泉すき兄貴」には、何通りの解釈が存在するか？
- 「大石泉すき（大石泉すき兄貴）」は、大石泉がすきであることが既に分かっている「大石泉すき兄貴」に対して、さらに「大石泉すき」と付け加えているため、不自然である。
  - 関連
    - グライスの協調の原理 https://ja.wikipedia.org/wiki/%E8%AA%9E%E7%94%A8%E8%AB%96#%E3%82%B0%E3%83%A9%E3%82%A4%E3%82%B9%E3%81%AE%E5%8D%94%E8%AA%BF%E3%81%AE%E5%8E%9F%E7%90%86
    - 話題化 https://ja.wikipedia.org/wiki/%E8%A9%B1%E9%A1%8C%E5%8C%96
    - 焦点 (言語学) https://ja.wikipedia.org/wiki/%E7%84%A6%E7%82%B9_(%E8%A8%80%E8%AA%9E%E5%AD%A6)
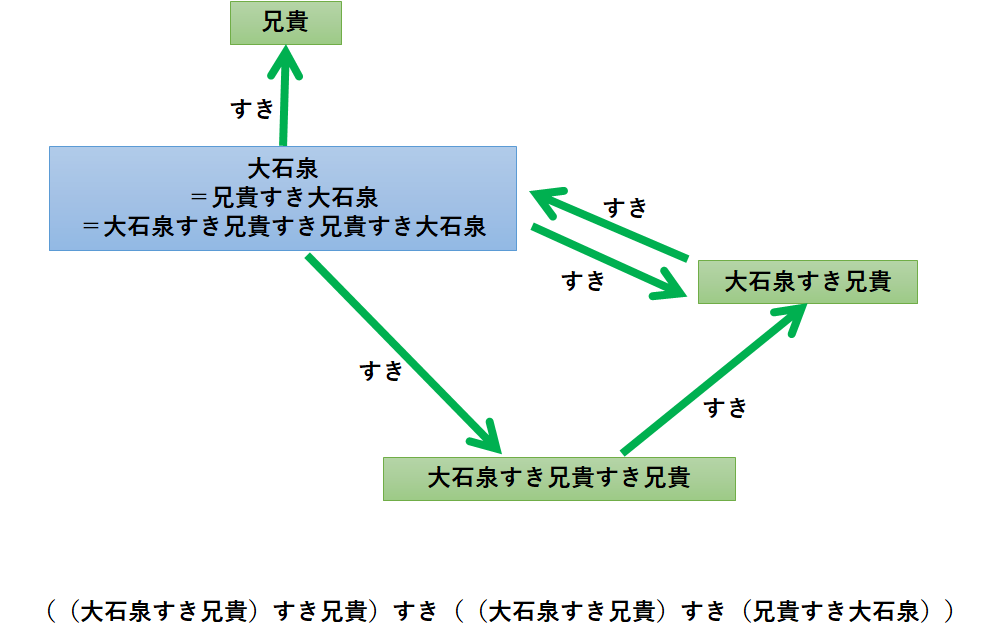
- 「すべての修飾句は新情報を与えなければならない」（ここでは無駄のないと呼ぶ）とすると、「大石泉すき（大石泉すき兄貴）」は、左側の「大石泉すき」が余計であるため非文である。そのため、「大石泉すき大石泉すき兄貴」の構造は、「（大石泉すき大石泉）すき兄貴」＝「自分自身のことが大好きな大石泉と、そんな大石泉のことが大好きな兄貴」の1択に絞られる。
- 1通りの「無駄のない解釈」しか生み出さない大石泉すき兄貴構文はいくつあるか？
- さらに、「大石泉すき大石泉」も特徴的な構造をしている。すきの動作主と対象を線で結ぶと、自分自身に対して帰ってきてしまう。自分のことが大好きな大石泉は文学的には面白いが、考え出すと図がえらいことになるので、自分自身に対してすきと公言することをナルシストと呼んで特別扱いをすることとする。
- まとめると、「大石泉すき大石泉すき兄貴」にはナルシストのない無駄のない解釈が存在しない。
- また、大石泉は一人しかいないが、兄貴は沢山居得る。「大石泉すき兄貴すき兄貴」には、「（大石泉すき兄貴）すき兄貴」＝「大石泉のことが好きな兄貴、そんな大石泉すき兄貴のことが好きな兄貴（大石泉がすきとは言っていない）」と、「大石泉すき（兄貴すき兄貴）」＝「大石泉およびとある兄貴のことがすきな兄貴」という2通りの解釈が存在するが、どちらも2回出てくる兄貴が同じ存在であるとは限らない。
- 最初の例題にはナルシストのない無駄のない解釈が何通り存在するか？
- その他のナルシストのない無駄のない解釈の例
  - 例：「大石泉すき兄貴すき大石泉すき兄貴」
    - 「（大石泉すき兄貴）すき（大石泉すき兄貴）」：ナルシストも無駄もない
    - 「（（大石泉すき兄貴）すき大石泉）すき兄貴」：ナルシストも無駄もない
    - 「（大石泉すき（兄貴すき大石泉））すき兄貴」：大石泉がナルシスト
    - 「大石泉すき（（兄貴すき大石泉）すき兄貴）」：右端の兄貴が2回大石泉がすきなので無駄
    - 「大石泉すき（兄貴すき（大石泉すき兄貴））」：右端の兄貴が2回大石泉がすきなので無駄
  - 例：「兄貴すき大石泉すき大石泉」
    - 右端の大石泉は左側に出てくる1個以上の対象がすきでなければならないが、その中には必ず大石泉を含むので必ずナルシストになる
  - 例：「大石泉すき大石泉すき兄貴すき大石泉すき兄貴」
    - 左端の大石泉は必ず誰かにすかれなければならないが、大石泉にすかれるとナルシストになるのでできない。同一の実体を持つ兄貴に対して大石泉すきと言えるのは最大1回なので、大石泉のほうが多いと大石泉が余って無駄にならざるを得ない。
  - 例：「兄貴すき大石泉すき大石泉すき兄貴すき兄貴すき大石泉すき大石泉すき兄貴」
    - 右端の大石泉は右から2番目の大石泉をすきと言えないので、右から2番目の大石泉は右端の兄貴にすかれなければならない。しかしそれは無駄になるのでできない。
    - 大石泉を消費する兄貴が大石泉よりも右に居なければ必ず無駄になる。
      - 「右からn個取ってきたときに、そこに大石泉の方が多い」ようなnがあると無駄が生まれざるを得ない。
  - 例：「大石泉すき兄貴すき大石泉すき大石泉すき大石泉すき兄貴すき兄貴すき兄貴」
    - 「（大石泉すき兄貴）すき（大石泉すき（（大石泉すき（（大石泉すき兄貴）すき兄貴））すき兄貴））」
- 冒頭のあれには右側3個の中に大石泉が多く存在するので、ナルシストのない無駄のない解釈は存在しない。

兄貴集合仮説

しかし、「大石泉すき兄貴すき兄貴」は、「大石泉すき兄貴のことがすきな兄貴」で違和感はないけど、「大石泉すき兄貴すき大石泉すき兄貴」というと、「自分たちのことが好きな大石泉すき兄貴」に見えてしまう。
- そもそもここでいう兄貴は「～な人」程度のことを意味する形式的な言葉であり、特定の個人を指す言葉ではない。
- 「大石泉すき兄貴すき兄貴」は「大石泉が好きな人が好きな人」を意味する。
- そして、「～な人」という表現は性質を表す表現で、一人の人間が複数の「～な人」に該当することも考えられる。
- ⇒「大石泉すき兄貴すき兄貴」は、全兄貴の中で、「大石泉すき兄貴」が好きな兄貴の集合である。
  - 「大石泉すき兄貴」は「兄貴」の部分集合。
  - 「大石泉すき兄貴すき兄貴」は「兄貴」の部分集合。
  - 「大石泉すき兄貴すき大石泉すき兄貴」は「大石泉すき兄貴」の部分集合。
  - 「大石泉すき兄貴」の中には、自分たちのことがすきな兄貴とそうでない兄貴がいる。前者は「大石泉すき兄貴すき大石泉すき兄貴」と呼ばれる。
  - ナルシスト判定を「AすきB」において、BがAの部分集合であってはならないという規則にするべき？
    - 例：「大石泉すき兄貴（=A）すき兄貴（=B）」は、「兄貴（=B）」は「大石泉すき兄貴（=A）」の部分集合ではないのでセーフ。
    - 例：「兄貴（=A）すき大石泉すき兄貴（=B）」は、「大石泉すき兄貴（=B）」は「兄貴（=A）」の部分集合なのでNG。
      - 以前は同じ兄貴でも別の兄貴を指すと解釈していたのでセーフだったが、部分集合であってはならない規則によってNGになった。


0	0	0	0	0	0	0	4	5	4
0	0	0	0	0	0	4	9	9	4
0	0	0	0	0	4	13	18	13	4
0	0	0	0	4	17	31	31	17	4
0	0	0	4	21	48	62	48	21	4
0	0	4	25	69	110	110	69	25	4
0	4	29	94	179	220	179	94	29	4
4	33	123	273	399	399	273	123	33	4


0	0	0	0	0	0	0	4	5	4
0	0	0	0	0	0	4	9	9	4
0	0	0	0	0	4	13	18	13	4
0	0	0	0	4	17	31	31	17	4
0	0	0	4	21	48	62	48	21	4
0	0	4	25	69	110	110	69	25	4
0	4	29	94	179	220	179	94	29	4
4	33	123	273	399	399	273	123	33	4

【数学】NHKから国民を守る党からNHKを守る党からNHKから国民を守る党を守る党

背景