はじめに
OpenFOAMの境界条件のexprFixedValueを使用すれば、controlDictに設定したprobesのfunction objectで取得した指定位置での温度に応じて、流入温度をPID制御をすることができます。
この方法では、OpenFOAMのexpressions syntaxの機能とFunction1のfunctionObjectValueの機能を使用しています。
Function1については、こちらの記事で説明をしています。
サンプルモデル
赤点がセンサー点です。ここの温度が20℃になるように、流入温度を制御しています。
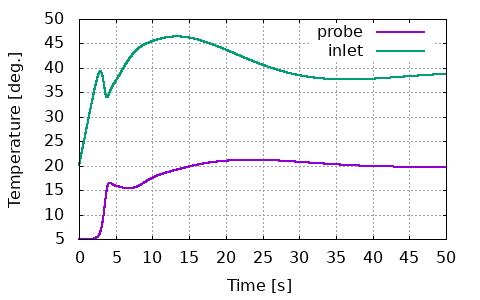
センサー点での温度(probe)と流入温度(inlet)の履歴のグラフです。センサー点の温度が徐々に20℃に近づいていることが確認できます。
こちらのサンプル2:sample_probe_PIDにOpenFOAM v2212で動作確認をしたサンプルモデルが置いてあります。
説明
このサンプルで設定されている制御の仕組みについて説明します。
probes
解析結果からのセンサー点の温度の取得は、system/controlDictに設定しているprobesのfunction objectを使っています。ここでは、probeLocationsにセンサー点の座標値を指定しています。
probeTemperature
{
type probes;
libs (sampling);
name probes;
writeControl timeStep;
timeInterval 1;
fields (T);
probeLocations
(
(0.025 0.025 0.005)
);
}
ここで取得した温度は、postProcessing/probeTemperature/0/Tファイルに時系列データとして保存されます。
inletパッチの温度の境界条件
流入境界であるinletパッチでの温度の境界条件は、以下のように、exprFixedValue 1 を使用しています。
exprFixedValueの境界条件はここで説明しているPatchFunction1のexpressionのタイプが設定できる境界条件です。
inlet
{
type exprFixedValue;
functions<scalar>
{
probeTemperature
{
type functionObjectValue;
functionObject probeTemperature;
functionObjectResult average(T);
defaultValue 278.15;
}
}
storedVariables
(
{
name I;
initialValue "0.0";
value
{
resultType scalar;
valueType scalar;
isSingleValue true;
value 0.0;
}
}
{
name dTOld;
initialValue "15.0";
value
{
resultType scalar;
valueType scalar;
isSingleValue true;
value 15.0;
}
}
);
variables
(
"KP = 1.0"
"KI = 0.5"
"KD = 0.2"
"dT = 293.15 - fn:probeTemperature()"
"I = I + dT*deltaT()"
"D = (dT - dTOld)/deltaT()"
"dTOld = dT"
);
valueExpr "KP*dT + KI*I + KD*D + 278.15";
value uniform 278.15;
}
これ以降では、このexprFixedValueの各設定項目について説明します。
probesで取得したセンサー点の温度の参照
以下の部分で、probesのfunction objectで指定したセンサー点での温度の値を、境界条件の中で参照するためのFunction1で記述された関数を定義しています。
functions<scalar>
{
probeTemperature
{
type functionObjectValue;
functionObject probeTemperature;
functionObjectResult average(T);
defaultValue 278.15;
}
}
このようにfunctions<scalar>の部分で、Function1の関数を定義すると、「fn:{Function1の関数の名前}()」(この例の場合はfn:probeTemperature())と記述することで、この関数から返される値を参照することができます。
Function1のタイプはfunctionObjectValueを指定しています。このfunctionObjectValueでは、以下の値を設定します。
functionObject
値を参照するfunction objectの名前を設定します。
functionObjectResult
参照する値の種類を設定します。
ここに設定することができる名前は、各function objectのソースコードで定義されていますが、結果の時刻ディレクトリ以下にあるuniform/functionObjects/functionObjectPropertiesファイルでも調べることができます。一度、function objectを設定して計算を実行して、このファイルの出力を確認してみるとよいと思います。
このサンプルの場合には、以下のように出力されています。これから、目的の設定値がaverage(T) 2 だということが分かります。
cdf7e925f5746741c316f5fbcf39ad0dfca90775
{
probeTemperature
{
scalar
{
average(T) 278.1500756750618;
min(T) 278.1500756750618;
max(T) 278.1500756750618;
}
label
{
size(T) 1;
}
}
defaultValue
最初の時刻など、まだfunction objectが実行されずに、値を参照できない場合に返される値を設定します。これは、オプションです。
別の方法
probeTemperatureの設定を次のようにすると、function objectで取得した値を参照するのではなく、この境界条件内でセンサー点での温度を取得することもできます。
functions<scalar>
{
probeTemperature
{
type sample;
field T;
position (0.025 0.025 0.005);
}
}
保存される値(storedVariables)
PID制御では、目標値$r(t)$と制御量(この場合はセンサー点での温度)$y(T)$との差である偏差を$e(t)=r(t)-y(t)$としたとき、制御入力(この場合は流入境界での温度)$u(T)$は、以下のように表すことができます。
u(t)=K_p e(t)+K_i \int_0^t e(\tau) d\tau + K_d \frac{d e(t)}{dt}
ここで、$K_p$、$K_i$、$K_p$は、それぞれ比例ゲイン、積分ゲイン、微分ゲインです。
この式を離散化をして考えると、積分項は
\int_0^t e(\tau) \tau \simeq \sum_{\tau=0}^{t-\Delta t} e(\tau) d\tau + e(t) \Delta t
と書くことができ、微分値は
\frac{d e(t)}{dt} \simeq \frac{1}{\Delta t} \bigl(e(t) -e(t-\Delta t) \bigr)
と書くことができます。つまり、これらの値を計算するためには、前のイタレーションまでの偏差の積分値と、前のイタレーションでの偏差の値が必要になります。
このような前のイタレーションでの値を保存できる変数をstoredVariablesを使って定義をすることができます。
storedVariables
(
{
name I;
initialValue "0.0";
value
{
resultType scalar;
valueType scalar;
isSingleValue true;
value 0.0;
}
}
{
name dTOld;
initialValue "15.0";
value
{
resultType scalar;
valueType scalar;
isSingleValue true;
value 15.0;
}
}
);
ここでは、前のイタレーションまでの偏差の積分値を保存する変数Iと前のイタレーションでの偏差の値を保存する変数dTOldが定義されています3。
各変数の定義と計算(variables)
variablesの部分で各変数(パラメータ)の定義と計算を行っています。
variables
(
"KP = 1.0" // 比例ゲイン
"KI = 0.5" // 積分ゲイン
"KD = 0.2" // 微分ゲイン
"dT = 293.15 - fn:probeTemperature()" // 偏差
"I = I + dT*deltaT()" // 偏差の積分値の計算
"D = (dT - dTOld)/deltaT()" // 偏差の微分値の計算
"dTOld = dT" // 現在の偏差の値をdTOldに保存
);
ここで、deltaT()は解析での時間刻みです。
境界条件値の設定(valueExpr)
valueExprで境界条件値を設定します。ここでは、制御入力$u(T)$の値を計算して設定しています。
valueExpr "KP*dT + KI*I + KD*D + 278.15";
おわりに
このようにOpenFOAMでもexpressions syntaxやPatchFunction1の機能を使用すれば、C++のソースコードを書かなくても、境界条件の設定などだけで、かなり複雑なことができるようになります。
(新しく境界条件を作ってしまったほうが早いという話もありますが…)
expressions syntaxについは、公式にもここで説明されていますが、ここに書かれている以外にも説明されていない機能が実装されています。ただし、まだバグや思いもよらない制限などがありそうなので、使う場合にはよく検証を行ってから使ったほうがよいです。
-
uniformFixedValueの境界条件を使って、expressionのタイプを指定しても同様の設定をすることができますが、この場合は、リスタート計算に必要な情報のうち結果ファイルに保存されないものがありますので(バグ?)、exprFixedValueで設定することをお勧めします。 ↩ -
もちろんこの場合は、
min(T)やmax(T)を使っても同じ結果が得られます。 ↩ -
このexpressionの表現は、パッチ上での値(patchExpr)として使用されています。patchExprでは定義された変数はそのパッチの各要素に値を持ちますが、
IとdTOldの値は1つのスカラーの値です。このような場合は、初期化に問題が生じるようなので、設定にisSingleValue true;などを記述することが必要です。 ↩
