はじめに
物質に刺激(例えば電場)を与え応答(例えば電流)を見ることで物質の性質を調べることは物性物理の基礎ですが、実際にシミュレーションや数値計算をするのは結構大変です。
そこで量子輸送現象を簡単に解析できるオープンソースのpython用モジュール"Kwant"を紹介します。
Kwantとは
Kwantはグルノーブル原子力研究センターとデルフト工科大学の研究者たちによって現在も精力的に開発されている強束縛模型ソルバです。論文にもなっています。本家HPのドキュメントが非常に充実しており、それにしたがってポチポチしていくだけで物理的に面白い計算例を手元で簡単に再現・拡張することができます。強束縛模型で書ける系であれば、電極端子まで含めて非常に簡単に定義でき、波動関数や状態密度、Landauer-Buttiker公式や久保公式を用いた輸送計算などを総合的にカバーしています。
自分も以前研究の一環でKwantを使ってみようと思っていたのですが、日本語の記事やコミュニティがほぼ存在せず、また当時はpythonなんて何も知らなかったため導入を後回しにしてしまっていました。なんと発音するのかすらわかりません。今回暇ができた&pythonに慣れてきたこともあり、ついに使ってみたのでその様子を紹介したいと思います。
※物理の理解・モジュールの理解の両面で誤りを含む可能性が大いにあります。自己責任でご覧ください。英語が読める方は本家を参考にした方がいいかもしれません。
メソスコピック系
Kwantでは主にメソスコピック系と呼ばれる物理系を解析の対象にします。メソスコピックというのは要は原子レベルに小さいデバイスだと閉じ込めとか干渉とかの量子効果が輸送を支配するよ~って話です。特に端子が量子状態や輸送に影響を与えてくるあたりが面白いところです。
物理のおさらいは本家でもお勧めされてるSupriyo Dattaの “Electronic transport in mesoscopic systems”か"量子輸送 基礎編 ナノスケール物性の基礎"のシリーズを読んでもらうとして、ここでは踏み込みまず、実装に重きを置きます。
まず、やってみる。それから考える。
インストール
pythonの環境構築はできているものとします。Anacondaを用いてpython環境を作った場合は
conda install -c conda-forge kwant
で一発インストールできます。現在の最新版はv1.4です。pipだと苦労するらしいので本家の手順を参考にしてください。
例1:コンダクタンスの量子化
まず、もっとも単純な例として二次元の長方形型デバイスの両端に端子を付け、その間の伝導度を計算してみます。ここと本家ドキュメントの2.2.2章と2.2.3章を参考にしています。
Kwantではまず格子形状と系を定義(Build)します。
# 基本モジュールのインポート
import kwant
import numpy as np
import scipy as sp
import math
import matplotlib.pyplot as plt
%matplotlib inline
# パラメータ
W=10 #デバイス幅
L=30 #デバイス長さ
t=1 #最近接ホッピング
a=1 #格子定数
# 格子形状と系の定義
lat = kwant.lattice.square(a)
syst = kwant.Builder()
これで格子形状latと系systが定義されます。このままではsystはガワだけ定義された空っぽの状態なので中身を埋めていきます。ここでいう中身は、系のタイトバインディング(強束縛)ハミルトニアンです。
# オンサイトポテンシャル
syst[(lat(x, y) for x in range(L) for y in range(W))] = 0
# 最近接ホッピング(y方向)
syst[((lat(x, y),lat(x,y-1)) for x in range(L) for y in range(1,W))] = -t
# (x方向)
syst[((lat(x, y),lat(x-1,y)) for x in range(1,L) for y in range(W))] = -t
これで幅W長さLのタイトバインディングハミルトニアンがsystに格納されます。ホッピングは片方向のみを定義すれば、ハミルトニアンがエルミートになるよう逆方向のホッピングも良いかんじに定義してくれます。for x in range(L)とかはpythonの内包表記です。
次にリード(電極端子)を定義します。リードは半無限に一方向に伸びているものとして、その方向を指定します。ここではまず系の左側に付ける端子を定義するので、(-1,0)方向を指定します。リードのオンサイトポテンシャルやホッピングもsystと同様に定義できますが、x座標が0と1の点たちだけを定義すればTranslationalSymmetry((-a, 0))によって周期的に左方向に繰り返してくれます。
# リード定義
lead = kwant.Builder(kwant.TranslationalSymmetry((-a, 0)))
# オンサイトポテンシャル
lead[(lat(0, j) for j in range(W))] = 0
# 最近接ホッピング
lead[((lat(0, j), lat(0, j - 1) ) for j in range(1,W))] = -t
lead[((lat(1, j), lat(0, j ) ) for j in range(0,W))] = -t
これで左側に無限に伸びるリードが定義できましたが、systとはまだ独立していますので、くっつけます。
syst.attach_lead(lead)
これだけです。
次に反対の右側にもリードをくっつけます。いったん定義したリードをひっくり返して逆側に付けるには
syst.attach_lead(lead.reversed())
これだけです。簡単です。
さてここまでで長方形の試料と二つのリードleadがくっつけられた状態がsystに格納されているはずです。Kwantは系の可視化にも優れており、どういう系が設計されているかを一目で確認することができます。
kwant.plot(syst)
青い点が試料の格子点、赤い点がリードの格子点、線があるところにはホッピングが定義されています。試料の両端にきれいにリードが端子付けされているのがわかります。満足したら設計を完了します。
syst = syst.finalized()
これで端子を含めた系の設計が完了しました。
次に、できた系の端子間の伝導度を計算してみます。Landauer公式によれば、端子間伝導度は端子間の量子力学的な透過確率(平面波を入射して真ん中で波動関数を接続して色々して求めたアレです。)に$e^2/h$を掛けたものに等しいですので、透過率を計算します。透過率はkwant.smatrix()クラスにfinalizeされたsystと入射波のエネルギーを与えることで計算できます。
conductance = []
energies = np.linspace(-4,-3,50)
for energy in energies:
#散乱行列(S行列)の定義
smatrix = kwant.smatrix(syst, energy)
#リード0から1への透過確率を計算、格納。
conductance.append(smatrix.transmission(1, 0))
# プロット
plt.plot(energies, conductance)
plt.grid()
plt.xlabel("energy/t")
plt.ylabel("conductance($e^2/h$)")
plt.show()
簡単です。リードにはattach_leadした順に0,1,2...と番号が振られていくので今回は1と0を指定しています。得られた結果を見ると、入射波のエネルギーを上げていくと階段状に伝導度が増えていくことがわかります。これはコンダクタンスの量子化というメソスコピック系に特有な効果で、y方向への量子力学的な閉じ込め効果がその起源です。
振り返ってみると、試料のハミルトニアンの定義、リードのハミルトニアンの定義、リードの接着、伝導度の計算を20行程度のコードで実行することができました。同様の計算を1からやろうとすると、リードの表面グリーン関数の計算やリード-試料間のホッピングの定義など、物理的にもコーディング的にもかなりの労力がかかることを思うと、素晴らしく簡便です。
おまけ(スピン自由度)
スピン空間の単位行列をs0=np.array([[1,0],[0,1]])と定義してこの例でtと書いたところをt*s0に置き換えることでスピン縮退を表現でき、コンダクタンスが2倍になります。同様にPauli行列を定義すればスピン軌道相互作用やZeeman磁場を与えることもできます。
例2:量子ホール効果
例1に加えて非一様なオンサイトポテンシャルやホッピングを扱う例として、乱れた系の量子ホール効果を考えてみます。ついでに端子が多数になった場合の扱いに注意が必要になります。本家のドキュメントのあちこちを参考にしています(以下同様)
デバイスが存在する2次元面内に垂直に磁場が印加された状況を仮定し、実験でよく見るホールバーの配置に合わせて、端子を6個くっつけていきます。kwantやnumpyのimportは上の例と共通なので省略します。まずはデバイスの形などの定義です。追加のパラメータにのみコメントを付けています。
W=15
L_lead=6 #ホールリードの幅
M_lead=6 #ホールリードの端からの距離
L=30
t=1
a=1
V=0.05 #ランダムポテンシャルの強さ
lat = kwant.lattice.square(a)
syst = kwant.Builder()
次に試料部分のハミルトニアンを定義します。オンサイトポテンシャルは正規乱数を用いて適当に与えます。ここでも最近接のみのホッピングを考えることとし、垂直磁場によるパイエルス位相を考慮に入れます。
# オンサイトのランダムポテンシャル
for x in range(L):
for y in range(W):
syst[lat(x, y)] = np.random.randn()*V
# (xi, yi)から(xj, yj)へのホッピングを与える関数
def hopping(site_i, site_j, phi):
xi, yi = site_i.pos
xj, yj = site_j.pos
return -t*np.exp(-0.5j * phi * (xi - xj) * (yi + yj))
# 最近接ホッピング
syst[lat.neighbors()] = hopping
リードのハミルトニアンの指定方法として、例1と異なり、lat.neighbors()を使ってみました。これはすでに定義されたサイト点の最近接のホッピングを定義する際に使え、わざわざ座標を指定しなくてよいので便利です。ちなみにn=2をパラメータとして与えると次近接のホッピングも同様に定義できます。
ホッピングを定義する関数hoppingは1つ目と2つ目の引数に移動元、移動先のサイト情報が入り、それ以降の引数は外から与えるパラメータとして解釈されます。ここで磁場の大きさを表すパラメータphiはこの時点では値を持たず、systをfinalizeしたのちに外から値を与えることができます。たとえば伝導度などの何らかの応答のパラメータ依存性を見たいとき、わざわざパラメータの値ごとにsystを定義しなおし、finalizeする必要がなくなります(後述)。
次に6個のリードを順番に定義します。両端に付けた2つの端子以外の4つの端子はy方向に延びる端子なのでkwant.TranslationalSymmetry((0, a))となっていることに注意してください。各lat.neighbors()を愚直に書いた場合のコードもコメントアウトして載せてあります。
lead = kwant.Builder(kwant.TranslationalSymmetry((-a, 0)))
lead[(lat(0, j) for j in range(W))] = 0
# lead[((lat(0, j), lat(0, j - 1) ) for j in range(1,W))] = hopping
# lead[((lat(1, j), lat(0, j ) ) for j in range(0,W))] = hopping
lead[lat.neighbors()] = hopping
lead_hall24 = kwant.Builder(kwant.TranslationalSymmetry((0, a)))
lead_hall24[(lat(j, 0) for j in range(M_lead,M_lead+L_lead))] = 0
# lead_hall24[((lat(j,0), lat(j-1,0) ) for j in range(M_lead+1,M_lead+L_lead))] = hopping
# lead_hall24[((lat(j,1), lat(j ,0) ) for j in range(M_lead,M_lead+L_lead))] = hopping
lead_hall24[lat.neighbors()] = hopping
lead_hall35 = kwant.Builder(kwant.TranslationalSymmetry((0, a)))
lead_hall35[(lat(j, 0) for j in range(L-M_lead-L_lead,L-M_lead))] = 0
# lead_hall35[((lat(j,0), lat(j-1,0) ) for j in range(L-M_lead-L_lead+1,L-M_lead))] = hopping
# lead_hall35[((lat(j,1), lat(j ,0) ) for j in range(L-M_lead-L_lead,L-M_lead))] = hopping
lead_hall35[lat.neighbors()] = hopping
# 全6本のリードの取り付け。順番に注意。
syst.attach_lead(lead)
syst.attach_lead(lead.reversed())
syst.attach_lead(lead_hall24)
syst.attach_lead(lead_hall35)
syst.attach_lead(lead_hall24.reversed())
syst.attach_lead(lead_hall35.reversed())
ここまででデバイスの全様が定義されました。可視化してfinalizeしておきます
kwant.plot(syst)
syst = syst.finalized()
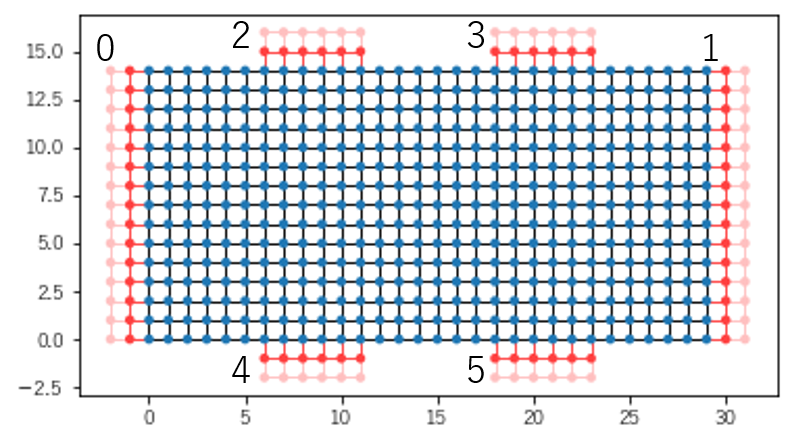
リードには手で番号を振っておきました。
ここからホール伝導度やホール抵抗などの値を計算していきます。基本となる関数はsmatrix.conductance_matrix()です。これを用いるとS行列から電流$I$と電圧$V$の間の比例関係$I=GV$の$G$を計算することができます。$I,V$は6本の端子のそれぞれに対して定義されるので、それぞれ$6$次元のベクトルになっており、したがって$G$は$6\times 6$行列です。端子0と1の間のみに電流を流した状態を$I_0=-I_1=I,\ \ I_2=I_3=I_4=I_5=0$とあらわすと、縦抵抗、ホール抵抗はそれぞれ$R_{long} = \frac{V_4-V_5}{I}, \ R_{Hall} = \frac{V_3-V_5}{I}$と書けるので、まずは行列$G$の逆行列を求めればよさそうです。
ところが、行列$G$は電流の保存則および電圧の原点の不定性から、ランク落ちしていることが知られています。よってここでは$V_5=0$を仮定し、$G$の右端の列を無視してしまいます。すると$G$は$6\times 5$行列となり、逆行列の問題は過剰決定となってしまいます。そこで一番下の行まで無視してしまって$G$を$5\times 5$行列として扱うことにします。
先述したパラメータphiはS行列を定義する際に辞書型で与えることができます(ここでの例ではphiを振る必要がなかったので外に出す必要はなかったのですが...。)
# S行列から縦抵抗、ホール抵抗、伝導度、ホール伝導度を求める関数。
from numpy.linalg import LinAlgError
def calc_conductances2(smatrix):
#コンダクタンス行列Gを計算
gmat = smatrix.conductance_matrix()
#行列がaccidentalにsingularになっている場合の例外処理
try:
Rmat = np.linalg.inv(gmat[:5,:5])
except LinAlgError:
R_long = np.nan
R_Hall = np.nan
sigma_xx = 0
sigma_xy = 0
else:
#V_5=0と置いたのでR_long=V_4/I
R_long = Rmat[4,0]-Rmat[4,1]
R_Hall = Rmat[3,0]-Rmat[3,1]
sigma_xx = R_long/(R_long**2+R_Hall**2)
sigma_xy =-R_Hall/(R_long**2+R_Hall**2)
return R_long , R_Hall , sigma_xx ,sigma_xy
phi=2*np.pi*1/11 #パラメータphiの値。
R_Halls =[]
R_longs =[]
sigma_xxs =[]
sigma_xys =[]
doss=[]
energies = np.linspace(-4,0,50)
for energy in energies:
#S行列の計算。パラメータを辞書型で与える。
smatrix = kwant.smatrix(syst, energy, params=dict(phi=phi) )
R_long, R_Hall, sigma_xx, sigma_xy = calc_conductances(smatrix)
R_Halls.append(R_Hall)
R_longs.append(R_long)
sigma_xxs.append(sigma_xx)
sigma_xys.append(sigma_xy)
#ついでに状態密度も計算。
dos = kwant.ldos(syst, energy, params=dict(phi=phi) ).mean()
doss.append(dos)
エネルギーの関数として伝導度、ホール伝導度をプロットしてみると
plt.plot(energies, doss, label="dos")
plt.plot(energies, sigma_xxs, label="sigma_xx")
plt.plot(energies, sigma_xys, label="sigma_xy")
plt.grid()
plt.ylim(-1,5)
plt.xlim(-4,-0.8)
plt.xlabel("energy/t")
plt.legend()
plt.show()
ホール伝導度が$e^2/h$の整数倍に量子化していること、状態密度と縦伝導度がランダウ準位っぽくなっていることが確認できます。
これで、オンサイトポテンシャルやホッピングを非一様にしたり、外からパラメータを与えたり、端子をたくさんつけたりできるようになりました。
おまけ(久保公式)
以下のコードで端子を付けることなく、久保公式を用いてより簡単にホール伝導度を計算できます。hopping関数のみを上から拝借していますが10行程度で計算できてしまいます。すごい!
W=100
L=W
t=1
a=1
lat = kwant.lattice.square(a)
syst = kwant.Builder()
syst[(lat(x, y) for x in range(L) for y in range(W))] = 0
syst[lat.neighbors()] = hopping
syst = syst.finalized()
sigma_xy = kwant.kpm.conductivity(syst, alpha='x', beta='y',params=dict(phi=2*np.pi/11))
conductivities = [sigma_xy(mu=mu, temperature=0)/L/W for mu in np.linspace(-4,0,50)]
plt.plot(np.linspace(-4,0,50),conductivities)
plt.grid()
ただし、デフォルトの設定のままだと量子化が甘く、計算精度に難があります。ここでの計算にはカーネル多項式法(KPM)を用いているらしく、細かく計算上のパラメータを調整することで精度を向上できます。デバイスサイズを大きくしてもいいですが、時間がめちゃかかります。この記事では著者の知識とやる気の限界のため詳細は本家のドキュメントに譲ります...。
おまけ(ゲージ)
なんと磁場を与えるとゲージ場とそれによるホッピングのPeierls位相をうまい事計算してくれる機能がv1.4で追加されていました。詳細はドキュメントを。
例3:異常量子ホール効果
最後の例としてHaldane model(の特別な場合)における異常量子ホール効果を見てみます。ハニカム格子状のスピンレスフェルミオンが純虚数次近接ホッピングをすると外部磁場なしでホール伝導度が量子化します。
これまでは正方格子を並べた長方形デバイスのみを考えていましたが、ここではハニカム格子を円形に並べたデバイスを作ってみます。まず格子形状を変えたものをlatとして定義します。簡単です。
# パラメータ
a=1
t=1.0
tt=0.5 #次近接ホッピング
L_lead=10
# ハニカム格子を定義。norbsはサイトあたり軌道の数を表すパラメータ(最後の電流分布以外はこれがなくても動く)。副格子にa,bと名付ける。
lat = kwant.lattice.honeycomb(a, norbs=1, name=['a', 'b'])
# ここは一緒
syst = kwant.Builder()
次にデバイスの形を定義してみます。形の定義には座標に対してbool値を返すような関数を使います。定義した形の内部の点を一つ指定することで、単連結な領域をサイトで埋め尽くすことができます。
# 形を定義
def circle(pos):
x, y = pos
return x**2 + y**2 < 100
# 形の内部の点を一つ指定。ここでは(0,0)。オンサイトポテンシャルは0
syst[lat.shape(circle, (0, 0))] = 0
ホッピングも同様に定義できます。副格子a,bを定義したのでその上だけでの最近接(=ハニカム格子の次近接)を簡単に指定できます。ここでは次近接ホッピングは純虚数とします。
syst[lat.neighbors()] = -t
syst[lat.a.neighbors()] = -1j*tt
syst[lat.b.neighbors()] = 1j*tt
リードの定義も同様です
lead = kwant.Builder(kwant.TranslationalSymmetry((-a, 0)))
def lead_shape(pos):
x, y = pos
return (-L_lead/2 < y < L_lead/2)
lead[lat.shape(lead_shape,(0,0))] = 0
lead[lat.neighbors()] = -t
lead[lat.a.neighbors()] = -1j*tt
lead[lat.b.neighbors()] = 1j*tt
syst.attach_lead(lead)
syst.attach_lead(lead.reversed())
デバイスの形を見てみましょう。
kwant.plot(syst)
syst = syst.finalized()
確かに円形のハニカム格子デバイスの両端にリードを付けることができました。よーく見ると次近接ホッピングを表す黒線も見えますね。リードは左右への半無限の並進対称性をうまいこと満たすようにつけてくれた結果少し変な形になっていますが、アームチェア方向とジグザグ方向でこの辺の形も変わりそうです。(試してません)
また端子を複数付けてホール伝導度の量子化を計算してみてもいいですが、せっかくなのでほかの方法で量子ホール状態を可視化してみます。まずは2端子間の透過率と状態密度を計算してみます。コードは例1とほぼ一緒です。
trans=[]
doss=[]
energies = np.linspace(-4,4,100,endpoint=False)
for energy in energies:
smatrix = kwant.smatrix(syst, energy )
trans.append(smatrix.transmission(0,1))
dos = kwant.ldos(syst,energy ).mean()
doss.append(dos)
plt.plot(energies, trans, label="conductance")
# 見栄えのため雑に10倍しています。
plt.plot(energies, [d*10 for d in doss], label="dos")
plt.grid()
plt.legend()
plt.xlabel("energy/t")
plt.show()
これを見ると、入射エネルギーが0付近の時にコンダクタンスが量子化していることがわかります。すなわち、散乱の無い伝導チャンネルが一本だけあることを表しています。
つぎに状態密度を見てみるとこのエネルギー領域で小さくなっています。状態密度の計算にはkwant.ldos()関数の空間平均を使いましたが、平均をとる前の実空間上での分布(局所状態密度)をプロットしてみましょう。
local_dos = kwant.ldos(syst,energy=0.1 )
kwant.plotter.map(syst,local_dos)
すると、状態密度はデバイスの端のみで有限になっていることがわかりますね。つまり電流はデバイスの端のみを流れることができ、内部の方は絶縁体的になっています。これは量子ホール状態に特有のエッジ状態によるエッジ伝導を表しています。
実際に電流の分布をプロットしてみることもできます。
psi = kwant.wave_function(syst,energy=0.1)(0)
J = kwant.operator.Current(syst)
current=sum(J(p) for p in psi)
kwant.plotter.current(syst,current,min_linewidth=.01,density=0.3)
リード0から入射された電子がどう流れているかをベクトル場的に表しています。確かにデバイスの端に局在したまま右端のリード1まで達していますね。
以上で変な形のデバイスや格子形状のデバイスを設計できることがわかりました。
まとめ
Kwantによる量子伝導計算を二次元系を中心に見てみました。まだ挙動の理解が出来ていない関数や、使いこなせていない機能がたくさんあり、ドキュメントを読み込んでいけばもっといろんな事が出来そうです。ドキュメントのほかにも議論用のメーリングリストやサンプルのjupyter notebookなどがKwantのホームページから探せますので、遊んでみてください。
ここで例示したもののほかにできそうな面白いこととして、
- スピン流、熱流の計算
- 周期系のバンド構造の計算
- 超伝導体、ジョセフソン接合?
- 局所ゼーマン磁場による静的な磁性との交換結合
- 3次元系、他の格子系
があります。時間とやる気があれば調べてみます。







