Rustでも格子探索を楽したい！

はじめに

本記事では競技プログラミングにおける格子探索系の問題で使えそうなライブラリについて紹介します。
筆者は AtCoder しか経験がないためほとんど 競プロ= AtCoder として本記事を執筆していますが、おそらくどのコンテストでも利用できるライブラリだと思います。
また、本記事ではライブラリの説明に実際の AtCoder の問題を挙げますのでネタバレもあります。ご了承ください。（最新の問題だと ABC246-E など）

格子探索問題って？

AtCoder では以下のような格子状のグリッドが与えられる格子探索問題がよく出題されます。
もっと広く知られた呼称があるのかもしれませんが、ひとまずこの記事では格子探索問題と称します。(そんなスタンスで見出しにしていいのか)(もっと相応しい呼称があればコメントしていただけると助かります。)

$H\ $ 行 $W$ 列の格子状の区画が与えられます。上から $i$ 行目、左から $j$ 列目の区画は、$S_{ij}$ が.のとき道、#のとき塀です。 高橋君がこの区画を上下左右に歩くので、（中略）を求めてください。

実際の問題ですと、
ABC213-E Stronger Takahashi
ABC246-E Bishop 2
ABC184-E Third Avenue
あたりでしょうか。

これらのような格子探索問題の場合、2 次元配列の座標を上下左右に動きたいことがよくあります。
競プロトップシェア、C++の提出コードを見に行くと以下のようなコードで上下左右の移動を実現しています。

int dx[4] = { -1, 0, 1, 0 };
int dy[4] = { 0, -1, 0, 1 };

// 現在 x, y にいるとして
for (int i = 0; i < 4; i++) {
    // 移動先が格子からはみ出ていなければ、
    if (0 <= x + dx[i] && x + dx[i] < h && 0 <= y + dy[i] && y + dy[i] < w) {
        // 上下左右に隣接する要素に対する処理をおこなう
        hoge(grid[x + dx[i]][y + dy[i]]);
    }
}

初めて見たときはdx・dyなる魔法の配列が表れてびっくりしましたが、手元で動かしてみるといい感じに上下左右に動けていることが確認できると思います。

Rust x 競プロで辛いこと

さて、この方法を Rust でもやってみると少し面倒なことになります。

let dx: [i32; 4] = [-1, 0, 1, 0];
let dy: [i32; 4] = [0, -1, 0, 1];

// 現在 x: usize, y: usize にいるとして
for i in 0..4 {
    let x: i32 = x as i32 + dx[i];
    let y: i32 = y as i32 + dy[i];
    if x <= 0 && x < h && y <= 0 && y < w {
        hoge(grid[x as usize][y as usize]);
    }
}

このような書き方になるのは以下の仕様があるためです。

• Rust では異なる型で（たとえ整数型同士でも）足し算が定義されていない
• 暗黙に型変換されない
• 配列の添え字は usize （およびその Range 系列）のみ受け付ける

3 つ目に関してはtrait Indexを魔改造しても良いかもしれませんね。
（あとでやります）

実現したいこと

一番実現したいことはこれです。

• ロジックを書きたいところに型変換や境界チェックを挟まない

また、以下のことにも気を使います。

• 汎用性・拡張性
• 自然な書き方

まあ色々言っててもしょうがないので実装と使用例を見ていただければと思います。

実装

実装は以下の通りです。
方針としてはIndexGeneratorに問題の状態を持たせます。

• グリッドの大きさhとw
• グリッドの移動を表すshift

そしてgenerate関数によって合法な格子座標を生成するIteratorを得ます。
Iteratorとすると嬉しい理由は使用例とともに説明します。

実装の詳細はstructに状態を持たせてIteratorを実装しているだけなのでコードを見ていただければと思います。

使用例を見た後に使えそうだと思ってもらえたら、また戻ってきてもらえればです。

struct IndexGenerator<'a> {
    h: usize,
    w: usize,
    shift: &'a [(i32, i32)],
}

impl<'a> IndexGenerator<'a> {
    fn new(h: usize, w: usize, shift: &'a [(i32, i32)]) -> Self {
        IndexGenerator { h, w, shift }
    }
    fn generate(&self, pos: (usize, usize)) -> ShiftedIndex {
        ShiftedIndex {
            cursor: 0,
            pos: (pos.0 as i32, pos.1 as i32),
            h: self.h as i32,
            w: self.w as i32,
            shift: self.shift,
        }
    }
}

struct ShiftedIndex<'a> {
    cursor: usize,
    pos: (i32, i32),
    h: i32,
    w: i32,
    shift: &'a [(i32, i32)],
}

impl<'a> Iterator for ShiftedIndex<'a> {
    type Item = (usize, usize);
    fn next(&mut self) -> Option<Self::Item> {
        while self.cursor < self.shift.len() {
            let (i, j) = (
                self.pos.0 + self.shift[self.cursor].0,
                self.pos.1 + self.shift[self.cursor].1,
            );
            self.cursor += 1;
            if 0 <= i && i < self.h && 0 <= j && j < self.w {
                return Some((i as usize, j as usize));
            }
        }
        None
    }
}

使用例

実装したIndexGeneratorを使用してABC213-E Stronger Takahashiを解いていきます。
（問題の解説も少し含みます。）

use itertools::Itertools;
use proconio::{input, marker::Chars};
use std::collections::VecDeque;

fn main() -> Result<(), Box<dyn std::error::Error>> {
    input! {
        h:usize,
        w:usize,
        s:[Chars; h],
    };
    let mut deque: VecDeque<(i64, usize, usize)> = VecDeque::new();
    deque.push_back((0, 0, 0));
    let mut grid = vec![vec![1 << 60; w]; h];
    grid[0][0] = 0;

    // (1)
    let adjacent = [(-1, 0), (0, -1), (1, 0), (0, 1)];
    let adjacent_index = IndexGenerator::new(h, w, &adjacent);

    // (2)
    let destroy = (-2..=2)
        .cartesian_product(-2..=2)
        .filter(|(i, j)| (*i != 0 || *j != 0) && i32::abs(*i * *j) != 4)
        .collect::<Vec<(i32, i32)>>();
    let destroy_index = IndexGenerator::new(h, w, &destroy);

    // (3)
    while let Some((cost, i, j)) = deque.pop_front() {
        if i == h - 1 && j == w - 1 {
            println!("{}", cost);
            return Ok(());
        }

        // (4)
        for (i, j) in adj_index.generate((i, j)) {
            if s[i][j] == '#' {
                continue;
            }
            if grid[i][j] > cost {
                grid[i][j] = cost;
                deque.push_front((cost, i, j));
            }
        }

        for (i, j) in destroy_index.generate((i, j)) {
            if grid[i][j] > cost + 1 {
                grid[i][j] = cost + 1;
                deque.push_back((cost + 1, i, j));
            }
        }
    }
    Ok(())
}

// ライブラリ部分は省略
// struct IndexGenerator ...

問題自体も水 diff で少し複雑ですがやっていることは公式解説と同じなのでロジックの解説は公式に丸投げします。

要は 01DFS です。

(1) 上下左右の移動

// (1)
let adjacent = [(-1, 0), (0, -1), (1, 0), (0, 1)];
let adjacent_index = IndexGenerator::new(h, w, &adjacent);

上下左右の移動を(i32, i32)の配列で持ち、それをIndexGeneratorの構造体に保持させます。

この時グリッドの大きさ(h、w)も渡しておきます。

(2) 破壊する壁も渡せる

// (2)
let destroy = (-2..=2)
    .cartesian_product(-2..=2)
    .filter(|(i, j)| (*i != 0 || *j != 0) && i32::abs(*i * *j) != 4)
    .collect::<Vec<(i32, i32)>>();
let destroy_index = IndexGenerator::new(h, w, &destroy);

IndexGeneratorは共有スライスとして移動量を保持するので動的に生成したVec<T>の参照でもnewを呼べます。
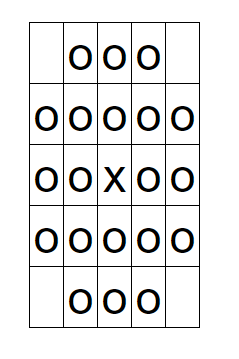
ここでは、以下のoで示したグリッドへの移動を生成しています。(xが現在位置)

(3) DFS ループ

// (3)
while let Some((cost, i, j)) = deque.pop_front() {
    if i == h - 1 && j == w - 1 {
        println!("{}", cost);
        return Ok(());
    }
    ...
}

01DFS なので前から要素を取っているだけです。
ここで、i、jはusizeで扱えていることに注目です。
移動を見越してi、jをi32で管理するなどといったテクも不要で、ロジックに集中できるのではないでしょうか。

(4) 現在のマスからの移動

// (4)
for (i, j) in adjacent_index.generate((i, j)) {
    if s[i][j] == '#' {
        continue;
    }
    if grid[i][j] > cost {
        grid[i][j] = cost;
        deque.push_front((cost, i, j));
    }
}

for (i, j) in destroy_index.generate((i, j)) {
    if grid[i][j] > cost + 1 {
        grid[i][j] = cost + 1;
        deque.push_back((cost + 1, i, j));
    }
}

ここが本記事で一番重要なところです。

なぜgenerateがIteratorを返すと嬉しいかというと、このようにfor ... inの後ろにgenerateを書けるようになります。

generateから返されたIteratorは現在の位置に対して合法な移動先のみを返すので、for文の中からロジックに関係のない 型変換や境界チェックを排除 できます。

これは実装すべきことをクリアにし、 問題の本質に集中できる ようになるとともに、タイプ数を減らすことで 実装時間の短縮 にも繋がります。

注意点

そのままでは使えない問題もあります。

• 方向を記録したい問題
  ABC246-E Bishop 2や競プロ典型 90 問 043 Maze Challenge with Lack of Sleepなどでは、上記の実装だと方向を別で管理しなくてはなりません。うまく実装し直せば使えると思うのでアレンジしてみてください。

まとめ

本記事では、Rustでも格子探索問題で楽したい！ということで移動を管理するライブラリを紹介しました。

今回は説明のために変数、構造体、関数にやや丁寧な名前を付けていますが、競技用にもっと短い名前に修正すれば、コード量も減らせることでしょう。

個人的にこのライブラリは気に入っていて、最初に例に挙げたC++の実装例よりも本番での実装部分については簡単になっているのではないでしょうか。

もし、「おっ、使えるかも？」と思っていただければ嬉しいです。

(最後になりますが、記事内での改善点、修正点などあれば指摘していただけると幸いです。)

以下は余談です。

もっと便利に？

std::ops::{Index, IndexMut}を使用します。
これを用いると二次元配列に対しても 1 つの[]でアクセスできるようになります。
前章でfor (i, j) in ...のように分割代入していた所もすっきり書けます。
今回はライブラリ全体も省略せずお見せします。

use itertools::Itertools;
use proconio::{input, marker::Chars};
use std::collections::VecDeque;

fn main() -> Result<(), Box<dyn std::error::Error>> {
    input! {
        h:usize,
        w:usize,
        s:[Chars; h],
    };
    let mut deque: VecDeque<(i64, Position)> = VecDeque::new();
    deque.push_back((0, Position(0, 0)));
    let mut grid = vec![vec![1 << 60; w]; h];
    grid[0][0] = 0;

    let limit = Position(h, w);
    let goal = Position(h - 1, w - 1);

    let adjacent = [(-1, 0), (0, -1), (1, 0), (0, 1)];
    let adjacent_index = IndexGenerator::new(limit, &adjacent);
    let destroy = (-2..=2)
        .cartesian_product(-2..=2)
        .filter(|(i, j)| (*i != 0 || *j != 0) && i32::abs(*i * *j) != 4)
        .collect::<Vec<(i32, i32)>>();
    let destroy_index = IndexGenerator::new(limit, &destroy);

    while let Some((cost, pos)) = deque.pop_front() {
        if pos == goal {
            println!("{}", cost);
            return Ok(());
        }
        for pos in adjacent_index.generate(pos) {
            if s[pos] == '#' {
                continue;
            }
            if grid[pos] > cost {
                grid[pos] = cost;
                deque.push_front((cost, pos));
            }
        }
        for pos in destroy_index.generate(pos) {
            if grid[pos] > cost + 1 {
                grid[pos] = cost + 1;
                deque.push_back((cost + 1, pos));
            }
        }
    }
    Ok(())
}

struct IndexGenerator<'a> {
    limit: Position,
    shift: &'a [(i32, i32)],
}

impl<'a> IndexGenerator<'a> {
    fn new(limit: Position, shift: &'a [(i32, i32)]) -> Self {
        IndexGenerator { limit, shift }
    }
    fn generate(&self, pos: Position) -> ShiftedIndex {
        ShiftedIndex {
            cursor: 0,
            pos: (pos.0 as i32, pos.1 as i32),
            limit: (self.limit.0 as i32, self.limit.1 as i32),
            shift: self.shift,
        }
    }
}

struct ShiftedIndex<'a> {
    cursor: usize,
    pos: (i32, i32),
    limit: (i32, i32),
    shift: &'a [(i32, i32)],
}

impl<'a> Iterator for ShiftedIndex<'a> {
    type Item = Position;
    fn next(&mut self) -> Option<Self::Item> {
        while self.cursor < self.shift.len() {
            let (i, j) = (
                self.pos.0 + self.shift[self.cursor].0,
                self.pos.1 + self.shift[self.cursor].1,
            );
            self.cursor += 1;
            if 0 <= i && i < self.limit.0 && 0 <= j && j < self.limit.1 {
                return Some(Position(i as usize, j as usize));
            }
        }
        None
    }
}

#[derive(PartialEq, Clone, Copy)]
struct Position(usize, usize);

use std::ops::{Index, IndexMut};
impl<T> Index<Position> for Vec<Vec<T>> {
    type Output = T;
    fn index(&self, index: Position) -> &Self::Output {
        &self[index.0][index.1]
    }
}

impl<T> IndexMut<Position> for Vec<Vec<T>> {
    fn index_mut(&mut self, index: Position) -> &mut Self::Output {
        &mut self[index.0][index.1]
    }
}

できそうだからやってみましたが、個人的にstd::ops::{Index, IndexMut}はやりすぎな気もしてきたので()、もし興味があれば使ってみてください。
一応、While let Some() = ... { ... }の DFS ループ内で分割代入を回避しているのが確認できると思います。