LoginSignup
1
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@jirojiro

非情報系大学院生が一から機械学習を勉強してみた #2：ニューラルネットワーク

Posted at

#はじめに
非情報系大学院生が一から機械学習を勉強してみました。勉強したことを記録として残すために記事に書きます。
進め方はやりながら決めますがとりあえずは有名な「ゼロから作るDeep-Learning」をなぞりながら基礎から徐々にステップアップしていこうと思います。環境はGoogle Colabで動かしていきます。第2回はニューラルネットワークです。

#目次

  1. 活性化関数
  2. 出力層の活性化関数
  3. 実際にニューラルネットワークを組んでみる

#1. 活性化関数
第1回ではバイアス付きパーセプトロンの出力を以下のように表現しました。
$$
y = \begin{cases}
0 & (w_1x_1+w_2x_2+b \leq 0) \
1 & (w_1x_1+w_2x_2+b > 0)
\end{cases}
$$
これを関数$h(x)$を導入することで単純かつ一般的に拡張します。
$$
y = h(a) = \begin{cases}
0 & (a \leq 0) \
1 & (a > 0),
\end{cases} \
a = w_1x_1+w_2x_2+b \
$$
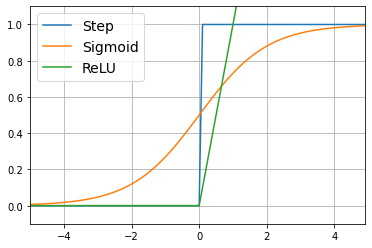
この$h(x)$のことを活性化関数と呼びます。名前の通り関数がどのように活性化（発火）するのかを決めています。なお、上の式では第1回でも用いた原点で0、1が不連続的に変化する関数を用いた例です。一般に活性化関数に用いられる関数をいくつか紹介していきます。

###ステップ関数
これまで説明してきた入力が0を超えるか超えないかで出力が切り替わる関数をステップ関数と呼びます。つまり

$$
h(x) = \begin{cases}
0 & (x \leq 0) \
1 & (x > 0)
\end{cases}
$$
で表されます。

Step関数
def step_function(x):
    return np.array(x > 0, dtype=np.int)

###Sigmoid関数
Sigmoid関数はニューラルネットワークに最もよく使われる活性化関数の一つで以下の式で表されます。

$$
h(x) = \frac{1}{1+\exp(-x)}
$$

ステップ関数と比べてみると、ステップ関数が不連続関数だっただめ$x=0$で微分不可能になってしまいます。また、微分値は$x=0$を除き常に0であり変化なしということになってしまいます（実際は不連続に値が変化しているがそれが表現できていない）。一方、Sigmoid関数では同じように入力が小さいと出力は0になり（近づき）大きいと1になる（近づく）という性質がありますが、連続関数であるため微分可能で、0、1の境の値も連続的に用いることができます。これらの特徴からニューラルネットワークの活性化関数にはステップ関数ではなくSigmoid関数が用いられます。

Sigmoid関数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

###ReLU関数
ReLU関数は最近のニューラルネットワークでよく用いられるようになった活性化関数で以下の式で表されます。

$$
h(x) = \begin{cases}
x & (x > 0) \
0 & (x \leq 0)
\end{cases}
$$

ReLU関数はステップ、Sigmoid関数に比べて処理が単純で学習が早く進み、かつ性能も良いと言われています。また、古典的にニューラルネットワークで良く用いられたSigmoid関数に比べて勾配消失問題（たぶん後で出てくる）が起こりにくく、微分も一応は可能1などの点から現在広く用いられています。

ReLU関数
def relu(x):
    return np.maximum(0, x)

activation_fun.png

#2. 出力層の活性化関数
ニューラルネットワークは前回の最後で登場した多層パーセプトロン（Multi Layer Perceptron: MLP）がベースとなっています。前章で見てきた活性化関数はニューラルネットワークの中でも内部の隠れ層で用いられます。終段の層は特別で別の活性化関数$\sigma$がよく用いられます。
ニューラルネットワークは回帰問題、分類問題ともに利用できますが、解く問題によって出力層の設計が異なります。

###回帰問題
入力データから（連続的な）数値の予測を行う回帰問題では出力層の活性化関数として恒等関数が用いられます。恒等関数とは名前の通りそのままの値を出力するということです。すなわち

$$
x \rightarrow \sigma(x) \rightarrow x
$$

となります。

###分類問題
入力データをいくつかのクラスに分類する分類問題では出力層の活性化関数としてSoftmax関数が用いられます。Softmax関数は以下のように表されます。

$$
y_k = \frac{\exp(a_k)}{\displaystyle\sum_{i=1}^n\exp(a_i)}
$$

分母がすべての和、分子がそのうちの一つとなっているのでこの式は$a_i$のうちある$a_k$をとる確率と見ることができます。つまり入力データがそれぞれのクラスに分類される確率を求めて一番高いクラスに分類する、というイメージとして解釈できます。ちなみに実装上はオーバーフロー対策のため以下の等価関数を用います。

$$
y_k = \frac{\exp(a_k-C)}{\displaystyle\sum_{i=1}^n\exp(a_i-C)}, C=\max{a_i}
$$

Softmax関数は指数の計算なので分子分母に同じ定数を乗除しても加減に変換されて結果は変わらないことを利用しています。

#3. 実際にニューラルネットワークを組んでみる
ニューラルネットワークを実装する準備ができたので実装してみます。ここでは下図のような3層ニューラルネットワークを考えます。まさしくMLPとそっくりです。
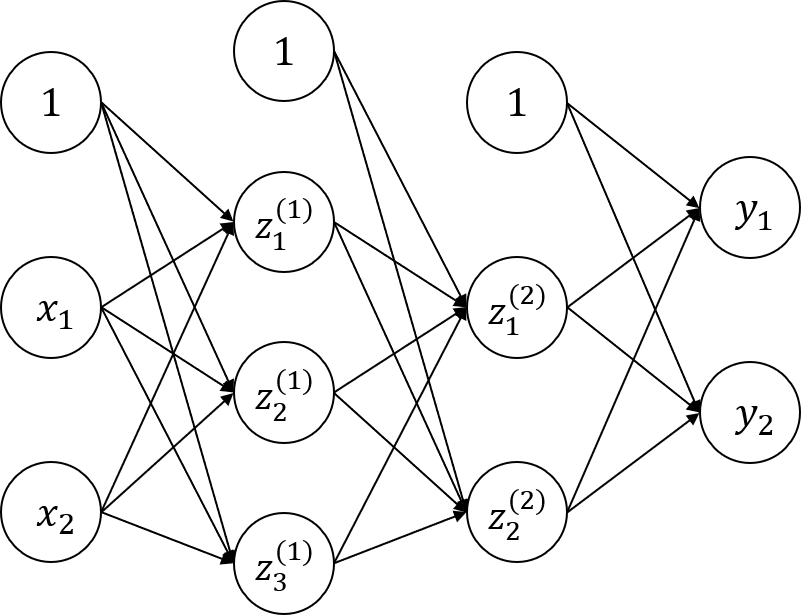
network.png
内部の動きを考えるためにここでは第0層（入力層）から第1層への伝搬を説明していきます。ここで$x_n, a_m^{(k)}, z_m^{(k)}, b_m, w_{m,n}, y_l$はそれぞれ$n$番目の初期入力、第$k$層$m$番目ニューロンの入出力、$m$番目ニューロンへのバイアス、$n$番目出力から$m$番目入力への重み、$l$番目の最終出力とします。
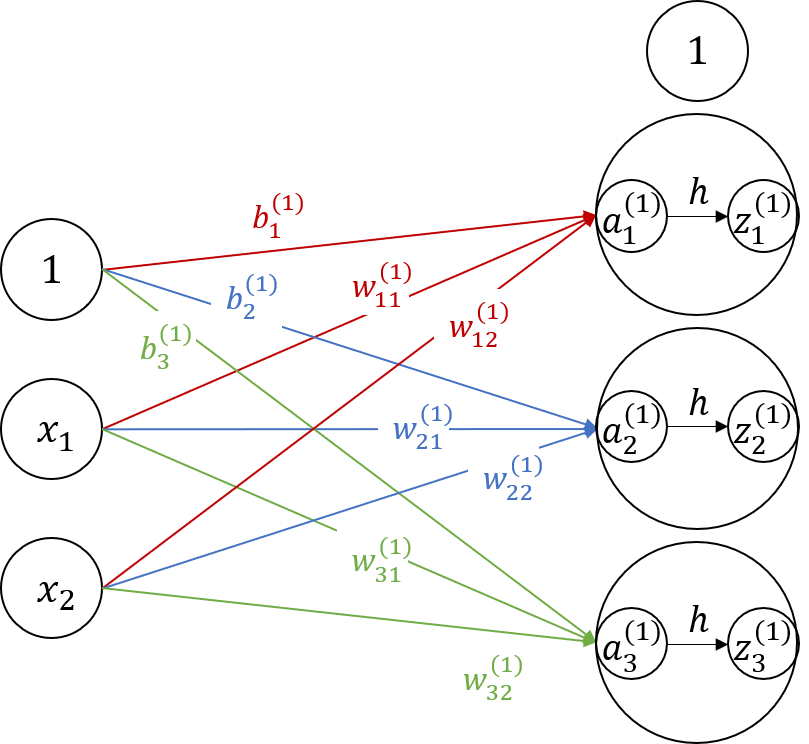
01network.png
第1層への入力は
$$
\color{Crimson}{a_1^{(1)} = w_{11}^{(1)}x_1 + w_{12}^{(1)}x_2 + b_1^{(1)}},\
\color{RoyalBlue}{a_2^{(1)} = w_{21}^{(1)}x_1 + w_{22}^{(1)}x_2 + b_2^{(1)}},\
\color{ForestGreen}{a_3^{(1)} = w_{31}^{(1)}x_1 + w_{32}^{(1)}x_2 + b_3^{(1)}}
$$
となります。
これを行列表記に直すと
$$
\boldsymbol{A}^{(1)} = \boldsymbol{XW}^{(1)} + \boldsymbol{B}^{(1)}, \
\boldsymbol{A}^{(1)} = \left[a_1^{(1)}~a_2^{(2)}~a_3^{(1)}\right], \
\boldsymbol{X} = \left[x_1^{(1)}~x_2^{(2)}\right], \
\boldsymbol{W}^{(1)} = \left[
\begin{array}{rrr}
w_{11} ^{(1)} & w_{21}^{(1)} & w_{31}^{(1)}\
w_{12} ^{(1)} & w_{22}^{(1)} & w_{32}^{(1)}
\end{array}
\right], \
\boldsymbol{B}^{(1)} = \left[b_1^{(1)}~b_2^{(2)}~b_3^{(1)}\right]
$$
となります。（個人的には$w_{m,n}$をこのように定義するなら全て転置した行列で書いた方が要素がきれいな気がしますが本に合わせてこのままいきます。）
第1層への入力$\boldsymbol{A}^{(1)}$は活性化関数$h$を通って第1層出力$\boldsymbol{Z}^{(1)}$に変換されます。
$$
\boldsymbol{Z}^{(1)} = h\left(\boldsymbol{A}^{(1)}\right),\
\boldsymbol{Z}^{(1)} = \left[z_1^{(1)}~z_2^{(2)}~z_3^{(1)}\right]
$$
あとは同様に第1→2層、第2→3層と計算しますが、出力層は活性化関数が異なるので出力層のみ以下のようになります。
$$
\boldsymbol{Y} = \sigma\left(\boldsymbol{A}^{(3)}\right),\
\boldsymbol{Y} = \left[y_1~y_2~y_3\right]
$$
ここまでの式をプログラムで実装します。

3層ニューラルネットワーク
def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([[0.1, 0.2, 0.3]])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([[0.1, 0.2]])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([[0.1, 0.2]])

    return network

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = a3

    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)    #[[0.31682708 0.69627909]]

はじめのinit_network()関数で各層の重み、バイアスの値を定義しています。次のforward()関数でネットワーク内の行列計算を表現しています。メインコードでは重み、バイアスと入力xをforward関数に与えて出力yを計算させます。

これでニューラルネットワークの実装ができました。次回はニューラルネットワークの使用例としてMNIST手書き数字認識問題をやってみます。

#参考文献
ゼロから作るDeep-Learning
ゼロから作るDeep-Learning GitHub
深層学習 (機械学習プロフェッショナルシリーズ)

  1. 厳密にはReLU関数も数学的に$x=0$で微分不可能ですが、プログラム的には$dh/dx=1~(x>0),~0~(x\leq0)$と表現でき、Sigmoid関数と違って一応変化があったことは表現できているので良いそう。 ↩

1
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?