はじめに
非情報系大学院生が一から機械学習を勉強してみました。勉強したことを記録として残すために記事に書きます。
進め方はやりながら決めますがとりあえずは有名な「ゼロから作るDeep-Learning」をなぞりながら基礎から徐々にステップアップしていこうと思います。環境はGoogle Colabで動かしていきます。第7回はこれまで取り組んできたニューラルネットワークを元に畳み込みニューラルネットワーク(CNN:Convolutional Neural Network)を実装します。
目次
- 畳み込みニューラルネットワークとは
- 畳み込み層
- プーリング層
- CNNの実装
1. 畳み込みニューラルネットワーク(CNN)とは
畳み込みニューラルネットワーク(CNN)とは脳の視覚野をモデルとして後述する畳み込み演算とプーリング演算を用いたニューラルネットワークのことです。
これまでの全結合ニューラルネットワークと同様ブロック図で以下のように表すことができます。

なぜ畳み込みニューラルネットワークが良いのか
CNNは画像の認識に特に優れています。例としてこれまで見てきたMNIST手書き数字認識問題を考えます。これまでの全結合のニューラルネットワークでは28ピクセル×28ピクセルだった元の画像データを1×784のベクトルに変形して学習していました。しかしながら、本来画像のピクセルデータの並び方には意味があるはずです。例えば隣接ピクセル同士は徐々に濃度が変化しているはずです。これを表現するためには列ベクトルに変換せずに元の28×28の状態で学習を行わなくてはいけません。CNNではこのような入力を得意としているので、データをうまく理解できる可能性が高くなります。
2. 畳み込み層
畳み込み演算とは
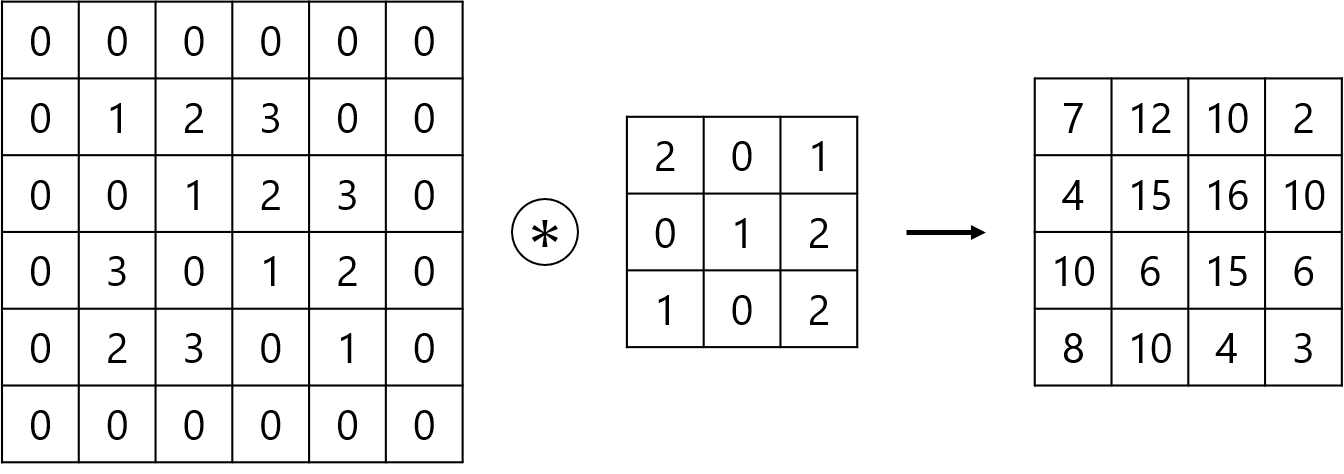
まず畳み込み層の動作である畳み込み演算について以下の例を見ていくことにします。真ん中の記号は畳み込み演算を表します。




畳み込み演算では入力データに対してフィルタのウインドウを一定の間隔でスライドさせながら適用していきます。このスライドさせていく一定の幅をストライドと呼びます。上の図はストライドが1のときの例です。まず青の領域で畳み込みを行い
$$
1×2+2×0+3×1+0×0+1×1+2×2+3×1+0×0+1×2=15
$$
というように計算していきます。ウインドウをスライドさせながら赤、黄、緑の領域も同様に計算していきます。あとはすべての結果にバイアスを加算して畳み込み演算の出力になります。
パディング
今の例で見たように畳み込み演算を行うと出力のサイズが小さくなってしまいます。そうではなく出力も同じサイズで行いたいときがあります。その場合入力データの周囲に固定のデータ(例えば0)を埋めることがあります。これをパディングといい、畳み込み演算ではよく行われます。こうすることで出力データを元のサイズと同じにすることができます。下の図は周囲に0をパディングしたときの例です。
3次元の畳み込み
これまではMNIST問題のようにグレースケール2次元画像を念頭に行ってきました。一般に画像データはR,G,Bの3色の要素があります。このように複数チャネルのデータがあるときもチャネルを3次元目として同様に畳み込み演算を行うことができます。3次元の畳み込みでは、まずチャネルごとに入力データとフィルタの畳み込み演算を行い、最後にそれらの結果を加算して1つの出力を得ます。
3. プーリング層
プーリングは縦・横方向の空間を小さくする演算です。例えば下図のように2×2の領域を1つの要素に集約するような処理を行い、空間サイズを小さくします。

図では2×2の領域から最大値を取る演算をしています。この処理をMax-Poolingといいます。最大値をとるのではなく平均値をとるものもあり、こちらはAverage-Poolingと呼びますが、画像認識では主にMax-Poolingが使われるため、以降では単にプーリングというとMax-Poolingを指すものとします。プーリング演算では通常ウインドウサイズとストライドは同じ値に設定します。
プーリング層は対象領域から最大値を取るだけなので学習パラメータが存在しない、演算はチャネルごとに行われるためチャネル数は変化しない、といった特徴があります。
また、プーリング演算は入力データの小さなズレ(ウインドウ内で多少値の変動があっても)に対してロバストという性質もあります。これは入力データの小さなズレを吸収してくれることになります。
4. CNNの実装
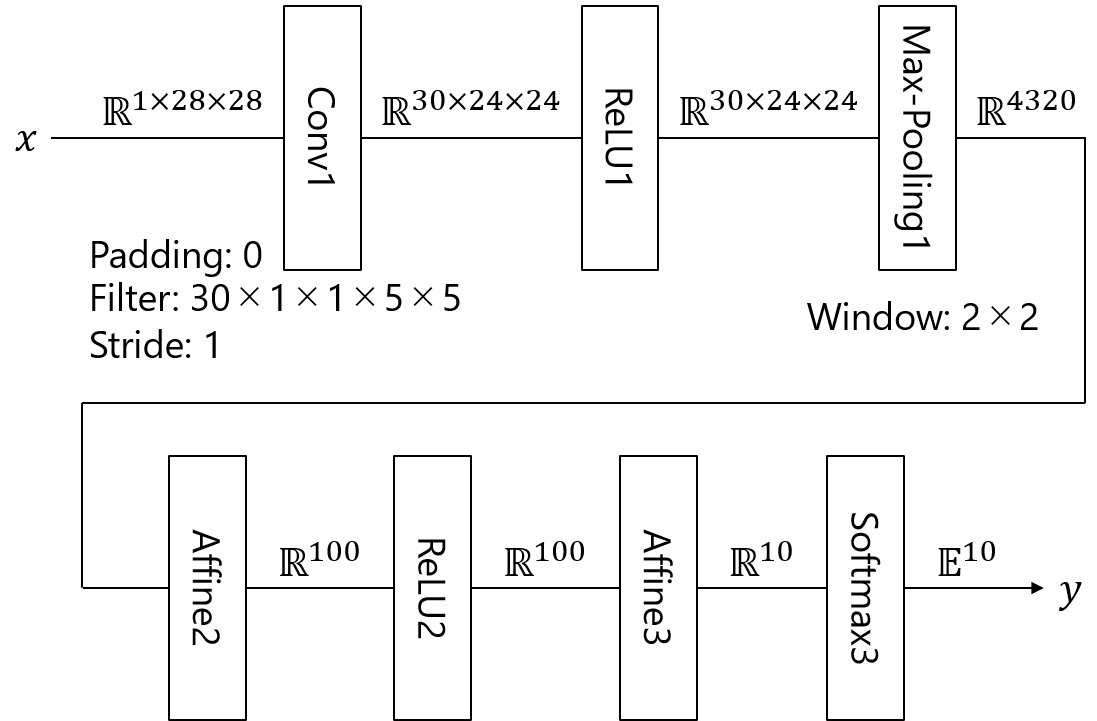
CNNの理論を簡単にまとめたところで実装を行っていきます。今回は以下のような構造のネットワークをChainerを用いてGPUを使った実装をしていきます。
import numpy as np
import matplotlib.pyplot as plt
import chainer
from chainer import Variable
from chainer import functions as F
from chainer import links as L
- chainer: chainerメインモジュール
- chainer.Variable: 誤差逆伝播法による勾配計算の対象となる変数クラス
- chainer.functions: 誤差逆伝播法と関係のない関数群
- chainer.links: 誤差逆伝播法と関係のある関数群
です。
class CNN(chainer.Chain):
# Constructor
def __init__(self, initializer = None):
super().__init__(
Conv1 = L.Convolution2D(1, 30, ksize=(5, 5), stride=1, pad=0),
Affine2 = L.Linear(4320, 100, nobias=False, initialW=initializer),
Affine3 = L.Linear(100, 10, initialW = initializer),
)
# Forward operation
def __call__(self, x, t = None):
z1 = F.relu(self.Conv1(x)) # Conv1 - ReLU1
pool1 = F.max_pooling_2d(z1, ksize=(2, 2)) #Max-Pooling1
z2 = F.relu(self.Affine2(pool1)) # Affine2 - ReLU2
a3 = self.Affine3(z2) # Affine3
if chainer.config.train:
return F.softmax_cross_entropy(a3, t) # Softmax3 with cross entropy error, training
else:
return F.softmax(a3) # Softmax3, evaluation
return a3
ここでニューラルネットワークのモデルを定義し学習を行います。上の図の通りの層順で計算していきます。学習パラメータを持つConvolution層、Affine層をコンストラクタで定義し、それ以外のReLU層、Max-pooling層、Softmax層をcallメゾットとして定義します。
L.Convolution2Dの主なパラメータは
chainer.links.Convolution2D(入力チャネル数, 出力チャネル数, フィルタサイズ(カーネル), ストライド数, パディング数, バイアスの有無, 初期重み, 初期バイアス)
です。
L.Linearの主なパラメータは
chainer.links.Linear(入力ベクトル数, 出力ベクトル数, バイアスの有無, 初期重み, 初期バイアス)
です。
# Load datasets
train, test = chainer.datasets.get_mnist(ndim = 3)
x_train = train._datasets[0] # (60000, 1, 28, 28)
t_train = train._datasets[1] # (60000,)
x_test = test._datasets[0] # (10000, 1, 28, 28)
t_test = test._datasets[1] # (10000,)
# Set GPU
gpu_device = 0 # 使用するGPUの指定
chainer.cuda.get_device(gpu_device).use()
# Model transfer to GPU
model = CNN(initializer = chainer.initializers.HeNormal())
model.to_gpu(gpu_device)
# Set optimizer engine
optimizer = chainer.optimizers.Adam()
optimizer.use_cleargrads()
optimizer.setup(model)
GPUが使えるように設定していきます。gpu_deviceで使用するGPUを指定します。
続いて先ほど定義したCNNモデルをGPUへ転送します。ここでinitializerで初期重みとして前回説明したHeの初期値を用います。
次にoptimizersで最適化エンジンを指定します。こちらも前回整理した最適化手法から今回はAdamを選択しました。これで学習を行う準備が整いました。
iters_num = 10000 # 最大イタレーション数
train_size = x_train.shape[0] # 訓練データ数
test_size = x_test.shape[0] #テストデータ数
batch_size = 100 # バッチサイズ
iter_per_epoch = max(train_size / batch_size, 1) #1エポックに要するイテレーション数
train_acc_list = []
test_acc_list = []
ここからは学習を行います。まずパラメータを設定、初期化します。
for i in range(iters_num):
# Set mini-batch
batch_mask = np.random.choice(train_size, batch_size)
x_batch = chainer.cuda.to_gpu(x_train[batch_mask], device = gpu_device)
t_batch = chainer.cuda.to_gpu(t_train[batch_mask], device = gpu_device)
# Forward operation
loss = model(x_batch, t_batch)
# Backward operation
model.cleargrads()
loss.backward()
# Update parameters
optimizer.update()
batch_size個のデータをランダムに抽出しミニバッチを作成します。ミニバッチごとにデータを転送します。
続いて順伝播演算を行い損失関数を計算、逆伝播演算を行い勾配を計算します。
その結果に基づきCNNの重み、バイアスバラメータを更新します。
# Evaluation
if i % iter_per_epoch == 0 or i == iters_num - 1:
# Turn training flag off
chainer.config.train = False
# Evaluate training set
y_train = []
for s in range(0, train_size, batch_size):
x_batch = chainer.cuda.to_gpu(x_train[s:s + batch_size])
y_train.extend(chainer.cuda.to_cpu(model(x_batch).data).tolist())
# Evaluate test set
y_test = []
for s in range(0, test_size, batch_size):
x_batch = chainer.cuda.to_gpu(x_test[s:s + batch_size])
y_test.extend(chainer.cuda.to_cpu(model(x_batch).data).tolist())
# Compute accuracy
train_acc = F.accuracy(np.array(y_train), t_train).data
test_acc = F.accuracy(np.array(y_test), t_test).data
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
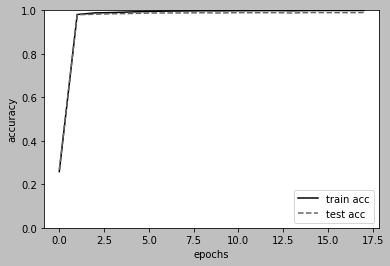
print(i, train_acc, test_acc) # 9999 0.9995166666666667 0.9899
# Turn training flag on
chainer.config.train = True
# Plot figure
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()
はじめにchainer.config.trainをFalseにしてCNNモデルの定義の学習モードと評価モードを切り替えます。
訓練データについて、
-
x_batchとしてバッチサイズごとに入力データをGPUに転送する。 -
model(x_batch)で訓練データに対するラベルを予測する。 - 予測した結果を
chainer.cuda.to_cpuでCPUに転送する。 - リスト型に変換し、その予測結果を
extend()でリストに追加する。
テストデータに対しても同様に行います。
chainer.functions.accuracy関数を用いて精度を計算します。これまでべた書きしていたものを関数を使っただけです。
最後に結果をプロットします。printした数値出力とプロット結果から学習終了時で訓練データに対して99.95%、テストデータに対して98.99%の正答率が得られました。
参考文献
ゼロから作るDeep-Learning
ゼロから作るDeep-Learning GitHub
深層学習 (機械学習プロフェッショナルシリーズ)