はじめに
非情報系大学院生が一から機械学習を勉強してみました。勉強したことを記録として残すために記事に書きます。
進め方はやりながら決めますがとりあえずは有名な「ゼロから作るDeep-Learning」をなぞりながら基礎から徐々にステップアップしていこうと思います。環境はGoogle Colabで動かしていきます。初回はニューラルネットワークの基礎、パーセプトロンです。
目次
- パーセプトロンとは
- パーセプトロンによる論理回路
- パーセプトロンの限界
- 多層パーセプトロン(MLP)
1. パーセプトロンとは
人間の脳内はニューロンと呼ばれる細胞が発火し次々と信号を伝えています。ニューラルネットワークとはこのニューロンの働きを模倣したシステムで、1つ1つのニューロンの働きをするものをパーセプトロン(人口ニューロン、単純パーセプトロンともいう)といいます。
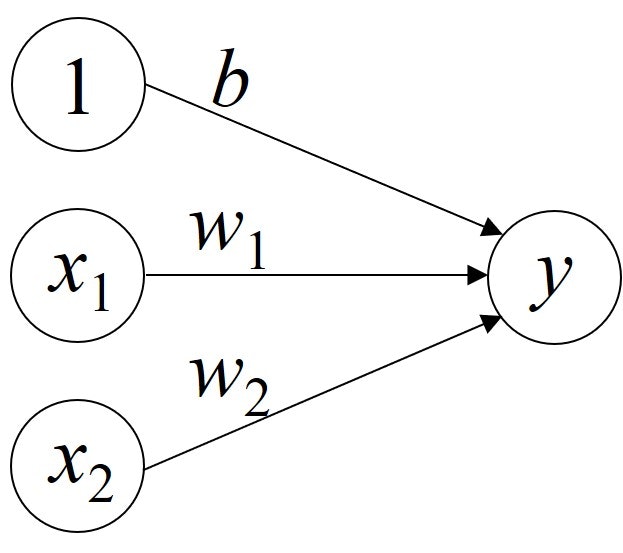
2入力$x_1, x_2$のシステムを考えると、それぞれの入力に重み$w_1, w_2$をかけたものの和があるしきい値$\theta$を超えたとき1を出力します。つまり以下のようになります。
$$
y = \begin{cases}
0 & (w_1x_1+w_2x_2 \leq \theta) \
1 & (w_1x_1+w_2x_2 > \theta)
\end{cases}
$$
以降のことを考えて一般に用いられるバイアス項$b$を加えた表記に直しておきます。
$$
y = \begin{cases}
0 & (w_1x_1+w_2x_2+b \leq 0) \
1 & (w_1x_1+w_2x_2+b > 0)
\end{cases}
$$
パーセプトロンでは入力に重みをかけた値とバイアスの和が0を超えたとき1を出力し(発火)、そうでなければ1を出力します。
2. パーセプトロンによる論理回路
パーセプトロンを用いてANDゲートを実装します。AND回路は以下のような真理値表で表されるゲートです。
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
バイアス付きの式を素直に実装します。
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2]) #入力
w = np.array([0.5, 0.5]) #重み
b = -0.7 #バイアス
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
入力とバイアスを例えば以下のように変更してあげるとORゲートやNANDゲートも実装することができます。これらの変更はパーセプトロンにおいて重み、バイアスを調整することで同じシステムでAND,OR,NANDゲートを作ることができることを意味します。
# ORゲート
w = np.array([0.5, 0.5])
b = -0.2
# NANDゲート
w = np.array([-0.5, -0.5])
b = 0.7
3. パーセプトロンの限界
ではパーセプトロンを用いればどんな論理回路も実装できるのでしょうか?いえ、決してそんなことはありません。例にXORゲートの実装を考えます。XORゲート(排他的論理和)は以下の真理値表で表されます。
| $x_1$ | $x_2$ | $y$ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
実はこの真理値表はどう頑張ってもパーセプトロン(単層パーセプトロン)では実装できません。その理由を考えるために線形分離可能性を考えます。上の例に挙げた重み、バイアスの値を代入すると
$$
\begin{cases}
x_2 = -x_1 + 1.4 & (\text{ANDゲート}) \
x_2 = -x_1 + 0.4 & (\text{ORゲート})
\end{cases}
$$
となります(NANDはANDゲートを反転させただけなので省略)。これらをグラフに図示するとこのようになります。

そうです、ANDとORゲートでは0の領域と1の領域を線形に分離することができます。ではXORゲートではどうなるでしょうか?
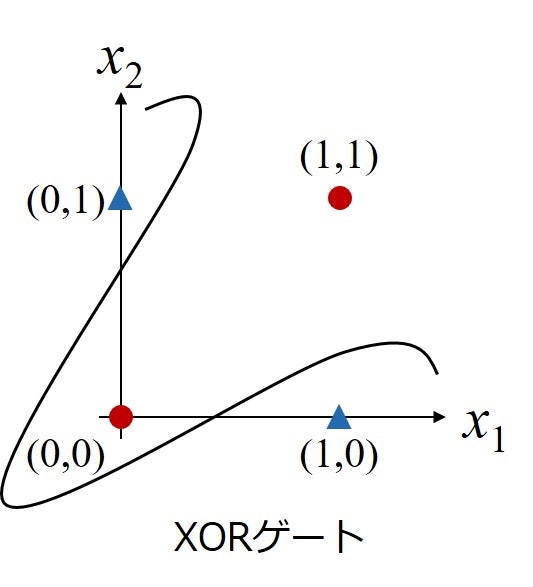
XORゲートでは0と1の領域を直線で分離することができません。つまりパーセプトロンで表現できるのは線形分離可能なものに限ります。
4. 多層パーセプトロン(MLP)
前節で述べたように単層パーセプトロンではXORゲートを表現できません。しかしパーセプトロンの良いところは層を重ねることができることです。複数のパーセプトロンを層として重ねたものを多層パーセプトロン(Multi Layer Perceptron: MLP)と呼びます。MLPを用いればAND, OR, NANDゲートの組み合わせとしてXORゲートをつくることができます。NANDの出力を$s_1$, ORの出力を$s_2$とするとXOR出力$y$は$s_1$と$s_2$のANDをとったものとして表現できます。すなわち以下の真理値表で表されます。
| $x_1$ | $x_2$ | $s_1$ | $s_2$ | $y$ |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 |
以上を踏まえて実装していきます。ここで上で定義したAND, OR, NAND関数を用いました。
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
# XOR(0,0) --> 0
# XOR(0,1) --> 1
# XOR(1,0) --> 1
# XOR(1,1) --> 0
このように入力層を0層とカウントするとNAND, ORで構成される第1層とANDによる第2層の2層MLPでXORゲートを実装できました(普通はこれを3層でなく2層というらしい)。
MLPは次回まとめるニューラルネットワークにも関わるのでそちらで改めて出てくると思います。