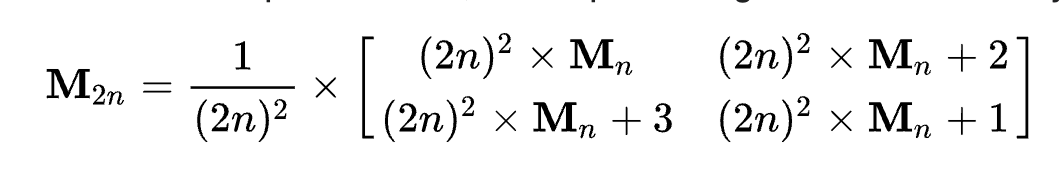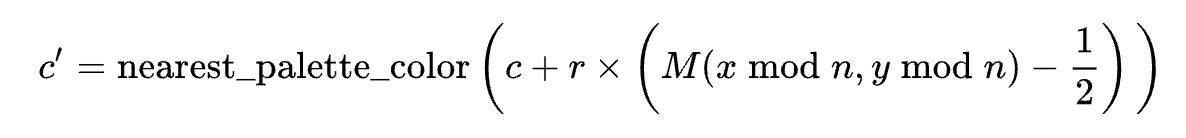本記事はHoudini Advent Calendar 2022の19日目の記事となります。
Houdiniでピクセルアートを作る(Ordered Dithering利用編)
Ordered Dithering
今年は軽いアルゴリズミック・デザイン的なトピックとして、Houdiniを使って2Dピクセルアートを作る方法を書いてみたいと思います。単純にピクセルアートといっても、今回取り扱うのは色数が限定されていてグラデーションを少ない数の色で表現する手法について取り扱います。具体的には Ordered Dithering という簡単なディザリングのアルゴリズムを使って実装していきます。基本的にはWikipediaに載っている方法をそのまま実装する感じです。
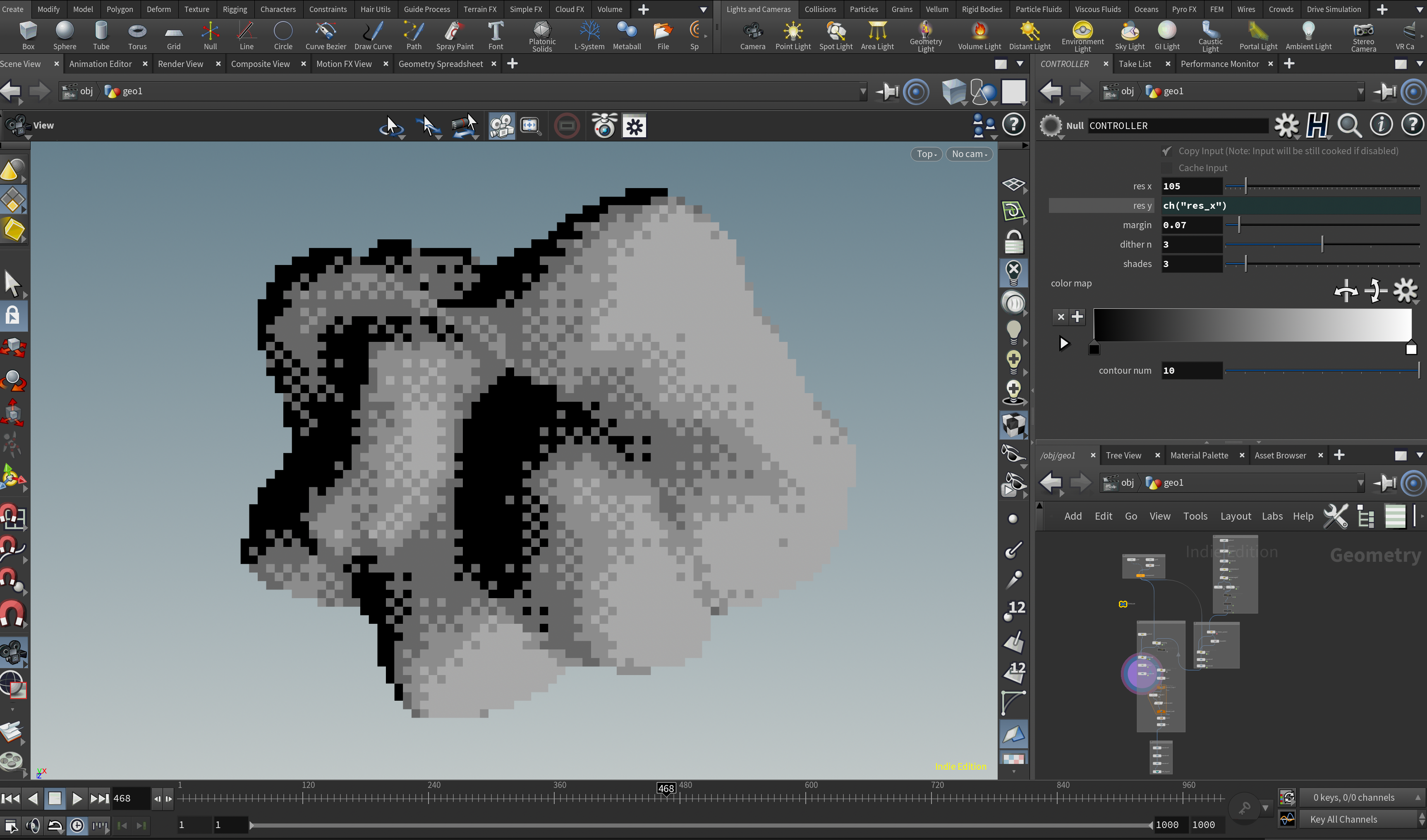
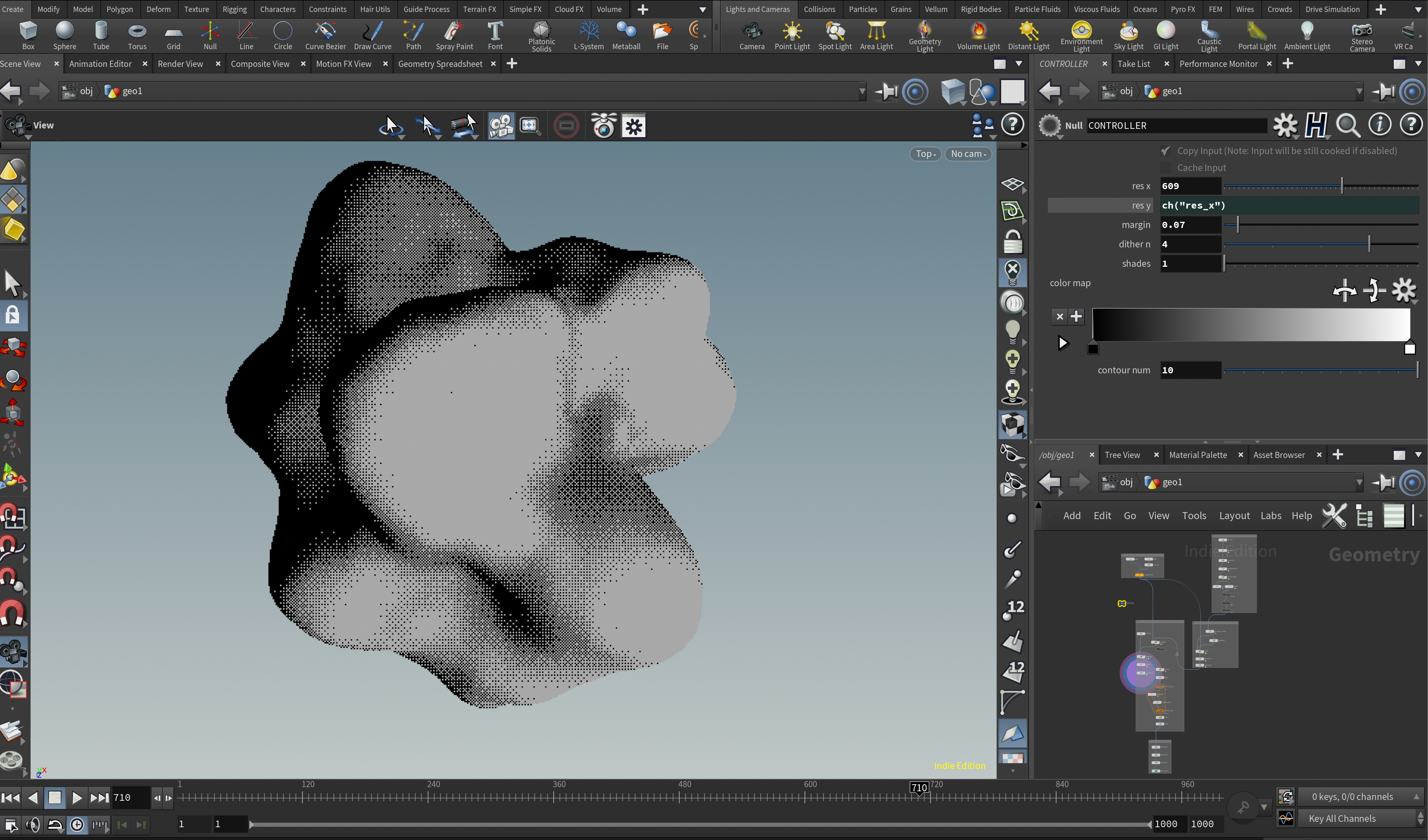
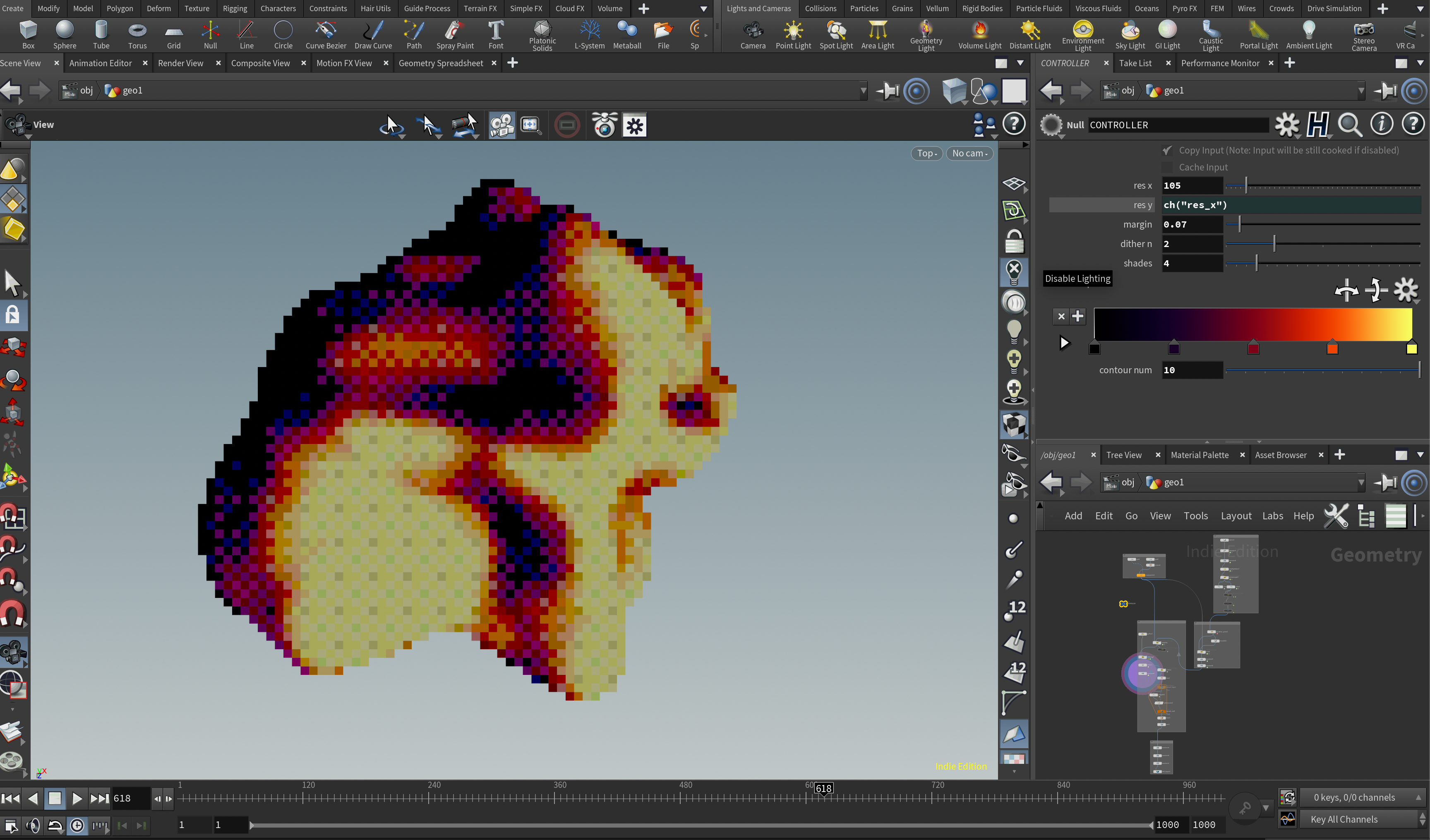
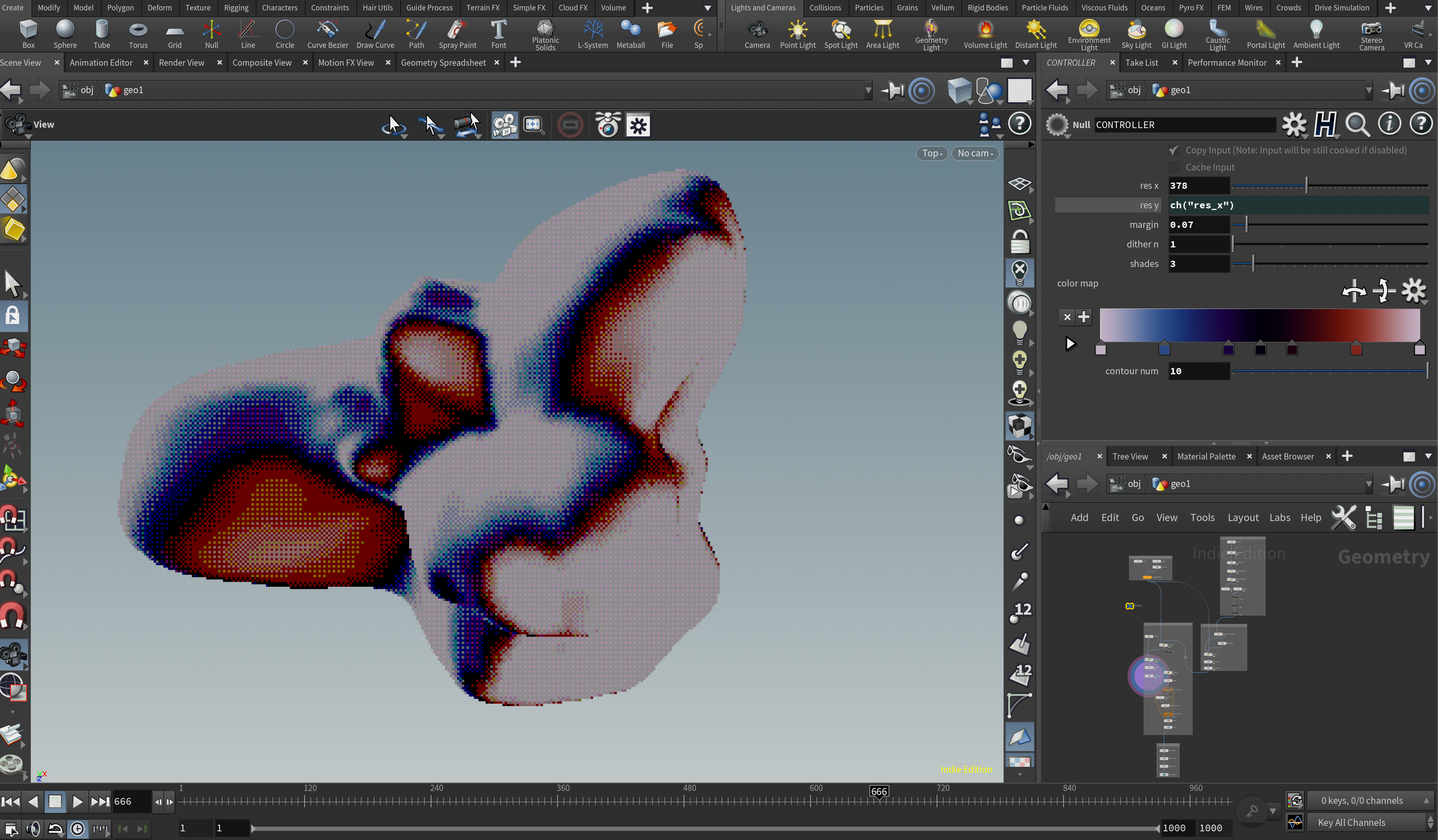
期待する結果としては以下のようなイメージです。
Ordered Ditheringは1973年にBayerによって作られたアルゴリズム("An optimum method for two-level rendition of continuous-tone pictures")で、少ない色数(例えば白と黒)の組み合わせでその間の色(グレーとか)を補間して表現するための手法です。これを使うと昔懐かしいゲームボーイやスーパーファミコンのピクセル表現を高解像度画像(あるいは形状)から自動で作ることができます。
ゴール
通常このアルゴリズムはビジュアライズの用途で使われることがほとんどなので、高速に処理できるシェーダーで実装されることが多いですが、今回はわざわざメッシュオブジェクトとしてHoudiniでVEXを使って実装してみたいと思います。
理由は三点。
- シェーダーより実行速度は遅いけど実装しやすいので、アルゴリズムの勉強にちょうどいい◎
- 別の3D形状との掛け合わせが可能○
- 同じ要領で3Dボクセルディザリングも作れるはず△(今回は作りません)
個人的にはアルゴリズムの学習目的のためにまずHoudiniのVEXで実装してみることが多いです。メッシュ構造やボクセルを手軽に比較的速い速度で扱えるというのが大きいです。あとデバッグしやすい。
ディザリングのアルゴリズムの基本
まずは、メインとなるディザリングのアルゴリズムをWikipediaの解説を元に簡易に説明します。今回使うのはBayerが提唱したアルゴリズムで、内容は簡単にいうとピクセルをNxN(例えば4x4)のピクセルのかたまりがたくさん並んでいるものと考え、それぞれのかたまりで事前に用意しておいたしきい値マップを利用して各ピクセルの色を色数を抑える形で置換していくというものです。
しきい値マップは色々な形が存在しているようですが(しきい値マップの作りかたによって出てくるディザリングの見え方が変わる)、一番一般的なのは上の図のように2のべき乗のサイズのマップ(行列)を使う場合が多いようです。上の図のような行列はBayer行列とも呼ばれるようです。
この任意のサイズの行列をピクセル画像にオーバーレイして、そのピクセルに対応した数値(しきい値)を見て、(色数が白黒の場合)そのピクセルを白にするか黒にするか選ぶという使い方になります。
計算式として表現する場合、次のような再帰的な計算式で表現することができます。
関数で表現することもでき、
Mpre(i,j) = (Mint(i,j)+1) / n^2
と書くことができます。iは行列の行の位置、jは行列の列の位置を示しています。
最終的に n^2で割ることによって、行列の中の各しきい値が0~1になるように正規化しています。正規化することで、ピクセルの色(RGBがそれぞれ0~1の範囲にある)と比較がしやすくなるという寸法です。しきい値よりもピクセルの値が小さければ0にして、大きければ1にするといったすんぽうです。
色数コントロールできるディザリングのアルゴリズム
ただ0か1にしかならないとなると、白黒、あるいはだいぶビビッドないろの表現しか作れないので、色数を増やすためにクオンタイズの概念と導入します。クオンタイズとは、ある数値を限られた数値で丸める手法です。画像処理とか音楽とかでよく聞く語だと思います。
そのクオンタイズを導入すると、先のしきい値行列から値を取得する関数は次のように表現できます。
このnearest_palette_colorという関数がクオンタイズをしている部分で、cはオリジナルの色を示しています。M(x mod n, y mod n) - 1/2は先に出てきたしきい値から指定した行列の位置にある値を取得する関数です。最後の1/2は値を-0.5から0.5の範囲に正規化するための追加ステップです(別になくても大丈夫ですが、グレースケールじゃなくて色を扱う場合はこのほうがより自然な色がでるようです)。
でも個人的には-0.5しない方がグレースケールに関しては良い気がしたので、このステップはスキップします。
では実際にこのアルゴリズムをHoudiniのVEXを実装したいと思います。
作りたい流れ
まずHoudiniでディザリングの仕組みを作るにあたって、何をインプットにして何をアウトプットとして出したいのかを整理します。
インプット
- ピクセル化したい3D形状
- 形状を見るためのカメラ
- ディザリング用の各種パラメータ(解像度、色数他)
アウトプット
- 個別の面に色がついたグリッドメッシュ
その上で次のような流れを作りたいと思います
プロセス
- ピクセル化したい3D形状を作る
- ピクセル化用のキャンバス(グリッド)を作る
- カメラを作って2D化したい画角を設定する
- 3D形状を2D化する
- 2D形状の色を解像度設定したグリッドに転写する
- ディザリングのアルゴリズムを使って色数を減らす
今回のメインはステップ5の部分なので、そこを重点的に説明したいと思います。
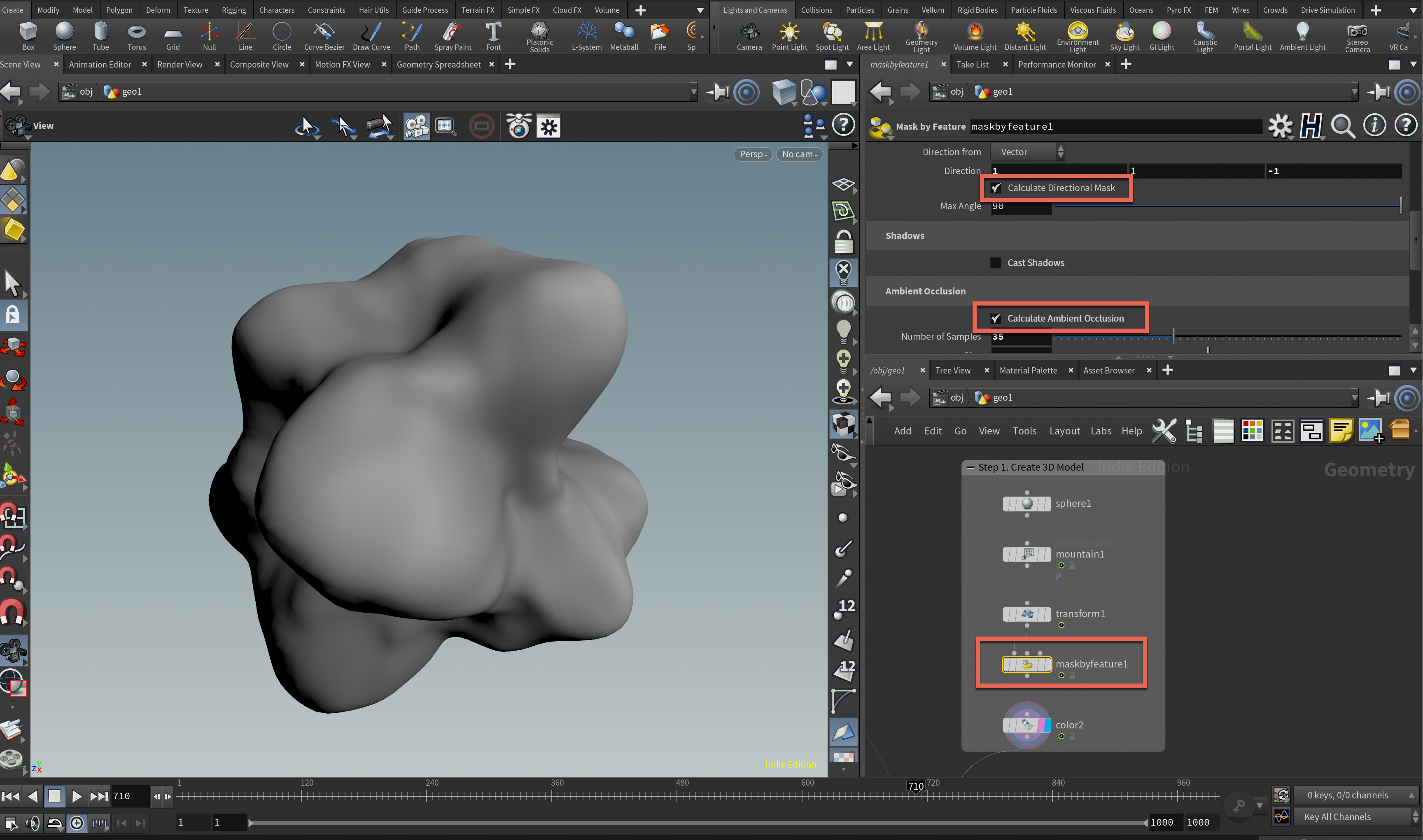
Step 1. ピクセル化したい3D形状を作る
形状はどんな形でも使えるようにしたかったので、サンプルとしては至極シンプルな形状にしています。球体をMountainノードで歪ませて、それにMaskByFeatureノードで擬似的な影を生成しています。今回はこのノードで作られた影(PointのCdというアトリビュート)をベースにピクセル化を行いたいと思います。
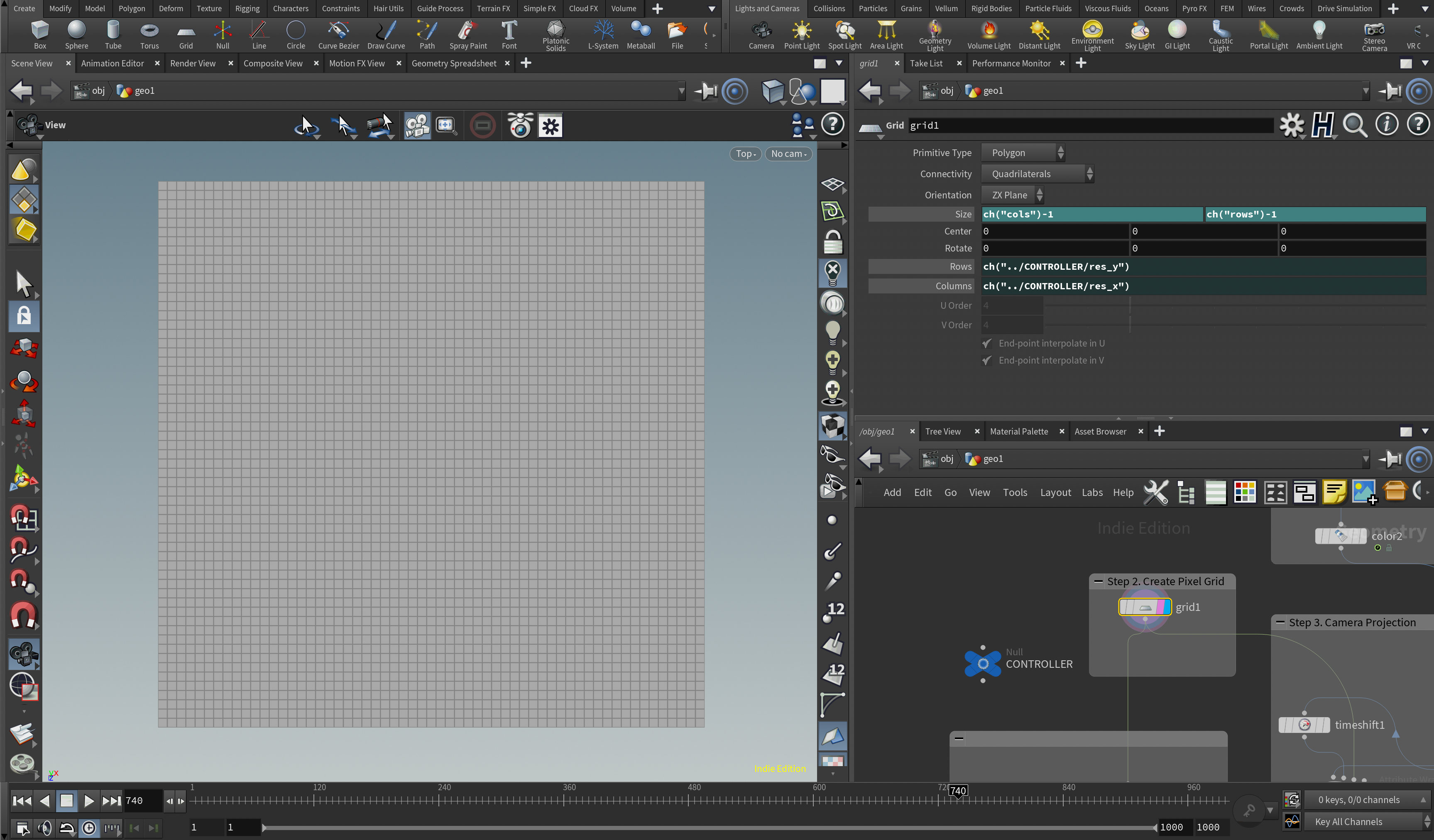
Step 2. ピクセル化用のキャンバス(グリッド)を作る
次に3D形状をピクセル化するにあたって利用するキャンバス(グリッド)を作ります。単にGridノードを使って作ります。ここで設定したグリッドの解像度がそのままピクセルの解像度になります。
Step 3. カメラを作って2D化したい画角を設定する
今回は元が3D形状なので、最終的にピクセル化するにあたって2Dに投影する必要があります。その方法として、せっかく3Dツールを使っているのでHoudiniで作ったカメラを利用してカメラ投影することにします。実装的に一番簡単なのは平行投影ですが、カメラ投影を使えば広角カメラによる見え方をそのまま2D化するみたいなこともできるので色々と表現の幅が広がります。
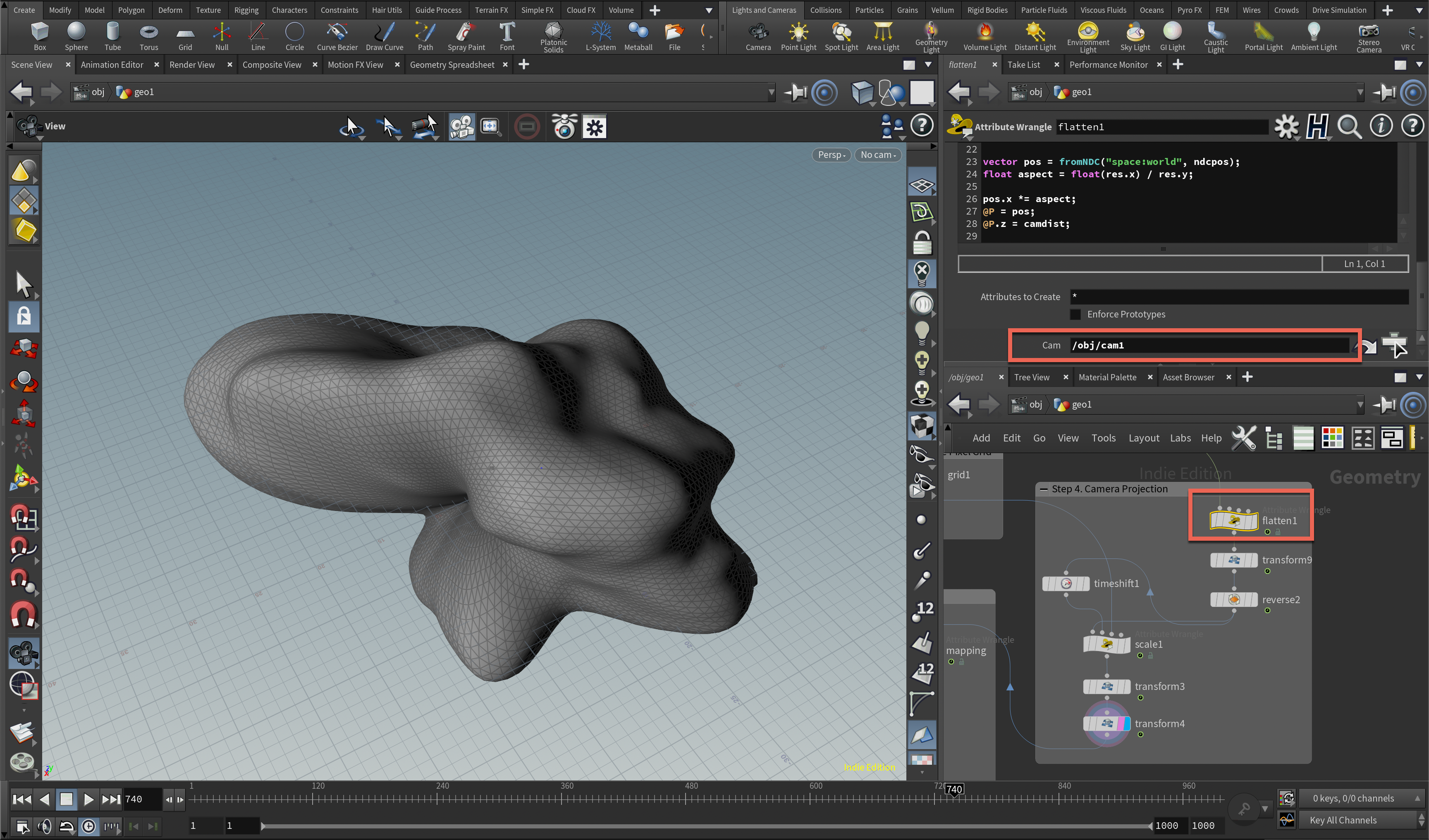
Step 4. 3D形状を2D化する
以前行ったグラフィクスの展示でもよく使いましたが、3Dを指定したカメラで2Dに投影します。よく使うカメラ投影のスニペットを貼っておきます。基本的にはPoint Wrangleを使ってD形状のポイントを指定のカメラを使ってXZ平面に投影します。カメラの指定はOperatorのパスのUIを作って行っています。
string campath = chs("cam"); // カメラへのパス
matrix camMat = optransform(campath); // カメラからカメラ行列を取り出す
vector campos = cracktransform(0, 0, 0, set(0,0,0), camMat); // カメラ行列からカメラ位置を取り出す
float camdist = distance(campos, @P); // カメラ位置とメッシュのポイントとの距離を測る
vector ndcpos = toNDC(campath, @P); // ポイント位置をカメラ座標(カメラから見てX,Y軸は0~1、Z軸はマイナスを使ってカメラの距離)に変換する
// カメラから諸々パース情報を取得する
float focal = chf(campath + "/focal");
float aperture = chf(campath + "/aperture");
vector2 res = chu(campath + "/res");
float near = chf(campath + "/near");
float far = chf(campath + "/far");
// カメラのパース情報からパースペクティブ行列を作る
matrix pers = perspective(
focal / aperture,
float(res.x) / res.y,
float(res.y) / res.x,
near,
far
);
// パースペクティブ行列の逆行列を取って、カメラ座標に適用する
pers = invert(pers);
ndcpos *= pers;
vector pos = fromNDC("space:world", ndcpos); // カメラ座標からワールド座標に変換する
// カメラ情報からアスペクト比を作って座標に適用する
float aspect = float(res.x) / res.y;
pos.x *= aspect;
@P = pos; // ポイントを投影座標に移動する
@P.z = camdist; // Z座標にメッシュのポイントとカメラ間の距離を適用する
一般的にどんな言語でも使えるような投影方法ですが、最後に行っている@P.z = camdist; の部分は、あえて奥行き情報が残るように設定している特殊な部分です。これは後で効いてきます。
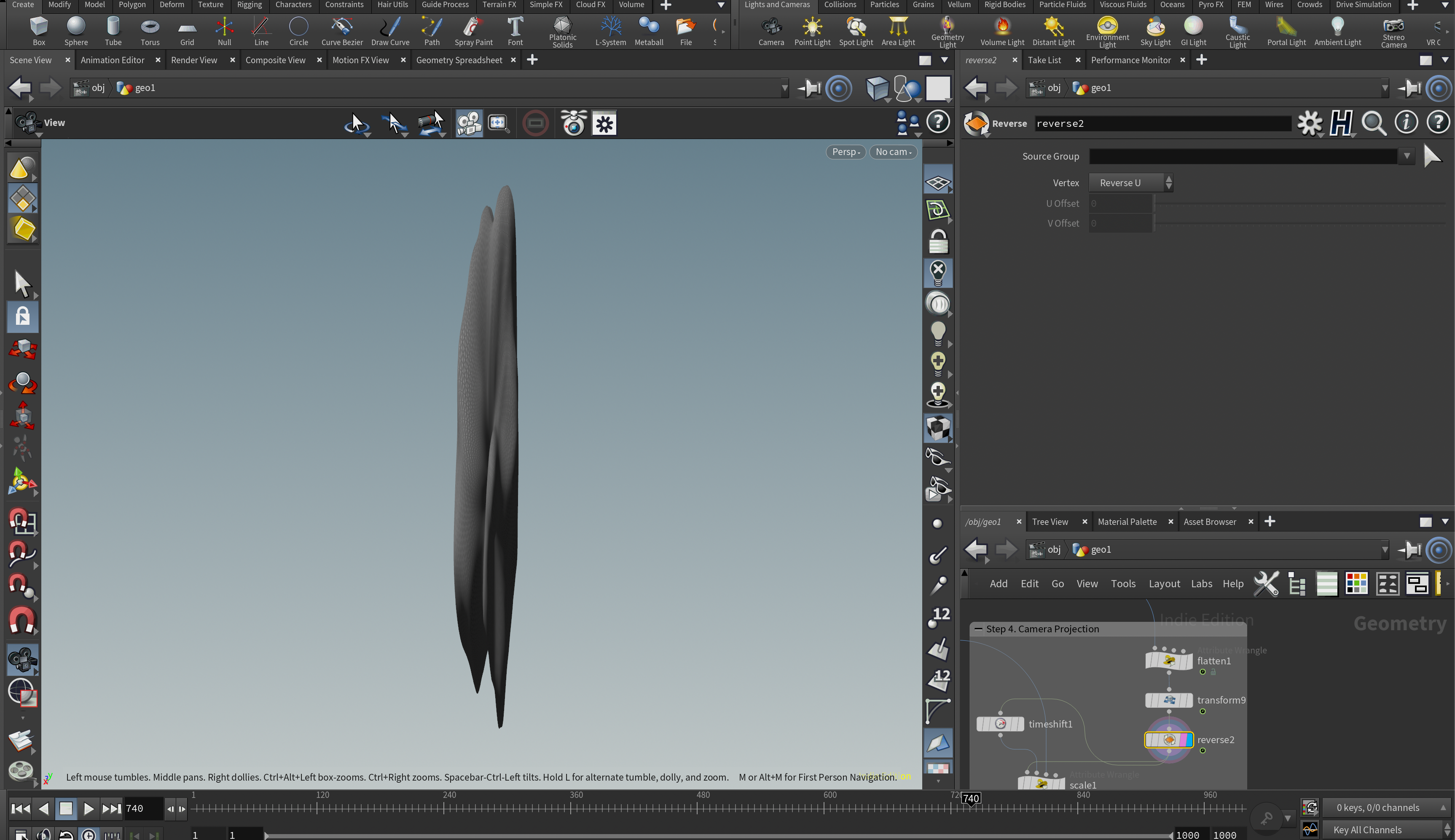
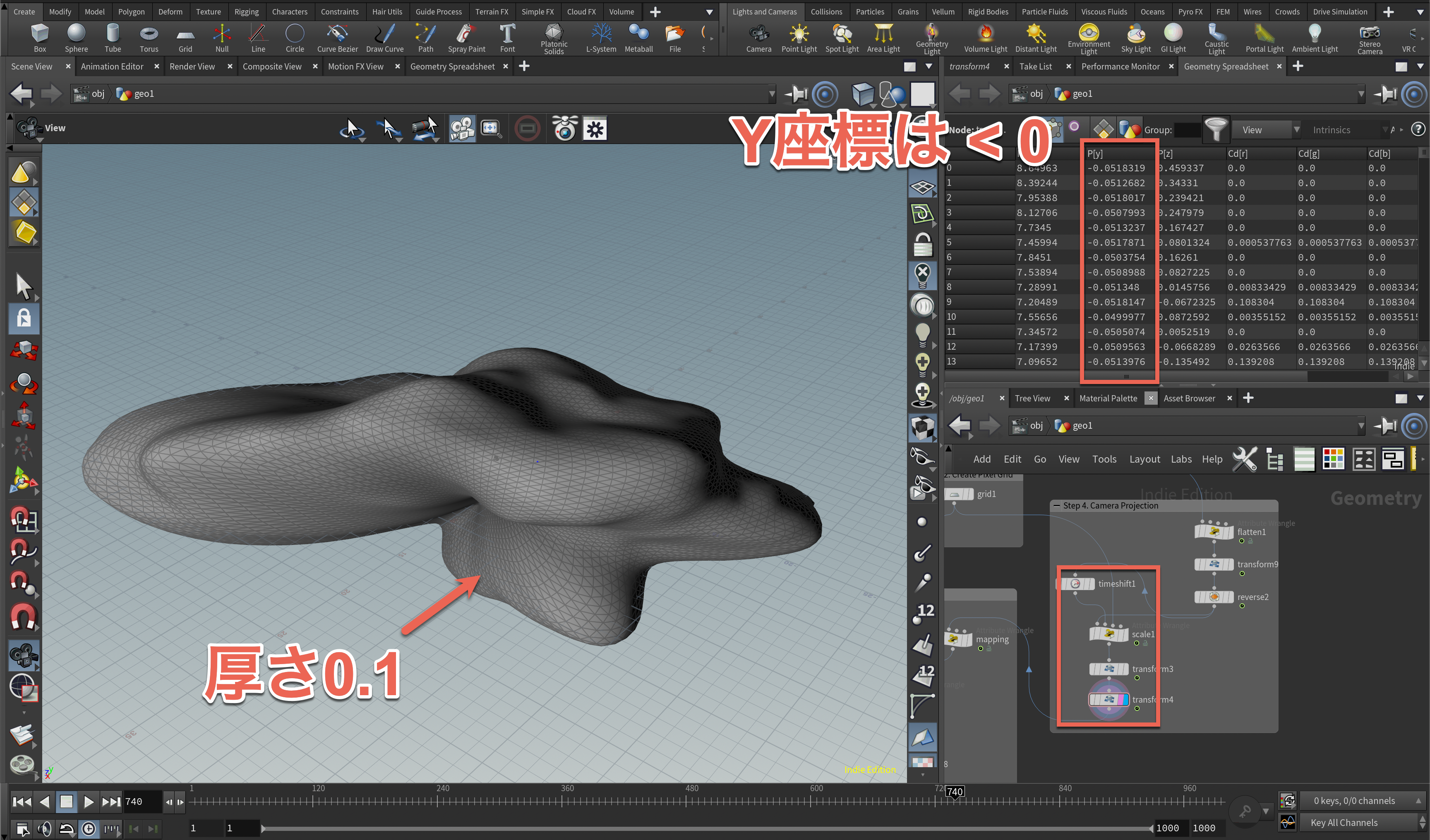
ただこのままだと高さ方向に以上に伸びたモデルになっちゃいます。
奥行き方向のサイズは本当に微妙にあればいいので(例えば全体のサイズが100に対して0.1とか)、Transformノードなどを使って奥行きが0.1になるように調整します。また回転とか移動も利用して、XZ平面状に基本微妙に奥行き情報がある2D(2.5D)形状をY座標が0よりも小さい位置に配置しておきます。
このあたりの調整が、高速に3D形状をピクセル化するにあたって結構有効に働くことになります。
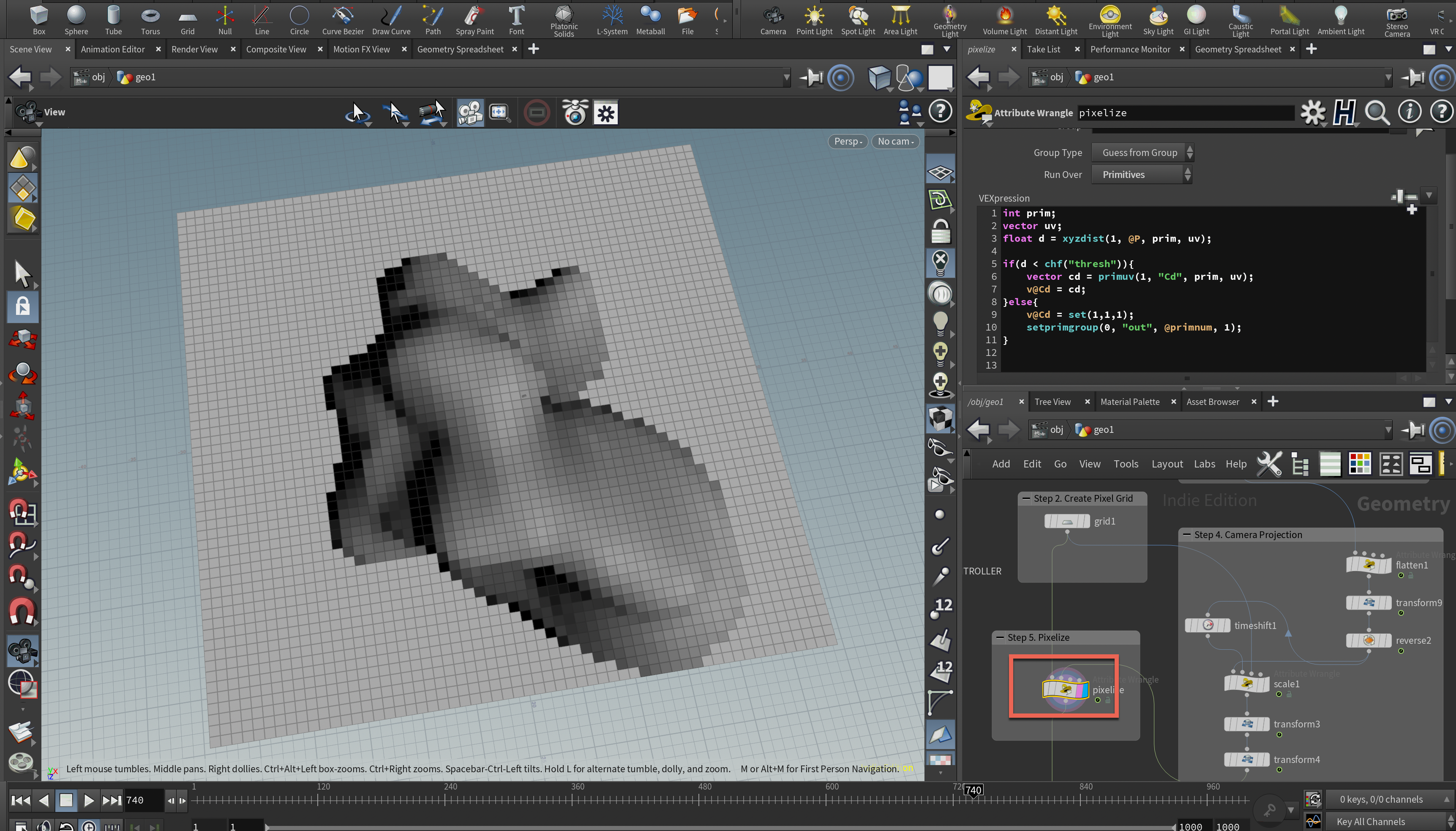
Step 5. 2D形状の色を解像度設定したグリッドに転写する
ステップ2で作ったグリッドに、ステップ4で作った2次元メッシュ(厳密にいうと0.1分微妙に奥行きがあるので2.5Dかな?)をPrimitive Wrnagleを使って色を転写します。その時のコードが次のような形になっています。
// xyzdist関数を使って各グリッドセルから一番近い
// 2Dメッシュのプリミティブ情報を取得する
int prim;
vector uv;
float d = xyzdist(1, @P, prim, uv);
// グリッドと2Dメッシュの距離が0.1以下の場合、
// 2Dメッシュはそのグリッドに限りなく近いという前提のもと、
// その条件を満たす場合は2Dメッシュから色を転写する。
// それ以外は、外側にあるというグループに入れる。
if(d < chf("thresh")){
vector cd = primuv(1, "Cd", prim, uv);
v@Cd = cd;
}else{
v@Cd = set(1,1,1);
setprimgroup(0, "out", @primnum, 1);
}
よく思いつくやり方としてはxyzdist関数よりもintersect関数を使う方法があるかと思います。そのほうが自由度が高いですし、いちいち0.1以下の範囲にあるかなんて条件を書く必要がありません。ただ、計算速度はxyzdistのほうが圧倒的に速く、ただ素早く計算したいがためにintersectの代わりにxyzdistを使っています。塵も積もれば山になると言いますし、なるべく計算コストの高くない方法で機能を作っていきたいという気持ちが自分には強いす(素早くたくさんバリエーション試したいですし)。
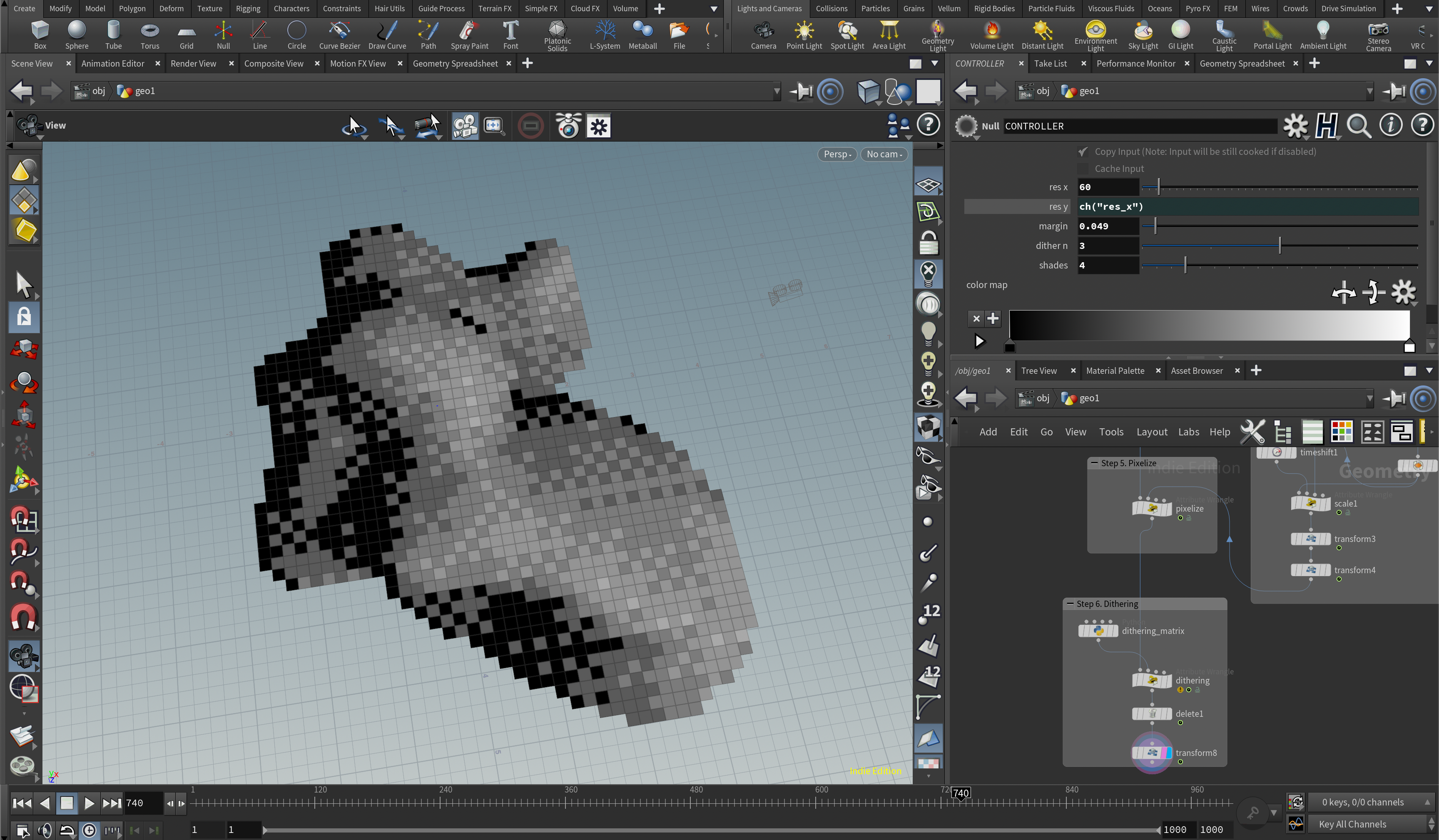
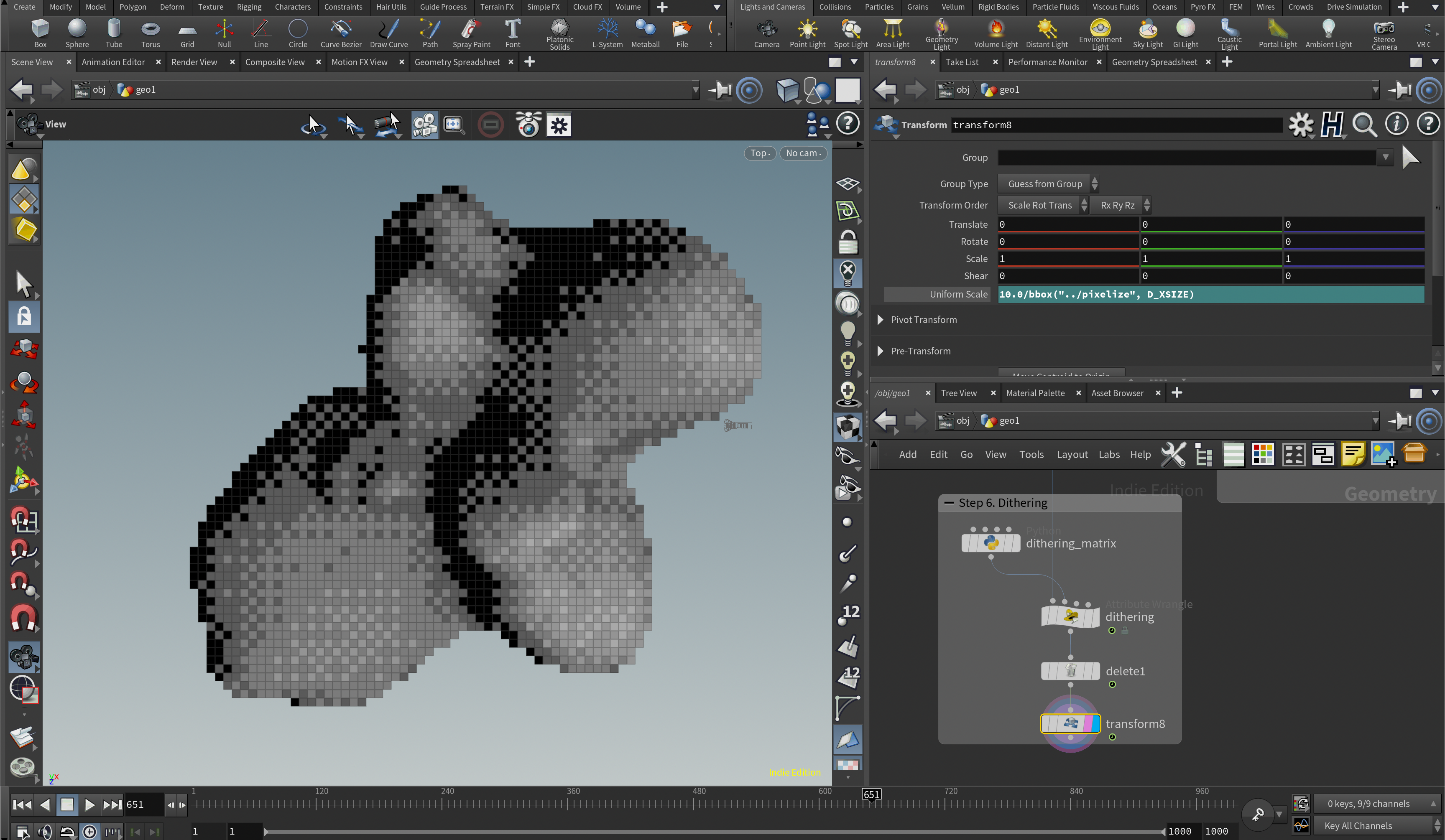
Step 6. ディザリングのアルゴリズムを使って色数を減らす
6-1. PythonでBayer行列を配列として作る
3D形状をピクセル化すること自体はステップ5まででできますが、そこから色数を制限することでより8bit風、16bit風な表現に近づけることができます。そこで出てくるのがディザリングです。
先に説明したアルゴリズムを実装していきたいのですが、一点VEXだけでは実現できない部分があります。それが再帰的にしきい値マップを作る次の関数です。
Mpre(i,j) = (Mint(i,j)+1) / n^2
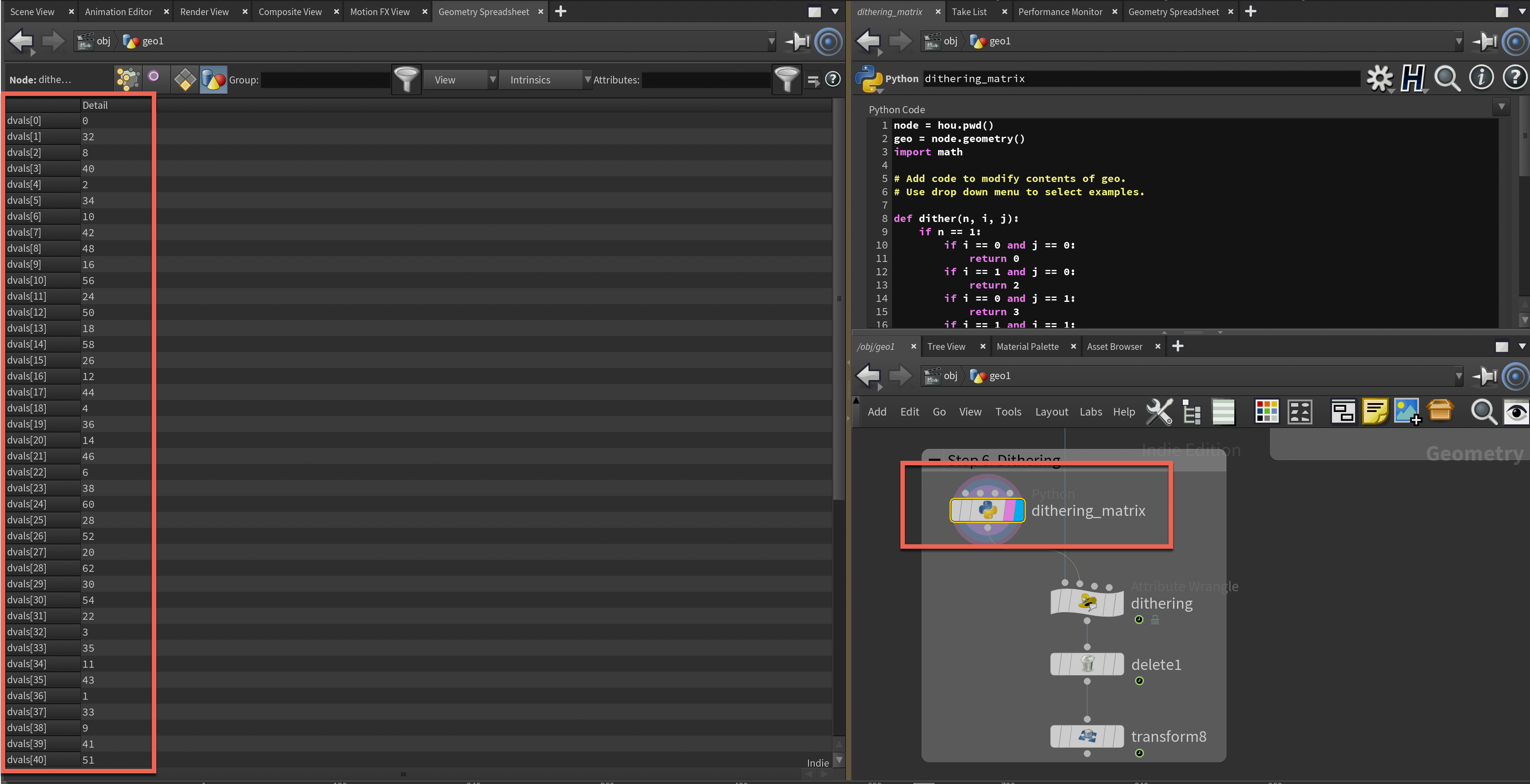
ということで、再帰的にしきい値マップを作るところだけはPythonを利用することにします。
ただDitheringの計算自体はVEXで並列計算させたいので、行列の情報を配列としてDetailのアトリビュートに持たせることにしました。しきい値行列のNだけ決めて、そのNに応じてしきい値行列を配列に変換したものを作ります。N=8の場合は、8x8=36個のしきい値が入った配列が入っているということです。コードは次のように書いています。
node = hou.pwd()
geo = node.geometry()
import math
# サイズnのしきい値行列のi行, j列の位置にある
# しきい値を取得する再帰関数
def dither(n, i, j):
if n == 1:
if i == 0 and j == 0:
return 0
if i == 1 and j == 0:
return 2
if i == 0 and j == 1:
return 3
if i == 1 and j == 1:
return 1
elif n > 1:
v1 = dither(n-1, math.floor(i * 0.5), math.floor(j * 0.5))
v2 = dither(n-1, i % 2, j % 2) * 4
return v1 + v2
n = node.parm("n").eval();
dvals = []
num = pow(pow(2, n), 2)
# n x n行列の各しきい値を配列に入れる
for s in range(num):
i = s % pow(2.0, n)
j = math.floor(s / pow(2.0, n))
dval = dither(n, i, j)
dvals.append(dval)
# Detailのアトリビュートにしきい値配列を入れる
geo.addAttrib(hou.attribType.Global, "dvals", dvals)
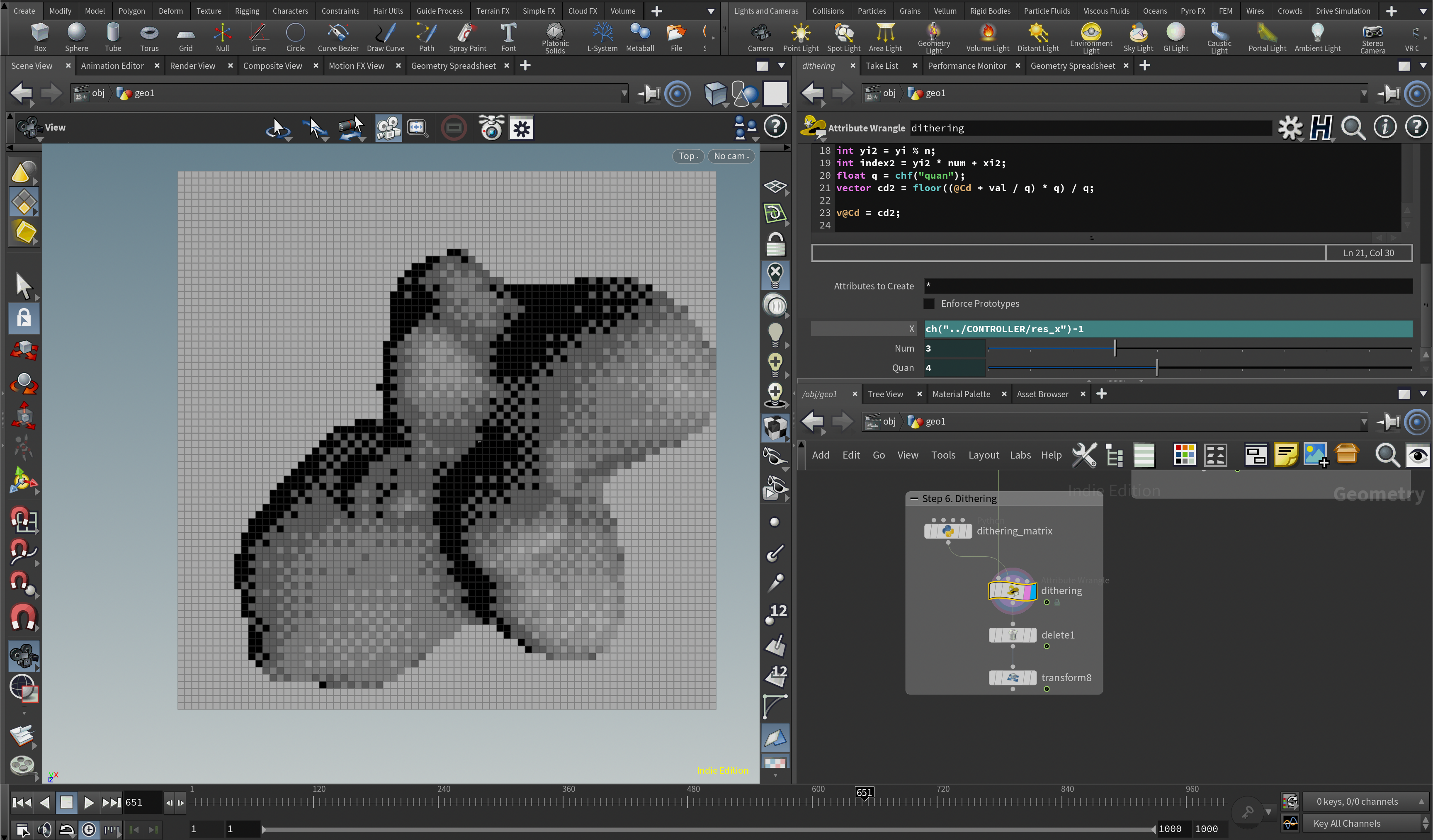
6-2. しきい値行列を使って色を置換する(ディザリング)
いよいよディザリングを行います。Primitive Wrangleを使い、6-1で作ったしきい値配列を参照して色のクオンタイズも加えて色を置換していきます。そのとき、インプットとして任意にコントロールできる色数のパラメータを使います。
float dvals[] = detail(1, "dvals"); // Detailのアトリビュートからしきい値配列を取得する
int n = chi("num"); // しきい値行列の大きさ
int num = pow(2, n); // 2のn乗の値を計算
int xnum = chi("x"); // ピクセル表現するグリッドのX方向のセルの数
// 各ピクセルのX方向とY方向の番号を取得する
int xi = @primnum % xnum;
int yi = floor(@primnum / float(xnum));
xi = xi % num;
yi = yi % num;
int index = yi * num + xi; // しきい値配列に対応したインデックスを作る
float val = dvals[index] / pow(num, 2.0); // 正規化されたしきい値を計算する
float q = chf("quan"); // 色数
vector cd2 = floor((@Cd + val / q) * q) / q; // しきい値を利用して色をクオンタイズする
v@Cd = cd2; // 色を設定
6-3. 3Dメッシュの外のピクセルを消す
最後の処理として、3D形状の外にあるピクセルを削除します。この処理は特に重要ではないですが、メッシュとしてグリッドを扱っているならではの表現にはなっているかと思います。
プロジェクトファイル
今回作ったファイルは以下のURLからアクセスすることができます。
おわりに
いかがでしたでしょうか。Ordered Ditheringのアルゴリズム自体は簡単なものですが、個人的に色を加えたときにどうやるのだろうというイメージがなかなかつかず、Wikipediaの色付きのDitheringの項をずっと読んで、答えとして出したのが以上の方法です。もしかしたら厳密には異なることをしているかもしれませんが、結果として得られた絵はそれなりに満足いくものになったので良しとします。
それではHappy Holiday!