この記事はHoudini Apprentice Advent Calendar 2024の13日目の記事です。
内容は、Pointを並び替えるための様々なTipsについてです。Houdini上でPointの順番を自由にコントロールする方法を紹介します。最近、この並び替えを頻繁に行う機会があり、その中で得た知見を共有したいと思います。
並び替えをカスタムにコントロールする理由のひとつに、少しニッチな話になりますが、Pointを任意の順番で呼び出すことで、Digital Fabrication用のG-Codeデータなどを作成する際に出力順を調整できるという点があります。
Digital Fabricationとは、デジタルデータを使って物理的な加工(切削、3Dプリント、プロッティングなど)を行う技術の総称です。例えば、FDMタイプの3Dプリンターでは、ノズルの動きやフィラメントの吐出量をG-Codeでコントロールすることが可能です。
過去に、デザイナーの深地さんと「Digraph」というユニットでNATURE/CODE/DRAWINGという展示を行いました。この展示ではプロッターを使ったペンドローイングを披露しましたが、プロッターとは、3Dプリンターのようにペンを指定したパスに沿って動かし、ドローイングを行う機械です。このとき、PointやPrimitiveの順番をコントロールすることで、線の描き順を細かく調整することが非常に重要でした。物理的なメディアを使っているので、描けば描くほど摩擦でペン先が摩耗し、最初濃かった線も最後には薄くなっていくといったことがあるため、どの順番で描くのかということが非常に重要でした。
また、今年9月に京都工芸繊維大学で行った3Dクレイプリンターのワークショップでは、Houdiniから直接G-Codeを出力し、3Dプリンターを制御する試みも行いました。この場合も、ノズルの動きはPointの順番に依存するため、順番を正しく揃えることが非常に重要でした。
以上のような背景を踏まえ、この記事ではHoudiniでPointを様々な方法で並び替えるテクニックを紹介していきます。基本的にはPoint Wrangleノードと、Sortノードの組み合わせで行います。
0. テストデータ
基本的な流れとしては、PointやPrimitiveの順番に応じた数値のアトリビュートを作り、それに応じてSortノードでソートするだけです。
先にソートを試すためのテストデータをいくつか用意しておきましょう。
0-1. XZ平面上にランダムに配置されたポイント
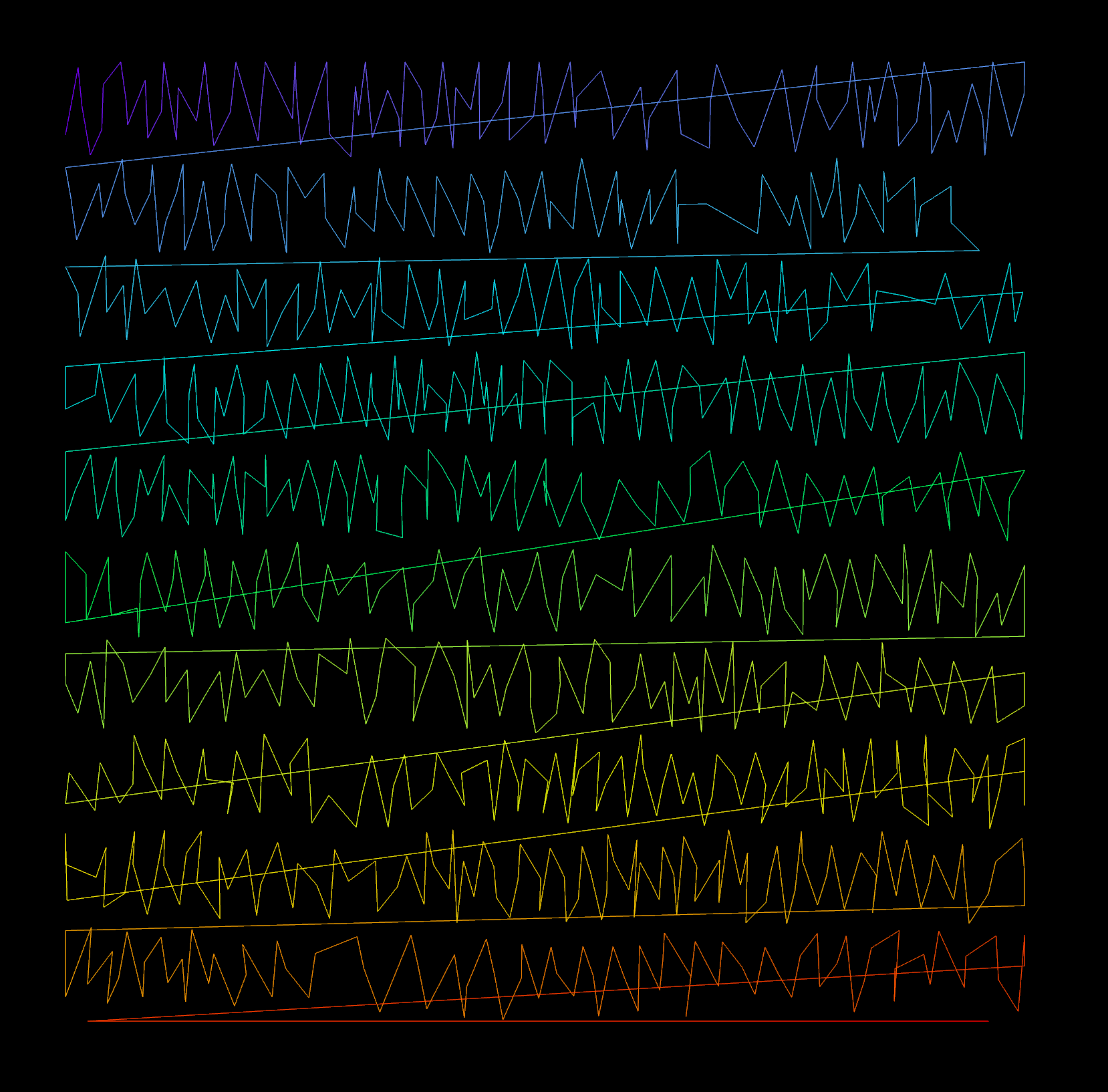
Grid平面上にランダム散布した点群を作ります。ポイントの色のグラデーションは順番を示しています。
0-2. 高さ方向に積んだ歪んだ環状曲線
円形ポリラインを高さ方向に積み上げてノイズ関数で歪ませます。各円形の頂点の順番をSortノードでランダムに並び替えています。ポイントの色のグラデーションは順番を示しています。
1. 平面上の点群の並び替え
平面上にランダム散布された点群を様々な形で並び替えてみましょう。並び替えたポイントは、どのような順番になっているかわかりやすいように、最終的にAddノードを使ってポリライン化して可視化してみます。
1-1. 複数行に分解して行ごとに水平に並び替える
まずは、平面上の点群を垂直方向(Z方向)に任意の分割数で分割して、各行にある点群を水平方向(X方向)に並び替えます。その際、一行目の水平並び替えが終わったら、次の行にいってまた水平に並び替えるということをやりたいと思います。ペンプロッターでなるべくパスの全体のパスの長さを短くする上で有効な並び替えです。
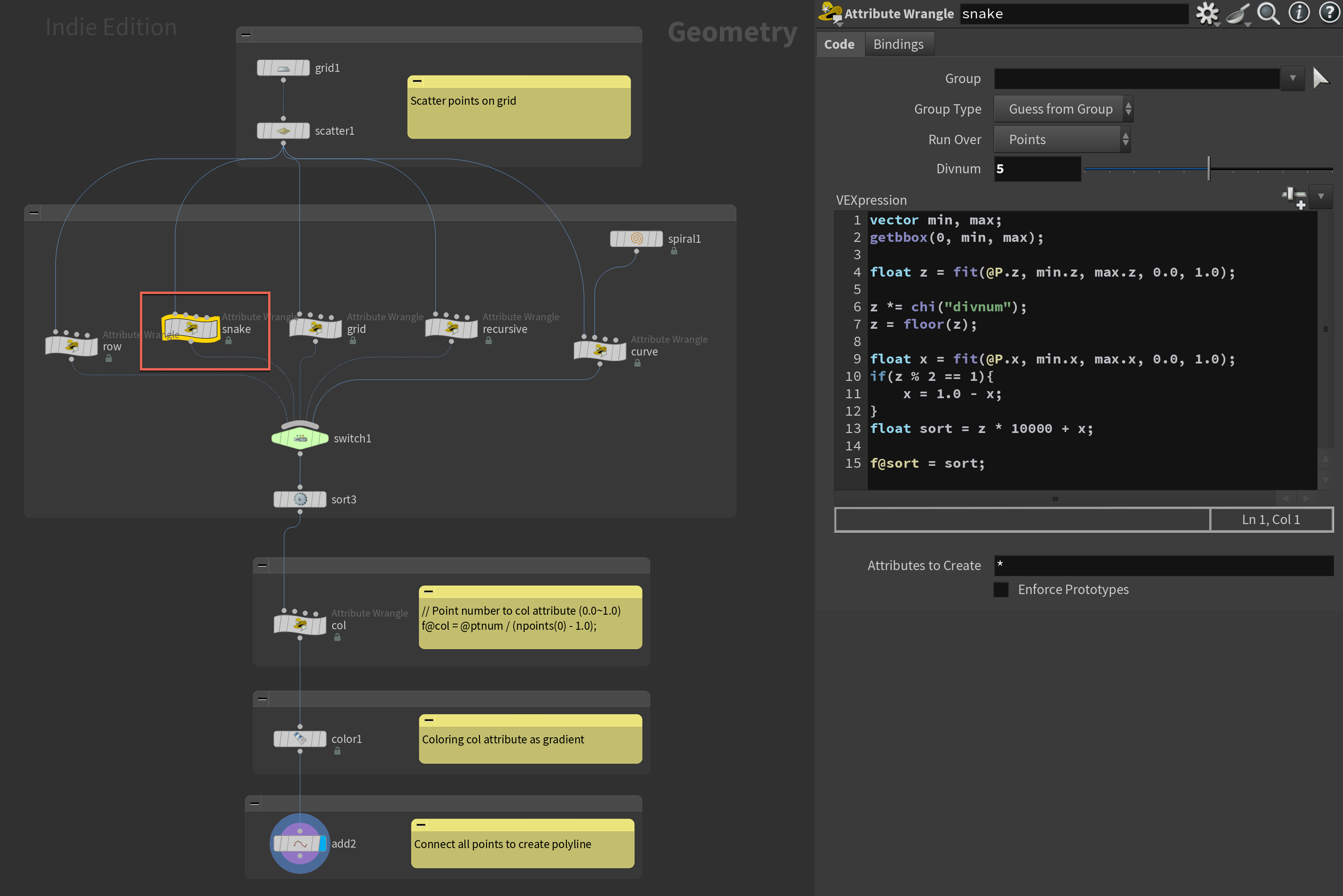
Point Wrangleで下記のコードを記述し、SortノードでPointをsortアトリビュートに沿って並び替えるように設定します。
vector min, max;
// バウンディングボックスの最小・最大座標を取得
getbbox(0, min, max);
float z = fit(@P.z, min.z, max.z, 0.0, 1.0);
z = floor(z * chi("divnum"));
// Z座標を正規化し、分割数でスケールして丸める
float x = fit(@P.x, min.x, max.x, 0.0, 1.0);
// X座標を正規化
float sort = z * 10000 + x;
// Z座標を重み付けしX座標と組み合わせて並び順を生成
f@sort = sort;
// 並び順をポイントアトリビュートに保存
ここで覚えておきたいテクニックは、Z座標とX座標をそれぞれ重み付けを変えて組み合わせ、並び順を生成している下記コードの部分です。まず行順を優先させたいので、列の番号を示すzの値に大きめな数値を掛け、その上で、各行で水平に並び変えるためにX方向の座標情報を示すxを足しています。
float sort = z * 10000 + x;
// Z座標を重み付けしX座標と組み合わせて並び順を生成
1-2. 複数行に分解して行ごとにピンポン状に並び替える
1つ目に行った並び替えと同じように垂直方向に点群を分割して、水平方向に並び替えますが、行の番号が奇数か偶数かに応じて、水平方向の並び替えの方向を変えます。例えば奇数方向だったら右方向に並び替え、偶数行だったら左方向に並び替えということをしたいです。こうすることで、よりすべての点を通るパスがより短くなり効率的になることを狙っています。
Point Wrangle内には次のように書きます。
vector min, max;
// バウンディングボックスの最小・最大座標を取得
getbbox(0, min, max);
float z = fit(@P.z, min.z, max.z, 0.0, 1.0);
z = floor(z * chi("divnum"));
// Z座標を正規化し、分割数でスケールして丸める
float x = fit(@P.x, min.x, max.x, 0.0, 1.0);
if (z % 2 == 1) {
x = 1.0 - x;
}
// 奇数行のZ座標の場合、X座標を反転
float sort = z * 10000 + x;
// Z座標を重み付けし、反転後のX座標と組み合わせて並び順を生成
f@sort = sort;
// 並び順をポイントアトリビュートに保存
先に行った並び替えとほぼ同じ書き方ですが、下記の部分で行の数を示すzの値が偶数か奇数かに応じて、xの値を反転させています。
float x = fit(@P.x, min.x, max.x, 0.0, 1.0);
if (z % 2 == 1) {
x = 1.0 - x;
}
// 奇数行のZ座標の場合、X座標を反転
1-3. グリッド上に分解してピンポン状に並び替える
今度は垂直方向に加えて水平方向にも分解して、グリッド上に点群を分解し、グリッドのセル毎に点を並び替えて行くこともやってみましょう。パーツパーツでパスを固まって書いていくような形になります。
Point Wrangleには次のように書きます。
vector min, max;
// バウンディングボックスの最小・最大座標を取得
getbbox(0, min, max);
float z = fit(@P.z, min.z, max.z, 0.0, 1.0);
z = floor(z * chi("znum"));
// Z座標を正規化し、分割数でスケールして丸める
float x = fit(@P.x, min.x, max.x, 0.0, 1.0);
x = floor(x * chi("xnum"));
// X座標を正規化し、分割数でスケールして丸める
vector cen = set(fit01(x / chi("xnum"), min.x, max.x),
0.0,
fit01(z / chi("znum"), min.z, max.z));
// 現在のセルの中心座標を計算
if (z % 2 == 1) {
cen = set(fit01((x + 1) / chi("xnum"), min.x, max.x),
0.0,
fit01((z + 1) / chi("znum"), min.z, max.z));
// 奇数行の場合、セル中心座標を次のセルにシフト
x = 1.0 - x;
// X座標を反転
}
float dist = distance(cen, @P);
// セルの中心と現在位置との距離を計算
float sort = z * 10000 + x * 100 + dist;
// Z, X座標と距離を組み合わせて並び順を生成
f@sort = sort;
// 並び順をポイントアトリビュートに保存
ここではまず、xを水平方向の番号として作っています。
float x = fit(@P.x, min.x, max.x, 0.0, 1.0);
x = floor(x * chi("xnum"));
// X座標を正規化し、分割数でスケールして丸める
その上で、グリッドの各セルのコーナーの点の位置cenを計算します。その際、列の番号に応じてコーナーの位置を変えています。
vector cen = set(fit01(x / chi("xnum"), min.x, max.x),
0.0,
fit01(z / chi("znum"), min.z, max.z));
// 現在のセルの中心座標を計算
if (z % 2 == 1) {
cen = set(fit01((x + 1) / chi("xnum"), min.x, max.x),
0.0,
fit01((z + 1) / chi("znum"), min.z, max.z));
// 奇数行の場合、セル中心座標を次のセルにシフト
x = 1.0 - x;
// X座標を反転
}
最終的にこのコーナーの位置から、グリッドのセルの中に含まれている点との距離distを測り、それをソートのための値として利用します。
float dist = distance(cen, @P);
// セルの中心と現在位置との距離を計算
float sort = z * 10000 + x * 100 + dist;
// Z, X座標と距離を組み合わせて並び順を生成
f@sort = sort;
// 並び順をポイントアトリビュートに保存
1-4. 再帰的に近い点順に並び替える
次にちょっと趣向を変えて、最初に一点をランダムに選択して、その点から一番近い点を次の点に、そしてまたその点に近いものを次の点に、ということを再帰的に繰り返して、点を順番に並び替える方法を試してみます。ときどき遠い点にジャンプすることもありますが、こうすることで面を充填するようなきれいめなパスが作れます。
Point Wrangleには次のようにコードを記述します。
int pt = floor(rand(chi("seed")) * npoints(0));
vector pos = point(0, "P", pt);
int pts[] = array();
// 選択済みポイントを格納する配列を初期化
for (int i = 0; i < npoints(0); i++) {
int npts[] = nearpoints(0, pos, 1000.0);
// 現在の位置に近いポイントを取得(距離1000.0以内)
int npt = -1;
for (int n = 0; n < len(npts); n++) {
npt = npts[n];
if (find(pts, npt) < 0) {
// 未選択のポイントが見つかれば選択
break;
}
}
pos = point(0, "P", npt);
// 次のポイントの位置を取得
append(pts, npt);
// 選択済みポイントリストに追加
setpointgroup(0, "chosen", npt, 1);
// 選択したポイントをグループ "chosen" に追加
setpointattrib(0, "sort", npt, i);
// 選択順序を "sort" 属性に設定
}
このコードではランダムに選んだ開始ポイントからスタートし、そこから近接する未選択のポイントを順に選択していく処理を行っています。各ステップでは、現在のポイントに近いポイントを探していて、その中からまだ選ばれていないポイントを探して選択しています。選ばれたポイントはchosenというポイントグループに追加され、選択された順序が sort アトリビュートを設定しています。この処理をすべてのポイントが選ばれるまで繰り返すことで、ランダム性を保ちながら近接性を考慮した並び替えのためのアトリビュートを作っています。
1-5. 曲線に沿って並び替える
ここでは曲線に沿ってポイントを並び替えるということもやってみます。この例ではスパイラル曲線をSpiralノードで作り、その曲線の始点から終点にかけて近くのポイントが並び替えられるようにしています。
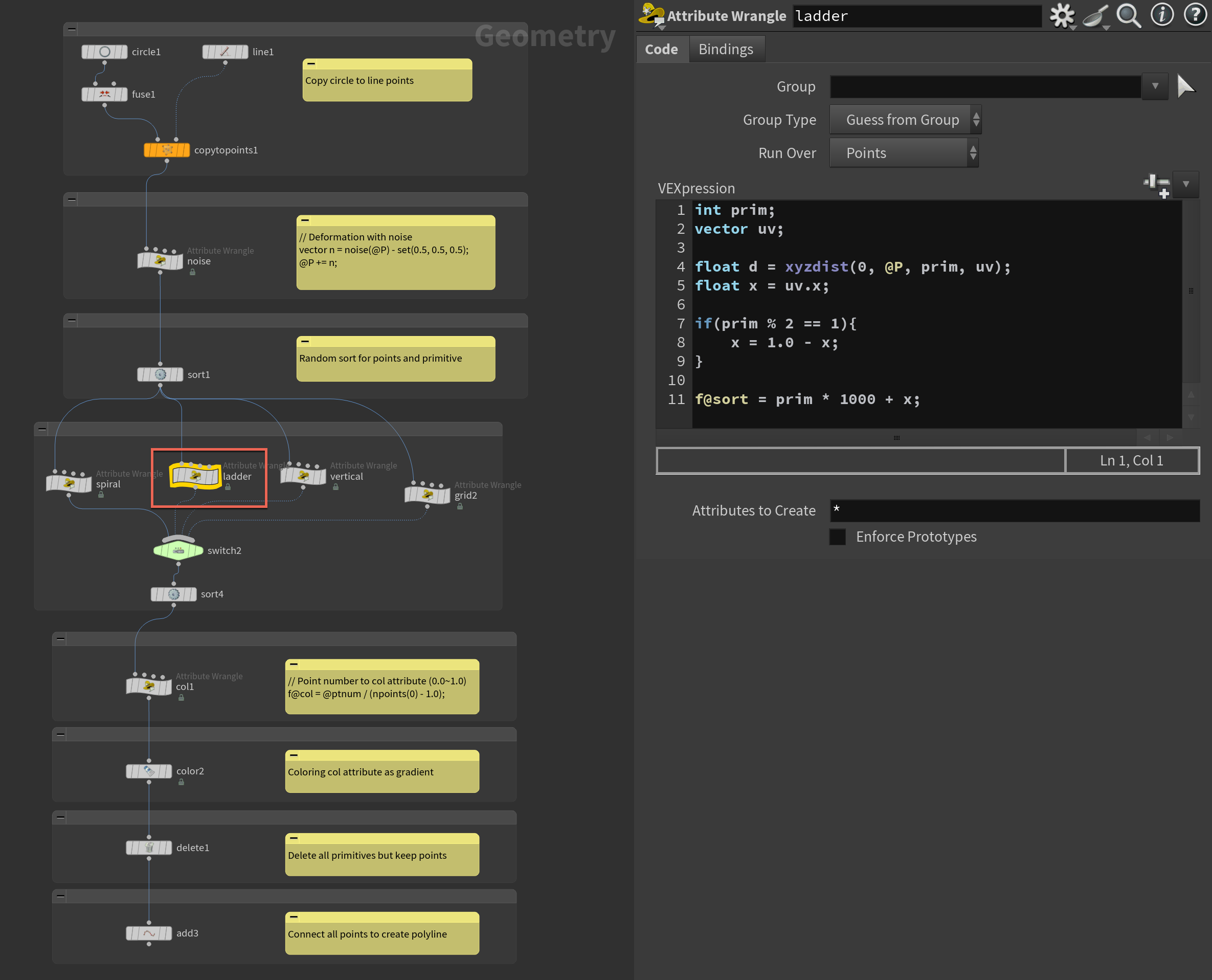
Point Wrangleには次のように書きます。
int prim;
vector uv;
float d = xyzdist(1, @P, prim, uv);
// 入力ジオメトリ1上で、現在のポイントに最も近いプリミティブとそのUV座標を取得
f@sort = uv.x;
// UV座標のU値(x成分)を "sort" 属性に保存
やっていることは単純で、各ポイントに対して、曲線との距離をxyzdist()関数で測り、それから得られるPrimitive番号とUVの値を取得し、そのUVの値をソートのためのアトリビュートとして格納しています。
2. 曲線上の点の並び替え
今度は、曲線上の点の並び替えを行ってみましょう。テストデータとしてここで用意しているのは円を高さ方向に積み上げ、ノイズ関数で全体の形状を歪ませたものです。この際、Primitive(円を歪ませた曲線)は下から上にかけて順番に並んでいる状態から行っています。また、初期状態ではPointの順番はランダムな状態にしています。
2-1. スパイラル状に並び替える
まずはシンプルに、上から下にかけてポイントがスパイラル状にのぼっていくように並び替えてみましょう。そのためには各点に対応した曲線の番号とその曲線上のUVの情報を利用します。
Point Wrangleには次のようにコードを書きます。
int prim;
vector uv;
float d = xyzdist(0, @P, prim, uv);
// 入力ジオメトリ0上で、現在のポイントに最も近いプリミティブとそのUV座標を取得
f@sort = prim * 1000 + uv.x;
// プリミティブ番号に重み付けを行い、UV座標のU値を加算して並び順を生成
各ポイントに対して、xyzdist()関数を使ってPrimitive(曲線)の番号と、その曲線のUVの値を取得し、それをそのまま並び替えのためのsortのアトリビュートとして格納します。
2-2. 各曲線毎に水平方向にピンポン状に並び替える
今度は、各曲線の番号に応じて、並び替えの方向を入れ替えることでピンポン状にパスが作られるようにしてみましょう。
Point Wrangleに次のように記述します。
int prim;
vector uv;
float d = xyzdist(0, @P, prim, uv);
float x = uv.x;
// 入力ジオメトリ0上で、最も近いプリミティブとそのUV座標を取得し、U値を取得
if (prim % 2 == 1) {
x = 1.0 - x;
}
// プリミティブ番号が奇数の場合、U値を反転
f@sort = prim * 1000 + x;
// プリミティブ番号に重み付けし、U値を加算して並び順を生成
前の並び替えとやっていることはほぼ同じで、下記のようにprimitiveの番号が奇数か偶数かに応じてUVのxの値を反転させることでピンポン状の並び替えのための数値を作っています。
if (prim % 2 == 1) {
x = 1.0 - x;
}
// プリミティブ番号が奇数の場合、U値を反転
2-3. 曲線の垂直方向にピンポン状に並び替える
今度は曲線の方向に沿わずに、垂直方向かつピンポン状にポイントを並び替えてみましょう。ここでもPrimitiveの番号とUVをうまく利用することでそれが可能となります。
int prim;
vector uv;
float d = xyzdist(0, @P, prim, uv);
// 入力ジオメトリ0上で、最も近いプリミティブとそのUV座標を取得
int pts[] = primpoints(0, prim);
// 該当プリミティブに属するポイントのリストを取得
int ind = rint((len(pts) - 1) * (uv.x % 1.0));
i@ind = ind;
// UV座標に基づいて、プリミティブ内の対応するポイントのインデックスを計算
float y = float(prim) / (nprimitives(0) - 1.0);
// プリミティブ番号を全プリミティブ数で正規化してY値を計算
if (ind % 2 == 0) {
y = 1.0 - y;
}
// インデックスが偶数の場合、Y値を反転
f@sort = ind * 1000 + y * 10;
// インデックスに重み付けし、反転後のY値を加算して並び順を生成
前の例では水平方向に並び替え、かつ曲線ごとにピンポン状に並び替えの方向を変えていたので、その時に利用してた曲線の番号の代わりに、ここでは水平方向の番号を取得し、かつ縦方向の値を0~1の範囲の値として作ります。そうすることで前のコードを流用することで垂直方向のピンポン状の並び替えが行えます。
水平方向のポイントの番号は次のようにUVから計算しています。
int pts[] = primpoints(0, prim);
// 該当プリミティブに属するポイントのリストを取得
int ind = rint((len(pts) - 1) * (uv.x % 1.0));
i@ind = ind;
// UV座標に基づいて、プリミティブ内の対応するポイントのインデックスを計算
そして垂直方向の値は次のように算出し、それを利用してsortの値を作ります。
float y = float(prim) / (nprimitives(0) - 1.0);
// プリミティブ番号を全プリミティブ数で正規化してY値を計算
2-4. 2層毎にギザギザに並び替える
最後に、各二曲線毎に、ギザギザにポイントをむすんでいくような並び替えを行ってみましょう。基本的な考え方はこれまでと同じで、曲線の番号とUVの組み合わせで実現可能です。
Point Wrangleには次のように記述します。
int prim;
vector uv;
float d = xyzdist(0, @P, prim, uv);
// 入力ジオメトリ0上で、最も近いプリミティブとそのUV座標を取得
float x = uv.x;
int y = floor(prim / 2.0);
// プリミティブ番号を2で割った商をY値とする
int pts[] = primpoints(0, prim);
// 該当プリミティブに属するポイントリストを取得
if (y % 2 == 1) {
x = 1.0 - x;
}
// Y値が奇数の場合、X値を反転
float ind = rint((len(pts) - 1) * x);
// X値に基づいてプリミティブ内のインデックスを計算
f@ind = ind;
// 計算したインデックスを属性 "ind" として保存
f@sort = ind + y * 1000 + prim % 2 * 0.5;
// インデックス、Y値に基づく重み、プリミティブの偶奇を加算して並び順を生成
ここではまず、現在のポイントから最も近いPrimitiveを探し、そのUV座標を取得します。そして、Primitive番号を2で割った結果を基にY値を設定し、Y値が奇数の場合はUV座標のX値を反転させます。
その後、UV座標とPrimitive内の点数を用いてインデックスを計算し、そのインデックスを属性indに保存します。最終的に、インデックスやY値、プリミティブ番号の偶奇に基づいて独自の並び順を属性sortとして生成します。
まとめ
以上限定的な用途になってはしまいますが、自分が利用する機会のあった点のソートの方法を記させていただきました。だいぶニッチな内容かと思いますが、どなたかの役に立つことがあれば幸いです。
HIPファイル
この記事で説明しているファイルか下記URLからダウンロードできます。