本記事はHoudini Advent Calendar 2020の7日目の記事となります。
はじめに
今回の記事は、テクニカルな内容というよりは、イギリスの大学の建築の授業でHoudiniを使った時のお話になります。そういった内容に興味がある方は読んでみてください。
Houdiniを使った建築+生物デザインの授業
今年の10月から、機会がありイギリスのバートレット建築学校で、リモートでHoudiniを使った授業をさせていただくことになりました。バイオロジー+建築に特化したコースの大学院生たちが生徒で、コンピューターを利用したデザイン、特にコンピュテーショナルデザインを課題を通して教えるという内容の授業を自分ともうひとりの先生の二人の体制で教えるというものです。最終的にはそれぞれの生徒たちに作品を作ってもらい、動画で発表して様々な先生から講評を受けて採点されるという、いわゆる設計スタジオの授業と似たような形式の授業です。一般的な建築のデザインの授業と違うのは、バイオロジーの考え方も視野に入れつつ建築となりうる空間をデザインするというもので、バイオロジカルなシミュレーションをすることが必須という前提条件があるところです。
そして、バイオロジカルなシミュレーションを行い、空間に昇華するメインのツールとしてHoudiniを採用しているということで、それだけでもこれは面白そうな授業だとその話を聞いたときに確信に近いものがありました。バートレットでもこのような授業は結構先端的で、前例があまりないらしく、授業の組み立ても一から行っていく必要があるということで、もう一人の先生と次のような流れで授業を行なっていくことにしました。受講する生徒たちはすでにHoudiniの基本的な操作やレンダリングはある程度できる前提で、今回シミュレーションをするにあたって必須となるSolverやVEXの知識や経験自体はまだあまりないという状況からのスタートです。
まず授業自体のテーマとしてEmergence(創発)というキーワードが設けられました。創発とは、局所的に生じた複数の要素による比較的単純な相互作用の複合によって、それぞれの要素の単純なルールからは予想できない複雑なふるまいをみせることを意味してます。そのキーワードを元に、コースを大きく3つのタームに分けて、それぞれのタームで授業内容をステップアップさせていく形にしました。
-
ターム1: 創発というキーワードの元、6つのテーマを決めてそれぞれのテーマに対するHoudiniを使ったシミュレーションのチュートリアル
-
ターム2: 6つのテーマから各生徒に好きなテーマを1,2個選んでもらい、授業で教えた基本的なシミュレーション手法を拡張して新たな発見をしてもらう
-
ターム3: 拡張したシミュレーション手法を用いたプロセスや結果から想像できる用途を持った空間をデザインする
この授業自体は現在この記事を書いているタイミングでちょうどターム2に入ったところで、既に生徒からは面白いアイディアが色々出ている中ではありますが、今回の記事ではターム1で行った6つのテーマに沿ったシミュレーションの内容について書いていきたいと思います。
創発に関する6つのテーマ
創発と聞いてもあまりパッとイメージできないかもしれなちですが、コンピュータを使った創発に関するシミュレーションというのは実は古くからあって、例えばGame of Lifeというセルオートマトンをベースとした人工生命的なシミュレーションは、グリッドの各セルに対してその近傍のセルの生死の数に応じて次のタイミングで生きるか死ぬかという局所的なルールの複合で構成されているシステムですが、それが結果的に全体として複雑な生死の模様を生じさせるというわかりやすい創発の例だと思います。
ターム1では、そういった創発の種類を一通り生徒たちに知ってもらうことを目的に、全部で6つに創発的な振る舞いをカテゴライズし、一個一個をHoudiniで実際に実装してみるという内容の授業を行いました。その6つにカテゴライズしたものが以下の通りです。
- Fractal (フラクタル)
- Swarm (群衆)
- Reaction (反応)
- Parasitic (寄生的)
- Fluid (流体)
- Structural (構造的)
Fractalでは再帰計算により得られる自己相似形状を含んだカテゴリーとなっています。例えばアンマナイトの殻や雪の結晶、ロマネスコブロッコリーや樹木などの形状がこれにあたります。
Swarmでは個々のシンプルな動きが全体で見ると大きな塊として意思をもっているようなものを取り上げているカテゴリーとなっています。例えば魚群や渡鳥の群れ、アリの巣の作られ方やブラジルのファベーラなどがこれにあたります。
Reactionでは化学反応的な振る舞いをするものを含んだカテゴリーとなっています。例えば熱帯魚やシマウマの模様や、ビスマス鉱石のつくられ方、また先ほども紹介したセルオートマトンなどはその例となります。
Parasiticは既存の物体に寄生して成長するようなものを含んだカテゴリーとなっています。例えば船底に張り付いたフジツボや、虫や木に寄生して成長するキノコなどの菌類などがあげられます。
Fluidは力場によって動きを流動的に変化させるものを対象としたカテゴリーとしています。例えば水のような直接的な流体もあれば、磁場のように目には見えないが力場が存在しているようなものも含んでいます。
Structuralは構造的な最適化を行った上で得られるような形状を含んだカテゴリーとなっています。例えば蜘蛛の巣や、風船や折り紙などが例として挙げられます。
これら一個一個のテーマに対して、どんな基礎授業を行なったかをここでは紹介していきたいと思います。具体的にはそれぞれのテーマに対して、基本的な考え方の元となるアルゴリズムや手法を生徒に伝え、その実装方法を教えていったという感じになります。
下準備! フィードバックループとソルバーの基礎
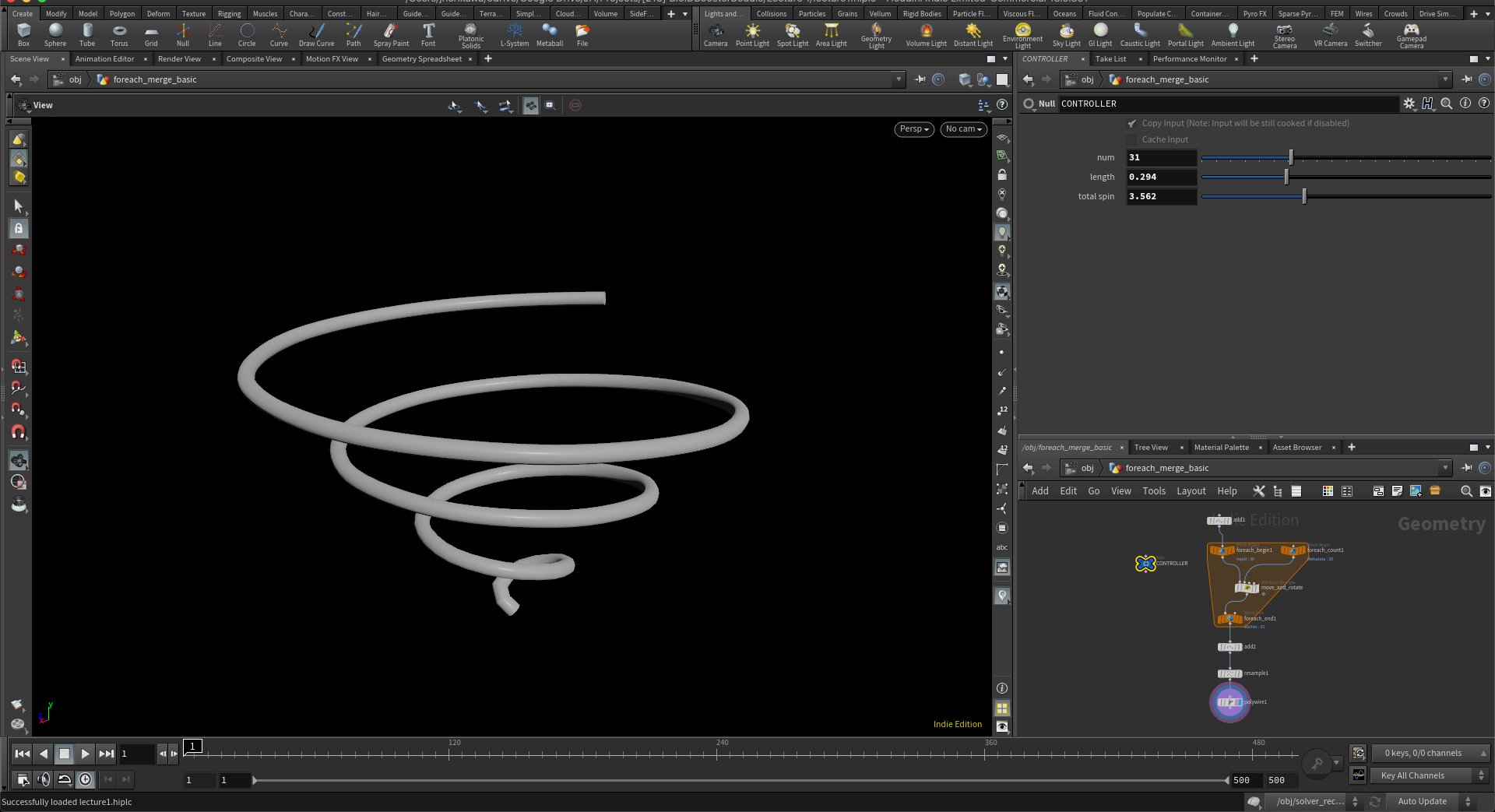
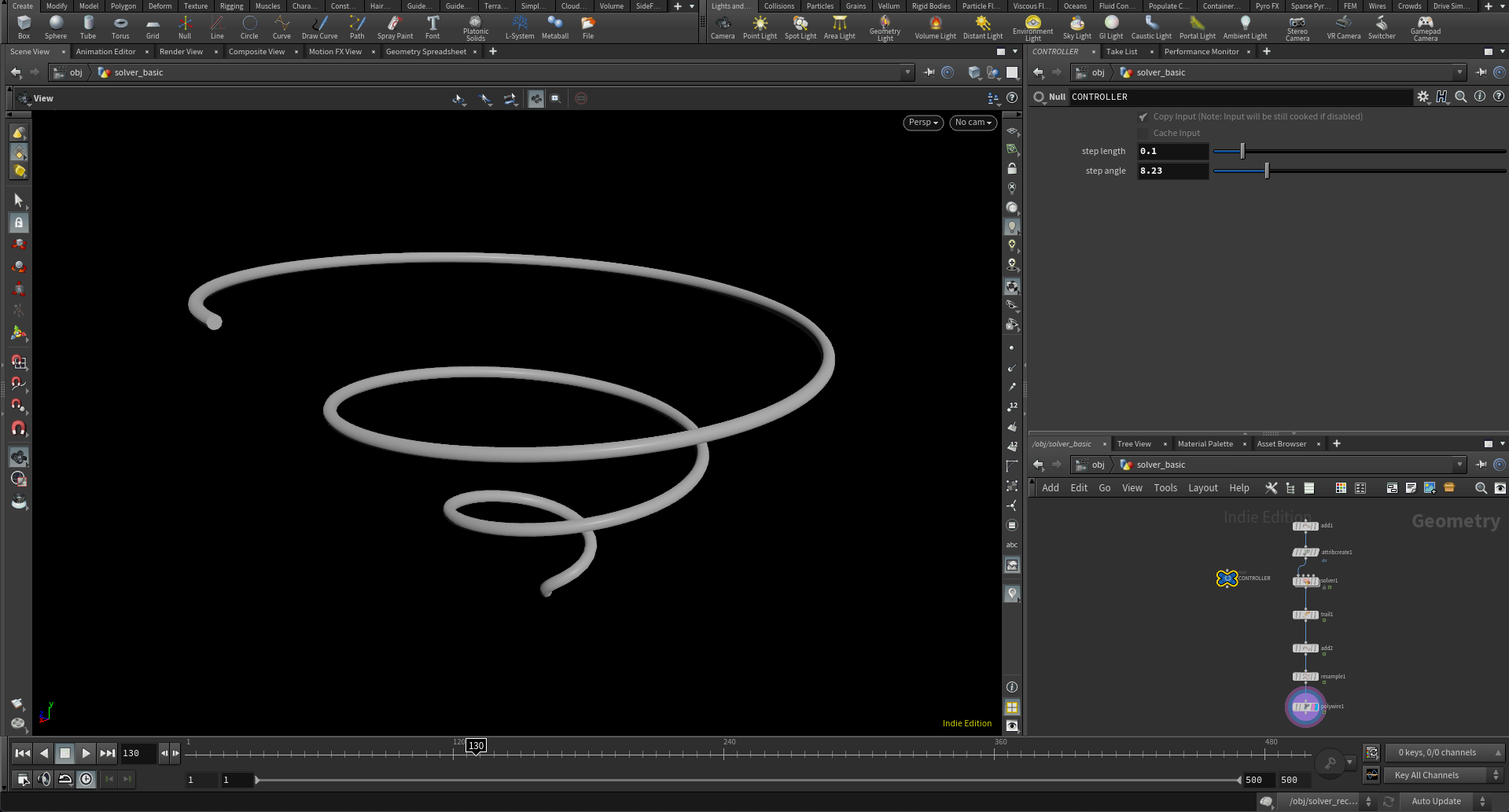
創発系のシミュレーションに必要な最もベーシックな技術として、何はともあれ欠かせないのが再帰計算手法です。Houdiniではご存知の通り、再帰計算のために二通りの方法が用意されています。ひとつはForEachノードを利用した静的な再帰計算を行えるフィードバックループで、もうひとつはSOP Solverを利用した動的な再帰計算です。
まずは練習として生徒たちにこの二種類の手法を、同じスパイラルなワイヤー形状を作るという簡単な課題を出して教えることにしました。これ自体は創発系シミュレーションとは違いますが、根底に流れる手法はいずれも同じなので、ForEachを使った静的なフィードバックループ、あるいはSolverを利用した動的なフィードバックループを自由に使えるということはかなり重要な点になります。あと今回の授業は最終的に動画として書き出さなければいけないので、どちらかというとSOP Solverの使い方を早い時点でマスターしてもらう必要がありました。
再帰計算の基礎 Fractal / フラクタル
アルゴリズム・手法例: L-System
再帰計算の基礎ができたところで、まず6つのカテゴリーの中で一番基礎的とも言えるフラクタル的手法に触れてもらうことにしました。フラクタルとは局所的な形状と大局的にみた形状に相似性が観られるような形状の総体を指すことが多いですが、そういった自己相似形と呼ばれる形をつくる手法として、今回は最も有名な手法の一つであるL-Systemに注目することにしました。
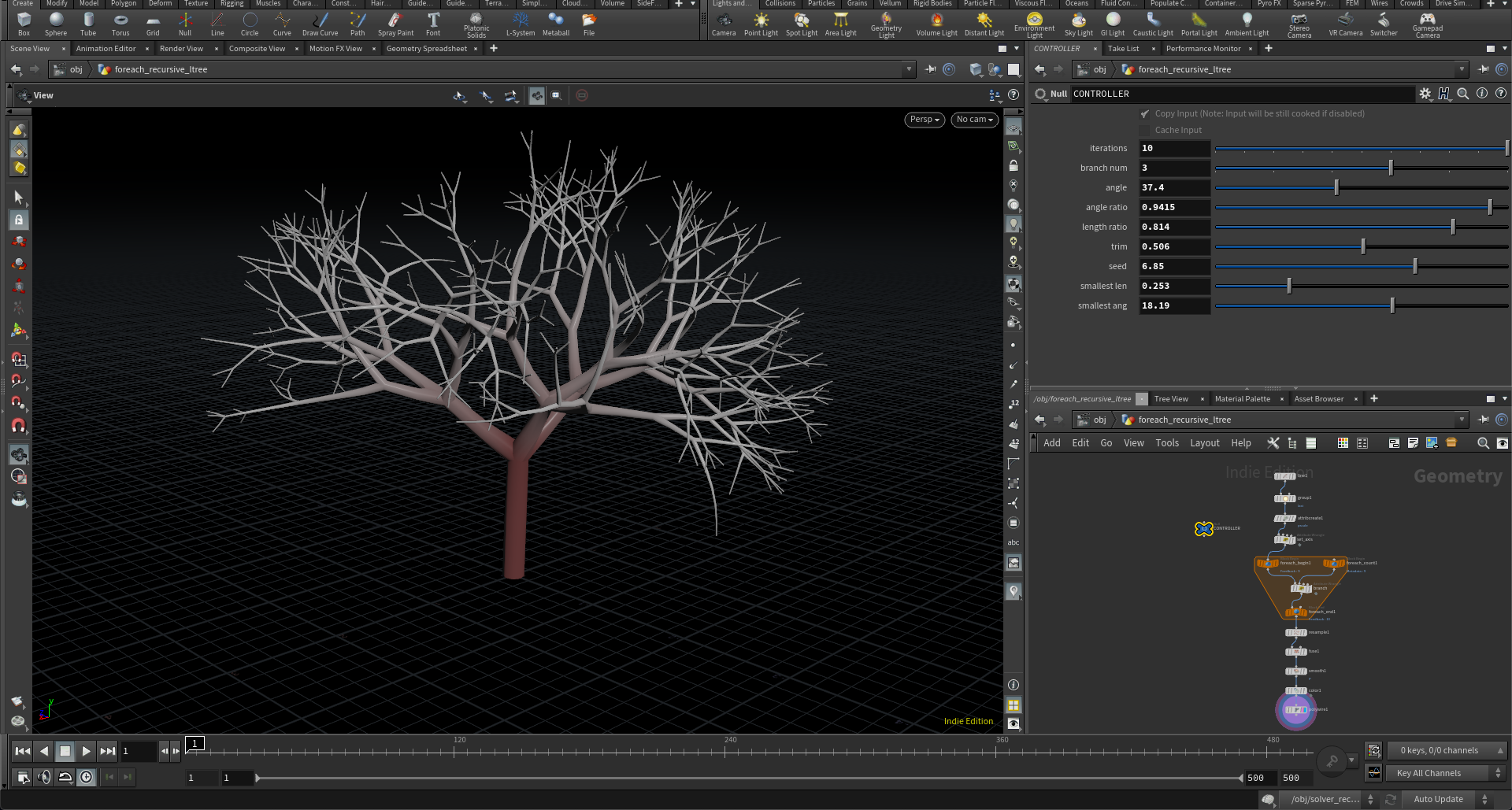
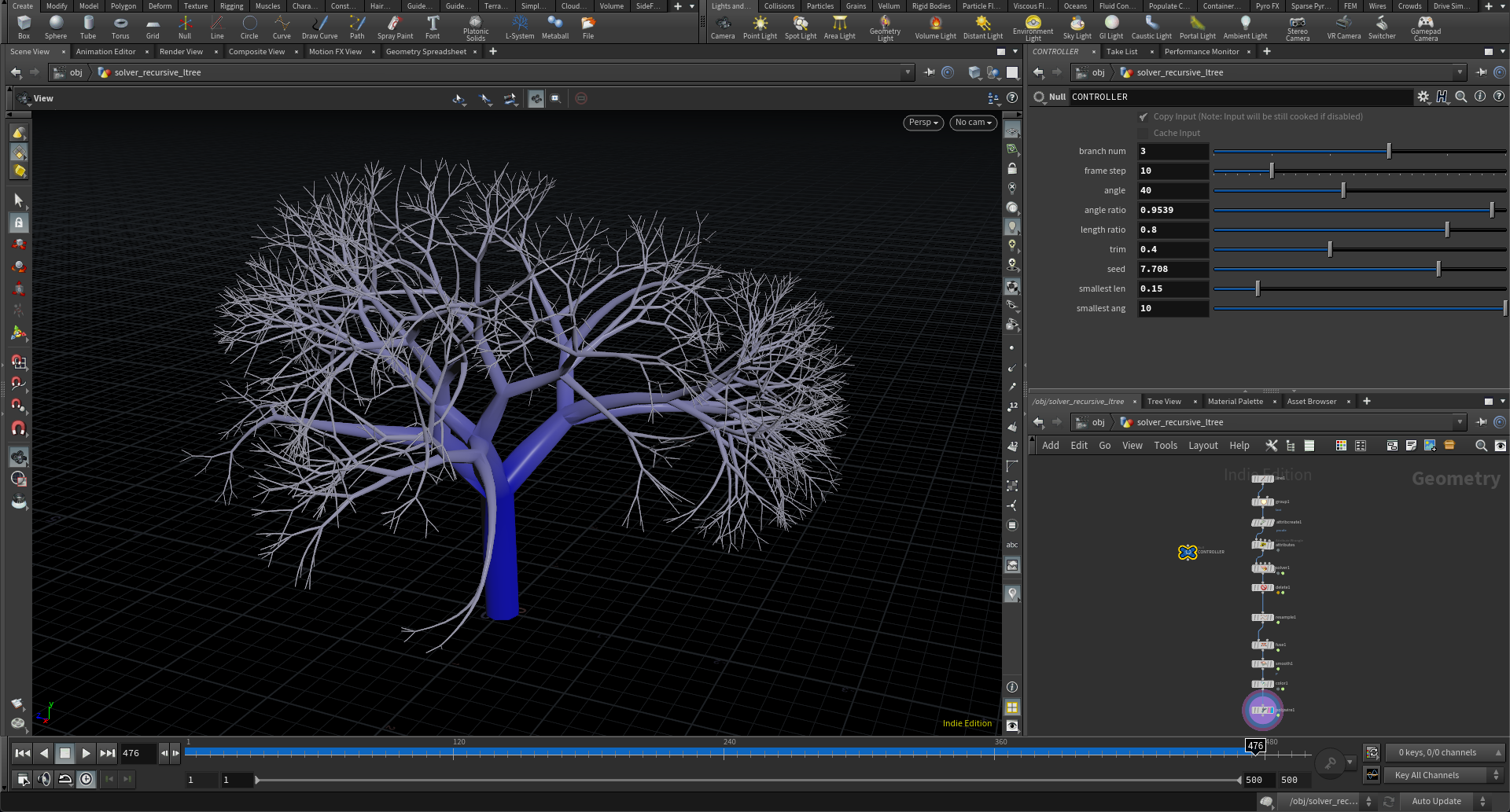
L-Systemのアルゴリズムは主にコンピュータ上で樹木を再現する手法として利用されることが多いですが、考え方の基本としては成長の過程を世代で表現し、親の世代から子の世代が生まれるときに親のDNAを引き継ぎつつそこに多少の変化を加えることで形状を積み上げていくという考え方に基づいた手法です。という考えのもとであれば、別に樹木に限定する必要はないのですが、例としてわかりやすいのでここでは樹木をL-Systemで作るという方法を教えることにしました。
Houdiniには既にL-Systemそのままの名前のノードがあって、それを利用すれば簡単にフラクタル形状を再現することは可能なのですが、今回の授業の最終的な目標としては学んだ手法を自分で拡張し、またそれを利用したアプリケーションを考えるという点から、L-Systemノードをそのまま使うのでは自由度が限定されると考え、ForEachノードやSOP Solverを使っていかに1から自分でルールを組み立てていくのかという点にフォーカスを当てて教えることにしました。
一個失敗したなと思ったのは、基本的なフラクタル形状として樹木ならわかりやすいかなと思ってこの形状を作ることにしたのですが、同じアウトプットが作れるならL-Systemノードをそのまま使ったほうが良いと思ってしまう生徒もいたことです。長期的に見てそのL-Systemのロジックを自分で組めるほうが拡張性は高いことが伝わりきっていない、L-Systemノードに頼りすぎると後々複数の創発的手法を組み合わせるときに足かせになり得るという点が感覚としてまだ持てないのは始めたてであれば当然のことで、それを伝えきれなかったなと多少後悔しました。少なくとも、樹木形状ではないフラクタル形状で例を作ったほうが良かったかなとは思いました。
予測を裏切る化学反応 Reaction
アルゴリズム: Cellular Automata / Gray-Scott
次に教えたのがReactionというカテゴリーに分類した先にも少し紹介した化学反応的なシミュレーション手法です。大きな考えかたとして、まず限定的な空間が用意されていて(2Dや3Dグリッド、メッシュなど)、その空間の上の各点や各面が隣り合う点や面の状況に応じて自らの状況を変化させていくという手法をまとめてここではReactionとしています。
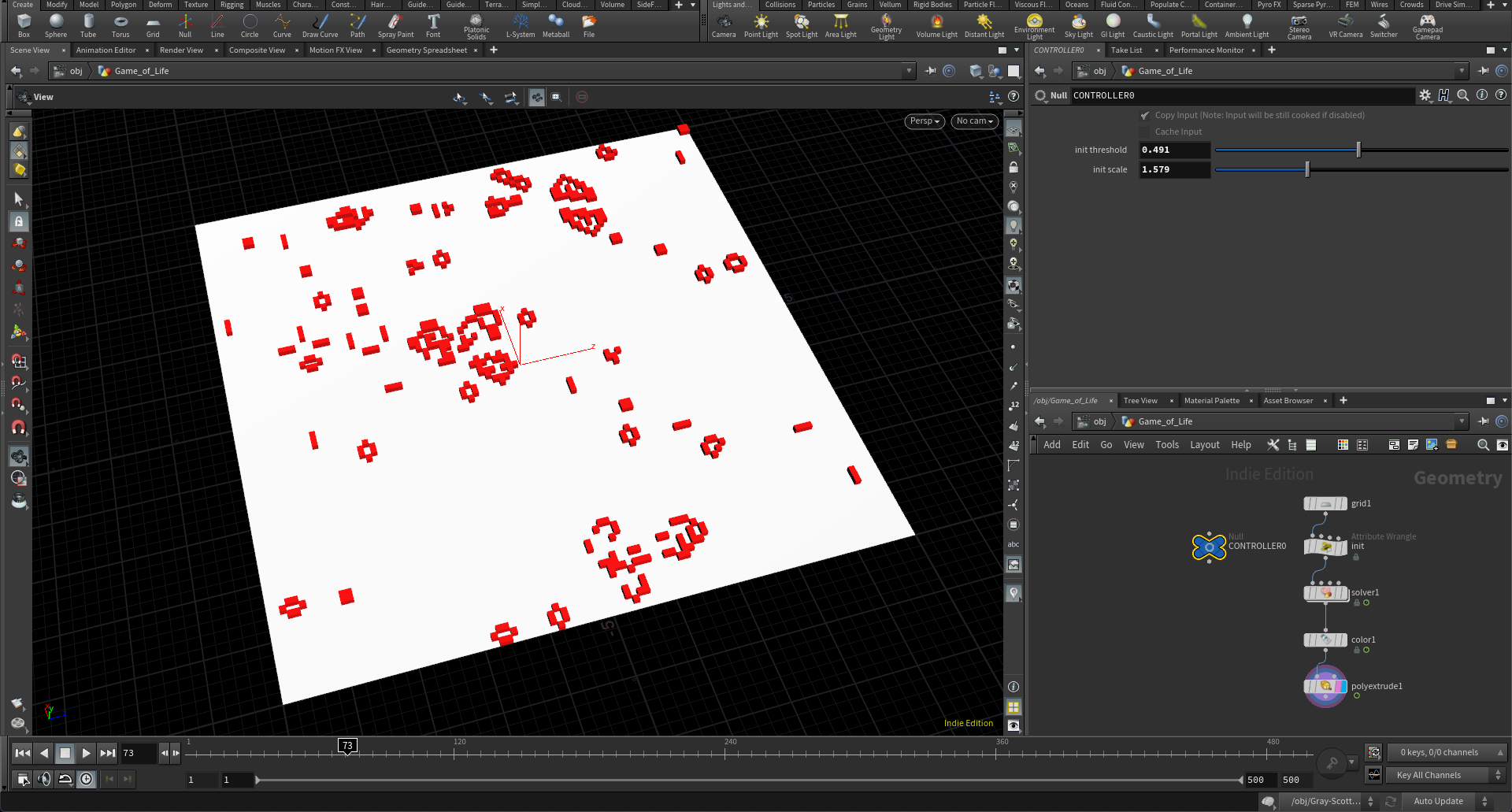
その系統のシミュレーション手法として有名なものの一つがセルオートマトンと呼ばれる、先程Game of Lifeの例でもでたグリッドセルなどの近傍の状況に応じて自らの状況を変化させるというものです。そしてその考え方のさわりとして、まずはGame of Lifeの実装から始めるのはとてもわかり易いと考えたため、二次元的な模様を作るものではありますがHoudiniでどう実装するかというところから教えることにしました。
ルール自体はとても単純なもので、各グリッドのセルに注目して、そのセルの近傍の生死の状態をみて、次の自分の状態を決めるという形になるわけですが、Game of Lifeの場合そのルールが単純すぎる故、初期のグリッド上のセルの生死の状況によって最終的に出来上がる模様が結構変わる可能性があり、化学反応系のシミュレーションのさわりとしては面白いですが、なかなかここから拡張していくのは難しそうだなという印象を持つアルゴリズムです。考えられる拡張性の方向性としては、グリッドを三角形とか六角形、あるいは三次元グリッドにしたり、隣あるセルとのリアクションのルールを既存のルールから改変してみたりということが考えられますが、なかなかそのパラメータの調整がピーキーである(ちょっとルールを変更すると模様にならずにすべて死に絶えてしまう)という点があります。Game of Lifeを発見したConwayはきっとこのルールを見つける過程でいろんな死にルールを作って来たんだと想像させられます。
何はともあれ、リアクション系のシミュレーションのベースの考え方はこれで得られたことにはなるので、少しその考えを拡張してより複雑な模様を描くようなシミュレーション手法も教えることにしました。今回ピックアップしたのはいわゆるチューリングパターンと呼ばれるシマウマや熱帯魚の表面にみられるような模様を再現するもので、Reaction Diffusion(反応拡散系)とよばれる化学反応的なアルゴリズムの一種であるGray-Scottです。
基本的な考え方はGame of Lifeと一緒で、近傍のセルの状況に応じて自身の状況を変化させていくわけですが、Game of Lifeの場合、生か死かという二通りの状況しかなかったのに比べ、このGray-Scottのアルゴリズムでは一つのセルの中に二種類の反応系の値が入っていて、その値を浮動小数点数として表現するため状況の変化がより複雑になります。また、この二種類の値が食い合うような形で値をアップデートしていくことで、模様があたかも成長していくようなシミュレーションを行うことができるようになります。あとはその二種類の値の強弱のパラメータ(かんたんにいうとですけど)を変化させることで、多様な模様を作れるようになるというものです。
ただこれも非常に有名なアルゴリズムの一つで、散々やり尽くされたものではあります。せっかくHoudiniを使うからには多少の新しさは持ち込みたいと思い、通常このアルゴリズムは二次元グリッド上で動くものですが、それを多少改変し今回は独自に三次元サーフェースでも使えるような形のものを教えることにしました。また、特定の位置に異なる模様を描くといった手法も加えて教えることで、コントロールが難しそうなアルゴリズムでも拡張性の幅を伝えることに注力しました。
いずれにしても欲しい模様を得るためのパラメータの調整が難しいことは変わりなく、すでに発見されているパラメータを利用する分には使いやすいですが、新しいパラメータを発見しようという気に学生たちがなかなかならず、あまりこの手法をメインで使いたいという人がいなかったのは残念ではあります(個人的にこのアルゴリズムがどう拡張されるのかみてみたかった)。
群衆を操る Swarm
アルゴリズム: Flocking
次に、Swarmというカテゴリーの元、群衆のシミュレーション手法を教えることにしました。群衆のシミュレーション手法自体はゲームでもAIとしてよく使われるものの一つかと思いますが、その中でもこの授業ではまずは基本中の基本、Craig ReynoldsによるFlockingと呼ばれるエージェントベースのシミュレーション手法の実装の仕方を教えることにしました。
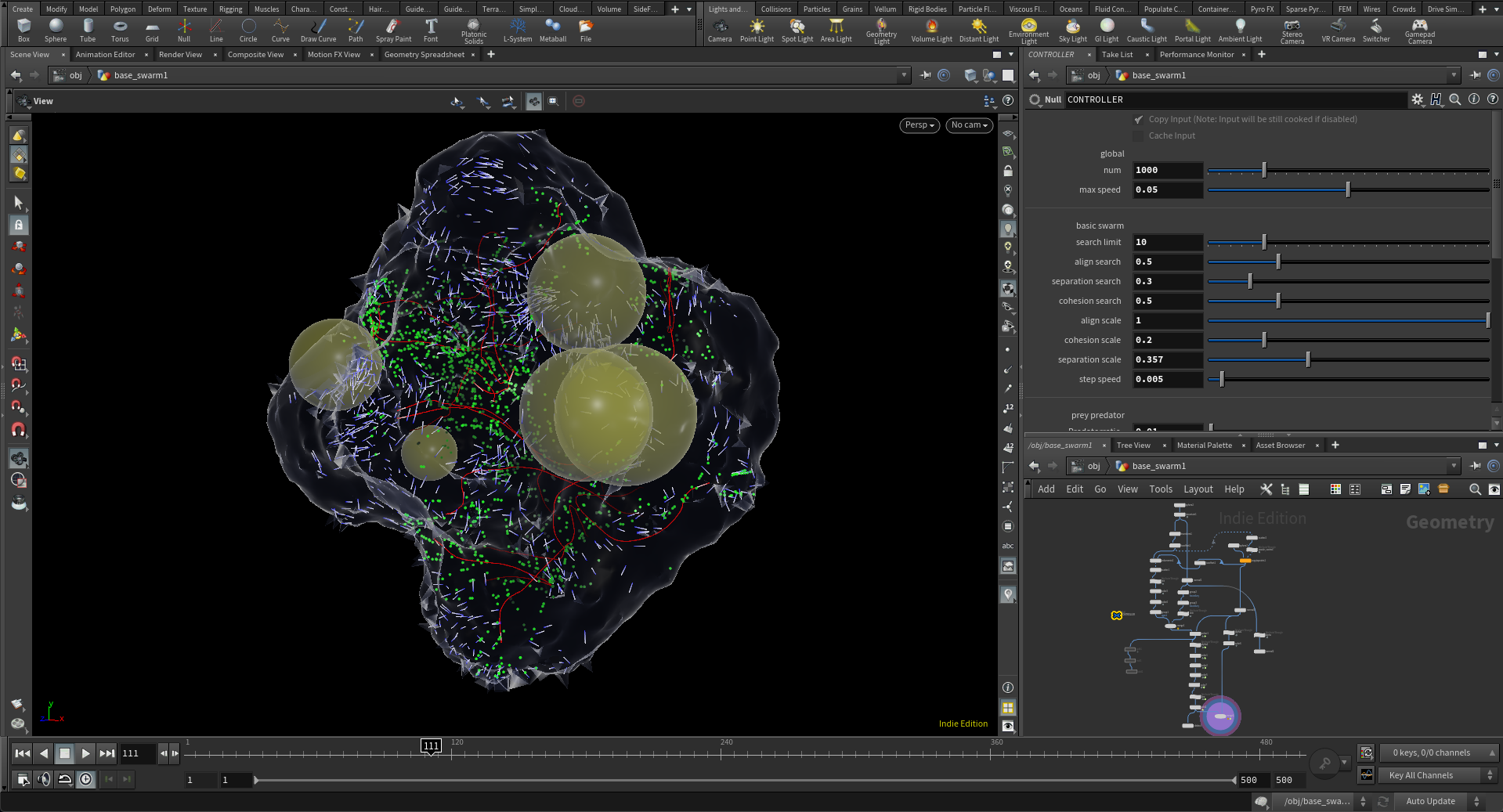
このアルゴリズム自体は80年代後半に紹介されたもので、空間に複数のエージェントと呼ばれる要素を配置し、個々の要素にそれが動くためのルールを記述する形になっています。具体的には各エージェントから、それに近い範囲にあるエージェントを見つけ、その近くにいるエージェントとの関係性を力(ベクトル)として記述します。Reynoldsは基本的な力として近くのエージェントと同じ方向をむくAlignment、近くにいすぎるエージェントから離れようとするSeparation、遠くにいるエージェントに近づこうとするCohesionの3種類の力の組み合わせによって各エージェントの動きをコントロールします。この個々のエージェントの単純なルールが、全体として動きを見たときにあたかも魚や鳥や虫が群れをなして移動しているように見えるという創発系シミュレーションのわかりやすい例の一種です。
実装の仕方自体はウェブで検索すればいくらでも出てくるので、今回はHoudiniという3次元空間を記述するのに適しているツールを使い空間デザインに昇華しなければならないということで、ベースのFlockingのシミュレーションに加え、Houdini以外でやろうとすると少々面倒くさいような要素も加えて教えることにしました。例えば多くの場合、Flockingのシミュレーションの領域はボックス形状であることが多いのですが、バウンダリ形状を自由曲面にしても、そのバウンダリにあたったらエージェントが反射して反対の方向を向くような力を加えるという方法を教えることにしました。
またそれに加え、複雑なルールを自分で記述できるようになるために、次のようなオプションもおしえました。
- 障害物オブジェクトを避けるような力をエージェントに加える。
- 追うもの、追われるものという二種類のエージェントのタイプを作る
- 追われるエージェントが通った道にフェロモンを落とし、そのフェロモンに追うものは近づけない
- 追うものが通った後には軌跡が残る
- エージェントがバウンダリ(壁)に当たると壁が外側に拡張される
いずれもルールの記述の仕方自体は単純で、ポイントは小さく積み上げたこういったルールが、全体でみたときに複雑な様相を見せるということです。箱庭的にエコシステムを作っていると考えたら面白いかもしれません。
考え方は先のReactionとにている部分もあるのですが、ルールの記述の仕方が明快で、個々のエージェントに関しては動きが予想しやすく、また全体的には面白い動きを作りやすいということで、人気のカテゴリーの一つです。
ホストとゲストの関係 Parasitic
アルゴリズム: Space Colonization
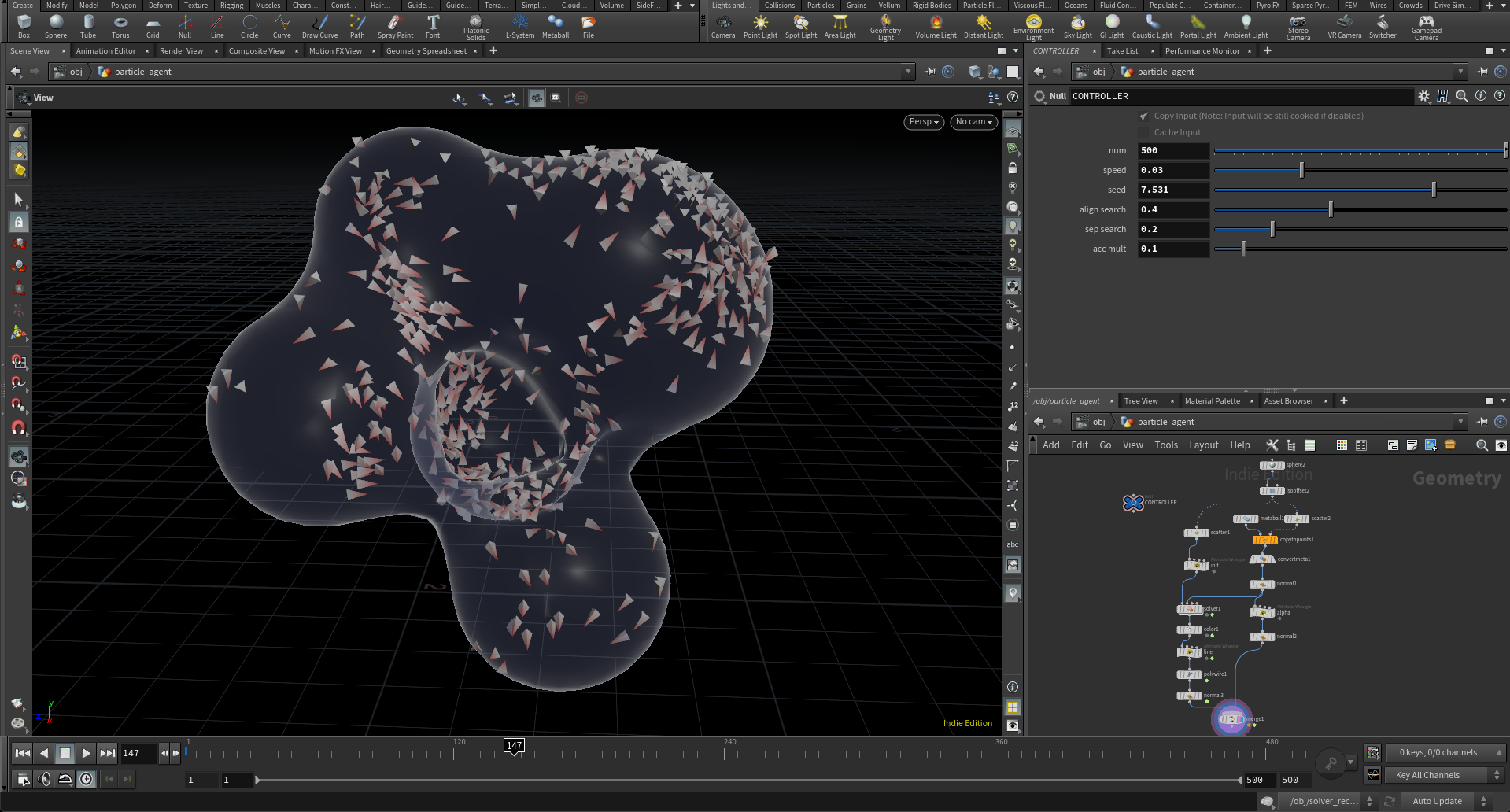
Parasiticというカテゴリーでは既存のオブジェクトに寄生するシミュレーションを扱うことにしました。ただ具体的にそのためのアルゴリズムが直接的にあるかというとそういうわけではなく、与えられたオブジェクト自体がシミュレーションの拘束条件の一つとして使われた場合、いずれの手法を用いてもParasiticと呼ぶことが可能です。今回は点群の中を餌を食うように這って樹木的に成長するネットワークのシミュレーション手法であるSpace Colonizationに注目して、ホストとの関係をアルゴリズムに加えることでParasiticの一つとして扱うことにしました。
Space Colonizationでは粘菌が成長するようにある点から周辺に散らばった餌となる点群を見つけ、その方向に移動し、移動し終わった後に近くの点を食うことで成長をしていくモデルとなっています。その点群の配置をまずは寄生先のホストとなるオブジェクトに関係付けるところから環境を作り始めました。あとはモデルの曲率に応じて粘菌が這うスピードをコントロールできるようにしたりなど、ホストとゲストの関係の記述をしていくことがこのカテゴリーではメインに考えることにしました。
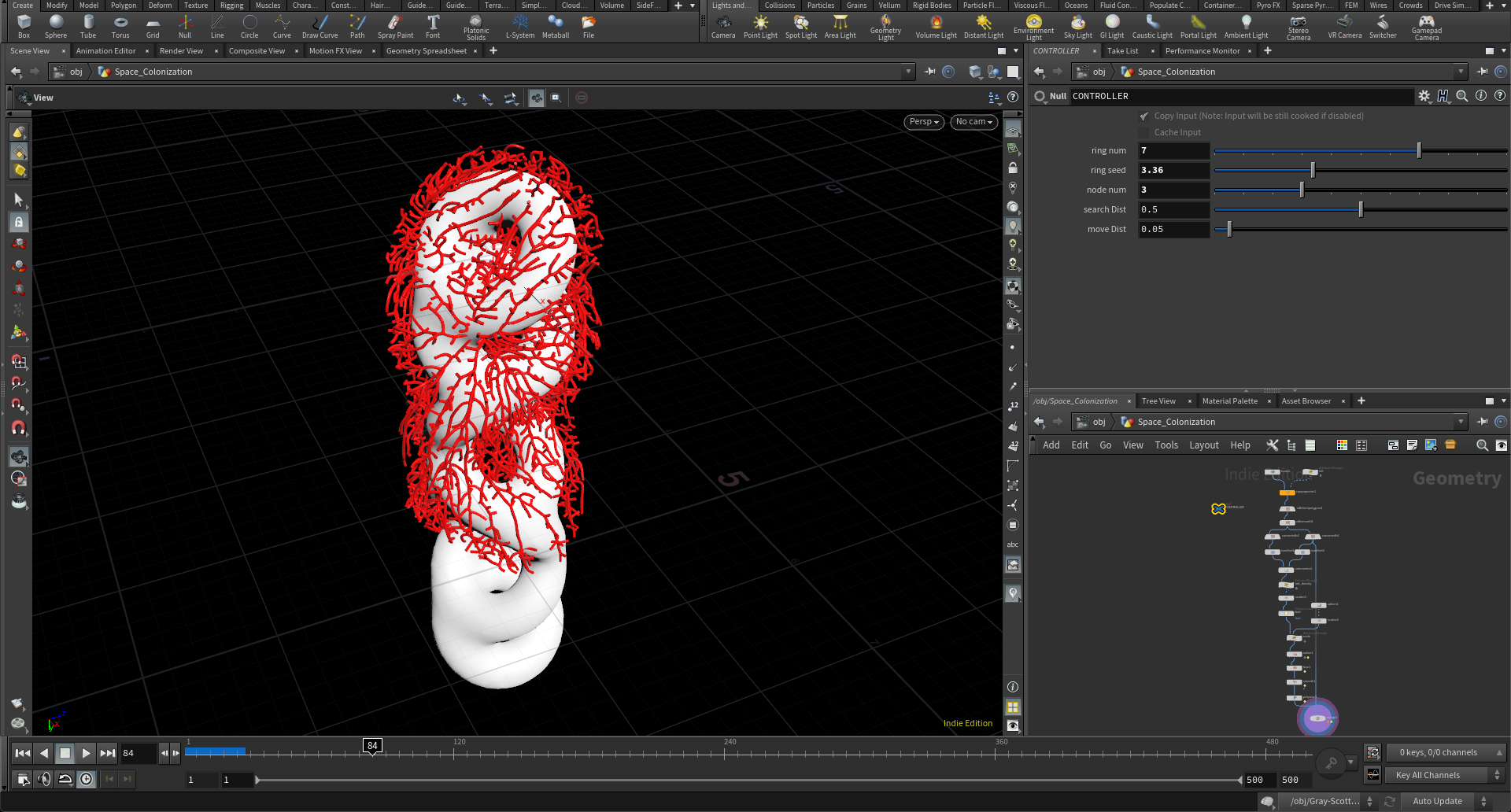
Space Colonizationのアルゴリズムをアップデートし粘菌(ゲスト)と寄生先(ホスト)の関係を記述
なかなか面白みのあるカテゴリーかとは思うのですが、ビジュアルとして粘菌のようなネットワークを見せてしまったが故に、学生たちはその背景にあるロジックよりもアウトプットとしてのビジュアルだけに注目してしまいがちなのが難しいところです。重要なのはプロセスであり、そこから得られるビジュアルは多様にできるということをもっとわかりやすくしないといけないのだなと感じました。
力場をコントロールする Fluid
アルゴリズム: Noise / Navier Stokes
このFluidというカテゴリーでは主に流体の動きに関係のあるようなシミュレーションをピックアップすることにしました。HoudiniはVFXの業界で強いツールということもあって、流体系のシミュレーションに関してはOut of the boxでかなりの種類のアルゴリズムを試すことができるため、それをそのまま使うということも十分ではあります。また、それぞれのDOPソルバーの中でコードも記述できるので、それなりに拡張性もあるといういいとこ取りができるのが素晴らしいです。
ただDOPシミュレーションは物理的に正しく見えるように組まれたアルゴリズムであることが多く、それ故に計算コストが高くなりがちなところがあるため、今回はやはりSOP Solverを使って最低限の流体のシミュレーションの実装を通じて、流体シミュレーションの核となる部分を学んでもらうことにしました。またそうすればそれを既存の使われ方とは違うかたちで利用することも可能であると気づくことに期待をこめて。
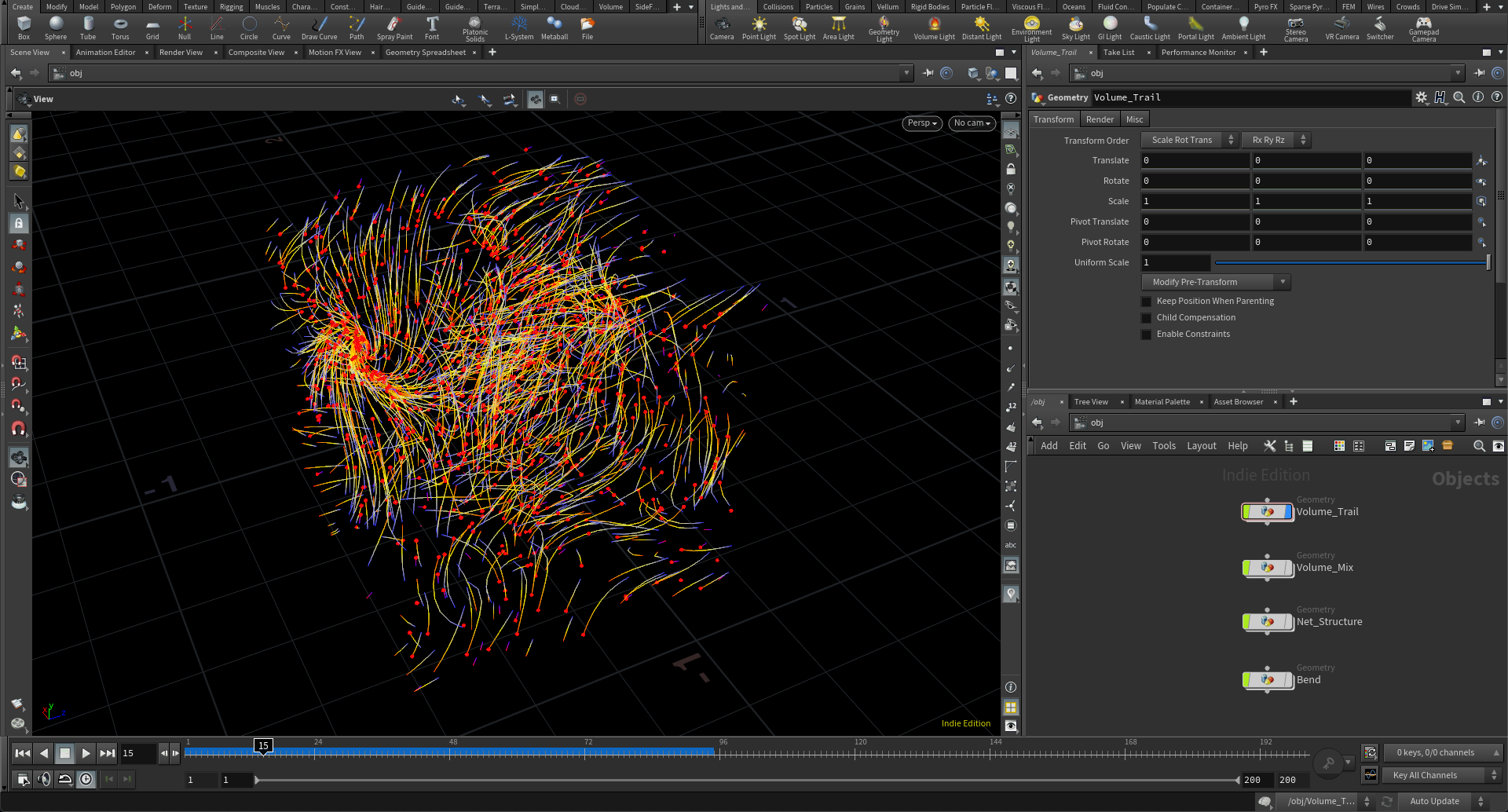
まずは流体シミュレーションの基本的な考え方として、力場を作り、その力場に沿って粒子を動かしてみるというところからはじめました。力場自体はベクトルVolumeとノイズ関数の組み合わせで作り、時間に応じて力場が変化するようにしておき、その力場によって粒子の動きが影響されるというものです。この考え方自体は例えばSwarmのカテゴリとも相性がよく、エージェントの動きをある力場によってコントロールするときのアイディアにも使えるものです。
ただ力場をノイズ関数で動かすだけだと、自然の動きからかけ離れているので、力場のコントロール自体をより自然な流体シミュレーションのそれに近づけるためにNavier Stokesの方程式も教えることにしました。これは流体の動きを記述する方程式で、流体力学でよく使われているシミュレーションに利用可能な方程式です。具体的にここで教えたのは、グリッド上の空間を用意し、そこにベクトル場のベースとなる点群を配置して、そのポイントに速度ベクトルや粘性などの属性を与えて、外から力を加えたときの速度ベクトルを計算するというものです。
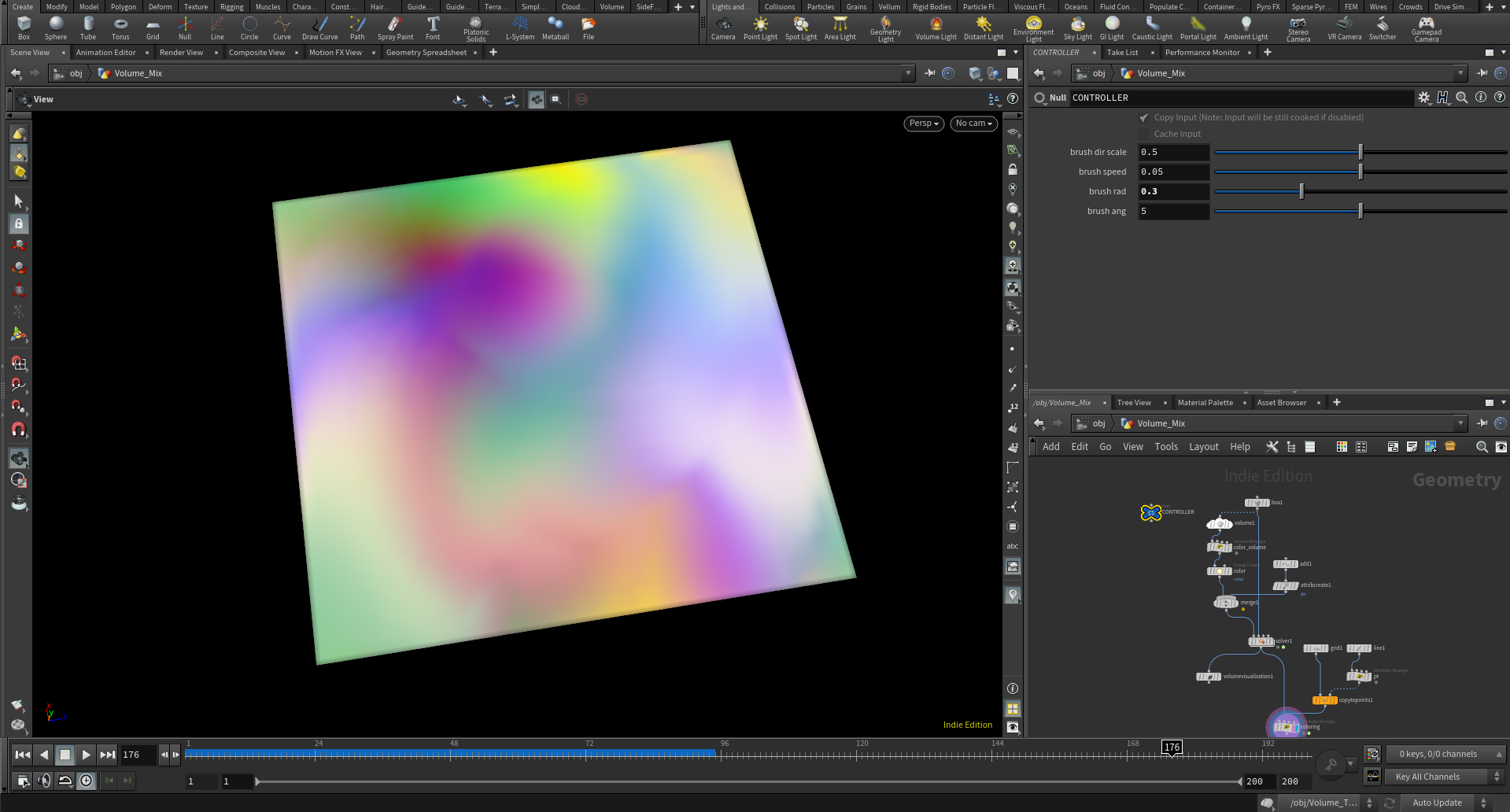
Navier Stokesをベースに絵の具の混ぜシミュレーションを行う
ノイズ関数はまだわかりやすいから良いのですが、Navier Stokesなどになると偏微分方程式などが出てくるため、そこのベースの知識がない学生にはだいぶ辛かったかもという印象でした。デザインの武器として使うには他の手法と比べてベースの知識が多く必要であるため、拡張もしずらそうという点に気づきました。遅くてもDOPでやったほうが良かったのかもしれません。(ベースの考え方だけでもわかってくれていたらいいな)
構造的最適化の末に Structural
アルゴリズム: Stretching / Origami Folding
最後のカテゴリとして選んだのがStructural(構造的)です。主に個々では物理シミュレーションベースの計算を利用して形態を作るということを考えたのですが、これに限っていうとSOPですべてやろうとすると膨大に面倒くさい準備をしなければいけないという点があり、またそれ以外の方法でSOP Solverだけで実現する方法は難しそうだったので、物理シミュレーション系に関してはVellum Solverを代わりに使うことを提案しました。
Vellum SolverはSOPの中で物理シミュレーションのコントロールすることが可能である点が素晴らしく、またちょっとしたトリックを使えばSOP Solverで作った別のシミュレーションとも組み合わせることができるので、物理ベースのシミュレーションを行いたいならこれは非常に便利です。1からSOPでパーティクルベースの物理シミュレーションを作ったことがある身としては、Vellumはやはり高級な機能が詰まっているだけあって多少の遅さは感じますが、あまり気にならない程度に最適化も十分にされているように感じます。むしろ1から自分で実装する手間を考えたら気が遠くなりそうです。
このカテゴリーでは二種類の物理シミュレーションを利用した造形づくりを教えることにしました。一つは基本的なワイヤーのストレッチのシミュレーション、そしてもう一つは折り紙などに応用できそうな折(曲線折)のシミュレーションです。
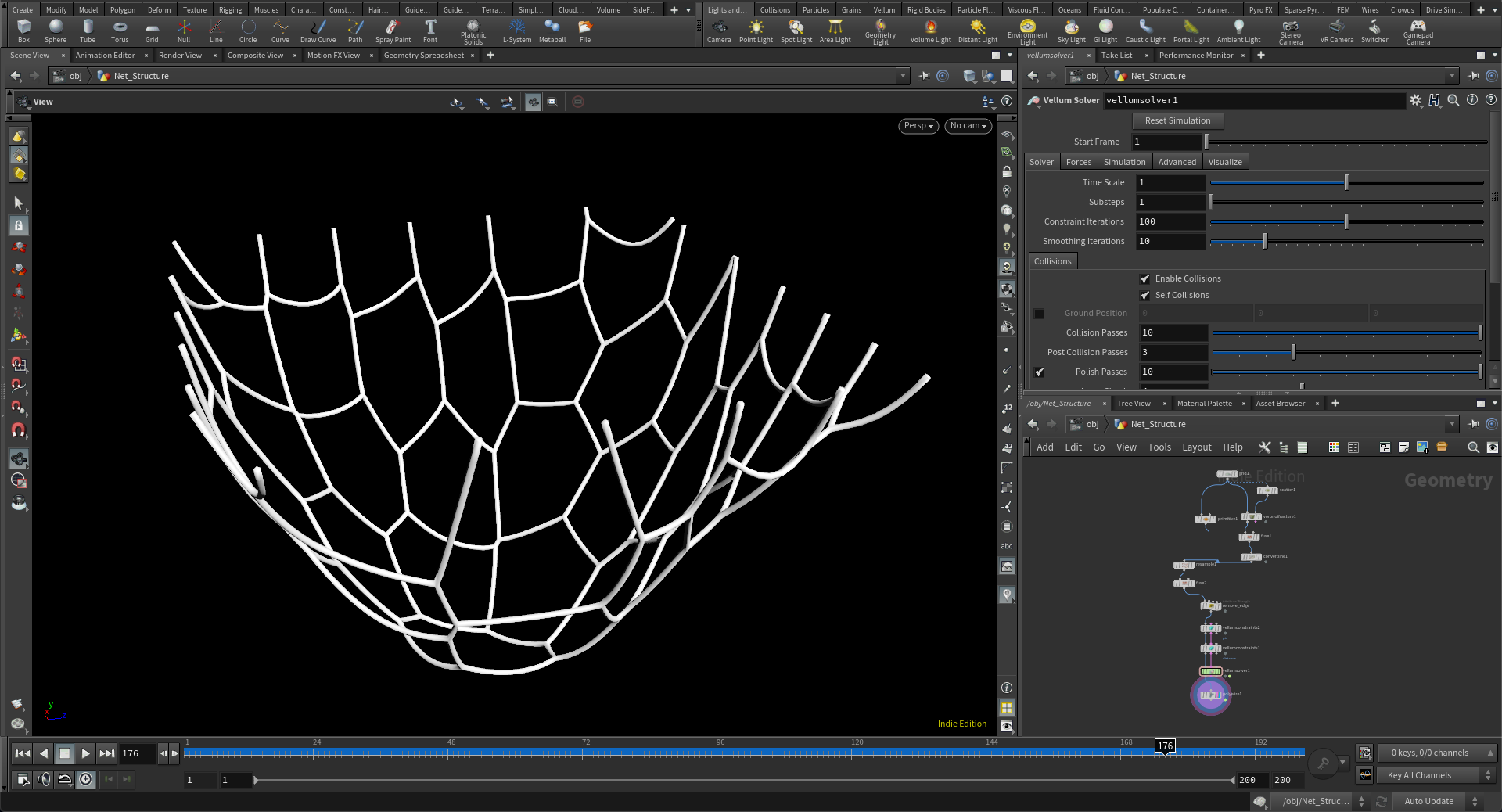
Stretchの拘束をつかったワイヤーのテンションのシミュレーション
折りのシミュレーションなどは拘束条件をカスタムに操作しない限りは実現が難しいもので、そういうった点で拡張性の可能性は大きく感じる点があります。そしてこういった物理シミュレーションは単体で使うと物理的な挙動を示すだけのものとなりますが、これに先に紹介した5つのカテゴリーのシミュレーションと組み合わせることで、世にみたことのない挙動を作りあげることも可能となります。実際に生徒のひとりはその方向性で現在デザインを進めていて、すでに個人的に大きな可能性を感じているところです。
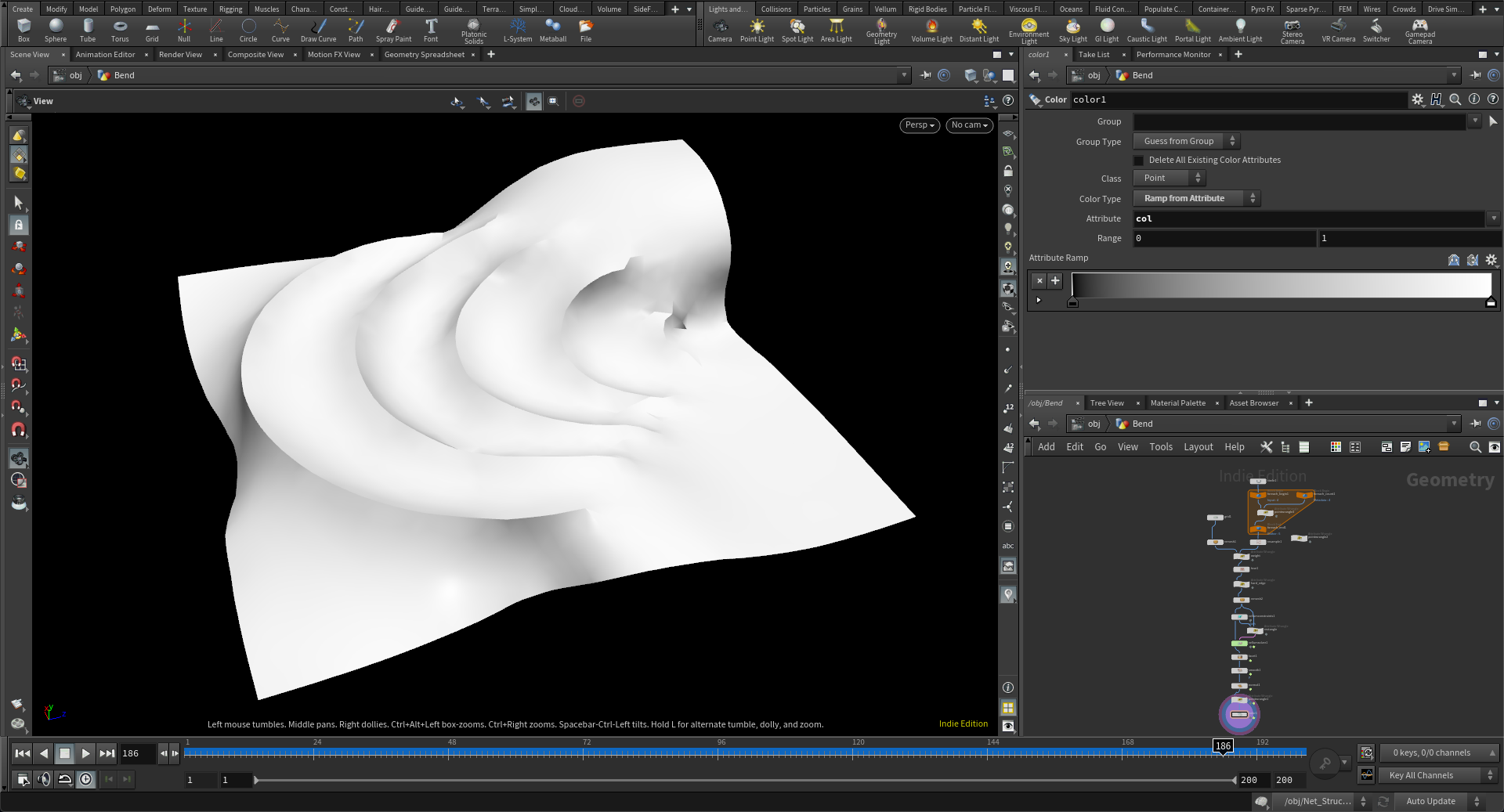
曲げの拘束をカスタムにコントロールすることで折りのシミュレーションを行う
なので物理シミュレーションに関してはその動きのルールがすでにかっちり決まっている分、物理ルールの改変を後からするのは難しいので、拘束条件をカスタマイズするか、他のシミュレーション手法と併用することで創発的な新しい様相を作り上げることが可能かなと感じています。
ふりかえって
まだ授業自体は半分を過ぎたところで、これから個々のカテゴリのシミュレーションを学生が個々に拡張していってそのアプリケーションを考えていくという形になりますが、まず個人的に大学内にこういった授業ができる環境(+周辺の理解)があるという点がなにより素晴らしいなと思いました。これが実利的・実務的になんの役に立つかわからないという人が多く出てきそうな気もしますが(実際学校内でもそう思う人は多いらしいですが)、ここで説明していることは自然を人工的に記述基本的な考え方ばかりで、直接的にそれを使うアテがあるかどうかは関係なく、その上のもっと複雑なレイヤーの事象を理解する上では最低限持っておきたい、そして可能であれば自分自身で記述したいものだと思っています。建築に限ったことではないと思っていますが、もし建築のデザインに興味がある学生さんなどが読んでおられる場合は、今非常に熱いトピックであるということだけ伝えさせてもらって、この記事を締めたいと思います。
そして今回使ったHoudiniというツールは、現段階でシミュレーションベースの空間デザインを行うにあたってベストな選択であると断言しておきたいと思います。日本の大学の建築教育でも使われるようになるといいな!(そしたら呼んでね)
Houdini Advent Calendar 2020の8日目は @70_cg_art さんの「HoudiniとPySide2で始めるGUIツール作成」です。