はじめに
この記事は Houdini Advent calender 2019 の22日目の記事です。日をまたいでしまいました、ごめんなさい!
テーマは以前から狙っていたものがあったのですが、週末でできるかなと思ったら思った以上に苦戦してしまいました。
本記事ではポワンカレディスクと呼ばれる双曲幾何学のモデルに注目して、その上にタイリング模様をHoudiniで作って見るという試みの過程を説明しています。
双曲幾何学とポワンカレディスク
普段ぼくらが慣れ親しんでいる幾何学の空間はユークリッド幾何学と呼ばれるもので、二次元や三次元空間において直線がまっすぐに表現される空間です。
それとは異なり、簡単にいうと曲がった空間における幾何学が双曲幾何学と呼ばれるものです。この空間ではおなじ直線でも人の目から見ると曲がっています。
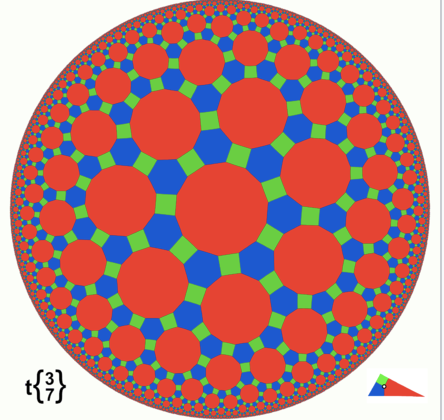
ポワンカレディスクはその双曲幾何学のモデルのひとつで、直線はユークリッド幾何学で言うところの円弧で表現されます。
まだ調べ始めたばかりなので、自分もまだ理解が及んでいないことが多いのですが、このポアンカレディスクのもつ面白い特性の一つにタイリング模様のバリエーションの広さがあります。
タイリング模様において仮に一つの多角形の頂点の数をpとして、その頂点に接する多角形の数をqとします。そのとき、ユークリッド幾何学空間でのpとqのバリエーションは非常に少なく、次の3パターンしかありません。
- p = 3, q = 6 (三角形タイリング)
- p = 4, q = 4 (四角形タイリング)
- p = 6, q = 3 (六角形タイリング)
ユークリッド幾何学では三角形のすべての角の角度を足すと180度でフィックスされているため、このような制限が生まれているわけです。
それに対して双曲幾何学空間での三角形の角度の合計は180度以下の不定な値になり、かつ多角形の角すべての角度の合計は(p-2)*πという不思議な特性を持っています。
これを式にすると
(p - 2) * π / p * q > 2π
となり、さらに分解すると
(p - 2) * (q - 2) > 4
という条件式ができます。これはつまり、この条件式を満たすことができればpとqの値は何を入れてもいいということになります。
WikipediaのUniform tilings in hyperbolic planeというページに行くといくつかの例をみることができます。ユークリッド幾何学では再現不可能な七角形タイリングなどがあります。

より詳しい定義に関しては記事の最後にある参考URLに行って確認してみてください。
Houdiniを使ってポワンカレディスク上にタイリング模様を作る
ではHoudiniを使って、どのように自分がこの模様を作っていったかの過程を説明していきたいと思います。その過程の中で簡単にアルゴリズムも説明していきます。
この記事の内容だけでスクラッチで再現するのは情報が足りないかと思うので、記事の最後にあるダウンロードリンクからファイルをダウンロードして、そちらを見ながら読んでみてください。

前提
前提として、なぜHoudiniでやろうとおもったかという点ですが、アドカレで書くモチベーションとは別に、この作り方を調べているときに色々なプログラム例はあったのですが、ほとんどがピクセル処理による描写で再現をしていて、タイリングをメッシュデータとして作れたらピクセルベースでは難しい用途にも使える可能性があるのではと考えたからです。このタイリングをベースに造形をするとか、いろいろ面白いことができそうです。そして何より、ゆくゆくは3Dに展開したいというのもあります。
今回の2Dの過程に関しては、基本的には Interactive Hyperbolic Tiling in the Poincare Discという記事に沿って再現してます。
パラメータ
まずは今回利用するパラメータを事前にNullノードなどを作って用意しておきます。今回利用するパラメータは全部で四種類です。
- p: 多角形の頂点の数
- q: 頂点に接する多角形の数
- rotate angle: 一番最初に作る多角形の回転角度
- iteration: 模様描写の拡張の回数

一個目の多角形をつくる


まず、ポワンカレディスクをHoudini上で表現するにあたって、半径1の円として表現することにします。
そしていきなりコーディングです。VEXを使って、ポワンカレディスク上に配置するタイリング模様の一個目の多角形を作るところから始めます。また話をシンプルにするために、一個目の多角形の中心はディスクの中心にくる前提にします。
まずパラメータとして条件を満たしたpとqの値を決定した上で、そのpとqの値に応じた多角形の半径を次のような計算式で算出します。
d = sqrt((tan(π / 2 - π / q) - tan(π / p)) / (tan(π / 2 - π / q) + tan(π / p)))
半径が出たら、原点を中心にしたその半径の大きさの円の上に、均等にpの数だけ点をプロットします(p=7だったら七角形になるように)。普通ならここでこのプロットした点を直線で結んで七角形としたいところですが、先に言った通り双曲幾何学空間では直線は曲線として表現されます。今回のポワンカレディスクでは円弧として表現されることになります。これを双曲線と言います。
ではこの双曲線をどう作ればいいかという点ですが、基本的にこの双曲線は円弧でるので、それを描写するための円弧の中心と角度、及び半径がわかればいいということになります。円弧の端点はすでに作っているので、実際に必要なのは円弧の中心点の位置と半径だけになります。この円弧の特徴の一つとして、この円弧のベースとなる円は先に作った多角形の隣り合う2つの頂点以外に、その2つの頂点を半径1の円(ポワンカレディスク)で反転させた2つの頂点も通るというものがあります。つまりすでに得られている2つの頂点に加えて、どれか一つの頂点を半径1の円で反転させた頂点を得られれば、3点から円の中心点と半径を得られることが可能となります。
では、反転といったとき双曲幾何学ではどのように行うのかということを考える必要があります。ユークリッド幾何学では直線を軸に反転することで見た目的には相似の図を得ることができます。HoudiniのMirrorノードにあたります。でもこの手法は双曲幾何学では使えません。双曲幾何学における直線はユークリッド幾何学における円弧(円)だからです。なので、円弧を利用した反転をする必要があるわけです。この変換をメビウス変換と言います。
このメビウス変換は別に反転だけのものに使うものではなく、移動や回転、拡張にも使うものですが、今回は反転に限って利用します。次のような計算式を利用することでユークリッド幾何学上で表現できる形で双曲幾何学の頂点を反転することができます。
その計算式はこのフォーラムにかかれている情報を参考にしました。
float a = r * r / (pow((p.x - o.x), 2) + pow((p.y - o.y), 2));
vector2 set(a * (p.x - o.x) + o.x, a * (p.y - o.y) + o.y);
これを利用することで、円を構成する3つの頂点が多角形の辺ごとに得ることができるようになります。あとはその円から2つの頂点の位置で円弧を取り出し描写するだけです。VEXでそのあたりはすべてやっているので、その具体的な方法はHIPファイルを確認してください。
再帰計算のための初期設定


タイリング模様はFor Eachノードを利用した再帰計算を行うことで拡張して作っていきます。そのための初期設定を行います。
拡張に利用するプリミティブ(曲線)をextendというグループに、最終的なメッシュとして利用するサーフェスをsurfaceというグループに入れています。
多角形タイリングの拡張(再帰計算中)


For Eachノードを利用して再帰計算が行えるようにします。Feedbackタイプにして前の計算結果を利用して次の図形を作れるようにしておきます。パラメータで設定したiterationを利用して、何回再帰計算を行うかも設定できるようにしておきます。回数が多ければ多いほど、多角形の数が増えます(そして計算量が増え重くなります)。
ここでこのプロジェクトの中で二番目に重要な拡張の部分、これもVEXで書きます。ここでは基本的には先に使ったメビウス変換による反転を今度は先に作ったそれぞれの円弧の中心点と半径を利用して図形を構成する頂点に対して行っています。ただ全ての頂点を反転させると無駄に重複して図形を生むことになるので、円弧の中心点を利用した反転は、その円弧が属している多角形に対してだけ行うという条件を付加しておきます。
サーフェス化する(再帰計算中)


反転操作によって追加された多角形からサーフェスを作ります。
重複しているサーフェスを削除(再帰計算中)


一応拡張しているときに重複をなるべく避けるような条件を入れているわけですが、それでもどうしても重複していくる面は出てくるわけです。このまま進めてもエラーにはならないのですが、計算量が指数関数的に重くなってしまうので、この段階で重複しているサーフェスや拡張に利用する曲線のプリミティブは削除しておきます。最適化しているわけですね。
完成
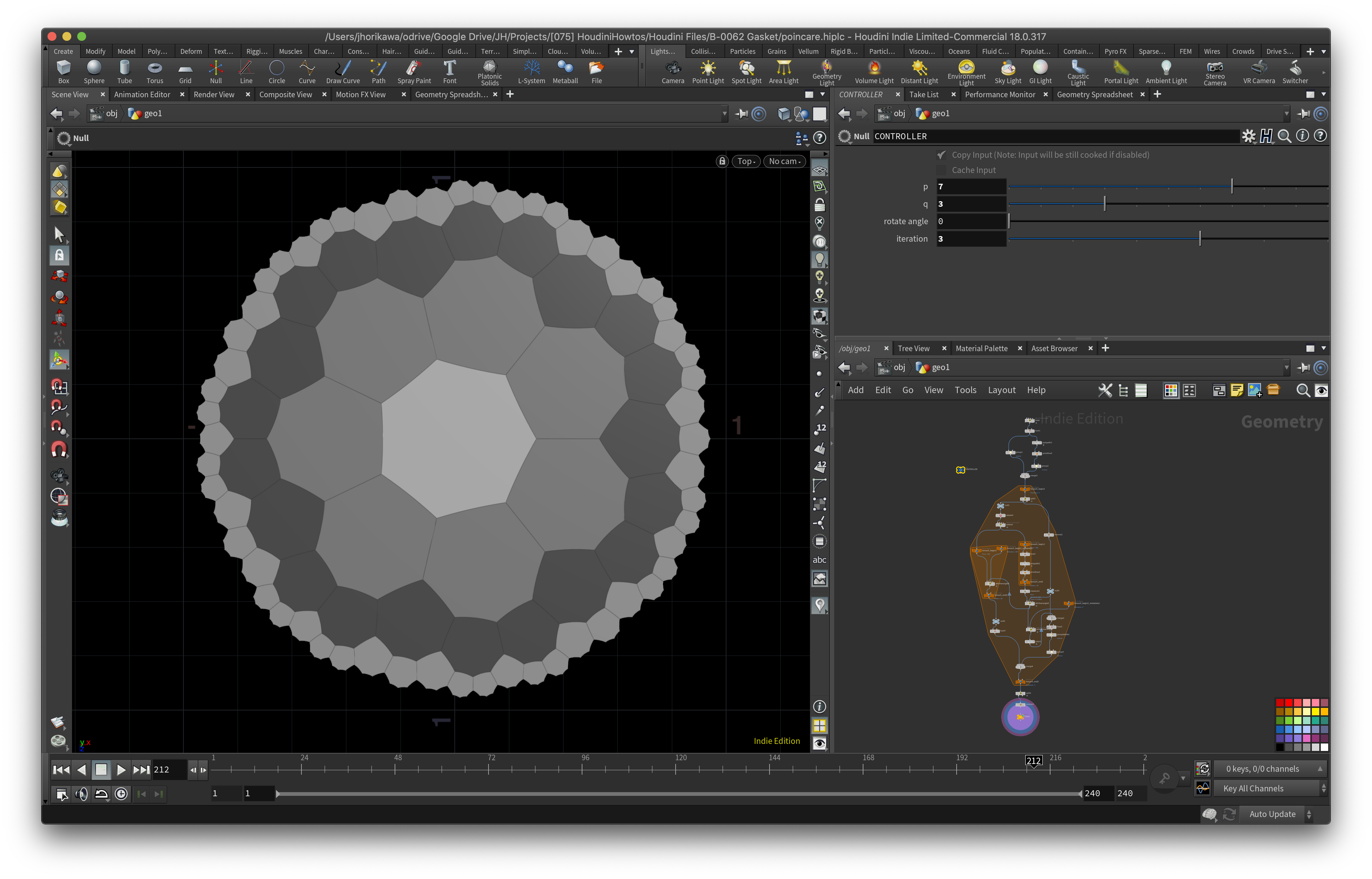
ループを抜ければ完成です。これまで拡張して作られた多角形が作られた順番に応じて色を変えてMergeされるようにしています。


バリエーション
パラメータを変えていくつかバリエーションを見てみましょう。こういう模様、大好きです。




まとめ
正直、まだやりたいことはたくさんあります。例えば、今回は最初の多角形の中心点はポアンカレディスクの中心に来ていますが、本当は中心点をずらすことも可能です。その場合、最初の多角形はユークリッド幾何学平面上は半径と角度が一定ではなくなるため、それもメビウス変換を利用する必要があります。この部分で散々悩んで、まだできていないので、可能であれば中心点も変えられるようにしていきたいなと考えています。
また、ぜひこれを読んだ方はチャレンジして頂いて、僕(@jhorikawa_err)にその方法を教えてくださいませ。。!
プロジェクトデータダウンロード先
Poincare Disk TilingのHIPファイルダウンロード先