本記事はHoudini Advent Calendar 2023の17日目の記事です。

HoudiniでSeifert Surfaces（ザイフェルト曲面）の可視化

はじめに

今回はHoudiniで面白い幾何学的なかたちをひとつ実装する方法を書いてみたいと思います。

テーマは「Seifert Surface（ザイフェルト曲面）」です。

ザイフェルト曲面は、幾何学のトポロジー分野において、結び目（ノット）の境界となる指向性を持つ曲面（後述）のことです。この結び目はロープが複雑に絡み合ったような形になっていて、その周囲を覆う形で形成される曲面をザイフェルト曲面と言います。このザイフェルト曲面をHoudiniで可視化してみましょう。

図1. ザイフェルト曲面

今回可視化にあたって、「Visualization of Seifert Surfaces _ JJ Van Wijk, AM Cohen」という論文を参照しています。その論文で説明されている手法を参考に（難しい計算式はすっとばして）、今回はパラメトリックに指定できるようにした結び目に対する曲面を、Houdiniというプラットフォームを使って作ってみようと思います。

ザイフェルト曲面の可視化のアルゴリズム

まずはざっとザイフェルト曲面の可視化のアルゴリズム（手順）を確認してみましょう。

1. 結び目（ノット）の選択
2. 結び目を編み込みとして表現する
3. 編み込みからザイフェルト曲面を生成

この手順を順番に詳しく説明していきたいと思います。

1. 結び目（ノット）の選択

ザイフェルト曲面は結び目の可視化とも言えるので、まずは結び目を選択する必要があります。

結び目とは、ひとつ、または複数の曲線が互いに絡み合って閉じたループを作ったものです。

結び目にはTrefoil knot（三葉結び目）などの有名なものもありますが、自分でカスタムな結び目を作ることも可能です。

名前が無い結び目に関しても自分で上記のような形でスケッチを書いてみるのも良いと思います。このとき、ひとつの曲線で結び目を作ってもいいですし、複数の曲線を使って作っても大丈夫です。

2. 結び目を編み込みとして表現する

結び目を選んだら、これを編み込みとして表現します。ここで言う編み込み表現とはどういうことかというと、曲線の経路や絡み合い方を編み込みとして構造的に記述するということです。

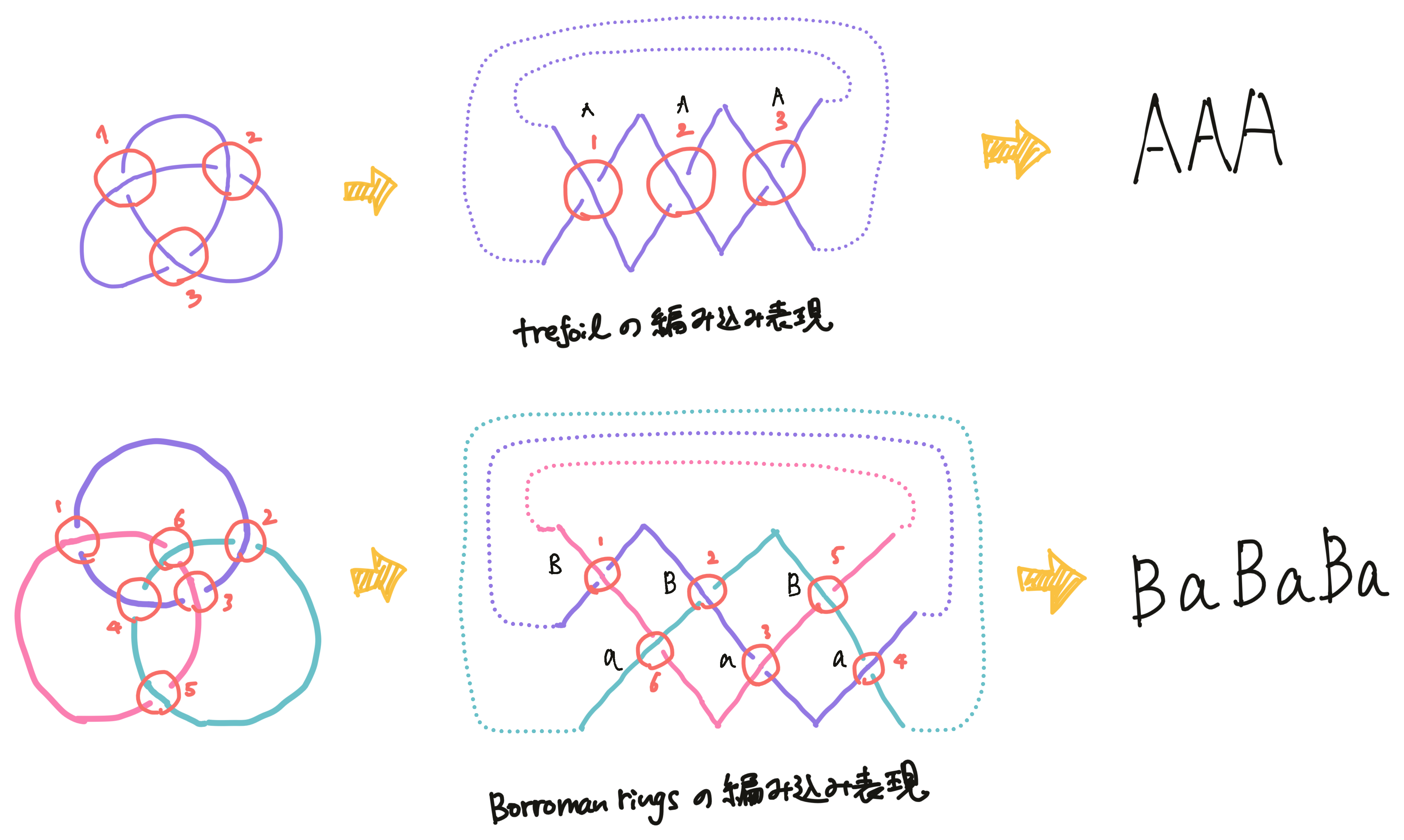
記述の方式は色々あるようですが、ここでは論文で説明されている方法で記述をしてみたいと思います。選んだ結び目の図に対して、編み込み表現として下記の図のように構造的に表現しなおします。

編み込み表現に変換するに当たり、次のようなルールに沿って行います。

• いくつのループがあるか数える。
• 自己ループ、あるいは異なるループ間の編み込みの位置を確認する。
• 編み込みの交差点部分をX図として組み合わせてフラットに表現する。
• フラット表現では左右端の同じ高さにある線は結ばれるものとする。
• フラットに表現したら、左から交差点をアルファベットで表現し直す。
• 交差点の高さに応じてアルファベットを決定する（一番下がA、次の段がBのように）。
• 交差点の部分で、左上から右下に向かう線が上に来る場合はアルファベットを大文字、左下から右上に向かう線が上に来る場合は小文字にする。
• 他に、アルファベットの直後に2などの数値が来たら、同じ曲線のペアでその位置で二回交差（巻いている）ことを示す。

3. 編み込みからザイフェルト曲面を生成

編み込み表現をアルファベットで記述できたら、いよいよHoudiniでの作業開始です。具体的に次のようなステップを踏んで形を作っていきます。

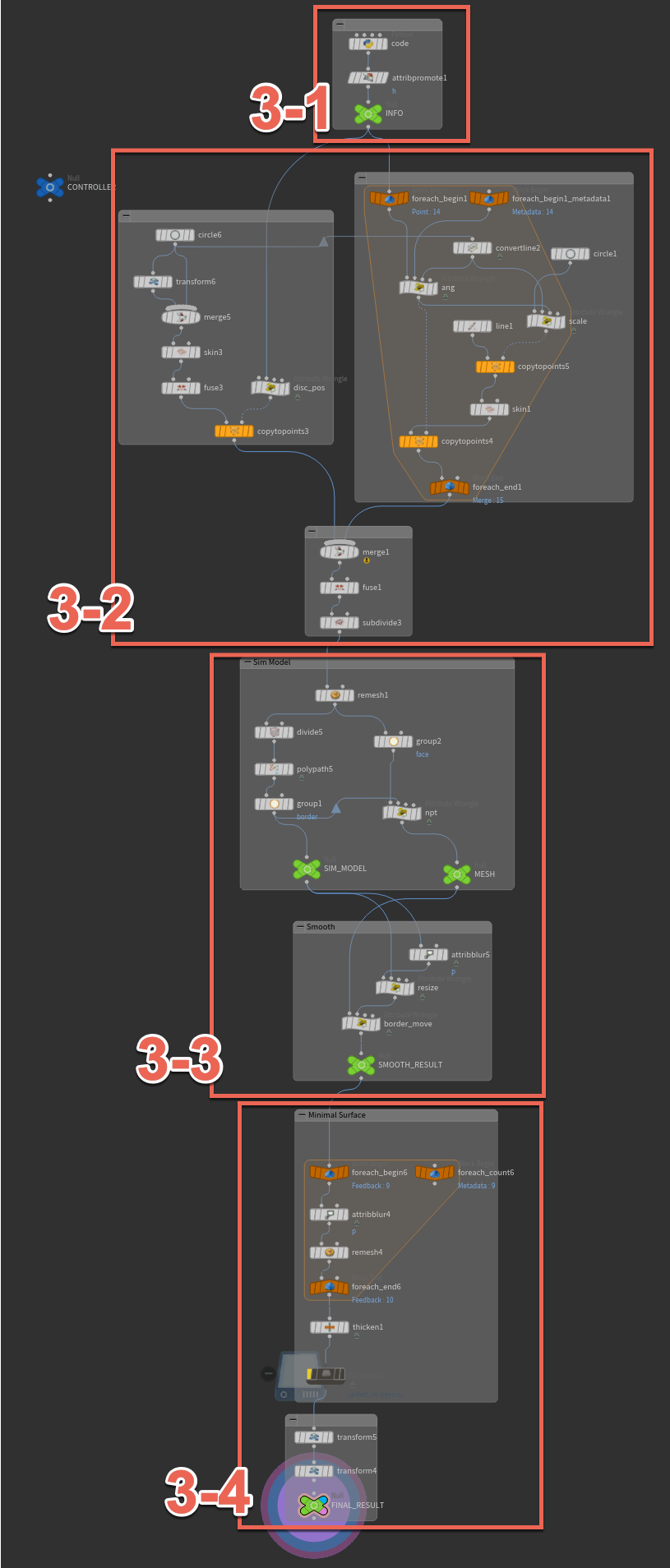
3-1. アルファベットコード（編み込み情報）のデコーディング
3-2. 編み込み情報を元にザイフェルト曲面のベースを作る
3-3. 曲面の境界線をスムージング
3-4. 境界線を固定して、ミニマルサーフェスを作る

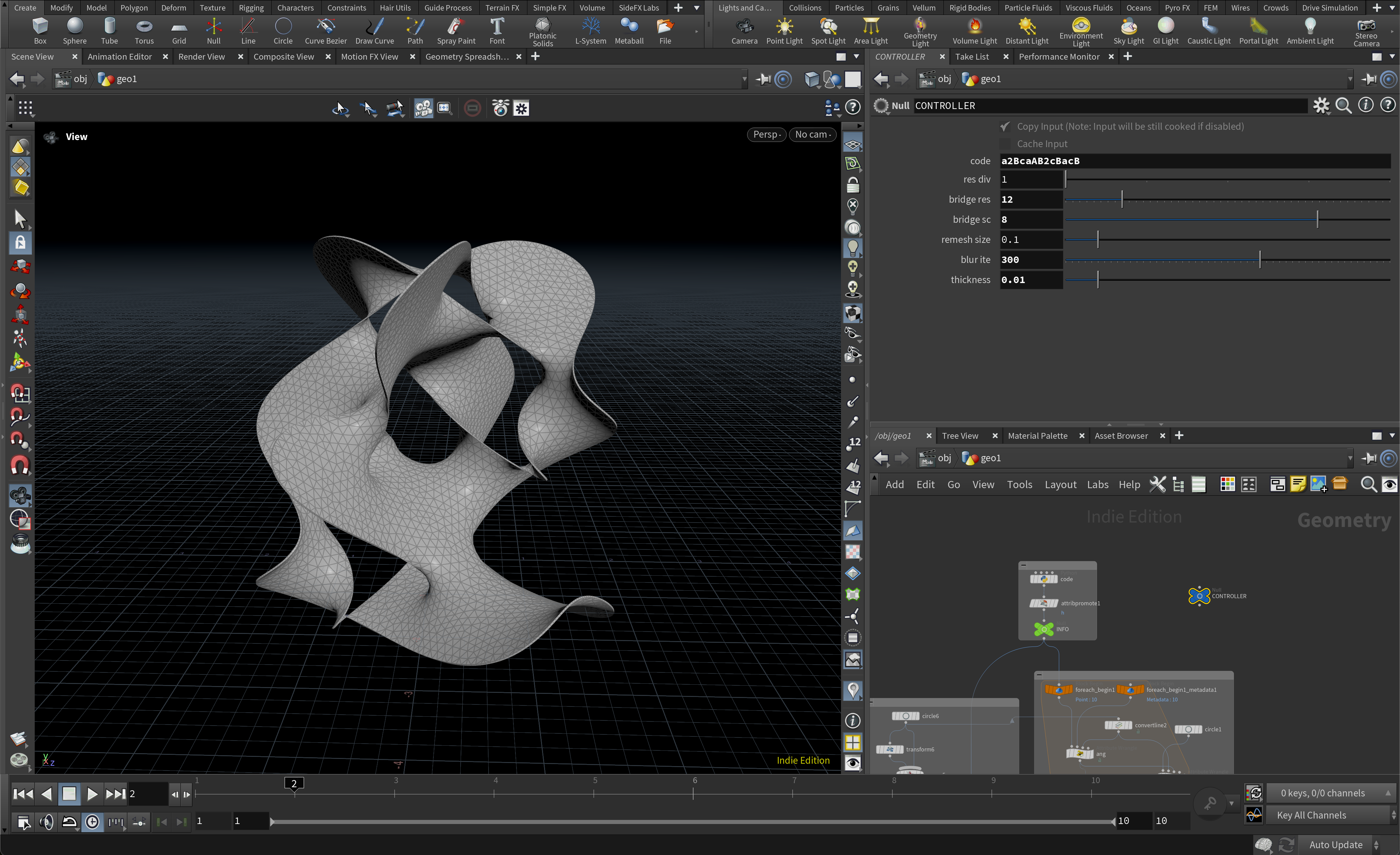
3-1. アルファベットコード（編み込み情報）のデコーディング

前述した編み込みの記述法により、編み込みはAAA（Trefoil）やBaBaBa（Borroman rings）のように表現されます。それをHoudiniで使いやすいように翻訳（デコード）したいと思います。

ここでは文字列に対する構文解析（パーシング）がしやすいPythonを利用します。基本的にやりたいことは、文字列として入力された編み込みコードを、アルファベット一個に対してポイントを一個つくり、そこに必要な情報をアトリビュートとして投げ込むということです。ポイントとして表現することで、後ほどVEX等で情報にアクセスしやすくなるからです。

ここでやりたいこととしては、

• アルファベットごとにポイントを作る
• アルファベットを整数に変換（A/a->0, B/b->1）、アトリビュートとしてポイントに格納
• アルファベットに続いて数値がある場合は、回転数のアトリビュートとしてポイントに格納
• アルファベットが大文字の場合、clockwiseというグループにポイントを入れる

これにより、必要な交点の数と、交点ごとの位置や回転の数と方向が決まります。

node = hou.pwd()
geo = node.geometry()

code = node.parm("code").eval()
alphabet = "ABCDEFGHIJKLMNOPQRSTUVWXZ"
group = geo.createPointGroup("clockwise")
geo.addAttrib(hou.attribType.Point, "h", 0)
geo.addAttrib(hou.attribType.Point, "t", 1)
lastpt = None
for i in range(len(code)):
    c = code[i]
    upper = c.isupper()
    
    uc = c.upper()
    n = alphabet.find(uc)
    
    if n < 0:
        if lastpt != None:
            try:
                tnum = int(c)
                lastpt.setAttribValue("t",tnum)
            except ValueError:
                print("val error")
            
    else:
        pt = geo.createPoint()
        lastpt = pt
        pt.setAttribValue("h", n)
        if(upper):
            group.add(pt)

3-2. 編み込み情報を元にザイフェルト曲面のベースを作る

このパートがHoudiniを使った、本編のメインとも言える部分です。

編み込み情報を曲面形状に変換するに当たって、論文を元に次のようなステップを踏んでザイフェルト曲面を作ります。

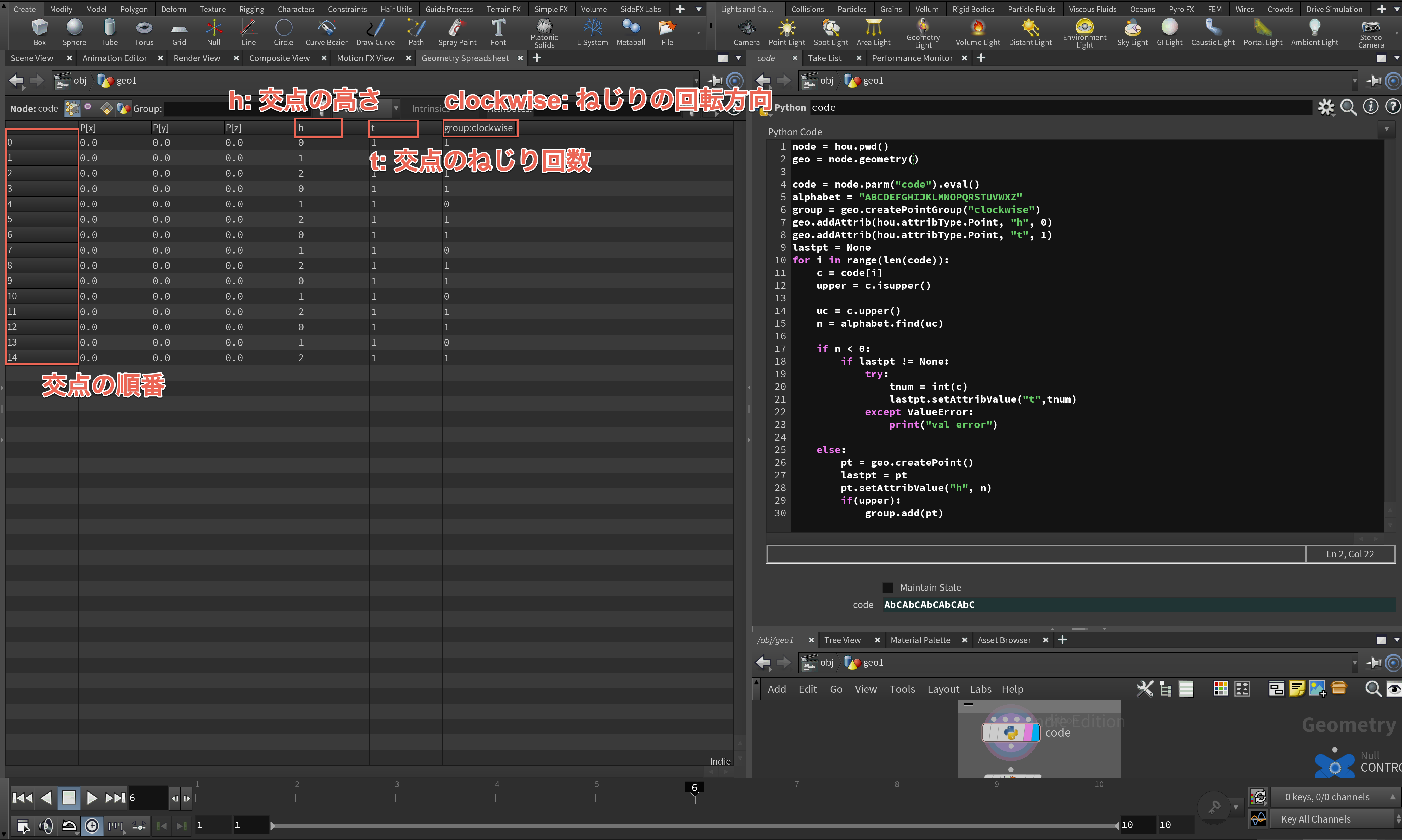
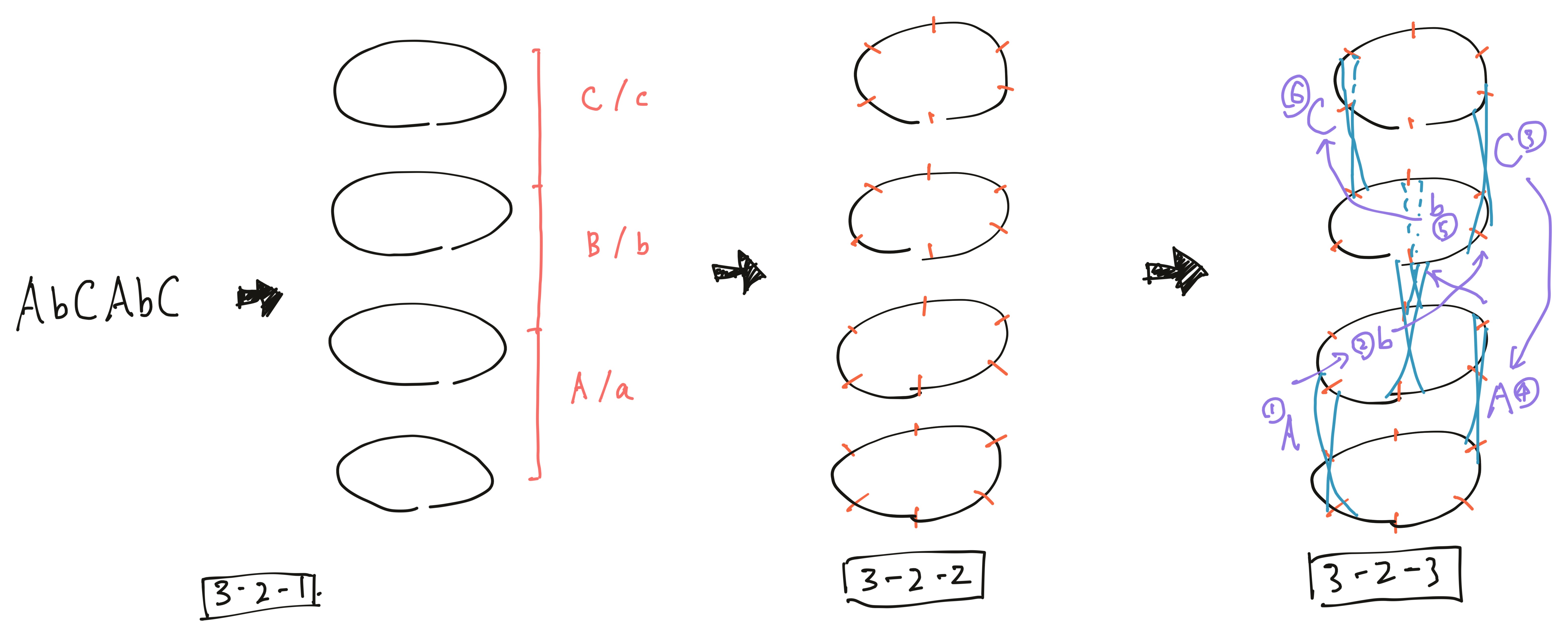
3-2-1. 交点の高さの種類の数に応じて円を積み上げるように配置する。
3-2-2. 交点の数だけ円を分割する。
3-2-3. 円の分割点に異なる高さにある円同士を結ぶブリッジを作る。

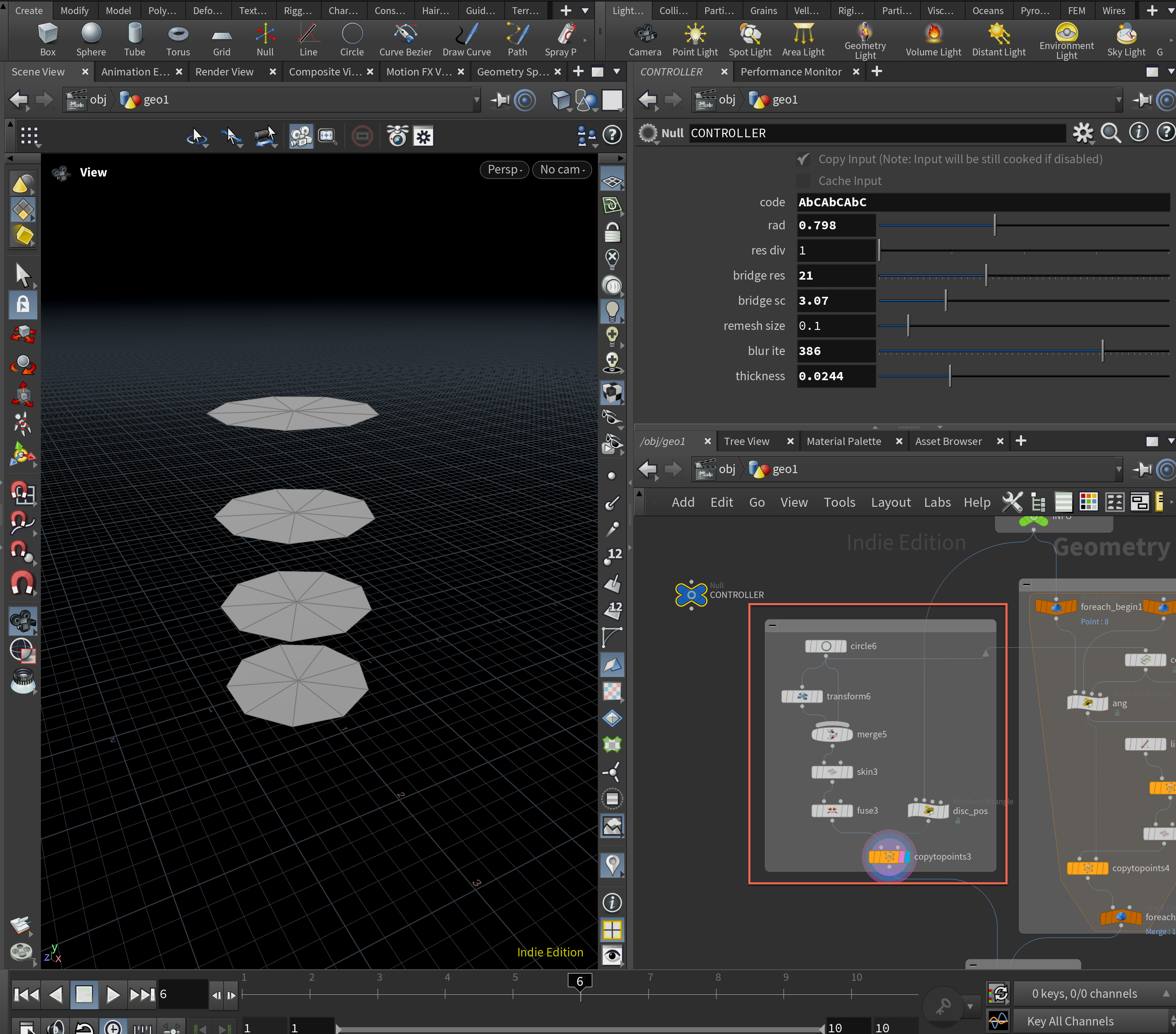
3-2-1. 交点の高さの種類の数に応じて円を積み上げるように配置する。

アルファベットで表現された交点の高さの種類に応じて、円を高さ方向に配置します。例えばAbCAbCAbCというコードがある場合は、AとBとCというキャラクターがあるので、全部で３つの交点があることがわかります。この交点は、三次元曲面においては２つの円を結ぶブリッジとして表現されることになります。このことから円の合計数は、交点の高さ種類の数+1となります。交点の高さ種類が3の場合は円の数は4となります。

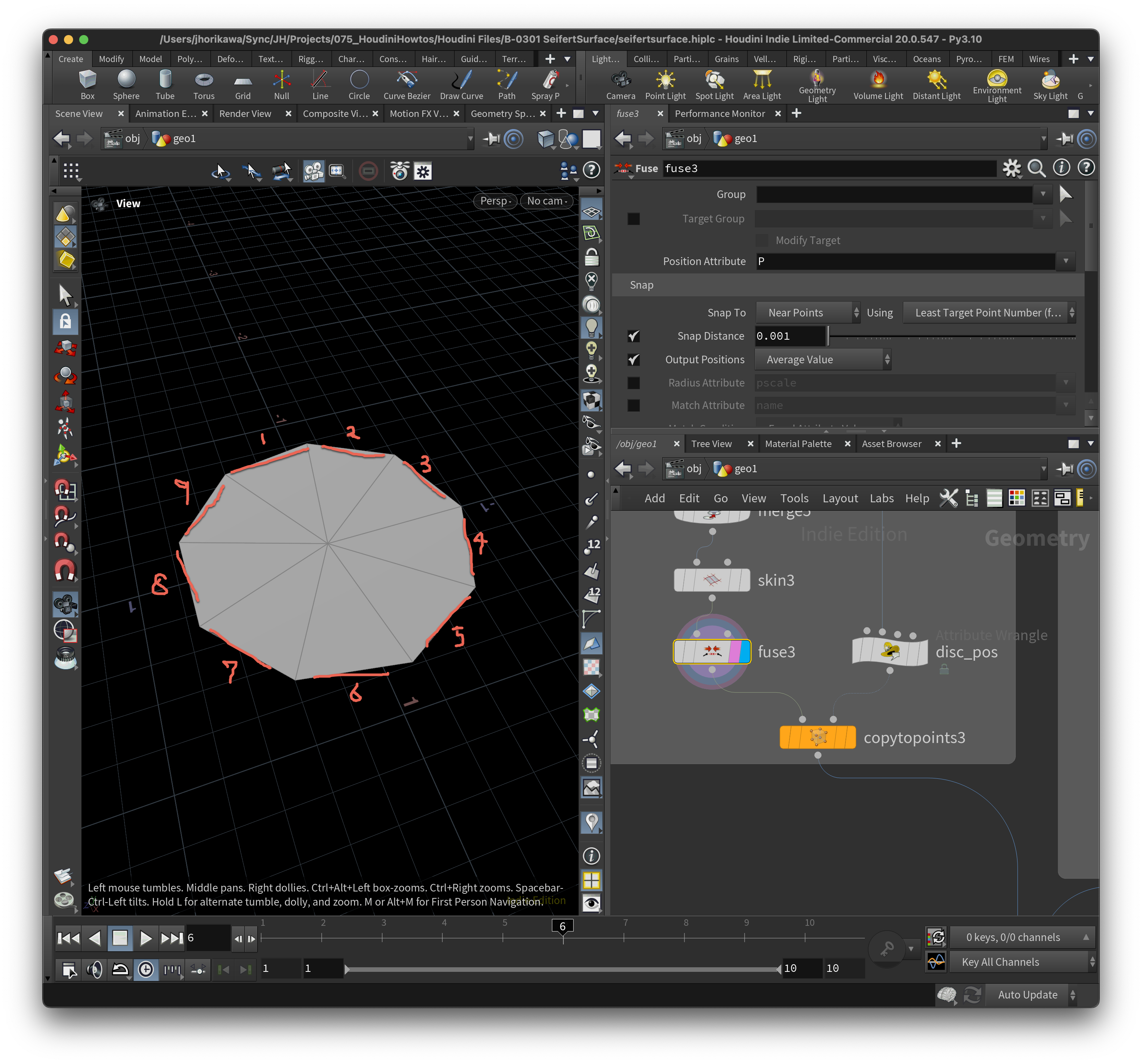
3-2-2. 交点の数だけ円を分割する。

高さ方向に配置する円の分割数は交点の数と同じ、あるいはその倍数にします。分割された円のエッジに異なる円同士をブリッジングするためです。

3-2-3. 円の分割点に異なる高さにある円同士を結ぶブリッジを作る。

円同士をブリッジングする際、リボン形状の橋を作ることになります。このとき注意したいのは、orientation（指向性）です。円の表裏方向と、円をつなげるブリッジの表裏方向はすべて揃っている必要があるということです。これが指向性があるということです。

• 指向性がない形状の例としてはメビウスの輪があります。メビウスの輪は面の表と裏面が途中切り替わる点があります。こういう形状は指向性が無いと言います。

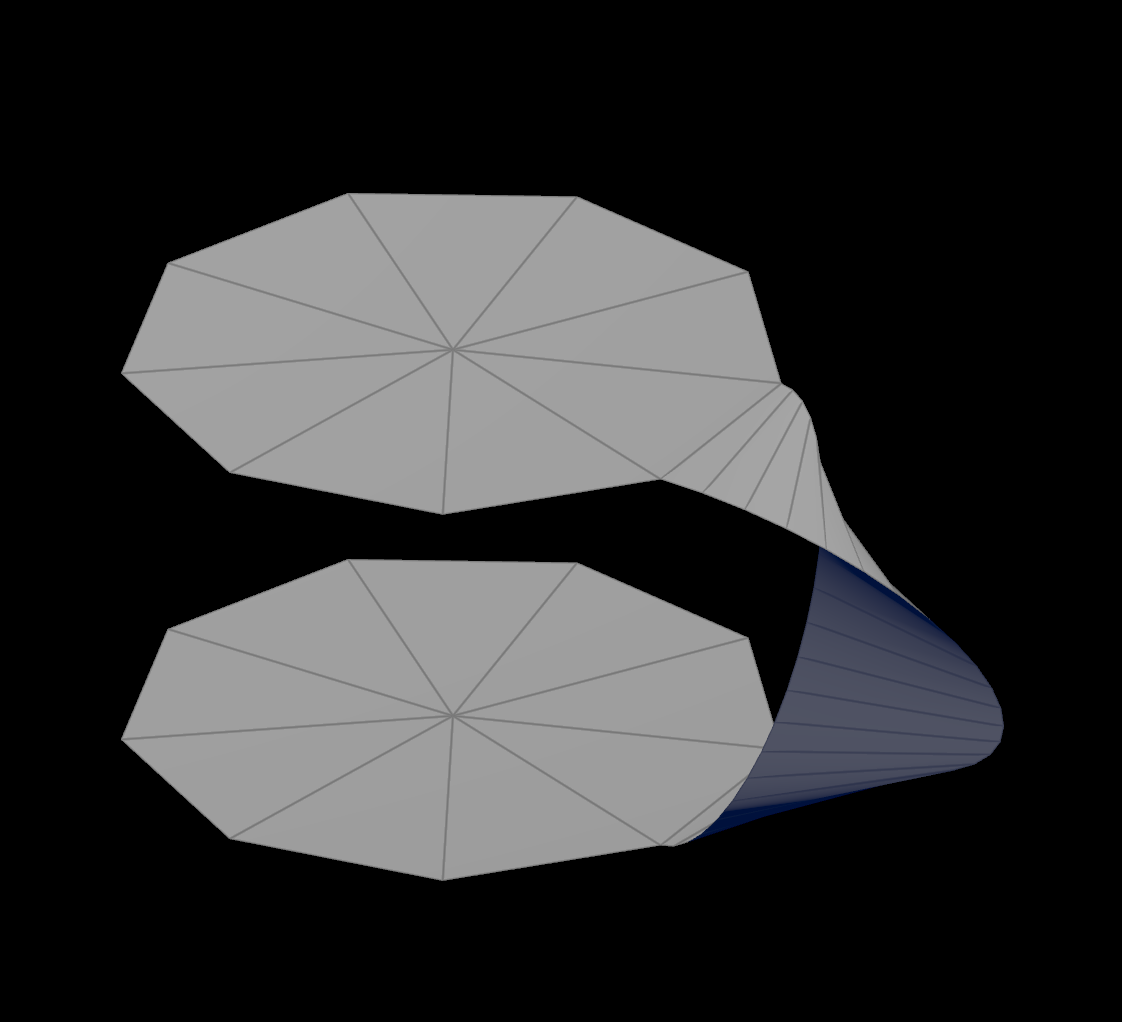
では、Houdini上で、すべてY+方向に表面が向いている円同士を、指向性を保ったまま結ぶには、どういう橋をかける必要があるでしょうか？単純にリボン形状をかけただけだとリボンの一方の端では円形と組み合わせた際指向性があっても、もう片方では指向性がないメビウスの輪と同じ状況になってしまいます。

そのため、ブリッジをかける際180度ねじることでリボンの両端が円と結合されても指向性を保てるようにします。

そして編み込みのコードでA2のようにアルファベットに続いて整数が来た場合は、ねじりの回数をそのかずに応じて増やします。nを数値としたとき、ねじりの角度は次のようになります。数値の表記がない場合、デフォルトでn=1とします。

t (twist angle) = n * π * 2 - π

また、編み込みコードからブリッジの高さを割り出します（Aであれば一番下の円とその上の円を結ぶブリッジといったように）。ブリッジのが配置されるのは円のエッジの部分になるので、円のエッジを反時計回りに順番にたどり、その平面位置、かつ先に割り出した高さの位置に最終的にブリッジを配置します。

3-3. 曲面の境界線をスムージング

さて、実は円にブリッジングをかけた形状自体、実はもうすでにザイフェルト曲面といえるのですが、ただあまり綺麗な形ではありません。そこで、形状のスタイリングをポスト処理として行って行きます。

まずは形状のボーダー（境界線）のスムージングを行います。ここではあえて曲面自体のスムージングは考えず、あくまで境界線だけを考えます。曲面自体は次のステップで行います。

具体的にはまずはボーダーを曲面から取り出します。

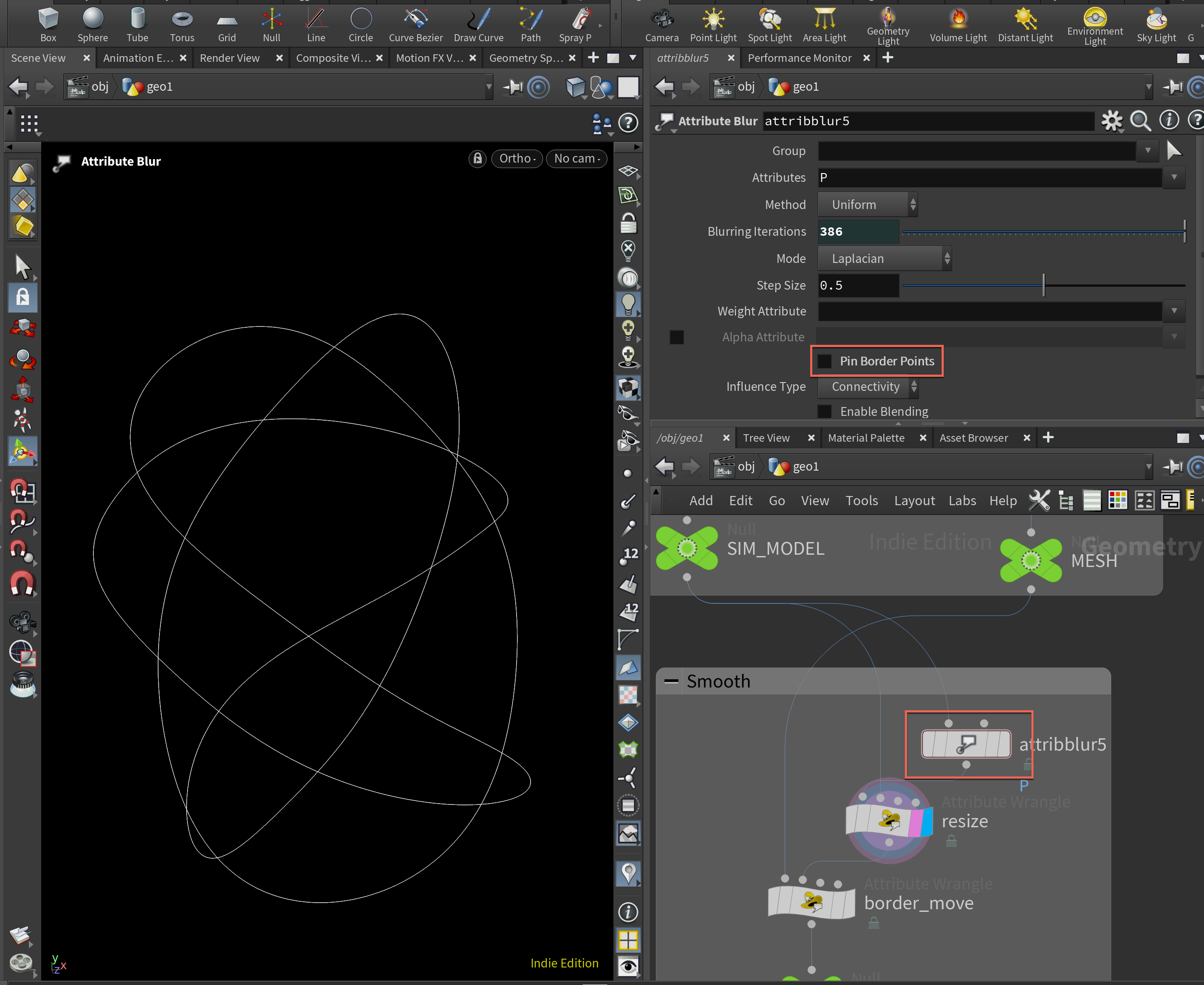
そしてその境界曲線をAttribute Blurなどでスムージングします。このときスムージングのiteration数はパラメトリックにしておくと最終的にほしい形状のコントロールができるようになります。

スムージングがてきたら、元もメッシュの境界線部分だけスムージングされた曲線に合わせて変形します。この時点では内側の曲面時点はとても汚いことになっていますが、それを次のステップで修正します。

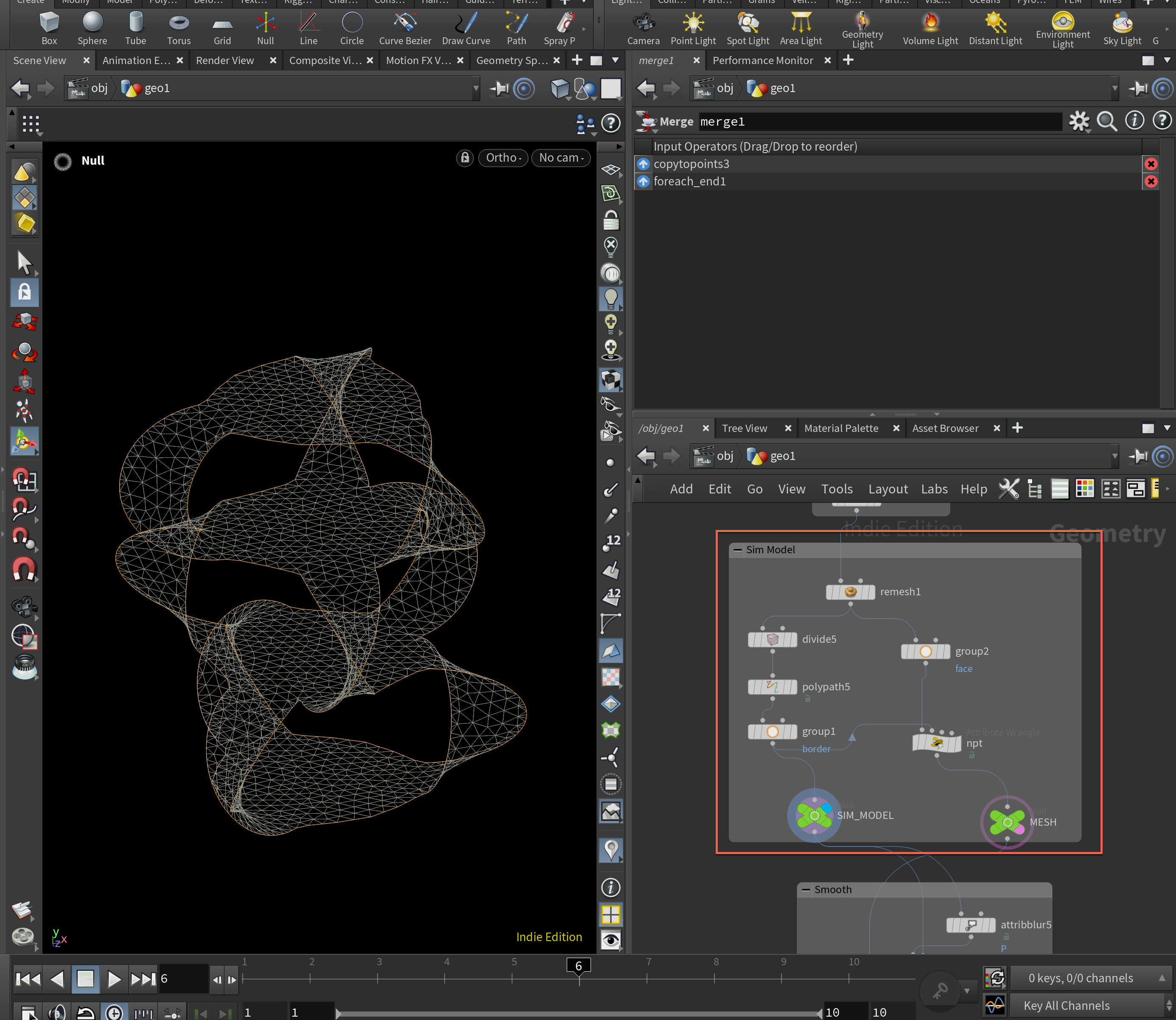
3-4. 境界線を固定して、ミニマルサーフェスを作る

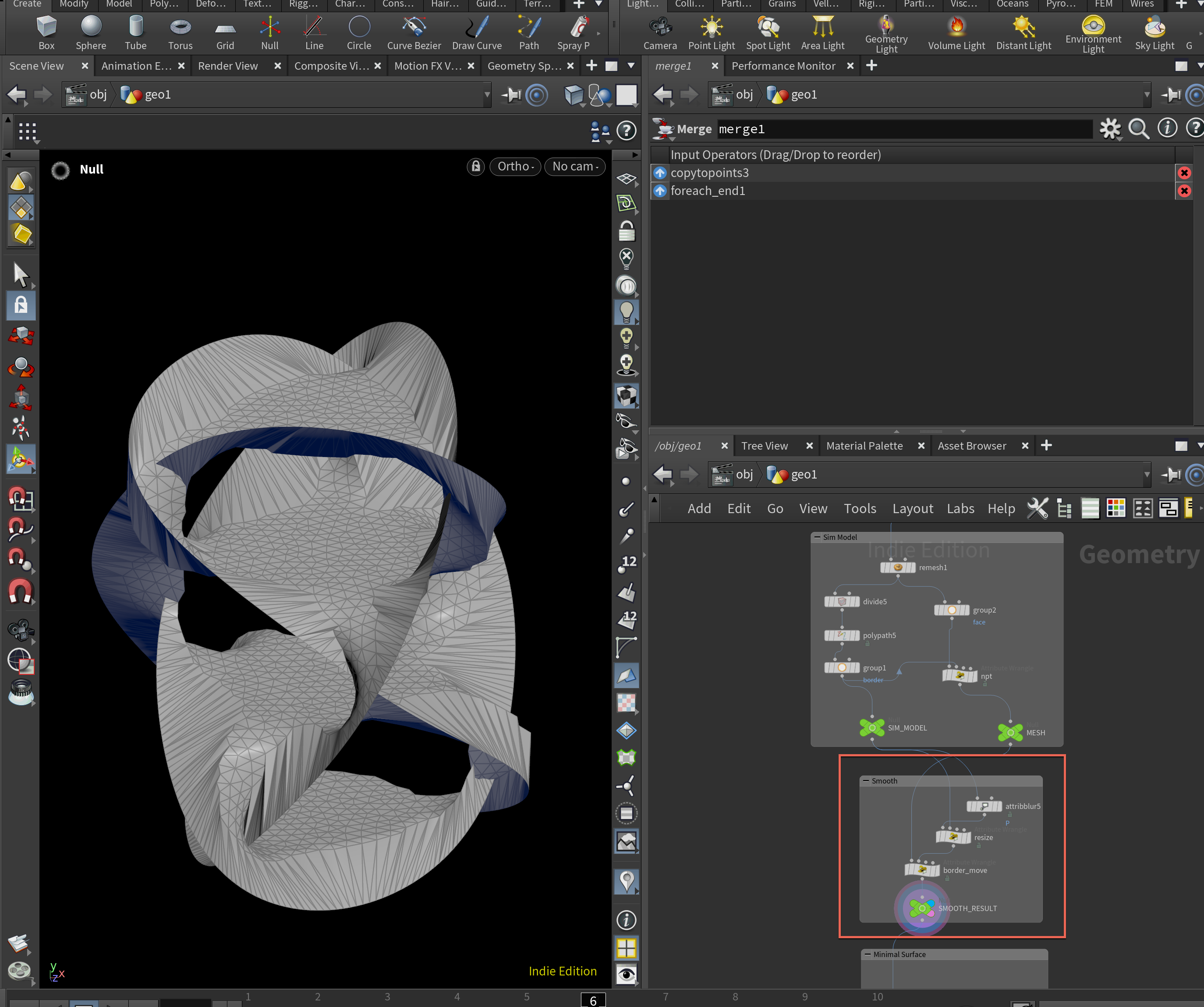
最後のステップでは、スムージングされた境界線部分を固定し、内側の曲面だけスムージングを行います。ここではAttribute blurノードをRemeshと組み合わせて再帰的に処理を施しています。この処理を行うことで、ミニマルサーフェス（面積が最小になるような曲面）を得ることができます。

結果

得られた結果は今回Karmaで簡易にレンダリングしてみました（Karma初心者です）。いくつかレンダリング画像を載せます。

まとめ

今回はザイフェルト曲面の可視化に特化して説明しましたが、ザイフェルト曲面自体面白い特徴を色々持っているので、詳しくはSeifert Surface on Wikipediaなどを参照してください。私がこの曲面についてどこで知ったのか忘れましたが（多分Youtubeライブ配信中のコメント）、こういった面白い幾何学に関して他にもなにか知っている方がいらっしゃったらぜひ教えてください。

それでは良いお年を。

プロジェクトファイル