はじめに
今回もかなり需要が限られる話かもしれませんが、
巷で話題のAIにまつわる論文のなかでなかなか興味深いものがありましたので
それについて書こうと思います
画像生成が話題ですが、自分のなかではMDM(Human Motion Diffusion Model) の関連論文が興味深かったのですが、
そこで "6D回転" という概念を知ります
MDMと6D回転ってなんだ?
MDMとはテキストから3次元空間のボーン・メッシュの変形を推定するなどモーション生成AIの研究論文です
MDMでは2Dto3Dの姿勢推定AIの別論文の研究内容が利用されています
それが6D回転です
6D回転は2次元の画像に書かれている人間の顔の姿勢を、
3次元姿勢に推定するAiModelに関する研究論文で扱われている回転行列のデータタイプです
6D回転は従来の従来手法の実行パフォーマンスに比べて20%以上効率をアップさせることが可能になると述べられています
論文
6D ROTATION REPRESENTATION FOR UNCONSTRAINED HEAD POSE ESTIMATION
これはなにかに使えないか?
マトリクスのミラーリング検証中は実行時の処理速度等を比べたことはありませんでした
しかし、6D回転のほうが20%パフォーマンスが早いのなら6D回転のミラーを実装すると
多くの骨を持つキャラのトランスフォーム処理も早くなったりするのか?と試したくなりました
(専門用語も多い論文の解読は挫折して分かる部分だけしか読めてません・・・)
しかしまずは6D回転検証の前に6D回転そのものについていろいろと書きたいと思います
(自分でも色々忘れそうなので記録する意味も大きいです)
姿勢推定に6D回転をなぜ使うか
6D回転の論文内では回転計算によく登場するデータタイプについて、要約するとこう書かれています
「オイラー回転や4次元以上の回転の表現が不連続であり、ニューラルネットワークの学習には理想的でない」
オイラー回転はご存知の方も多いかと思いますが、ジンバルロックというバグをかかえます
またクォータニオンも姿勢が不明になるタイミングがあります
なぜ姿勢の推定が不明になるか考察する
クォータニオンは共益複素数の概念が扱われます
詳しくは参考資料紹介の部分を見ていただくとして
共益複素数は、複素数の虚部の符号を反転させた複素数のことです
共益クォータニオンとはそのまま、クォータニオンの逆回転を意味します
ではここで、クォータニオンの回転を回転行列として改めて考えると
XY平面、YZ平面、XZ平面でそれぞれのベクトルを回転させていることになりますが、
角度で表せるということは以下がなりたってしまいます
- 360度は復元できない(0度である)
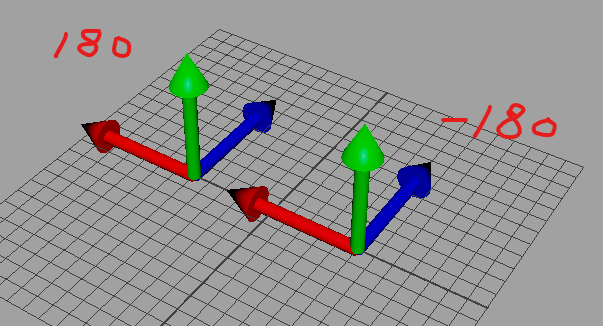
- n度と-n度は復元できない
- 回転順がないので、同じ方向にむいていてもXYZ軸の回転量に再現性がない
回転値は違うはずなのに、姿勢が一致してしまいました
クオータニオンは回転行列と同じ扱いですが回転順序がありません
同じ回転行列を渡しても厳密には回転する際にXYZの軸回転量が入れ替わったりします
心当たりがある方もいるかも知れません、
Unityは回転にクォータニオンが利用されていますが、
Mayaで360度以上の角度をつけて配置していてもUnity内の回転値が一致しない
といった具合です
3はクオータニオンの成分そのものはベクトルの座標ですから、
オイラーなどでは連続するような角度も、クォータニオンではどの軸がどれくらい回転したのか判断不能になってしまい連続性が失われます
これはおかしいなことになりそうですね?
回転行列は回転順序をもっており、
順番に軸回転できるので、元の姿勢と数値的な一致が保証されるようです
このことが拡散モデルに使われるニューラルネットワークの学習にとっては都合が悪いのではないかと思います
さて、クォータニオンが扱えないので6D回転を使うということですが、
6D回転はどういう要素をもっているのでしょうか?
6Dの要素
6D回転は直行交差する2つのベクトル同士の外積から、3次元空間の回転行列に必要なもう1軸ベクトルが割り出せる性質を利用して、回転行列の2軸のベクトルのみを圧縮格納したものです
つまりシンプルにデータ量を抑えた優れものということで、
回転行列を表す概念であること自体は3x3の回転行列とあまり違いはありまあせん
6D = [Xx, Xy, Xz, Yx, Yy, Yz]となります
6D回転を使うと処理速度も早くなるか?
マトリクスの軸回転、クォータニオンのベクトル反転, 6D回転反転
それぞれにテストケースを試し処理速度の差を確認します
そこで6D回転を使うメリットがあるかを確認します
テストケース
1. 24個のトランスフォームに対してミラーする
1. 150個のトランスフォーム対してミラーする
とりあえず少ない数と多い数で差がでるか見ましょう
検証環境
Maya 2024.2
マトリクスの軸回転
マトリクスの軸回転では、こちらやcymelのミラー実装を参考に、以下の手法でYZ平面ミラーリングを行います
M_x=
\begin{bmatrix}
X_x,-X_y,-X_z\\
-Y_x,Y_y,Y_z\\
-Z_x,Z_y,Z_z\\
\end{bmatrix}
クォータニオンの軸回転
以下の手法でYZ平面ミラーリングを行います
Q_x =
\begin{pmatrix}
q_x, -q_y, -q_z, w
\end{pmatrix}
6D回転の軸回転
6Dは2軸しか要素がありませんので、
Up軸(Y)とSide軸(X)がわかっているとしてXベクトル方向に反転します
そこからZベクトルを外積で算出し回転行列に変換します
\begin{array}\
\vec Z=
\begin{pmatrix}
(-X_yY_z)-(-X_zY_y)\\
(X_z-Y_x)-X_xY_z\\
X_xY_y-(X_y-Y_x)
\end{pmatrix}\\
M_x=
\begin{bmatrix}
X_x,-X_y,-X_z\\
-Y_x,Y_y,Y_z\\
Z_x,Z_y,Z_z\\
\end{bmatrix}
\end{array}
検証コード
長いため折りたたみ
import time
import maya.api.OpenMaya as om2
import maya.cmds as cmds
def testMat(sellist: om2.MSelectionList, length):
# 時間計測開始
start = time.perf_counter()
for i in range(length):
dag_path = sellist.getDagPath(i)
m_matrix = dag_path.inclusiveMatrix()
m_matrix[1] = -m_matrix[1]
m_matrix[2] = -m_matrix[2]
m_matrix[4] = -m_matrix[4]
m_matrix[8] = -m_matrix[8]
cmds.xform(dag_path.fullPathName(), m=m_matrix, ws=True)
# 時間計測終了
end = time.perf_counter()
# 経過時間(秒)
progress = end - start
return progress
def testQuat(sellist: om2.MSelectionList, length):
# 時間計測開始
start = time.perf_counter()
_mq = om2.MQuaternion
for i in range(length):
dag_path = sellist.getDagPath(i)
m_matrix = dag_path.inclusiveMatrix()
m_quat = _mq().setValue(m_matrix.homogenize())
m_quat.y = -m_quat.y
m_quat.z = -m_quat.z
fix_4x4_matrix = m_quat.asMatrix()
fix_4x4_matrix[12] = m_matrix[12]
fix_4x4_matrix[13] = m_matrix[13]
fix_4x4_matrix[14] = m_matrix[14]
fix_4x4_matrix[15] = m_matrix[15]
cmds.xform(dag_path.fullPathName(), m=fix_4x4_matrix, ws=True)
# 時間計測終了
end = time.perf_counter()
# 経過時間(秒)
progress = end - start
return progress
def test6D(sellist: om2.MSelectionList, length):
def _rot6d_to_rotmat(m):
x = [m[0], m[1], m[2]]
y = [m[3], m[4], m[5]]
z = [
(m[1] * m[5]) - (m[2] * m[4]),
(m[2] * m[3]) - (m[0] * m[5]),
(m[0] * m[4]) - (m[1] * m[3]),
]
return [x, y, z]
# 時間計測開始
start = time.perf_counter()
for i in range(length):
dag_path = sellist.getDagPath(i)
m_matrix = dag_path.inclusiveMatrix()
# XY軸を反転
m_6d_matrix = [
m_matrix[0],
-m_matrix[1],
-m_matrix[2],
-m_matrix[4],
m_matrix[5],
m_matrix[6],
]
m_6d_matrix = _rot6d_to_rotmat(m_6d_matrix)
fix_4x4_matrix = [
m_6d_matrix[0][0],
m_6d_matrix[0][1],
m_6d_matrix[0][2],
0.0,
m_6d_matrix[1][0],
m_6d_matrix[1][1],
m_6d_matrix[1][2],
0.0,
m_6d_matrix[2][0],
m_6d_matrix[2][1],
m_6d_matrix[2][2],
0.0,
m_matrix[12],
m_matrix[13],
m_matrix[14],
m_matrix[15],
]
cmds.xform(dag_path.fullPathName(), m=fix_4x4_matrix, ws=True)
# 時間計測終了
end = time.perf_counter()
# 経過時間(秒)
progress = end - start
return progress
def getBestScore(sellist: om2.MSelectionList, length, func, count=100):
# ミラーを実行テスト
progress = 0
best_score = 10000000
for i in range(count):
result = func(sellist, length)
progress += result
if result == 0:
continue
if best_score > result:
best_score = result
# 平均時間を算出
progress_average = progress / count
return progress_average, best_score
def processSpeedTest():
# テスト対象のノードを取得
sellist = om2.MGlobal.getActiveSelectionList()
length = sellist.length()
# マトリクス軸ミラーを実行テスト
progress_average, best_score = getBestScore(sellist, length, testMat)
print(
f"matrix mirror: bone count [{length}] -> "
f"average {progress_average} sec, best score {best_score} sec"
)
progress_average, best_score = getBestScore(sellist, length, testQuat)
print(
f"quat mirror: bone count [{length}] -> "
f"average {progress_average} sec, best score {best_score} sec"
)
progress_average, best_score = getBestScore(sellist, length, test6D)
print(
f"6d rotate mirror: bone count [{length}] -> "
f"average {progress_average} sec, best score {best_score} sec"
)
計測結果
100回繰り返した平均速度とベストスコアを算出します
24
matrix mirror: bone count [24] -> average 0.0020757979922927917 sec, best score 0.0017932001501321793 sec
quat mirror: bone count [24] -> average 0.0020363599876873197 sec, best score 0.0018945999909192324 sec
6d rotate mirror: bone count [24] -> average 0.0019537920132279398 sec, best score 0.0018543999176472425 sec
150
matrix mirror: bone count [150] -> average 0.010847064002882689 sec, best score 0.010036699939519167 sec
quat mirror: bone count [150] -> average 0.011524874011520296 sec, best score 0.010705499909818172 sec
6d rotate mirror: bone count [150] -> average 0.011975099011324345 sec, best score 0.010916899889707565 sec
結論
どれつかっても速度は誤差でした
各所から「クォータニオンだけ関数つかってねぇで計算しろ」って
聞こえてきそうでですがこれでよしとしましょう
どうパフォーマンスとして優れているのだろう?
検証の結果からも論文が指すパフォーマンスはどちらかというとデータ転送速度などのパフォーマンスに思えます
外積計算をおこなったとしても、マトリクスの値のをいじるのと誤差なれば、
処理時間の違いがないのでメモリ量が単純におさえられるのは大きなメリットに思えます
AI系は計算をGPUでやることで処理が高速化されているので、
コンピュートシェーダーでなにか大量のマトリクスの処理を行うなどの場合に有効だったりするんでしょうか?
参考資料