検索・ソート(並び替え)
現代のインターネットは膨大なデータからデータを検索、並び替えることが多い(Google 検索など)
→ではどうやってそれを行っているのか??
↓視聴した動画
1. 基本的な処理数の表記方法
・O(): オーダ表記:処理回数の最大値を表す
・Ω(): オメガ表記:処理回数の最小回数を表す
・θ(): シータ表記:最大回数と最小回数が等しい場合に使用
→処理の実行速度を議論する場合は、O()最大値で考えることが多い
2.検索方法の例
2-1. 線形検索: linear search
1方向に対してデータを1つずつ確認して、検索する
データ数がnの場合、最大値O(n)・最小値Ω(1)となる
2-2. 二分探索: binary search
データがソートされていることを前提として、データを半分に分ける
→検索したいデータに近い方のデータをまた半分に分ける、同様の操作を繰り返す
→最終的に1つまたは見つからなくなるまで実施する
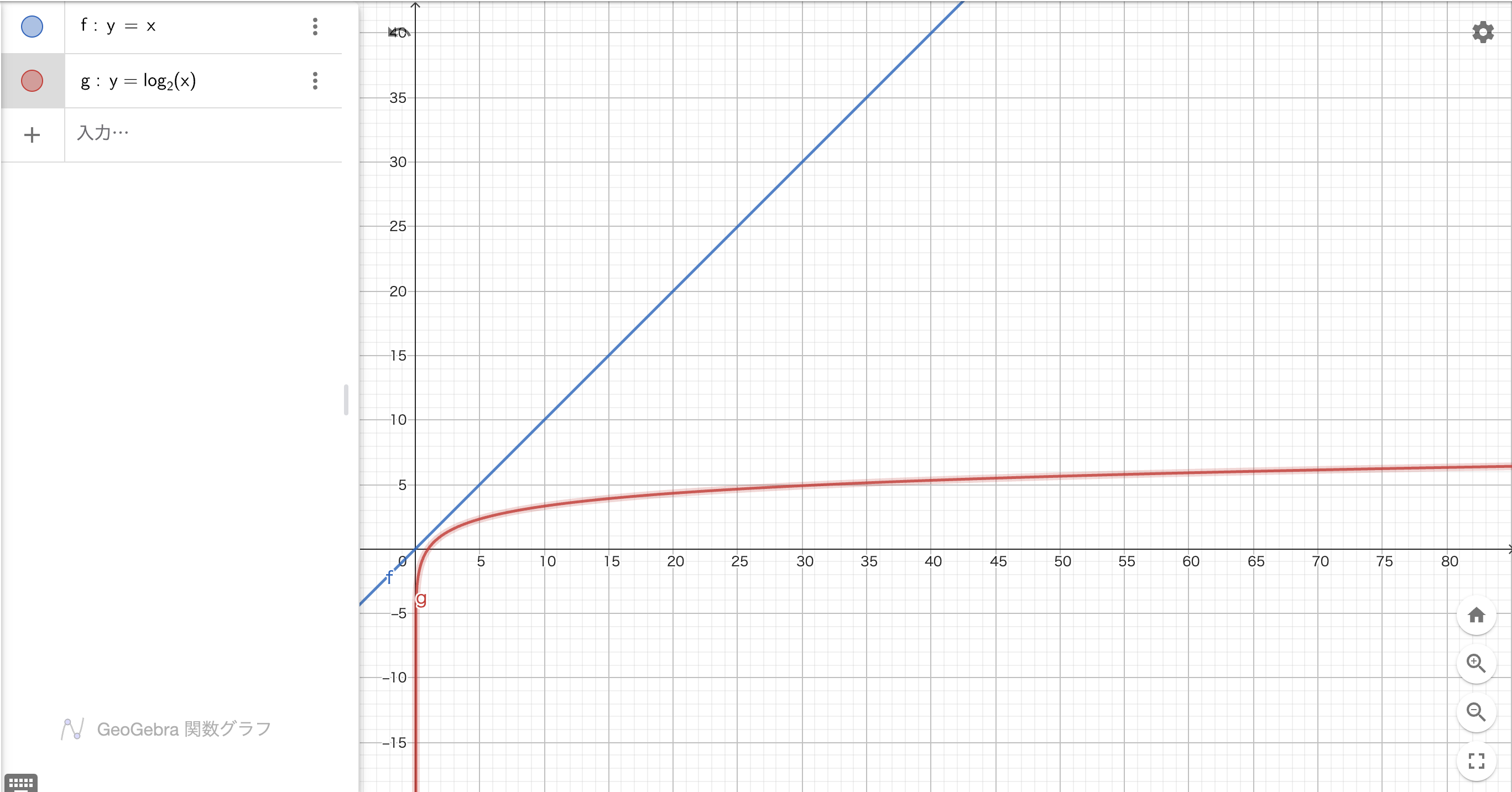
データ数がnの場合、最大値O(log n)・最小値Ω(1)
青線: 線形探索
赤線: 二分探索
x軸: データ数
y軸: 処理の回数
グラフを見ると圧倒的に二分探索の方が処理回数が少ないことがわかる
3. ソート(並び替え)
ランダムなデータの順番を一定の規則に基づき、並び替える処理のこと。
今回は数字を左から昇順にすることを想定
3-1. 選択ソート(select sort)
データを1つずつ見ていって、見つけた最小値を順番に入れ替える→繰り返す
ex)7 3 6 1 5 4 2 0 のデータを並び替える
step 1: 左から順に最小値を見ていく (7 3 6 1 5 4 2 0)
step 2: 0と一番左のデータを入れ替える ( 0 3 6 1 5 4 2 7)
step 3: step1, 2を繰り返す
(0 3 6 1 5 4 2 7)→(0 1 6 3 5 4 2 7)→(0 1 2 3 5 4 6 7)→(0 1 2 3 4 5 6 7)
実行回数
データ数がnの場合の実行回数の最大値はどうなるだろう??
1回目はn個のデータを確認する→並び替える→2回目はn-1個のデータを確認する→並び替える、、、、
= n + n - 1 + n - 2 + ,,,,,+ 1
= n(n + 1)/2
=n^2 + 2n
n→∞の場合、注目すべき項はn^2だけだ。つまり 最大値O(n^2) となる。
次に最小値を考える。最高の状態はすでにソートされている場合だ。
→最初からソートされているかはどうやって確認する?
→あれ、結局全部見ないとわからない?
→はい、結局全て確認しなければならない、、、、→ 最小値Ω(n^2)
⚪︎選択ソートのコード例
#include <cs50.h>
#include <stdio.h>
int main(void){
int array[] = {5, 2, 7, 4, 1, 6, 3, 0}; // 並び替えたい数字の配列
int arraylen = sizeof(array) / sizeof(array[0]); // 配列の要素数を取得
for (int j = 0; j < arraylen; j++){
int minIndex = j; // 最小値の要素番号を初期化
for(int i = j + 1; i < arraylen; i++){
if (array[i] <= array[minIndex]){
minIndex = i; // 最小値の要素番号を保存
}
}
int tmp = array[j]; // 最小値と入れ替える数字の保存
array[j] = array[minIndex]; // 最小値を入れ替える
array[minIndex] = tmp; // 最小値があった場所に入れ替え前の数字を入れる
}
for (int k = 0; k < arraylen; k++){ // ソート結果出力
printf("%i", array[k]);
}
printf("\n");
}
3-2. バブルソート(bubble sort)
隣り合うデータを比較して、大小関係が正しいか確認する。異なっていた場合は入れ替える→これを繰り返す
ex)3 0 6 1 5 4 7 2 のデータを並び替える
step 1: 3と0の大小関係を比較 (3 0 6 1 5 4 7 2)
step 2: 異なっているので、入れ替える( 0 3 6 1 5 4 7 2)
step 3: 3と6の大小関係を比較 (0 3 6 1 5 4 7 2)
step 4: 正しいので入れ替えず、次のデータを比較(0 3 6 1 5 4 7 2)
→この操作を繰り返す
(0 3 6 1 5 4 7 2)→(0 3 1 6 5 4 7 2)→(0 3 1 5 6 4 7 2)→(0 3 1 5 4 6 7 2)→(0 3 1 5 4 6 7 2)→,,,,,(0 1 2 3 4 5 6 7)
実行回数
今回もデータ数が n の場合の最大数を考える
・データを1周した時に隣同士のデータを比較する回数は、、、、n-1 回
・もし、一番小さい数が右端にあった場合、データを何周すると左端に来るだろうか?、、、、、n-1 周
つまり、実行回数は
=(n-1)*(n-1)
=n^2 - 2n + 1
n→∞の場合考慮すべき項はn^2→したがって 最大値O(n^2) となる
次に最小値を考える。ここでも同様にソートする際の最高の初期状態はすでにソートされている場合だ
⇨ソートされていても1周は確認する必要がある
⇨1周分、隣同士のデータを比較すればいい
⇨ n-1回だ
⇨n→∞の場合 最小値Ω(n) となる
⚪︎バブルソートのコード例
#include <cs50.h>
#include <stdio.h>
int main(void){
int array[] = {5, 2, 7, 4, 1, 6, 3, 0}; // 並び替えたい数字の配列
int arraylen = sizeof(array) / sizeof(array[0]); // 配列の要素数を取得
for (int j = 0; j < arraylen-1; j++){ // 要素数-1周確認するためのループ
int is_swapped = false; // 隣同士スワップしたかの初期化
for (int i = 0; i < arraylen-1; i++){ // 隣同士を比較するためのループ
if (array[i] > array[i + 1]){ // 大小比較
int tmp = array[i];
array[i] = array[i + 1];
array[i + 1] = tmp;
is_swapped = true;
}
}
if (!is_swapped){ // 1周分隣同士を比較して、1度もスワップしなければ処理終了
break;
}
}
for (int k = 0; k < arraylen; k++){ // ソート結果出力
printf("%i", array[k]);
}
printf("\n");
}
3-3. マージソート(merge sort)
検索における二分探索と似ている。配列を半分に分割、半分に分割、、、、1個になるまで実施。分割した左半分と右半分をソートして、マージ(統合する)→これを繰り返す
ex) 7 3 6 1 5 4 2 0のデータを並び替える
step 1: 配列を半分に分割 7 3 6 1 | 5 4 2 0
step 2: 分割したものをさらに半分に分割 7 3 | 6 1 | 5 4 | 2 0
step 3: さらに分割 7 | 3 | 6 | 1 | 5 | 4 | 2 | 0
step 4: 1個になるまで分割したので、ソートしてマージ(統合)する
元列: 7 | 3 | 6 | 1 | 5 | 4 | 2 | 0
1列: 3 7 | 1 6 | 4 5 | 0 2
step 5: 2個同士の配列をマージ(統合する)
元列: 7 | 3 | 6 | 1 | 5 | 4 | 2 | 0
1列: 3 7 | 1 6 | 4 5 | 0 2
2列: 1 3 6 7 | 0 2 4 5
step 6: 4個同士の配列をマージ(統合する)
元列: 7 | 3 | 6 | 1 | 5 | 4 | 2 | 0
1列: 3 7 | 1 6 | 4 5 | 0 2
2列: 1 3 6 7 | 0 2 4 5
3列: 0 1 2 3 4 5 6 7
※マージする時は、左右の配列の先頭同士を比較して、小さい方から並べていく
実行回数
データ数が n の場合
・上記のstep6にて、データが8個の場合に新たに使用した列数は3列→log(n)
・列ごとに1回は数字を確認する
したがって、実行回数 = n × log(n) = nlog(n)
n→∞でも省略される部分はないので、 最大値O(nlog(n))
次に最小値だが、最高の場合は配列がすでにソートされている状態だ
→しかし、ソートされているかを確認するには、結局全て見ないといけない
→したがって、 最小値Ω(nlog(n))
⚪︎マージソートのコード例
#include <cs50.h>
#include <stdio.h>
void merge_sort(int array[], int left, int right);
void merge(int array[], int left, int mid, int right);
int main(void){
int array[] = {5, 2, 7, 4, 1, 6, 3, 0}; // 並び替えたい配列
int arraylen = sizeof(array) / sizeof(array[0]); // 配列の要素数を取得
merge_sort(array, 0, arraylen- 1); // マージソートの関数
for (int k = 0; k < arraylen; k++){ // 並び替えた配列の出力
printf("%i", array[k]);
}
printf("\n");
}
void merge_sort(int array[], int left, int right){ // マージソート関数
if(left < right){
int mid = left + (right - left)/2; // 配列を半分に分ける
merge_sort(array, left, mid); // 左半分のマージソート再起処理
merge_sort(array, mid + 1, right); // 右半分のマージソート再起処理
merge(array, left, mid, right); // マージ(統合)を実施
}
}
void merge(int array[], int left, int mid, int right){ // マージ関数
int left_size = mid - left + 1;
int right_size = right - mid;
int left_array[left_size], right_array[right_size]; // 左半分と右半分の配列を用意
for (int i = 0; i < left_size; i++){ // 左半分の配列を取得
left_array[i] = array[left + i];
}
for (int i = 0; i < right_size; i++){ // 右半分の配列を取得
right_array[i] = array[mid + 1 + i];
}
int i = 0;
int j = 0;
int k = left;
while(i < left_size && j < right_size){ // 左右の配列の先頭の数字を比較してマージ
if(left_array[i] < right_array[j]){
array[k] = left_array[i];
i++; // マージされた場合次の様子へ
} else {
array[k] = right_array[j];
j++; // マージされた場合次の様子へ
}
k++;
}
while(i < left_size){ // 左半分が奇数個の場合、1個余ることがある
array[k] = left_array[i];
i++;
k++;
}
while(j < right_size){
array[k] = right_array[j]; // 右半分が奇数個の場合、1個余ることがある
j++;
k++;
}
}
3-4. ソートのまとめ
1~3で紹介したソートについてまとめる
| ソート名 | 最大値O | 最小値Ω | 使用例 |
|---|---|---|---|
| 選択ソート | n^2 | n^2 | 特になし、バブルソートの方が良い |
| バブルソート | n^2 | n | 高頻度でソートを行う場合に適している |
| マージソート | nlog(n) | nlog(n) | あまり、ソートを行わない時に適している |