今回は分類タスクについて基本的な手法である次の2つを紹介します。
- ロジスティック回帰
- ベイズ判別
問題設定
本記事では、以下の問題を考えます。
n個のd次元データ $x_1, x_2 ,\cdots, x_n \in \mathcal{R}^d$ がそれぞれあるクラス $i \in \{1,\cdots K\}$ に分類されているとします。このとき、新しい入力データ $x \in \mathcal{R}^d$ が与えられたときに自動的に $x$ のクラス $y \in \{1,\cdots K\}$ を分類できるようにしたいです。すなわち、
$$
f:R^d \rightarrow \{1,2,\cdots K\}
$$
なる分類器 $f$ を作ることを目標とします。
ロジスティック回帰
まずは、ロジスティック回帰についてです。
ロジスティック関数について
ロジスティック回帰はロジスティック関数が本質的な役割を果たすので、まずは以下のロジスティック関数 $L(x)$ を定義します。
$$
L(x) = \frac{1}{1+\exp(-x)}
$$
wolframalpha などでこの関数を可視化すると以下のような図が得られます。
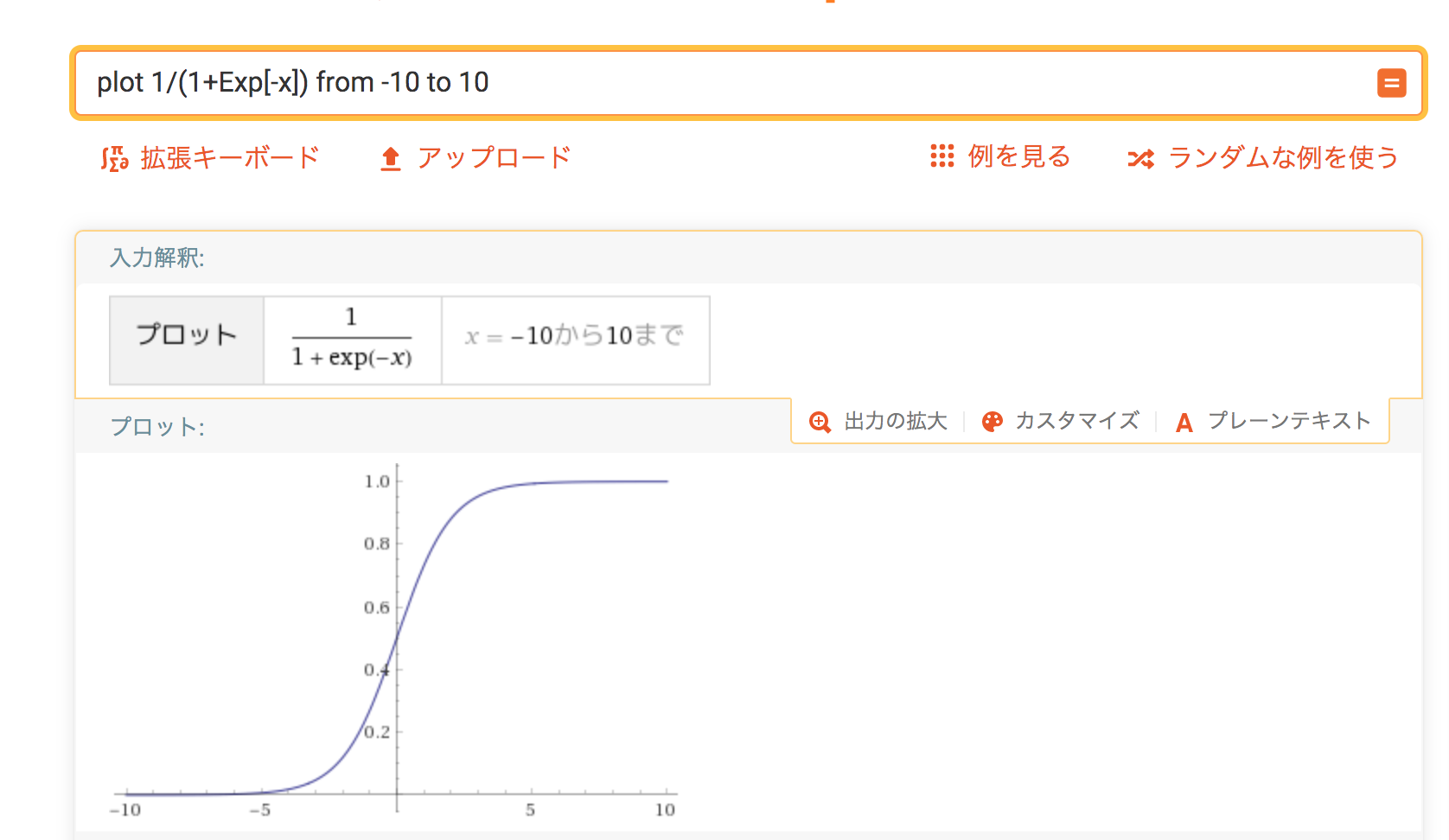
上の図からロジスティック関数は0から1までの値をとることがわかります。(ただしどんな値を入力しても0と1になることはない。)
アイデア
ロジスティック関数の出力値が0から1までの値をとることに着目して、この出力値をクラスに属する確率として表現することを考えます1。つまり、ロジスティック関数 $L$ をつかって、$x$がクラス $i \in \{1, \cdots K\}$ に属する確率 $\phi_i$ を求めます。もし、この確率 $\phi_i$ を求めることができれば、この確率が最大となるような $i$ を $x$ が属するクラスだと推定することにします。
すなわち、 $x$ の属するクラス $k$ は、
$$
k = argmax_{i \in \{1, \cdots K\}} \phi_i
$$
で求めることができます。
確率のモデル
次に、 $x$ が クラス $i \in \{1, \cdots K\}$ に入る確率 $\phi_i$ を求めるモデルを考えます。
ロジスティック関数 $L$ を使いたいので、各クラス $i$ に依存する加工 $g_i:\mathcal{R}^d \rightarrow \mathcal{R}$ を使って、
$$
(\phi_1 , \cdots, \phi_K ) =(L(g_1(x)), \cdots, L(g_K(x)))
$$
とするのが自然ですが、このままでは確率の和が1にならないので、
$$
(\phi_1 , \cdots, \phi_K ) =\frac{(L(g_1(x)), \cdots, L(g_K(x)))}{\sum L(g_i(x))}
$$
と正規化することにします2。 実は、これはニューラルネットワークの出力層で使われるソフトマックス関数と呼ばれるものです3。あとはこの加工 $g_i$ を考えればいいですが、普通は線形モデルで考えたいので、(d+1)*K個のパラメータ $\beta_i=(\beta_1^i, \cdots, \beta_d^i)^t, \beta_0^i \ \ (i= 1, \cdots , K)$をつかって以下のように表現します。
$$
g_i(x) = (\beta_i,x) + \beta^i_0 = \beta_1^ix_1 + \cdots \beta_d^i x_d + \beta_0^i
$$
ここで、 $(\beta_i,x)$ は $\beta_i$ と $x$ の内積です。行列で表現すると、以下のようにすっきりかけます。
$$
g(x) = (g_1(x), \cdots, g_K(x))^t = Wx + \beta_0
$$
ここで $W$ は、 $W$ の各行ベクトルが、 $(\beta_1^i, \cdots, \beta_d^i)$ となるK*dの行列で、 $\beta_0 = (\beta_0^1,\cdots, \beta_0^K)^t$ となります。
この式は、まさしくニューラルネットワークの更新式そのものですね。 ですので、私はロジスティック回帰のことを中間層なしニューラルネットワークと呼んでいます。4
パラメータの求め方
あとはパラメータである、 $W, \beta_0$ を求めることを考えます。これは、最尤法を使って求めます。つまり確率関数 $p(y=i;W,\beta_0,x)$ に対して、尤度関数 $p(W,\beta_0;y=i,x)$ を考え、尤度が最大となるパラメータ $W, \beta_0$ を求めます。確率関数は、$W,\beta_0$ は固定されていて確率を返すのに対して、尤度関数は $W, \beta_0$ が変数として動き、返り値は確率ではないことに注意しましょう。
確率関数、すなわち$x$ を入力したときの $y=i$ となる確率は前節で
$$
p(y=i;W,\beta_0,x) = \phi_i
$$
と求められました。これはカテゴリカル分布というもので、ベルヌーイ分布を多クラスに拡張したものです。確率関数は、
$$
p(y;W,\beta_0,x) = \Pi_{i=1}^{K} \phi_i^{y_i}
$$
と書き換えることができます。5ここで、 $y$ はワンホットベクトルすなわち、属するクラスの成分は1でそれ以外の成分は0になっているベクトルとします。
サンプル $(x_1,y_1) ,\cdots, (x_n,y_n)$ は独立だとすると、この事象が起こる確率は、
$$
\Pi_{j=1}^{N} \Pi_{i=1}^K \phi_{i,j}^{y_{i,j}}
$$
となります。ここで $\phi_{i,j}$ と $y_{i,j}$ はそれぞれ、$j$ 個目のデータ $x_j$ がクラス $i$ に属する確率、 $j$個目のデータ $x_j$ がクラス $i$ に入っているかどうかを表します。
$x_j, y_{i,j}$ をgivenとして、この式を尤度関数として $W, \beta_0$ に関して最大化すれば $W, \beta_0$ を求めることができます。6
注意
- ここでは、加工 $g$ を線形モデルにしましたが、非線形モデルやカーネルを使っても面白いかもしれないです。
- 損失関数や確率を求めるロジスティック関数に特に意味はないように思うので、ニューラルネットワークのようにいろいろいじっても面白いかもしれない。7
ベイズ判別
力尽きたので、また折を見て書きます。