数式の練習です。
二次ローパス・フィルタ
| 二次ローパス・フィルタ 回路図 |
|---|
 |
| 伝達関数 |
| $T(s)=\LARGE \frac{1}{1+s\frac{1}{Qω_0} + s^2\frac{1}{ω_0^2}} = \frac{1}{1+s\frac{2ζ}{ω_0} + s^2\frac{1}{ω_0^2}} = \frac{ω_0^2}{ω_0^2 + 2sζω_0 + s^2}$ |
| $( s はラプラス変数。 jω はsとする。 ω_0は角周波数(角振動数?)。 $ $ζは減衰係数。Q はフィルタのクオリティ・ファクタ。ζ = \frac{2}{Q}) $ |
| TeXの記述 |
$T(s)=\LARGE \frac{1}{1+s\frac{1}{Qω_0} + s^2\frac{1}{ω_0^2}} = \frac{1}{1+s\frac{2ζ}{ω_0} + s^2\frac{1}{ω_0^2}} = \frac{ω_0^2}{ω_0^2 + 2sζω_0 + s^2}$ |
$Q$の取る値によって、フィルタの特性は大きく変わります。$Q$が0.707より大きいと、フィルタ応答にピーキングが生じ、$Q$が0.707 より小さいと、カットオフ周波数$F_0$ でのロールオフが大きくなり、その勾配は緩やかなものとなり、早めに下がり始めます。
| $Q$ | ${\frac{{1}}{{2}}}$以下 | ${\frac{{1}}{{2}}}$ | ... | ${\frac{{1}}{{\sqrt{2}}}}$ =...0.707 | $ {\frac{{1}}{{\sqrt{2}}}}$以上 |
|---|---|---|---|---|---|
| ピーク | なし | なし | なし | なし | あり |
matlab
time_constant = 0.16; % 時定数
natural_freq = 1 / time_constant; % 固有角振動数 ωn
damping_ratio = 1.0 % ζ（ゼータ）減衰係数（ダンピング比）。１＞；実数解、1；実数解、・・・1/√2；複素数解、1/√2＜；複素数解、ピークあり
G = tf([0, 0, natural_freq^2], [1, 2 * damping_ratio * natural_freq, natural_freq^2])
h = bodeplot(G);
p = getoptions(h);
p.FreqUnits = 'Hz';
setoptions(h,p);
grid on
hold on
damping_ratio = 0.15 % ζ（ゼータ）減衰係数。１＞；実数解、1；実数解、・・・1/√2；複素数解、1/√2＜；複素数解、ピークあり
G2 = tf([0, 0, natural_freq^2], [1, 2 * damping_ratio * natural_freq, natural_freq^2])
h = bodeplot(G2);
p = getoptions(h);
p.FreqUnits = 'Hz';
setoptions(h,p);
hold off
nyquistplot(G);
hold on
nyquistplot(G2);
grid on
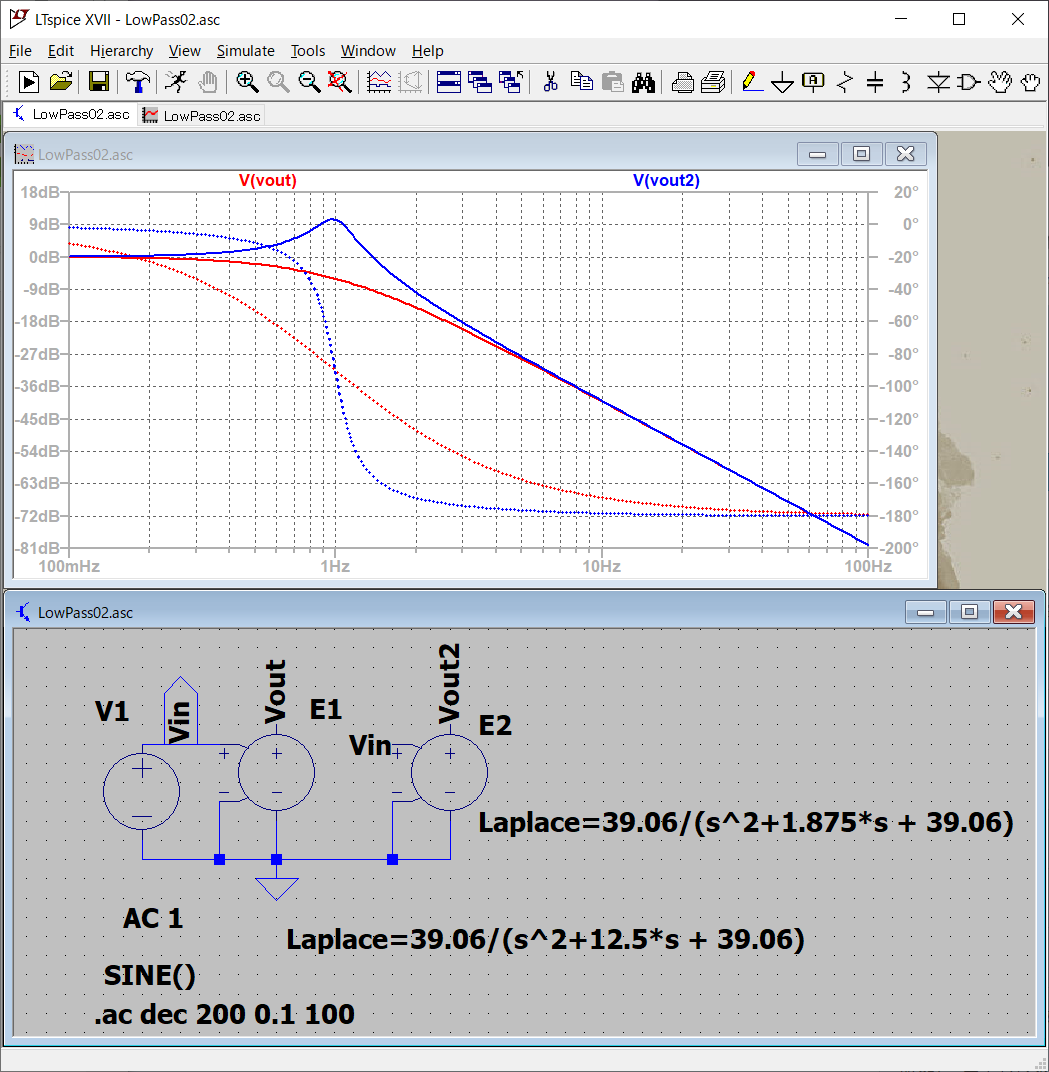
実行例です。
LTspice
V1の設定；
E1の設定；
E2の設定；
参考文献
環境
matlab R2021b update1（ホームライセンス）、tr関数はControl System Toolboxが必要。ラプラス関数のSymbolic Math Toolboxはホームライセンスでは購入できない。