【画像処理100本ノックに挑戦】Q.26. Bi-linear補間

使用したライブラリ

【画像処理100本ノック】独自の画像入出力クラスを作る

Q.26. Bi-linear補間

Bi-linear補間により画像を1.5倍に拡大せよ。

バイリニア補間は時々使っていますが、式の導出はしたことがなかったのでこの機会に考えてみます。

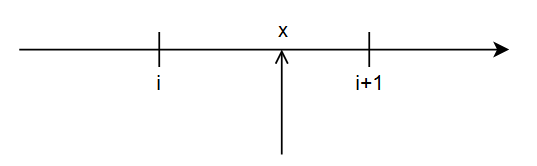
まず、簡単のために一次元で考えます。

上の図の$x=i$の位置の関数値$I(i)$及び、$x=i+1$の位置の関数値$I(i+1)$を既知とします。この間の位置$x$における関数値の推定が目的です。推定量は$x$の関数となるわけです。$x=i,i+1$における値を拘束条件とするだけでは条件を満たす関数はいくらでも存在するわけですが、一番簡単なのは一次関数です。一次関数に限定すれば、拘束条件を満たす関数は

I(x) = \{I(i+1)-I(i)\}(x-i) + I(i)

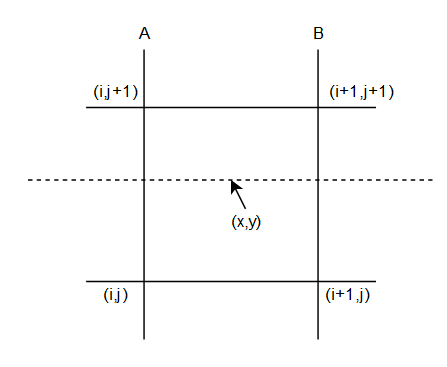
しかありません。二次元で考えます。

上図の直線A上で線形補間を考えれば

I(y;x=i) = \{I(i,j+1)-I(i,j)\}(y-j) + I(i,j)

となります。同様に直線B上では

I(y;x=i+1) = \{I(i+1,j+1)-I(i+1,j)\}(y-j) + I(i+1,j)

となります。点線上の左の点を$I(y;x=i)$とし、右の点を$I(y;x=i+1)$とします。この二つの点の間の点$(x,y)$の値はこれらの線形補間とします。

I(x,y) = \{I(y;x=i+1)-I(y;x=i)\}(x-i) + I(y;x=i)

これに具体的な式を入れてやればバイリニア補間の式となります。100本ノックの問題文に限らず、距離で重みづけする、という説明が多いですが、ここでいう距離は二次元ユークリッド距離でないことに注意が必要です。

int main()
{
	PPM ppm("imori.pnm");
	int width = ppm.Get_width();
	int height = ppm.Get_height();

	double a = 1.5;
	int Width = width * a, Height = height * a;

	PPM ppm2(Width, Height);

	auto LI = [&](double x, double Il, double Ir)
	{
		return (Ir - Il) * (x - (int)x) + Il;
	};
	
	for(int J=0; J<Height; J++)
		for (int I = 0; I < Width; I++)
		{
			double x = I / a;
			double y = J / a;
			int i = x, j = y;
			double dx = x - i, dy = y - j;
			if (i + 1 < width && j + 1 < height)
			{
				double Ir = LI(y, ppm(i + 1, j, 'r'), ppm(i + 1, j + 1, 'r'));
				double Il = LI(y, ppm(i, j, 'r'), ppm(i, j + 1, 'r'));
				ppm2(I, J, 'r') = LI(x, Il, Ir);
			}
			else ppm2(I, J, 'r') = ppm(i, j, 'r');

			if (i + 1 < width && j + 1 < height)
			{
				double Ir = LI(y, ppm(i + 1, j, 'g'), ppm(i + 1, j + 1, 'g'));
				double Il = LI(y, ppm(i, j, 'g'), ppm(i, j + 1, 'g'));
				ppm2(I, J, 'g') = LI(x, Il, Ir);
			}
			else ppm2(I, J, 'g') = ppm(i, j, 'g');

			if (i + 1 < width && j + 1 < height)
			{
				double Ir = LI(y, ppm(i + 1, j, 'b'), ppm(i + 1, j + 1, 'b'));
				double Il = LI(y, ppm(i, j, 'b'), ppm(i, j + 1, 'b'));
				ppm2(I, J, 'b') = LI(x, Il, Ir);
			}
			else ppm2(I, J, 'b') = ppm(i, j, 'b');
		}

	ppm2.Flush("out.ppm");
	return 0;
}

端っこの処理がいい加減ですが、まあよしとします。