背景
画像処理100本ノックに挑戦中です。
Q.36から離散コサイン変換(DCT)の問題です。DCTはよく知らなかったので少し調べてみました。
DCT-II
DCTにはいくつかバリエーションがあります。DCTの基底は実数のみで表されるところに特徴があります。フーリエ級数が実数成分のみとなるのは、関数が偶関数の場合なので、対象の関数を偶関数に拡張して定義します。離散フーリエ変換の場合、偶関数であることは要求せず、ただ周期的に拡張するだけでした。この拡張の仕方によってバリエーションがあります。
ここではDCT-IIを取り上げます。DCT-IIは
X_k = \sum_{n=0}^{N-1}x_n\cos\left\{\frac{\pi}{N}(n+\frac{1}{2}k)\right\}
で定義されます。Wikipediaを見てみると、$x_n$が$n=-1/2$に対して偶対称うんぬんかんぬんの境界条件に対応するとかよくわからないことが書いてあります。
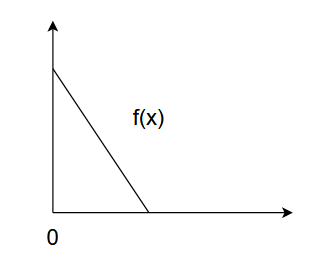
考えてみます。まず$x\geq0$で定義される$f(x)$を考えます。
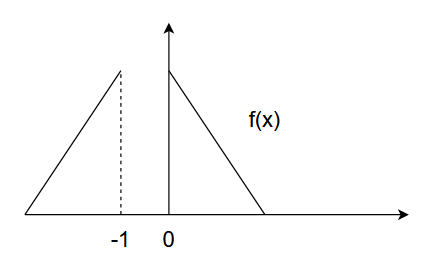
$x=-1/2$で偶対称になるように関数を拡張します。
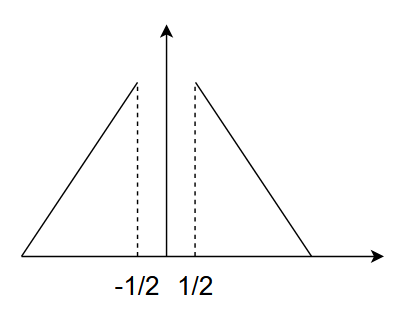
$x=0$が中心になるように平行移動します。
どうもDCT-IIはこういう感じの拡張をするようです。これを周期的に並べてフーリエ変換を考えればよいようです。
面倒なのでここではDCT-IIの導出はしませんが、ごりごりやれば出てきそうだな、というところまでは理解したいと思います。
$f(x)$が$0\leq x$で定義されているとして、次のような関数を定義します。
g(x) =
\begin{cases}
f(x-1/2) & x\geq 1/2\\
f(-x-1/2) & x\leq -1/2
\end{cases}
$g(x)$の$x=\frac{2n+1}{2}$の点を離散サンプリングします($n$は整数)。
\tilde g(x) = g(x)\sum_{n=-\infty}^{\infty} \delta(x-\frac{2n+1}{2})
$\tilde g$は偶関数なので、そのフーリエ変換は実となります。フーリエ変換してみます。
\begin{eqnarray}
\tilde G(\nu) &=& \int \tilde g(x)e^{-2\pi i\nu x} dx\\
&=& \int g(x)\sum_{n=-\infty}^{\infty} \delta(x-\frac{2n+1}{2})e^{-2\pi i\nu x} dx\\
&=& \sum_{n=0}^{\infty} f(n)\cdot 2\cos\left(2\pi\nu \frac{2n+1}{2}\right)
\end{eqnarray}
DCT-IIの式っぽいものが出てきました。ここでは周期化していないので、周期化すればDCT-IIの式と一致すると思われます。
DCT-IIとDFT
これでなんとなく、DCT-IIの式が導出できそうな感触がつかめました。
次に確認したいのは、DFTとの対応関係です。これがわかれば、FFTを用いて高速にDCTを計算することが出来ます。WikipediaによればDCT専用アルゴリズムの速度には敵わないようですが、実用的な問題はなさそうです。
Wikipediaの説明によれば、例えばデータがabcという実数列で表されるとき、DCT-IIはabccbaと拡張することに相当し、さらにDFTを用いて計算する際は0a0b0c0c0b0aとしてDFTすればよいそうです。この理由を考えてみます。
\tilde G(\nu) = \sum_n g(n+1/2)e^{-2\pi i\nu(n+1/2)}
を元に考えれば、DFTと同じ式に持っていくためには$n+1/2\equiv m/2$という置き換えをしてexpの指数部をDFTと同じ形にします。
\tilde G(\nu) = \sum_{m={\rm odd}} g(m/2)e^{-2\pi i\nu m/2}
DFTではm=oddという制限はないので、m=evenの点をゼロとして$g$を拡張してやればよいです。これが0を挿入する理由です。厳密な証明も難しくはありませんが、ここでは省略します。
まとめると、$N$点のデータ$x_n$があったとき、$4N$点の$y_n$を
\begin{eqnarray}
y_{2n+1} &=& y_{4N-2n-1}=x_n\;(0\leq n < N)\\
\end{eqnarray}
と定義してDFTすればDCT-II出来ます。上記の点以外はゼロとします。
DCT-IIの逆変換
DCT-IIの逆変換はDCT-IIIという変換です。DCT-IIIは
X_k = \frac{1}{2}x_0 + \sum_{n=1}^{N-1}x_n\cos\left\{\frac{\pi}{N}(k+1/2)\right\}
で与えられます。これは偶関数への拡張を${\rm abc}\to\rm{abc0\tilde c\tilde b\tilde a\tilde b\tilde c0cb}$という方法で行うことに相当します。ややこしいですが、DCT-IIの結果は自動的にこれを満たしますので、逆変換がDCT-IIIとなります。
まとめると、$N$点のデータ$x_n$があったとき、$4N$点の$y_n$を
\begin{eqnarray}
0\leq n<N&\to& y_n = x_n\\
n=N&\to& y_n = 0\\
N<n\leq 2N &\to& y_n = -x_{2N-n}\\
2N<n<3N &\to& y_n = -x_{n-2N}\\
n=3N &\to& y_n = 0\\
3N<n<4N &\to& y_n = x_{4N-n}
\end{eqnarray}
と定義してDFTすればDCT-II出来ます。上記の点以外はゼロとします。DCT-IIで変換後、フィルタ処理をしてDCT-IIIを行うときは、フーリエ空間上でこの対称性を満たす必要があることに注意を要します。
まとめ
離散コサイン変換とは何ぞやということがわかってきました。次回は実際にDCTしてみたいと思います。