背景
前回の記事で述べたように、標本分散の分散を記述するためにはは4次モーメントが必要となり少しややこしくなります。
標準正規分布については、平均周りの2次モーメントの標本分布はカイ二乗分布となります。今回はこれを数値実験で確かめます。
確かめたいこと
標準正規分布において、標本サイズを$n$、標本分散を$s^2$とすると、$ns^2$は自由度$n-1$のカイ二乗分布に従います。自由度$n-1$のカイ二乗分布とかいうカッコイイ名前ですが、これは$n-1$個の標準正規乱数を用意し、その二乗和の従う分布であり、それほどややこしいものではありません。
ここで確かめたいのは、標準正規乱数の二乗和がカイ二乗分布に従うこと、そして$ns^2$が自由度$n-1$のカイ二乗分布に従うことです。
数値実験1:標準正規乱数の二乗和がカイ二乗分布に従うことの確認
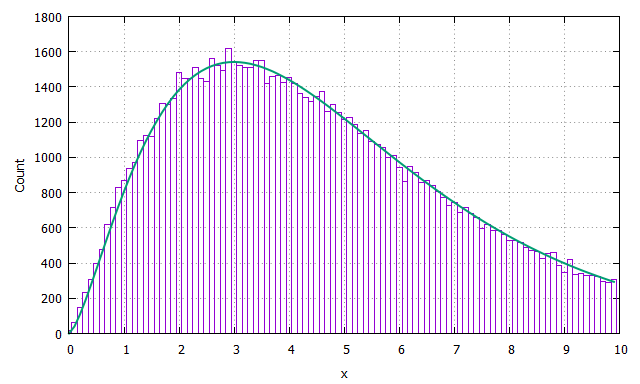
$5$個の標準正規乱数の二乗和をサンプリングしてヒストグラムを作ってみます。
# include <iostream>
# include <random>
# include <vector>
int main(int argc, char **argv)
{
std::mt19937 mt(0);
std::normal_distribution<double> r(0, 1);//標準正規乱数
int N = atoi(argv[1]);//標準正規乱数の個数
int Iter = 100000;//試行回数
for (int iter = 0; iter < Iter; iter++)
{
double sum = 0;
for (int n = 0; n < N; n++)
{
double X = r(mt);
sum += X * X;
}
std::cout << sum << std::endl;
}
return 0;
}
ヒストグラムと自由度$5$のカイ二乗分布を重ねてみます。おおむね一致していることが確認できました。
数値実験2:平均周りの二次モーメントが自由度n-1のカイ二乗分布に従うことの確認
標本サイズを$6$として、標本分散のサンプリングを行います。
# include <iostream>
# include <random>
# include <vector>
int main(int argc, char **argv)
{
std::mt19937 mt(0);
std::normal_distribution<double> r(0, 1);//標準正規乱数
int N = atoi(argv[1]);//標本サイズ
int Iter = 100000;//試行回数
for (int iter = 0; iter < Iter; iter++)
{
double sum2 = 0, sum1 = 0;
for (int n = 0; n < N; n++)
{
double X = r(mt);
sum1 += X;
sum2 += X * X;
}
std::cout << sum2-sum1*sum1/(double)N << std::endl;
}
return 0;
}
ヒストグラムと自由度$5$のカイ二乗分布を重ねてみます。おおむね一致していることが確認できました。
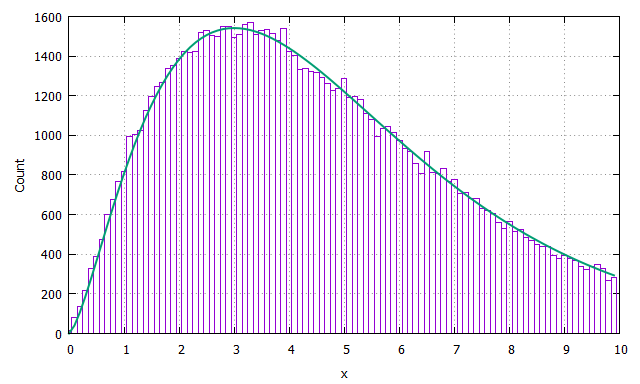
コードを見ると、そりゃあカイ二乗分布になりそうよな、と思います(sum1は平均ゼロでsum2の寄与が主だと思われるため)。
まとめ
標準正規乱数の二乗和がカイ二乗分布に従うこと、そして$ns^2$が自由度$n-1$のカイ二乗分布に従うことを数値実験で確認しました。
一般には$ns^2/\sigma^2$は自由度$n-1$のカイ二乗分布に従います。標本分散がわかっているものとして、$\sigma^2$の値として好きなものを取れば、$ns^2/\sigma^2$の値がカイ二乗分布のどこからサンプリングされるかが決まります。つまりその$\sigma^2$の値である確率がわかります。$\sigma^2$の値を網羅的に振ってやる(積分ですね)ことでどの範囲の$\sigma^2$の値があり得そうかがわかります。このようにすることで母分散の値を区間推定出来ます。