背景

最近は十分統計量について勉強していました。２、３日格闘してようやくわかってきた気がします。
個人のホームページなども色々見ていたのですが、よくわからないのは「十分統計量があれば元の確率分布を再構成出来る」というような説明です。具体的にどういうことなのかはっきりと書いてあるサイトを見つけられていませんが、試しに数値実験でそれらしいことをやってみることにします。

十分統計量とは

詳しい説明はここでは省きますが、データを$X$、任意の統計量を$T$で表したとき、
$$
P(X|T)
$$
が母数$\theta$を含まないとき$T$を十分統計量といいます。この条件を満たせば、$\theta$の推定に関して、$X$の代わりに$T$を用いても情報の欠落はありません。例えば正規分布では標本平均は母平均$\mu$に対する十分統計量です。このため、例えば${X_1,\cdots,X_{10}}$を得る操作を$100$回繰り返す場合を考えると、$\mu$の推定に限ればデータを全て記録しておく必要はなく、標本平均のみ記録しておけば十分ということになります。

母数を推定せずに母分布の概形を得る

母分布の概形を得る最も簡単な方法は$T$を元に母数を推定してしまうことです。しかしここではそれはしません。十分統計量$T$の意味するところは、推定の枠組みを$X$でなく$T$で記述出来るということだと思っています。つまり、主役を$p(X)$から$p(T)$に交代出来るということです。
具体的には
$$
P_\theta(X) = P(X|T)P_\theta(T)
$$
を用います。$P_\theta(T)$は母数を含んでいますが、観測により$T$の値のリストは持っていますので、そこから一様サンプリングすることにより$p(T)$からのサンプリングを模すことが出来ます。$P(X|T)$は定義より母数が含まれていませんので、関数形がわかっていれば素直に計算機で乱数生成出来ます。つまり手順は

観測値から計算された$T$の値のリストから一様乱数でひとつの値$t$を選択する
選んだ$t$を$P(X|T)$に代入し、母分布を$P(X|T)$とする乱数を計算機で生成する

となります。

数値実験

母平均$\lambda=5$のポアソン分布から値をサンプリングすることを考えます（最初は正規分布で数値実験する予定でしたが、連続分布は計算がややこしく、断念しました…）。簡単のため、標本サイズは$n=2$とします。十分統計量としては$T={X_0+X_1}$を考えます。
$p(x|t)=p(x,t)/p(t)$を利用して$p(x|t)$を求めます。$p(x,t)$は$x_0+x_1=t$を満たす場合以外はゼロですので、

p(x,t) = \left\{
\begin{array}{ll}
\frac{\lambda^{x_0}e^{-\lambda}}{x_0!}\frac{\lambda^{x_1}e^{-\lambda}}{x_1!} & (x_0+x_1=t) \\
0 & (\rm otherwise)
\end{array}
\right.

となります。$p_\theta(t)$は$x_0+x_1=t$を満たす組み合わせ全てですので

\begin{eqnarray*}
p_\theta(t) &=& \sum_{x_0,x_1\;(x_0+x_1=t)}\frac{\lambda^{x_0}e^{-\lambda}}{x_0!}\frac{\lambda^{x_1}e^{-\lambda}}{x_1!} \\
&=& \sum_{x_0=0}^t\frac{\lambda^{x_0}e^{-\lambda}}{x_0!}\frac{\lambda^{t-x_0}e^{-\lambda}}{(t-x_0)!}
\end{eqnarray*}

となります。$p(x|t)$には$\lambda$が含まれないはずですがそうなっているでしょうか。

$$
p(x|t) = \frac{1}{x_0!(t-x_0)!}\frac{1}{\sum_{n=0}^t\frac{1}{n!(t-n)!}}
$$

となり、$\lambda$が含まれないことを確認できました。
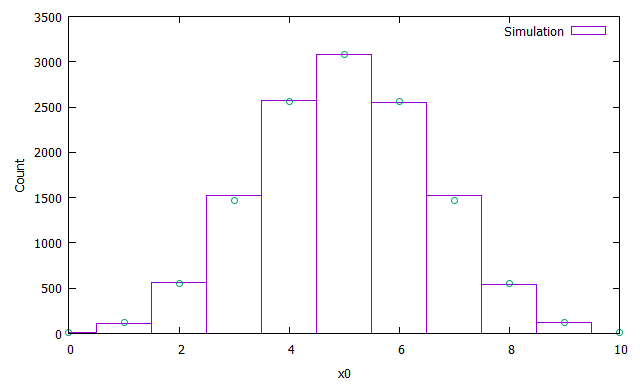
まずはここで計算した$p(x|t)$が正しいことを数値実験で確認します。$\lambda=5,t=10$としました。

#include <iostream>
#include <fstream>
#include <random>
#include <vector>

int factorial(int k)
{
        int ret = 1;
        for (int i=1; i<=k; i++)
        {
                ret *= i;
        }
        return ret;
}

int main()
{
        std::mt19937 mt(0);
        double lambda = 5;
        std::poisson_distribution<int> poi(lambda);

        int Iter = 100000;
        int t = 10;
        std::vector<int> data;
        for (int iter = 0; iter < Iter; iter++)
        {
                int x0 = poi(mt);
                int x1 = poi(mt);
                if (x0 + x1 == t) std::cout << x0 << std::endl;

        }
        auto pxt = [&](int x0)
        {
                double sum = 0;
                for(int n=0; n<=t; n++)
                {
                        sum += 1./factorial(n)/factorial((t-n));
                }
                double ret = 1./factorial(x0)/factorial(t-x0)/sum;
                return ret;
        };
        std::ofstream ofs("pxt.txt");
        for(int x0=0; x0<=t; x0++)
        {
                ofs << x0 << " " << pxt(x0) << std::endl;
        }

        return 0;
}

結果は次の通りです。

概ね一致する結果が得られました。

次は$p(x|t)$に従う乱数$x$の生成について考えます。これは$[0,1]$一様分布で生成した乱数の値を$r$として

\begin{eqnarray*}
0 \leq r < p(0|t) \to x&=&0\\
p(0|t) \leq r < p(0|t)+p(1|t) \to x&=&1\\
\vdots
\end{eqnarray*}

のようにすることで生成できます。試してみます。

#include <iostream>
#include <fstream>
#include <random>
#include <vector>

int factorial(int k)
{
        int ret = 1;
        for (int i=1; i<=k; i++)
        {
                ret *= i;
        }
        return ret;
}

int main()
{
        std::mt19937 mt(0);
        int t = 10;

        double den = 0;
        for(int n=0; n<=t; n++)
        {
                den += 1./factorial(n)/factorial(t-n);
        }

        std::vector<double> p;
        for(int x0=0; x0<=t; x0++)
        {
                double prob = 1./factorial(x0)/factorial(t-x0) / den;
                p.push_back(prob);
        }
        int Iter = 12300;
        std::uniform_real_distribution<double> r(0,1);
        for(int iter=0; iter<Iter; iter++)
        {
                double val = r(mt);
                double sum = 0;
                for(int x0=0; x0<=t; x0++)
                {
                        sum += p[x0];
                        if(val < sum)
                        {
                                std::cout << x0 << std::endl;
                                break;
                        }
                }
        }

        return 0;
}

出来ているようです。

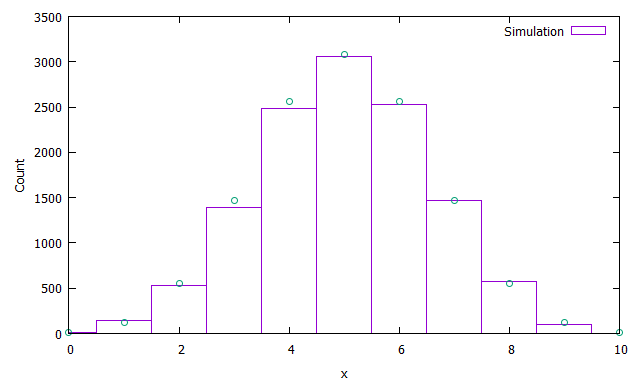
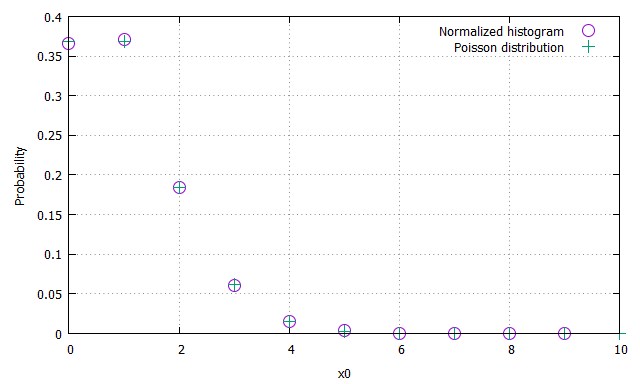
いよいよ$p_\theta(x)$の再現が出来るかやってみます。$\lambda=1$でやってみます。ポアソン分布から二つ値を取り出すことを10000回、$p(x|t)$から100000回繰り返してみます。

#include <iostream>
#include <random>
#include <vector>
#include <fstream>

int factorial(int k)
{
    int ret = 1;
    for (int i=1; i<=k; i++)
    {
        ret *= i;
    }
    return ret;
}

int main()
{
    double lambda = 1;
    std::mt19937 mt(0);
    int Iter = 10000;
    std::uniform_int_distribution<> r(0, Iter-1);
    std::poisson_distribution<> poi(lambda);


    std::vector<double> T;
    for (int iter = 0; iter < Iter; iter++)//観測
    {
        int x0 = poi(mt);
        int x1 = poi(mt);
        T.push_back(x0+x1);
    }

    std::uniform_real_distribution<double> u(0,1);

    auto pxt = [&](int t)
    {
        double den = 0;
        for(int n=0; n<=t; n++)
        {
            den += 1./factorial(n)/factorial(t-n);
        }
        std::vector<double> p;
        for(int x0=0; x0<=t; x0++)
        {
            double prob = 1./factorial(x0)/factorial(t-x0) / den;
            p.push_back(prob);
        }
        double val = u(mt);
        double sum = 0;
        for(int x0=0; x0<=t; x0++)
        {
            sum += p[x0];
            if(val < sum)
            {
                return x0;
                break;
            }
        }
    };

    for (int iter = 0; iter < 100000; iter++)//tをサンプリングしてp(x|t)で乱数生成
    {
        int i = r(mt);
        int t = T[i];
        int x0 = pxt(t);
        std::cout << x0 << std::endl;

    }

    std::ofstream ofs("poi.txt");
    for(int x0=0; x0<=10; x0++)
    {
        ofs << exp(-lambda)*pow(lambda,x0)/factorial(x0) << std::endl;;
    }
    return 0;
}

よく再現出来ています。ちなみに、元のデータ数が極端に少なかったり、$p(x|t)$から生成した乱数の数が少ないとポアソン分布からずれます。例えば観測数（=抽出した$t$の数）を100回まで減らしてみます。

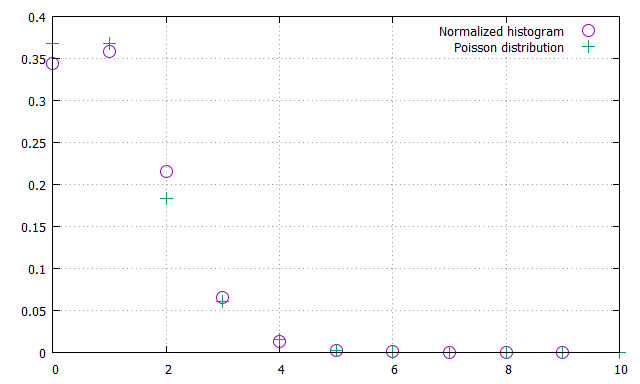
先程に比べるとずれが大きくなっていることが確認できました。

まとめ

個々のデータ$x$の値をリサンプリングすれば元の確率分布の概形が得られるわけですが、十分統計量からもリサンプリングにより元の確率分布を再現出来ることが確認できました。
個々のデータから母分布の概形を得る場合、母分布の関数形は未知でもよいわけですが、十分統計量の値をリサンプリングして母分布の概形を得る場合には母分布の関数形に関する知識が必要となります。同じ統計量でも、十分統計量かどうかは母分布の関数形に依存するため仕方がないのかもしれません。