使用したライブラリ
Q.23. ヒストグラム平坦化
ヒストグラム平坦化を実装せよ。
ヒストグラム平坦化とはヒストグラムを平坦に変更する操作であり、上記の平均値や標準偏差などを必要とせず、ヒストグラム値を均衡にする操作である。
画素値$z\to z'$の変換は
z' = \frac{z_{\rm max}}{S} \sum_{i=0}^z h(i)
で与えられるらしい。なんだこの式。
式の意味を考えてみる
式を少し書き換えてみます。$\sum_{i=0}^z h(i)/S$は累積分布関数なので
\sum_{i=0}^z h(i)/S \equiv p(z)
と定義します。するとヒストグラム平坦化の式は
z' = z_{\rm max}p(z)
と書けます。累積分布関数からアプローチするのが見通しがよさそうです。
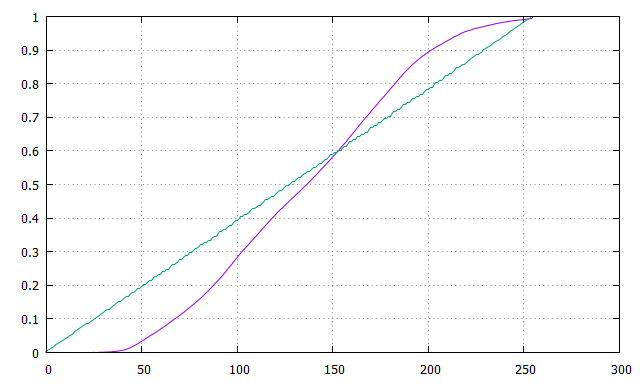
目的はヒストグラムを平坦化することでした。完全に平坦なヒストグラムの場合、累積分布関数は$z/z_{\rm max}$となります。なので、$z$をうまく変換して理想に近づけることを考えます。
ここでイメージをつかむため$f(x)=x^2$の線形化を考えます。そのためには、$f(x)=X$なる変数$X$を考えます。このような変数変換を行えば線形化が出来ます。
累積分布関数$p(z)$の話に戻ります。$p(z)$は一般に線形ではありませんが、先程の例に倣って
p(z) \equiv z'/z_{\rm max}
を満たす変数$z'$を考えます。これは元の式そのものですね。離散変数なので厳密な平坦化は一般には出来ませんが、さてどの程度効果があるかやってみます。
int main()
{
PPM ppm("imori.pnm");
int width = ppm.Get_width();
int height = ppm.Get_height();
int N = 256;
std::vector<int> hist(N);
std::vector<double> p(N);
for (int n = 0; n < N; n++)
{
hist[n] = 0;
p[n] = 0;
}
for (int j = 0; j < height; j++)
for (int i = 0; i < width; i++)
{
hist[ppm(i, j, 'r')]++;
hist[ppm(i, j, 'g')]++;
hist[ppm(i, j, 'b')]++;
}
for (int n = 0; n < N; n++)
for(int m=0; m<n+1; m++)
{
p[n] += hist[m]/(double)(3.*width*height);
}
std::ofstream ofs("p0.txt");
for (int n = 0; n < N; n++)
{
ofs << p[n] << std::endl;
}
int zmax = 255;
PPM ppm2(width, height);
for (int j = 0; j < height; j++)
for (int i = 0; i < width; i++)
{
ppm2(i, j, 'r') = zmax * p[ppm(i, j, 'r')];
ppm2(i, j, 'g') = zmax * p[ppm(i, j, 'g')];
ppm2(i, j, 'b') = zmax * p[ppm(i, j, 'b')];
}
for (int n = 0; n < N; n++)
{
hist[n] = 0;
p[n] = 0;
}
for (int j = 0; j < height; j++)
for (int i = 0; i < width; i++)
{
hist[ppm2(i, j, 'r')]++;
hist[ppm2(i, j, 'g')]++;
hist[ppm2(i, j, 'b')]++;
}
for (int n = 0; n < N; n++)
for (int m = 0; m < n + 1; m++)
{
p[n] += hist[m] / (double)(3. * width * height);
}
ppm2.Flush("out.ppm");
std::ofstream ofs2("p.txt");
for (int n = 0; n < N; n++)
{
ofs2 << p[n] << std::endl;
}
return 0;
}