確率分布を特徴づけるパラメータは平均と分散だけではない

平均と分散だけで確率分布を特徴づけられない理由

考えてみれば当たり前ですが、平均$\mu$と分散$\sigma^2$というふたつだけでは一般にパラメータが足りません。ガウス分布の場合はパラメータがふたつなので$\mu$と$\sigma^2$で完全に特徴づけることが出来ますが、テイラー展開を考えれば一般には無限個のパラメータが必要であり、明らかに不足です。

観測可能な量からどうやって確率分布を特徴づければよいか

確率密度関数が2次までの級数展開で表現出来ることがわかっているとします。
$$
f(x) = a_0 + a_1x + a_2x^2
$$
ここでは議論を簡単にするため、$-\beta<x<+\beta$の範囲の値のみとるものとします。まず、この範囲で積分して$1$である必要があります。
$$
\int_{-\beta}^{+\beta}f(x)dx = 2\beta a_0+\frac{2}{3}\beta^3 a_2 = 1
$$
さらに平均値(=1次モーメント)もわかっているものとします。
$$
\int_{-\beta}^{+\beta}xf(x)dx = \frac{2}{3}\beta^3a_1 = \mu_1'
$$
これで$a_1$が決定できました。さらに
$$
\int_{-\beta}^{+\beta}x^2f(x)dx = \frac{2}{3}\beta^3a_0+\frac{2}{5}\beta^5a_2 = \mu_2'
$$
もわかっているものとします(2次モーメント)。これらを連立して解けば$a_0,a_2$も決定できることがわかります。これから標本を元に$N$次モーメントまでわかれば、確率密度関数の$N$次テイラー近似が求まりそうです。

数値実験

分布関数として次のような分布関数を考えます。
$$
f(x) = \alpha(x+\beta)(x-\beta)
$$
分布関数の範囲は$[-\beta,+\beta]$とします。規格化条件より
$$
\int_{-\beta}^\beta f(x) dx = -\frac{4}{3}\alpha\beta^3 = 1
$$
でなければならないので、
$$
\alpha = -\frac{3}{4\beta^3}
$$
となります。数値実験のためには、このような分布関数に従う乱数が必要なので、棄却法という方法で生成します。一様乱数を発生させて、分布関数の内側に入れば採用、そうでなければ棄却するというシンプルなアルゴリズムです。ここでは詳細は割愛します。

#include <iostream>
#include <random>

int main()
{
        double beta = 1;
        double alpha = -3./4./beta/beta/beta;

        auto f = [&](double x)
        {
                return alpha * (x+beta) * (x-beta);
        };
        auto in_f = [&](double x, double y)
        {
                if(y<=f(x)) return true;
                else return false;
        };
        double ymax = f(0);
        std::mt19937 mt(0);
        std::uniform_real_distribution<double> r(0,1);
        int num_of_sample = 1000000;

        std::vector<double> data;

        for(int n=0; n<num_of_sample; n++)
        {
                double x,y;
                do
                {
                        double xr = r(mt);
                        double yr = r(mt);
                        x = -beta+2*beta*xr;
                        y = ymax*yr;
                }while(!in_f(x,y));
                data.push_back(x);
        }
        for(int n=0; n<num_of_sample; n++) std::cout << data[n] << std::endl;

        return 0;
}

$10^6$個のデータを生成しました。所望の乱数が得られていることを確認するため、ヒストグラムを作ってみます。

./a.out | gsl-histogram -1 1 100 > hist.txt

gsl-histogramコマンドは有名な科学計算ライブラリをインストールするとついてくるデモプログラムですが便利です。

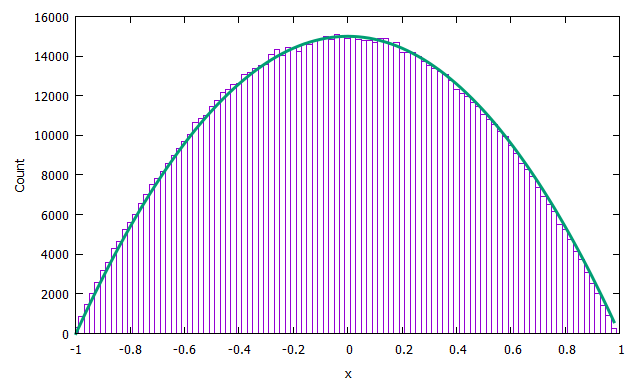
どうやら所望のデータが得られているようです。

さて、それではいよいよ生成した標本から元の分布関数を推定してみましょう。

#include <random>
#include <iostream>
#include <vector>

int main()
{
        std::vector<double> data;
        double tmp;
        while(std::cin >> tmp)
        {
                data.push_back(tmp);
        }
        int num_of_sample = data.size();

        double m1 = 0, m2 = 0;
        for(int n=0; n<num_of_sample; n++)
        {
                m1 += data[n] / (double)num_of_sample;
                m2 += data[n]*data[n] / (double)num_of_sample;
        }

        double beta = 1;
        double a[3];
        a[1] = m1*3./2./beta/beta/beta;
        a[2] = (beta*beta/3.-m2)/beta/beta/beta/beta/beta/(2./9.-2./5.);
        a[0] = (1.-2./3.*beta*beta*beta*a[2])/beta/2.;

        for(double x=-beta;x<=beta;x+=0.001)
        {
                std::cout << x << " " << a[0]+a[1]*x+a[2]*x*x << " " << -3./4./beta/beta/beta*(x+beta)*(x-beta) << std::endl;
        }
        return 0;
}

推定した分布関数と真の分布関数をプロットしてみます。

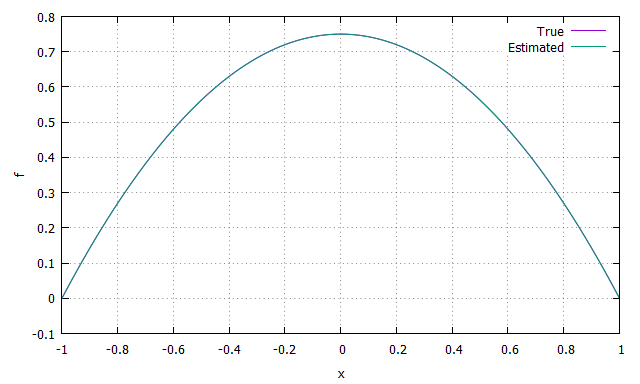
うまくいきました（ほとんど重なって区別がつきません）。ちなみに標本サイズを$10^3$まで減らした場合は次のようになりました。

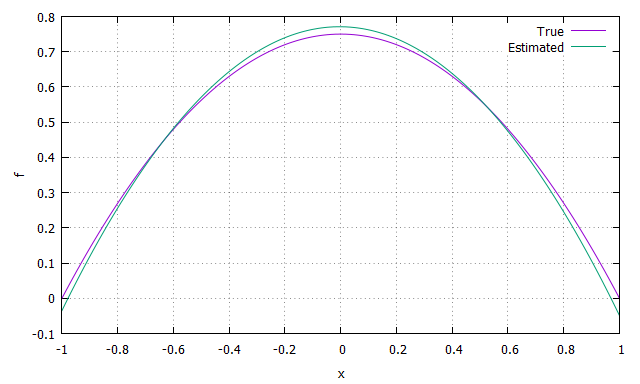
わずかにずれています。これは母集団のモーメントの推定誤差が原因であると考えられます。

まとめ

標本から度数分布を使わず分布関数を推定出来ました（実用性はない？）。モーメントを与えることで確率分布の特徴づけが出来そうです。確率分布を指定するためには普通、関数形といくつかのパラメータを与えますが、具体的な関数形を与えずとも代わりにモーメントを与えることで分布関数を指定出来そうです。
（2910/11/2追記）どうやらこの方法はモーメント法という方法らしいです。