概要
前回の記事で、インボリュート歯車のアニメーションを作成し、接触する歯の共通法線が動かないことを確認しました。
さらに歯車について理解を進めるため、法線が動いてしまう歯車を考えてみたいと思います。
また、ふたつの歯車の角速度の比と法線の動きが連動していることも確認します。
二次関数で歯を作る
接触を保つ条件は、滑らかな形状のもの同士について導かれるため、滑らかな形を考えることにします。二次関数なら計算が簡単そうなので、二次関数でやってみます。
具体的には、インボリュート歯車でひとつの歯を考え(つまり、反転/非反転のインボリュート曲線の組み合わせ)、歯の生えている座標を二点取り出します。二次関数はこの二点を通ることを要求します。そして、インボリュート曲線を伸ばしていって途中で止めます。歯先端で、反転/非反転の曲線が交わる前に止めると、歯が閉じません。そこで、反転/非反転の曲線同士を線分で接続します。二次関数は、そのような線分の中点を通ることを要求します。
下に凸な二次関数を考えるため、$\theta=3/2\pi$が中心に来るようなインボリュート歯を考えます。先ほど定義した線分の中点を$(X,Y)$とします。この点が二次関数の頂点(底)です。歯の生え始めの点を$(x',y')$とします。すると、二次関数は、
y = \frac{y'-Y}{(x'-X)^2} (x-X)^2+ Y
で与えられます。ほかの歯はこれを回転させればOKです。説明が難しいですが、コードを見ればなんとなくわかると思います。
角速度の比
歯車の中心軸を結ぶ線分を考えます。歯の共通法線がその線分を横切る点を考えます。その点と歯車の中心との距離の比で角速度が決定します。
実装
前回の記事ではずるをして、共通法線は解析的に計算して固定してしまいましたが、一般の曲線に対応するためには、数値的に計算する必要があります。今回はC++でSiv3Dを使って実装します。Siv3Dには曲線同士の交点を計算するメソッドが用意されていますので、これを利用することにします。前回同様Processingでやってもよいのですが、少し複雑な処理なので、実装しなおしても慣れているC++の方が楽だと判断しました。
#include <Siv3D.hpp> // Siv3D v0.6.15
#include <Siv3D/Geometry2D.hpp>
#include <fstream>
#include <vector>
const int width = 1000;
const int height = 600;
const int N = 150; // 曲線分割数
const int fps = 5;
bool approx = false;
Vec2 to_siv3dcoordinates(Vec2 v)
{
Vec2 ret(v.x + width / 2, -v.y + height / 2);
return ret;
}
Vec2 involute(double r, double theta, double phi0) // phi0: 開始点の位相
{
Vec2 ret;
ret.x = r * cos(theta + phi0) + r * theta * sin(theta + phi0);
ret.y = r * sin(theta + phi0) - r * theta * cos(theta + phi0);
return ret;
}
LineString involute(double r, Vec2 center, double phi0, double theta1, int sgn=1) // 二次近似したい
{
LineString ret;
// int N = 80;
double d_theta = theta1 / (double)(N - 1);
//Console << d_theta;
for (double theta = 0; theta <= theta1; theta += d_theta)
{
Vec2 pos = involute(r, sgn*theta, phi0)+ center;
pos = to_siv3dcoordinates(pos);
ret.push_back(pos);
}
return ret;
}
class Gear
{
private:
Vec2 center;
double r; // 基礎円半径
int z; // 歯数
double alpha; // 歯厚(radian)
double beta; // 歯間距離(radian)
double gamma; // beta = gamma * alpha
double theta1; // 歯長 [radian]
std::vector<LineString> v_inv;
Circle circle;
double angle;
std::vector<double> phi0;
bool approx;
void gen_involutes()
{
for (int i = 0; i < z; i++)
{
phi0[2*i] = i * (alpha + beta);
LineString inv = involute(r, center, phi0[2*i] + angle, theta1);
v_inv[2 * i] = inv;
phi0[2*i+1] = phi0[2*i] + alpha;
inv = involute(r, center, phi0[2*i+1] + angle, theta1, -1);
v_inv[2 * i + 1] = inv;
}
if(approx) gen_quadratic();
}
void gen_quadratic()
{
double X = center.x;
double Y = center.y - calc_tooth_length();
//Console << calc_tooth_length();
double x2 = r * cos(3. / 2. * Math::Pi + alpha/2.) + center.x;
double y2 = r * sin(3. / 2. * Math::Pi + alpha/2.) + center.y;
double a = (y2 - Y) / (x2 - X) / (x2 - X);
//int N = 50;
double dx = (x2 - X) / (double)(N - 1);
LineString qua0, qua1;
for (int i = 0; i < N; i++)
{
double x = X+i * dx;
double y = a * (x - X) * (x - X) + Y;
qua0.push_back(Vec2(x, y));
x = X - i * dx;
y = a * (x - X) * (x - X) + Y;
qua1.push_back(Vec2(x, y));
}
for (int i = 0; i < z; i++)
{
phi0[2 * i] = i * (alpha + beta)+this->angle;
LineString inv;
double angle = phi0[2*i] - (3. / 2. * Math::Pi - alpha / 2.);
//angle *= -1;
for (int i = 0; i < N; i++)
{
double x = qua0.at(i).x;
double y = qua0.at(i).y;
double x2 = (x - center.x) * cos(angle) - (y - center.y) * sin(angle) + center.x;
double y2 = (x - center.x) * sin(angle) + (y - center.y) * cos(angle) + center.y;
inv.push_back(to_siv3dcoordinates(Vec2(x2, y2)));
}
v_inv[2 * i] = inv;
phi0[2 * i+1] = i * (alpha + beta) + alpha + this->angle;
LineString inv2;
for (int i = 0; i < N; i++)
{
double x = qua1.at(i).x;
double y = qua1.at(i).y;
double x2 = (x - center.x) * cos(angle) - (y - center.y) * sin(angle) + center.x;
double y2 = (x - center.x) * sin(angle) + (y - center.y) * cos(angle) + center.y;
inv2.push_back(to_siv3dcoordinates(Vec2(x2, y2)));
}
v_inv[2 * i+1] = inv2;
}
}
double calc_tooth_length()
{
LineString inv0 = involute(r, center, phi0[0], theta1);
Vec2 pos0 = inv0.at(inv0.size() - 1);
LineString inv1 = involute(r, center, phi0[1], theta1);
Vec2 pos1 = inv1.at(inv1.size() - 1);
Vec2 peak_pos = (pos0 + pos1) / 2.;
return Geometry2D::Distance(to_siv3dcoordinates(center), peak_pos);
}
public:
Vec2 Get_center() const
{
return this->center;
}
Gear(double r, Vec2 center, int z, double gamma, double theta1, bool approx = false) : center(center), r{ r }, z{ z }, gamma{ gamma }, theta1{ theta1 }, circle(to_siv3dcoordinates(center), r), v_inv(2 * z), angle{ 0 }, phi0(2 * z), approx{ approx }
{
alpha = 2 * Math::Pi / (1 + gamma) / (double)z;
beta = gamma * alpha;
gen_involutes();
}
void rotate(double rotate_angle)
{
this->angle += rotate_angle;
gen_involutes();
}
void draw()
{
circle.draw();
for (int i = 0; i < 2 * z; i++)
{
v_inv[i].draw();
}
}
void write_image(Image& image)
{
circle.asPolygon().outline(CloseRing::Yes).overwrite(image, Palette::White);
for (int i = 0; i < 2 * z; i++)
{
v_inv[i].overwrite(image, Palette::White);
}
}
Vec2 normal(Vec2 pos) // posにおける接ベクトル
{
double min_dist = 1e15;
int imin;
for (int i = 0; i < 2 * z; i++)
{
double dist = Geometry2D::Distance(v_inv[i], pos);
if (dist < min_dist)
{
min_dist = dist;
imin = i;
}
}
min_dist = 1e15;
int jmin;
for (int j = 0; j < v_inv[imin].size(); j++)
{
double dist = Geometry2D::Distance(v_inv[imin].at(j), pos);
if (dist < min_dist)
{
min_dist = dist;
jmin = j;
}
}
Vec2 ret(0,0);
int N = v_inv[imin].size();
if (jmin > N * 0.05 && jmin < 0.95 * N) ret = v_inv[imin].normalAtPoint(jmin);
return ret;
}
friend double distance(const Gear& gear0, const Gear& gear1);
friend bool intersects(const Gear& gear0, const Gear& gear1);
friend Optional<Array<Vec2>> intersectsAt(const Gear& gear0, const Gear& gear1);
friend double intersects_d(const Gear& gear0, const Gear& gear1);
};
/*
double distance(const Gear& gear0, const Gear& gear1)
{
int z0 = gear0.z;
int z1 = gear1.z;
double min_dist = 1e15;
LineString a, b;
for(int i0=0; i0<2*z0; i0++)
for (int i1 = 0; i1 < 2 * z1; i1++)
{
//double dist = s3d::Geometry2D::Distance(gear0.v_inv[i0], gear1.v_inv[i1]); // ここでコンパイルが通らない
// double dist = s3d::Geometry2D::HausdorffDistance(a, b);
//Geometry2D::
//Geometry2D::Distance()
//if (dist < min_dist) min_dist = dist;
}
return min_dist;
}
*/
double to_0_2Pi(double phi)
{
while (phi > 2 * Math::Pi)
{
phi -= 2 * Math::Pi;
}
while (phi < 0)
{
phi += 2 * Math::Pi;
}
return phi;
}
bool intersects(const Gear& gear0, const Gear& gear1) // 歯車同士の交差判定
{
Optional<Array<Vec2>> opos = intersectsAt(gear0, gear1);
return opos.has_value();
/*bool ret = false;
int z0 = gear0.z;
int z1 = gear1.z;
for (int i0 = 0; i0 < 2 * z0; i0++)
for (int i1 = 0; i1 < 2 * z1; i1++)
{
double phi = gear0.phi0[i0] + gear0.angle;
phi = to_0_2Pi(phi);
bool isROI = (phi > Math::Pi * 1.85 && phi < Math::Pi * 0.15);
phi = gear1.phi0[i1] + gear1.angle;
phi = to_0_2Pi(phi);
isROI = (isROI && phi < Math::Pi * 1, 15 && phi > Math::Pi * 0.85);
isROI = true;
if (isROI && gear0.v_inv[i0].intersects(gear1.v_inv[i1]))
{
ret = true;
return ret;
}
}
return ret;*/
}
Optional<Array<Vec2>> intersectsAt(const Gear& gear0, const Gear& gear1) // 歯車同士の交差点を返す
{
Optional<Array<Vec2>> ret;
int z0 = gear0.z;
int z1 = gear1.z;
for (int i0 = 0; i0 < 2 * z0; i0++)
for (int i1 = 0; i1 < 2 * z1; i1++)
{
double phi = gear0.phi0[i0] + gear0.angle;
phi = to_0_2Pi(phi);
bool isROI = (phi > Math::Pi*1.15 || phi < Math::Pi*0.85);
phi = gear1.phi0[i1] + gear1.angle;
phi = to_0_2Pi(phi);
isROI = (isROI && phi < Math::Pi*1,15 || phi > Math::Pi*0.85);
//isROI = true;
if (isROI && gear0.v_inv[i0].intersects(gear1.v_inv[i1]))
{
ret = gear0.v_inv[i0].intersectsAt(gear1.v_inv[i1]);
return ret;
}
}
return ret;
}
double intersects_d(const Gear& gear0, const Gear& gear1)
{
Optional<Array<Vec2>> opos;
int z0 = gear0.z;
int z1 = gear1.z;
for (int i0 = 0; i0 < 2 * z0; i0++)
for (int i1 = 0; i1 < 2 * z1; i1++)
{
if (gear0.v_inv[i0].intersects(gear1.v_inv[i1]))
{
opos = gear0.v_inv[i0].intersectsAt(gear1.v_inv[i1]);
goto RET;
}
}
RET:
if (!opos.has_value()) return -1;
int N = (*opos).size();
if (N == 1) return 0;
else
{
return Geometry2D::Distance((*opos)[0], (*opos)[1]);
}
}
void Main()
{
Window::Resize(width, height);
double r = 140;
Vec2 center(-150,0);
int z = 11;
double gamma = 0.2;
Gear gear0(r, center, z, gamma, 0.335 * Math::Pi, approx);
center.x = center.x + 2 * r + 70;
Gear gear1(r, center, z, gamma, 0.335 * Math::Pi, approx);
Vec2 pos;
// 歯車同士の重なりが解消されるまで一方を回転させる
while (intersects(gear0, gear1))
{
gear1.rotate(0.01/2.);
}
// 再度接触するまで一方を回転させる
while (!intersects(gear0, gear1))
{
gear1.rotate(0.001);
}
std::ofstream ofs("data.txt");
VideoWriter writer{ U"output.mp4", Size(width, height), fps};
Image image{ width, height, Palette::Black };
DynamicTexture dtexture;// { image };
while (System::Update())
{
//gear0.draw();
//gear1.draw();
image.fill(Palette::Black);
dtexture.fill(image);
gear0.write_image(image);
gear1.write_image(image);
LineString lines;
lines.push_back(to_siv3dcoordinates(gear0.Get_center()));
lines.push_back(to_siv3dcoordinates(gear1.Get_center()));
Optional<Array<Vec2>> opos = intersectsAt(gear0, gear1);
bool write_data = false;
if (opos.has_value())
{
pos = Vec2(0, 0);
for (int n = 0; n < (*opos).size(); n++)
{
pos += (*opos)[n];
}
pos /= (double)(*opos).size();
Circle cir(pos, 2);
//cir.draw();
cir.overwrite(image, Palette::White);
Vec2 nvec0 = gear0.normal(pos);
Vec2 nvec1 = gear1.normal(pos);
if (nvec0 != Vec2(0, 0) && nvec1 != Vec2(0, 0))
{
write_data = true;
Vec2 nvec = pos + 5 * r * (nvec0 - nvec1);
Line line0(pos.x, pos.y, nvec.x, nvec.y);
Optional<Array<Vec2>> oposc = lines.intersectsAt(line0);
if (oposc.has_value())
{
//Console << (*oposc)[0];
double len = std::abs(gear0.Get_center().x - gear1.Get_center().x);
ofs << std::abs(to_siv3dcoordinates(gear0.Get_center()).x - (*oposc)[0].x) / std::abs(to_siv3dcoordinates(gear1.Get_center()).x - (*oposc)[0].x) << " ";
}
nvec = pos - 5 * r * (nvec0 - nvec1);
Line line1(pos.x, pos.y, nvec.x, nvec.y);
oposc = lines.intersectsAt(line1);
if (oposc.has_value())
{
//Console << (*oposc)[0];
double len = std::abs(gear0.Get_center().x - gear1.Get_center().x);
ofs << std::abs(to_siv3dcoordinates(gear0.Get_center()).x - (*oposc)[0].x) / std::abs(to_siv3dcoordinates(gear1.Get_center()).x - (*oposc)[0].x) << " ";
//Print << std::abs(to_siv3dcoordinates(gear0.Get_center()).x - (*oposc)[0].x) / std::abs(to_siv3dcoordinates(gear1.Get_center()).x - (*oposc)[0].x);// << " ";
}
line0.overwrite(image, Palette::White);
line1.overwrite(image, Palette::White);
}
}
double omega0 = 0.03;
gear0.rotate(omega0); // 一方は等速運動
//gear1.rotate(-omega0); // 一方は等速運動
//gear1.rotate(-0.01);
// 再度接触するまで一方を回転させる
double omega = 0;
double d_omega = 0.001;
while (intersects(gear0, gear1))
{
gear1.rotate(-d_omega);
omega += d_omega;
}
while (!intersects(gear0, gear1))
{
gear1.rotate(d_omega);
omega -= d_omega;
}
if(write_data) ofs << omega/omega0 << std::endl;
//System::Sleep(50);
dtexture.fill(image);
dtexture.draw();
writer.writeFrame(image.grayscale());
}
}
動画にしてみました。
数値計算なので、インボリュート曲線でも若干法線がふらついていますが、二次関数に比べると圧倒的に安定していることがわかります。
次に、角速度の経時変化を比べてみます。ついでに、法線と中心軸を結ぶ線分の交点から予測される角速度比も一緒にプロットしてみます。
まずはインボリュート曲線から。
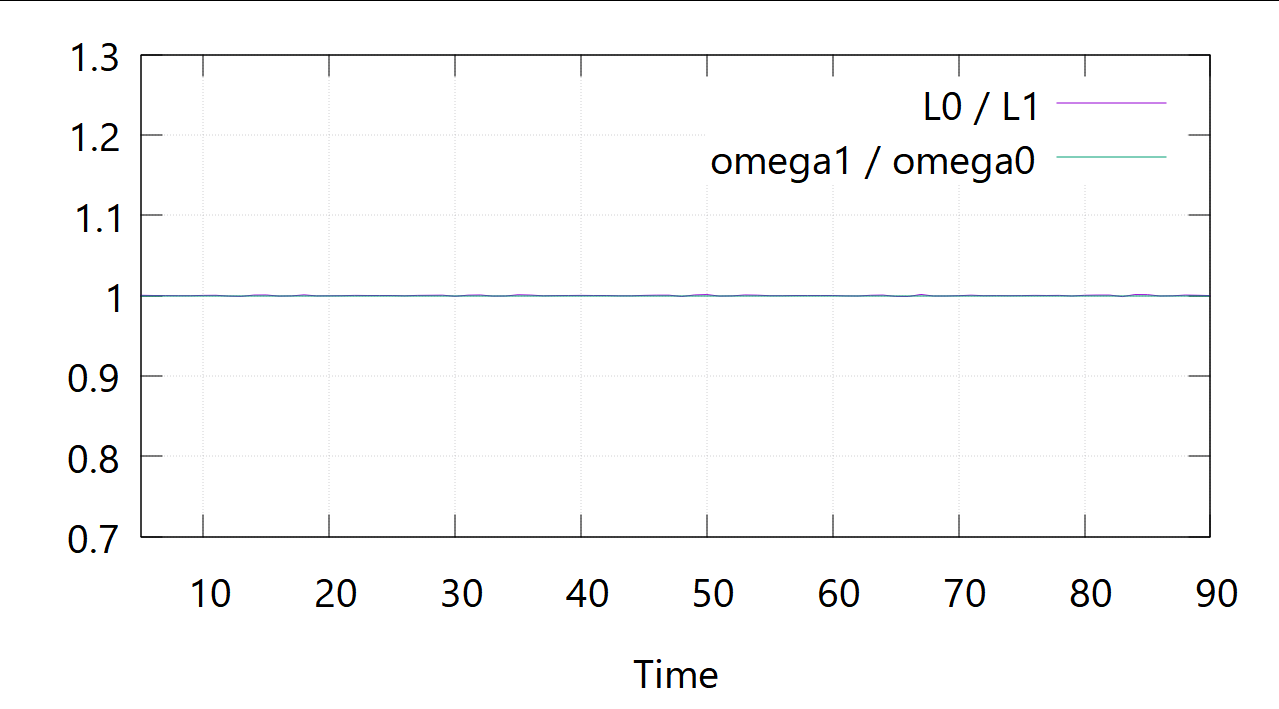
このスケールではほとんど一定ですね。
次に二次関数。
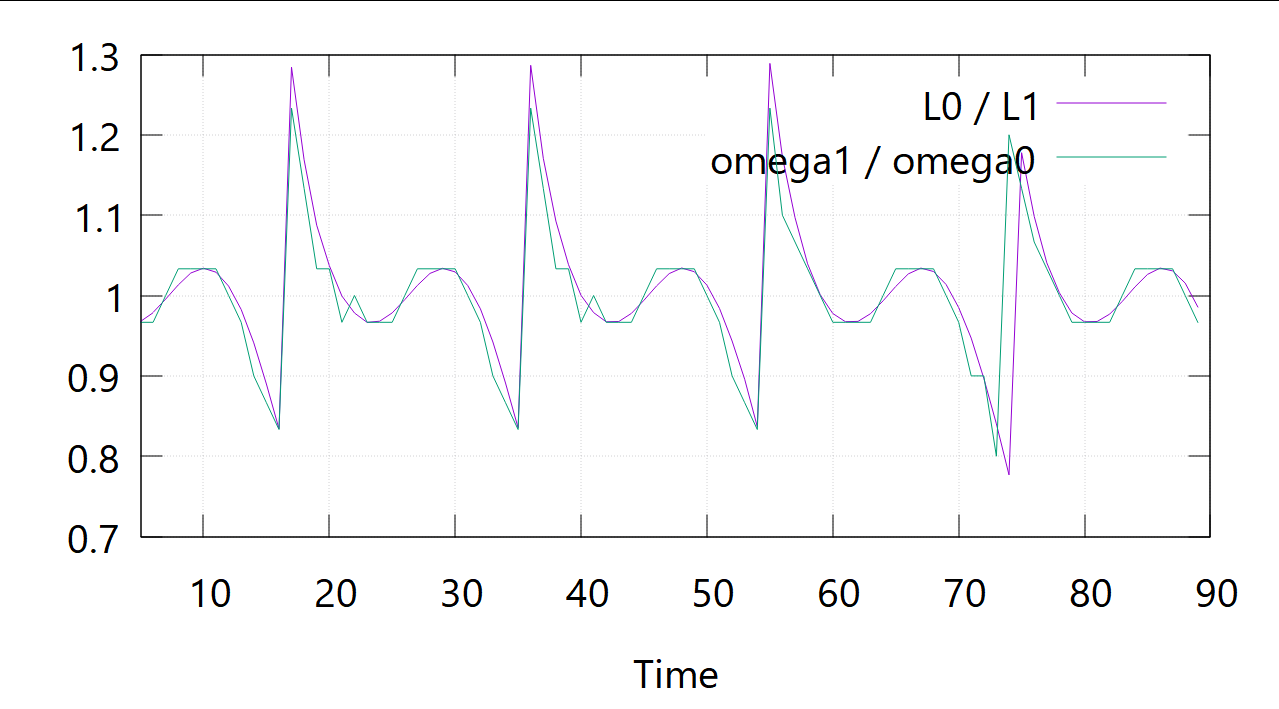
すごくふらついていることがわかります。インボリュート曲線が優れていることがわかりますね。
おわりに
それらしい結果を得るために、細かな気遣いが必要で、少々時間を要しました。歯車についてまた理解が進んだ気がします。