背景
前回(【区間推定】信頼区間の解釈、構成法について数値実験してみる)は尤度比検定を用いて信頼区間を構成しました。
「現代数理統計学」(竹村彰通)(以後教科書)の9章5節では最尤推定量を利用した近似的な信頼区間の構成法について述べられています。この方法はフィッシャー情報量と最尤推定量があれば汎用的に使えるため便利そうです。数値実験してみます。
最尤推定量の漸近的な性質を利用する
最尤推定量は標本サイズ$n$が大きいとき、近似的に平均$\theta$(母数)、分散$1/(nI(\theta))$の正規分布に従います。$I(\theta)$はフィッシャー情報量です。よって、統計量$\sqrt{nI(\theta)}(\hat\theta_n-\theta)$は標準正規分布に従い、$z_{\alpha/2}$を標準正規分布の両側$\alpha$点とすると、
-z_{\alpha/2}<\sqrt{nI(\theta)}(\hat\theta_n-\theta) < z_{\alpha/2}
に$1-\alpha$の確率で入ります。これを$L<\theta<R$の形にすれば信頼区間がわかります。
数値実験
ポアソン分布から$n$個の数をサンプリングし、$\lambda$を区間推定します。フィッシャー情報量は
I(\lambda) = 1/\lambda
です(計算は省略します)。$\lambda$の最尤推定量は$\hat\lambda_n = \bar x$です。
-z_{\alpha/2} < \sqrt{n/\lambda}(\bar x-\lambda) < z_{\alpha/2}
を$L<\lambda<R$の形に変形することを考えます。しかし、$1/\sqrt\lambda$がやっかいです。教科書で紹介されている近似法では、$n$が十分に大きければ$\lambda \simeq \bar x$が期待されますので、$I(\lambda)\simeq I(\bar x)$とします。こうすれば
\bar x - \sqrt{\bar x/n}z_{\alpha/2} < \lambda < \bar x + \sqrt{\bar x/n}z_{\alpha/2}
となりますので、信頼区間が求まります。
教科書には書いてありませんが、せっかく目の前にこの教科書が書かれた当時には信じられない性能を持つ計算機がありますので、網羅的に不等式を満たす$\lambda$を探索する方法も試してみたいと思います。$\lambda=3,\alpha=0.05$とします。$z_{\alpha/2}\simeq 1.96$となります。標本サイズは$n=5$としました。
# include <iostream>
# include <fstream>
# include <random>
# include <vector>
int factorial(int k)
{
int ret = 1;
for (int i = 1; i <= k; i++)
{
ret *= i;
}
return ret;
}
int main(int argc, char **argv)
{
std::mt19937 mt(0);
double lambda = 3;
int N = 100;//標本サイズ
std::poisson_distribution<int> poi(lambda);
double alpha = 0.05;
double z = 1.96;
int Iter = 100;
std::ofstream ofs0("aprox.txt");
std::ofstream ofs("loop.txt");
for (int iter = 0; iter < Iter; iter++)
{
std::vector<int> data(N);
double av = 0;
for (int n = 0; n < N; n++)
{
data[n] = poi(mt);
av += data[n] / (double)N;
}
double l, r;
l = av - sqrt(av / (double)N) * z;
r = av + sqrt(av / (double)N) * z;
double L, R;
for (double lambda0 = 0; lambda0 < 20; lambda0 += 0.01)
{
if (-z<sqrt((double)N/lambda0)*(av-lambda0) && z > sqrt((double)N / lambda0) * (av - lambda0))
{
L = lambda0;
break;
}
}
for (double lambda0 = 20; lambda0 >= 0; lambda0 -= 0.01)
{
if (-z<sqrt((double)N / lambda0) * (av - lambda0) && z > sqrt((double)N / lambda0) * (av - lambda0))
{
R = lambda0;
break;
}
}
ofs0 << iter << " " << av << " " << l << " " << r << std::endl;
ofs << iter << " " << av << " " << L << " " << R << std::endl;
}
return 0;
}
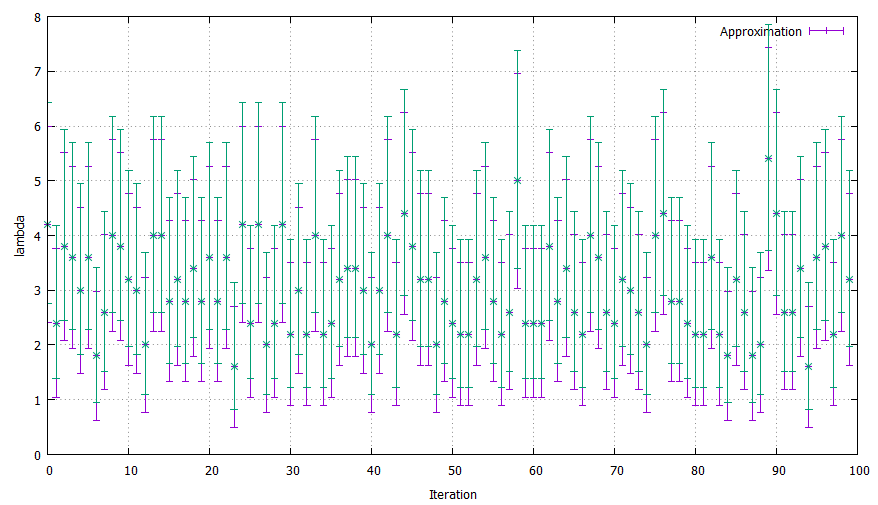
標本サイズが小さい割にはフィッシャー情報量を近似しても大きな差はありません。意外でした。$n=100$まで増やしてみます。

前回行った尤度比検定の結果とそれほど変わらないように見えます。教科書によりますと、近似なので$\alpha$からやや離れてしまうこともあるということですが、今回はよい結果が得られていると思います。
今後
とりあえずここで区間推定の勉強は一区切りとします。本当は、ブートストラップ法との比較などもしたいのですが、教科書を一通り読んでしまうことを優先します。その後にブートストラップ法との比較等もしたいと思っています。