描画パッケージGLSCを用いてSinカーブを描画してみよう

#はじめに
C言語の練習としてSinカーブを描画することはよく行われることであり、その方法は様々です。今回はGLSCという描画パッケージを用いて行います。

##GLSCとは
GLSCとは科学技術計算における描画ライブラリです。龍谷大学理工学部数理情報学科の研究グループが開発したもので、シミュレーションの結果の可視化に有用なライブラリです。
言語はC（もしくはFORTRAN,C++） で書きます。このページではC言語を用いて解説します。なお、インストールや細かい特徴、文法の解説に関しては割愛させていただきます。

##Sinカーブ
$y=sin(x)$ で表されるSinカーブですが、今回のプログラムでは

• 配列Yを用意して
• $x$ の $[0,2\pi]$ において 区間を100分割し
• $i$番目の値を$\frac{2\pi}{100}\times{i}$　で導出し($i\in\mathbb{N}$, $[1,100]$)
• その値を$y=sin(x)$ に代入して配列Yに格納し、
• 配列Yの値をプロットするプログラム (g_data_plot) を用いて描画します。

砕いて言うと、$[0,2\pi]$区間で等間隔100個のxの値を取りそれぞれ$y=sin(x)$に代入してyの値を取り、それを配列Yに格納してg_data_plotで描画する、と言うことです。

#描画画面を出す

initialize.c

#include <stdio.h>
#include <glsc.h>
int main(){
  //メイン関数内に描画画面の初期設定を記述
  g_init("GRAPH", 200.0, 200.0); //("GRAPH",標準座標のX,標準座標のY)
  g_device(G_DISP);
  g_sleep(G_STOP);
  g_term();
  return 0;
}

これでとりあえず描画画面が出ます。

#仮想座標を使ってみよう
GLSCには標準座標系の他に仮想座標系と言うものが存在します。標準座標系は左上に原点があり、どこまで使うかは上のプログラムにも記述されている通り、g_init("GRAPH", 200.0, 200.0);によって定めます。
仮想座標系は標準座標系を用いて範囲を決めて、その枠の中の座標の取り方を自分で決めることができます。仮想座標系は標準座標系のなかにいくつも宣言することができて、複数の動的な描画を行う際に使うことができます。

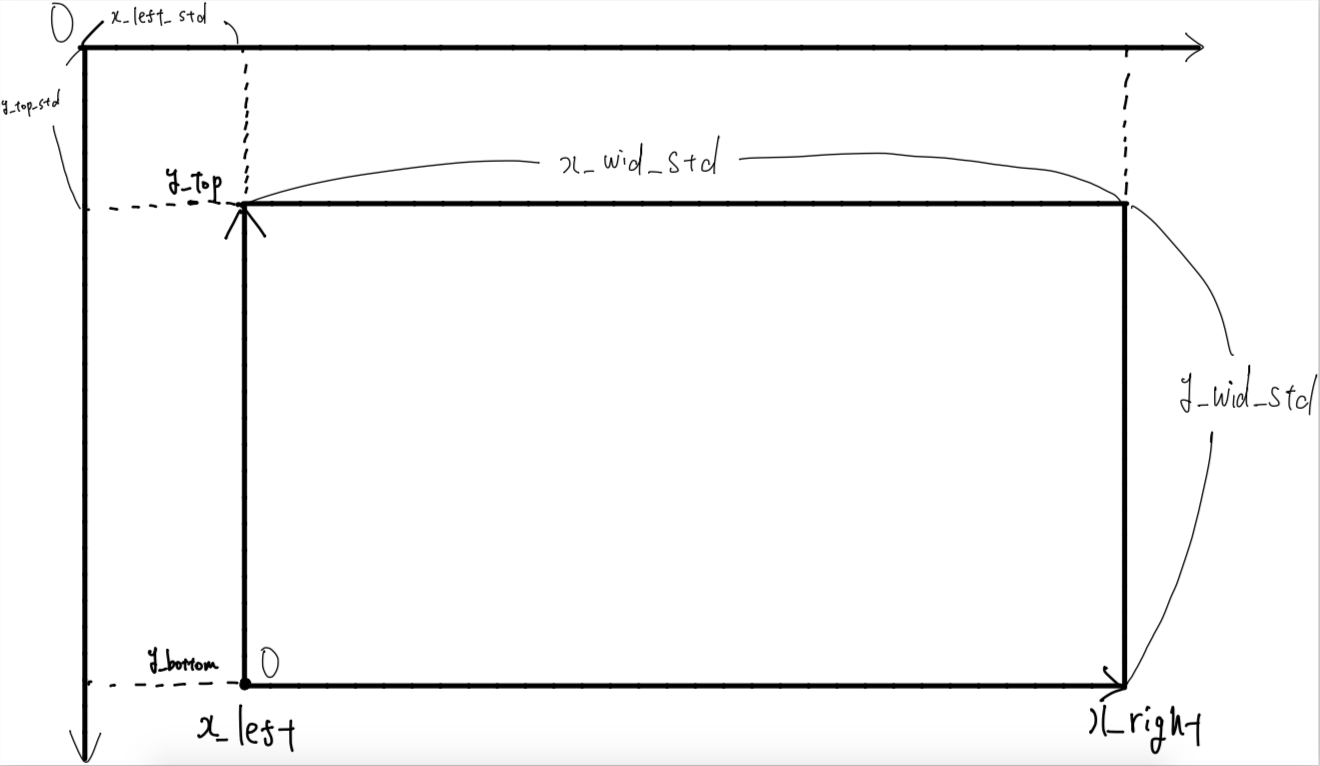
下の図の内側にある四角形が仮想座標系の取る範囲です。

手書きですみません...

##仮想座標系を定義する
以下をメイン関数内のg_deviceとg_sleepの間に記述します。

virtual.c

//仮想座標系の定義
  g_def_scale(1, 0.0, L, -1.0, 1.0, 10.0, 10.0, 180.0, 80.0);
  g_def_scale(2, 0.0, L, -1.0, 1.0, 10.0, 110.0, 180.0, 80.0);
//g_def_scale(仮想座標の番号,x_left,x_right,y_bottom,y_top,x_left_std,y_top_std,x_wid_std,y_wid_std)

x_left,x_right,y_bottom,y_topは仮想座標であり任意に定めることができて、x_left_std,y_top_std,x_wid_std,y_wid_stdは標準座標であり、これが仮想boxの大きさを決定します。

仮想座標を用いる場合には必ず以下を宣言しなければなりません。

scale.c

  g_sel_scale(1);//（括弧の中は仮想座標の番号）

組み込んでみると、こう↓。

virtual_main.c

#include <stdio.h>
#include <glsc.h>
int main(){
  //メイン関数内に描画画面の初期設定を記述
  g_init("GRAPH", 200.0, 200.0); //("GRAPH",標準座標のX,標準座標のY)
  g_device(G_DISP);
  //仮想座標系の定義
  g_def_scale(1, 0.0, L, -1.0, 1.0, 10.0, 10.0, 180.0, 80.0);
  g_def_scale(2, 0.0, L, -1.0, 1.0, 10.0, 110.0, 180.0, 80.0);
  g_sel_scale(1);//（括弧の中は仮想座標の番号）
  g_sel_scale(2);
  //ここに仮想座標系を用いた描画プログラムを記述
  g_sleep(G_STOP);
  g_term();
  return 0;
}

これで仮想座標系が定義されました。
#Sinカーブを描画
##静的なSinカーブを描画
動的な描画を行う前に静的な描画を試みます。
流れとしては、

• dx=L/(N-1) を定義 ($\because L=2\pi $)　
• 仮想座標系の定義
• 仮想座標を使う宣言
• 箱を定義
• x軸y軸を記述
• 配列Yを定義
• g_data_plotで描画

という順になります

---

dxを定義

dx.c

  double dx;
  //dxを計算
  dx = L/(N - 1);

仮想座標の中にsinカーブを描画する箱(box)を定義します。
色の種類は黒,白,赤,青,黄色,緑,シアン,マゼンタ。原色の他に三原色から色を生成することも可能です。詳しくはGLSCマニュアルを参照。

config.c

  g_area_color(G_WHITE);//(エリアの中の色:G_HOGE この場合は箱の中を指す。)

  g_line_color(G_BLACK);//(ラインの色:G_HOGE)

  g_line_width(2);//(ラインの太さ)

  g_box(0.0, L, -1.0, 1.0, G_YES, G_YES);
//(<仮想x座標>,<仮想y座標>,<縁を塗るか><中を塗るか>)
//中を塗らない、縁を塗らない場合は　G_NO　と記述

続いてx軸y軸の描画
g_move()が始点でg_plot()が終点です。

line.c

  //x軸
  g_move(0.0, 0.0);
  g_plot(L, 0.0);

  //y軸
  g_move(L/2.0, 1.0);
  g_plot(L/2.0, -1.0);

ここで配列Yを作る

sin.c

  for(i = 0; i < N; i++){
    Y[i] = sin(i*dx);
  }

この配列を用いてg_data_plotで描画することができます。

plot.c

//カレント座標系における左端から右端まで範囲を指定し配列YをN個表示するので配列Xは不要
  g_data_plot(0.0, L, Y, N);
//(<カレントX座標>,配列名,配列の要素数);

完成したプログラムがこれ↓。

sin_curve.c

#include <stdio.h>
#include <glsc.h>
#include <math.h>
#define L (2 * M_PI) //あとで使うので.
#define N (100)
int main(){
  double dx,Y[N];
  int i;
  //dxを計算
  dx = L/(N - 1);
  //メイン関数内に描画画面の初期設定を記述
  g_init("GRAPH", 200.0, 200.0); //("GRAPH",標準座標のX,標準座標のY)
  g_device(G_DISP);
  //仮想座標系の定義
  g_def_scale(1, 0.0, L, -1.0, 1.0, 10.0, 10.0, 180.0, 80.0);
  g_def_scale(2, 0.0, L, -1.0, 1.0, 10.0, 110.0, 180.0, 80.0);
  g_sel_scale(1);
  g_area_color(G_WHITE);
  g_line_color(G_BLACK);
  g_line_width(2);
  g_box(0.0, L, -1.0, 1.0, G_YES, G_YES);
  //x軸
  g_move(0.0, 0.0);
  g_plot(L, 0.0);

  //y軸
  g_move(L/2.0, 1.0);
  g_plot(L/2.0, -1.0);

  for(i = 0; i < N; i++){
      Y[i] = sin(i*dx);
  }
  g_data_plot(0.0, L, Y, N);
  g_sleep(G_STOP);
  g_term();
  return 0;
}

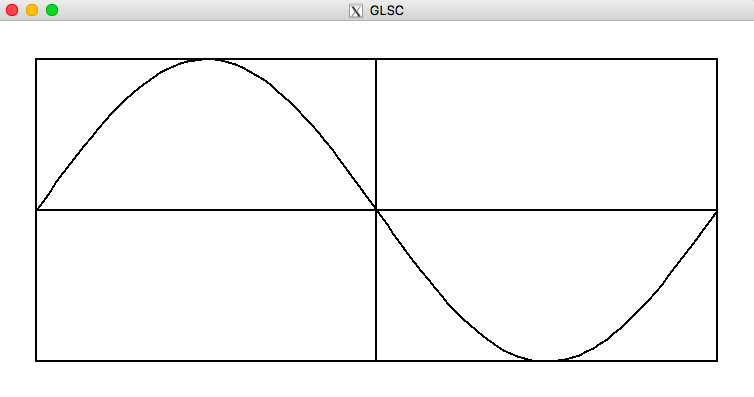
###完成図

##動的なsinカーブを描画
動的にするにはさほど上のプログラムを改変しなくても実現可能です。

move.c

#define T (10.0) //新しく定数を用意。
int main(){
  int k;
  dt = T/(N - 1);//Tが小さければ小さいほど動きは遅くなります。
  for(k=0;k<N;k++){
    //ここに先ほどのプログラムのg_sel_scaleからg_data_plotまでを記述。但し、
    //Y[i]=sin(i*dx + k*dt);に改変。
    //加えて最後の行にg_sleep(0.05);を追加
    //0.05秒間止まる
  }
}

完成したプログラムがこれ↓。

sin_curve_move.c

#include <glsc.h>
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#define N (100)
#define T (10.0)
#define L (2 * M_PI)

int main(){
  double dx,dt,Y[N];
  int i,k;
  //dxを計算
  dx = L/(N - 1);
  dt = T/(N - 1);
  //メイン関数内に描画画面の初期設定を記述
  g_init("GRAPH", 200.0, 200.0); //("GRAPH",標準座標のX,標準座標のY)
  g_device(G_DISP);
  //仮想座標系の定義
  g_def_scale(1, 0.0, L, -1.0, 1.0, 10.0, 10.0, 180.0, 80.0);
  g_def_scale(2, 0.0, L, -1.0, 1.0, 10.0, 110.0, 180.0, 80.0);
  for(k=0;k<N;k++){
    g_sel_scale(1);
    g_area_color(G_WHITE);
    g_line_color(G_BLACK);
    g_line_width(2);
    g_box(0.0, L, -1.0, 1.0, G_YES, G_YES);
    //x軸
    g_move(0.0, 0.0);
    g_plot(L, 0.0);

    //y軸
    g_move(L/2.0, 1.0);
    g_plot(L/2.0, -1.0);
    for(i = 0; i < N; i++){
        Y[i] = sin(i*dx+k*dt);
    }
    g_data_plot(0.0, L, Y, N);
    g_sleep(0.1);
  }
  g_sleep(G_STOP);
  g_term();
  return 0;
}

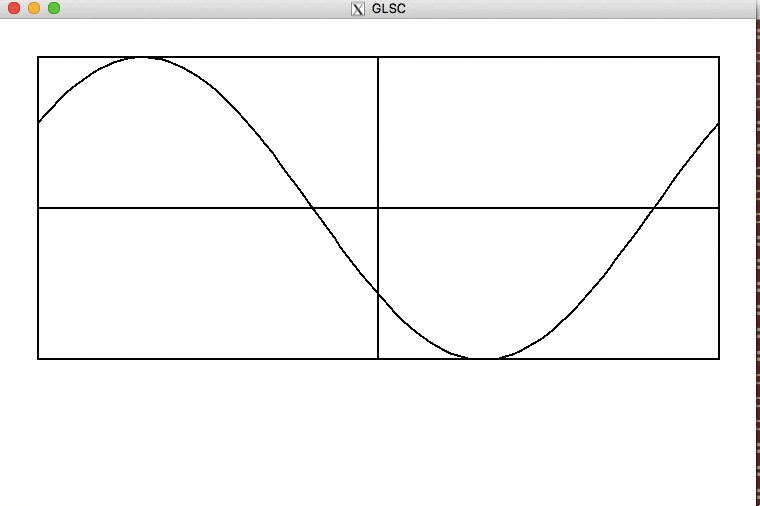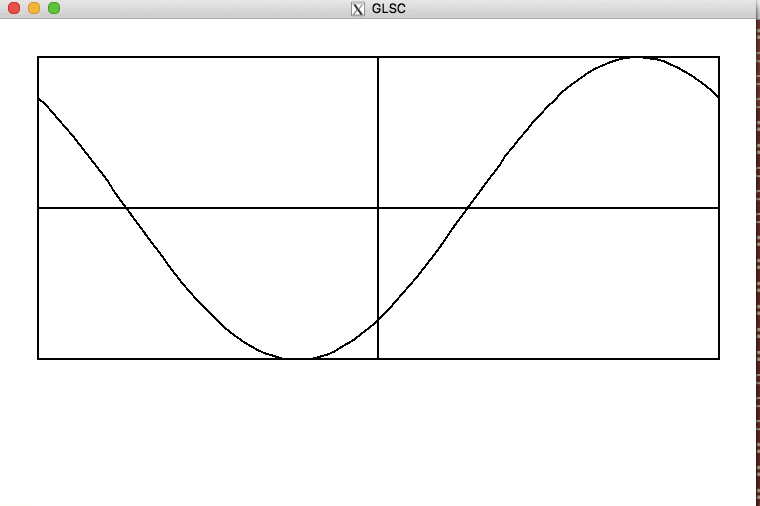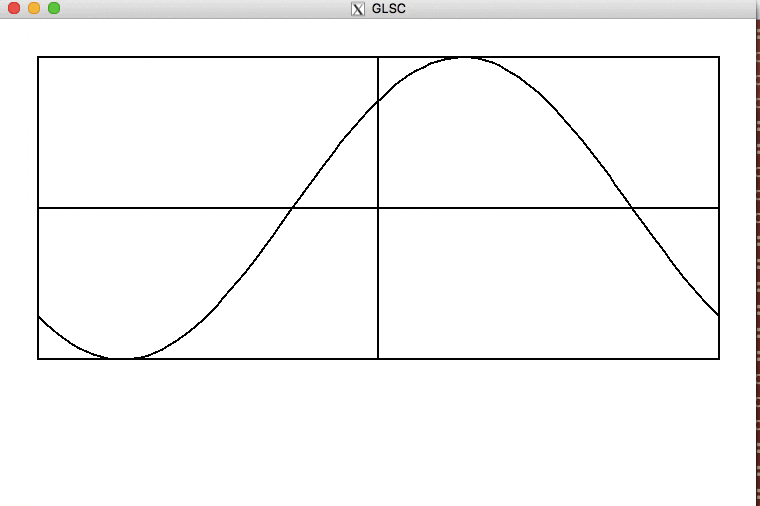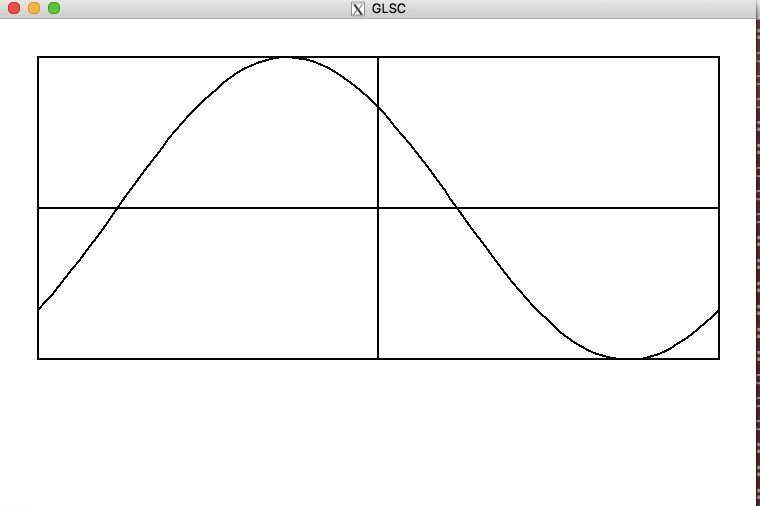
###完成図

#終わりに
今回はmathライブラリを用いてSinカーブを描画しましたが、それ以外にも様々なものが描画することができます。例えば乱数を用いてランダムな動きをシミュレーションすることも可能です。
GLSCは正直なところマイナーで、検索してもヒットするページがあまりないというところが現状なので初学者にとってはかなり辛い状況だと思います。少しでも役に立てればと思って今回記事を書きました。何か不明瞭なところがありましたら編集リクエストをお願いします。