LoginSignup
23
15

More than 5 years have passed since last update.

@jabberwocky0139

Pythonで覗く, こわくない量子力学3 : トンネル現象

Last updated at Posted at 2017-11-19

対象

量子力学を授業で習った or 自習した人に適した内容かと思います. 理系の学部生あたりでしょうか. プログラミングが好きだと尚良し！ 量子力学をまったく知らない人向けの内容ではありませんので悪しからず...

あらまし

Pythonで覗く, こわくない量子力学1 : 無限井戸型ポテンシャル
Pythonで覗く, こわくない量子力学2 : 有限井戸型ポテンシャル

のつづきです. 今回は定常Schroedinger方程式から固有状態を求めるのではなく、時間依存Schroedinger方程式を用いてあるポテンシャルに波束を置いたときの動きを見ます. 着目するのは表題の通り、波動関数のトンネリングです.

時間依存Schroedinger方程式

みんな大好き、Schroedinger方程式の時間依存Verです:
$$
i\hbar\frac{\partial}{\partial t}\psi(x, t) = H\psi(x, t) \\
H = -\frac{\hbar^2}{2m}\frac{d^2}{dx^2} + V(x)
$$

簡単のため、もちろん一次元. 解くためにまず設定しなければいけないのは、ポテンシャル$V(x)$と波動関数の初期状態$\psi(x, 0)$です.

ポテンシャルと初期波束は次のようなものです:
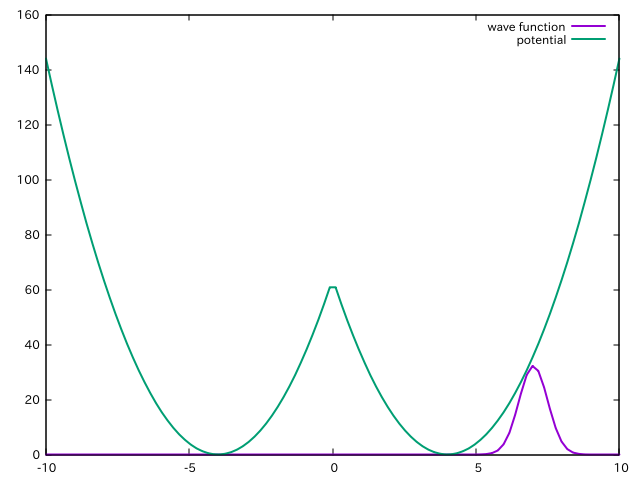
figure1.png

ポテンシャルはdouble-well型で、その片側に初期状態の波束をちょこんと置いてあげます.(具体的な関数は後述のコードを見てください)

古典描像であれば右側の井戸の中を行ったり来たりするだけですが、量子力学の世界ではさてどうなるでしょうか.

解法: Fourier変換

定常Schroedinger方程式ではないので、今回は固有値方程式ではなく多変数微分方程式です
今回も差分化で解いてあげてもよいのですが、せっかくなのでFourier変換を活用してあげましょう. 以前こちらの記事で拡散方程式をFourier変換で解いてあげました:
$$
\frac{\partial}{\partial t}f(x, t) = \frac{\partial^2}{\partial x^2}f(x, t)\\
\Rightarrow f(x, t) = {\cal F}^{-1}[e^{-k^2 t}{\cal F}[f(x, 0)]]
$$

${\cal F}$がFourier変換, ${\cal F}^{-1}$が逆Fourier変換にあたります. これをSchroedinger方程式に応用してあげましょう:
$$
i\frac{\partial}{\partial t}\psi(x, t) = \left(-\frac12\frac{\partial^2}{\partial x^2} + V(x)\right)\psi(x, t)\\
\Rightarrow \psi(x, t) = {\cal F}^{-1}[e^{ik^2 t}{\cal F}[e^{V(x)t}\psi(x, 0)]]
$$

$m$, $\hbar$は無次元化で1にしています. このFourier変換は時間⇔波数(エネルギー)の間に成り立つ変換です1. Fourier変換によって運動量項が演算子$e^{ik^2 t}$に、ポテンシャル項が$e^{V(x)t}$に化けたのがキモです. 元の式をちゃんと追うと、実は演算子まわりでちょっぴりゴマカシが入っていることがわかるのですが、トロッター分解という大義名分で正当化しています2. 少なくとも、普通に差分化するよりは遥かに良い方法であることが解析力学を駆使するとわかります3.

さて、この方法を用いてコーディングしていきましょう.

実装

コードの部分部分を順番に見ていきましょう

import

import os
import re
import numpy as np
from scipy.integrate import quad
from scipy.fftpack import fft
from scipy.fftpack import ifft
from scipy.fftpack import fftfreq
from inspect import getsource

numpy scipy は有り体に言ってFourier変換のためのimportです. os re inspect は何をするのかと言うと、、、あとで説明します.

関数定義

# --*-- Set functions --*--

# Set potential
# Note1 : Active line must be attached semicolon(;) at the end of line
# Note2 : Use the math function which work on gnuplot as well without any change
def Potential(x):
    #return x**2
    return 4*(x**2 - 8*abs(x) + 16);

# Potential on exp
def V(x):
    return -0.5j*Potential(x)

# Initial function
def Psi_0(x):
    y = lambda z: np.exp(-2*(z-7)**2)
    return y(x)/quad(y, -np.inf, np.inf)[0]/2

# file writer
def file_writer(filename, arr_func):
    with open(filename, "w") as f:
        for n, x in enumerate(np.linspace(-L/2, L/2, N)):
            print("{0}\t{1}".format(x, abs(arr_func[n])), file=f)

ポテンシャル($V(x)$は時間発展のための準備)と初期波動関数、ファイル出力のための関数たちです. あとで動画をしたためたいので、波束のデータをファイルに保存します4.

変数定義

# --*-- Set constants and variables for initial condition --*--

# Space step, Volume, Time step
N, L = 512, 25.0

# Maximum time, Time step number
tMax, tN = 20, 1024
dt = tMax/tN

# Set x-space
x = np.linspace(-L/2, L/2, N)

# Set expK, expV, initial function
expK = np.exp(-0.5j*(2*np.pi*fftfreq(N, d=1/N)/L)**2*dt)
expV = np.exp(V(x)*dt)
arr_Psi = Psi_0(x)

空間のサイズと分割数5、時間の刻みを設定します. さらに時間発展演算子$e^{ik^2 \Delta t}$、$e^{V(x)\Delta t}$を準備します. 本質的に時間の差分化をしていないので、$\Delta t$を細かくしなければ数値計算誤差が大きくなる、、、みたいな制約は全くありません.すばらしい.fftfreqが何者かはこちらのFourier変換の節を参照のこと.

時間発展

# --*-- Time propagation by symplectic numerical solution --*--

# Maximum file number
total_file = 200
# Output interval
interval = tN//total_file

# Time propagation
for i in range(tN):
    # output time depend function
    if(i%interval == 0):
        file_writer("output{0}.txt".format(i//interval), arr_Psi)

    # Multipling by time propagator of potential term
    arr_Psi = arr_Psi*expV

    # Fourier transformation
    arr_Psi = fft(arr_Psi)

    # Multipling time propagator of kinetic term
    arr_Psi *= expK

    # Inverse fourier transformation
    arr_Psi = ifft(arr_Psi)

このコードのキモにあたりますが、非常にシンプルです. 波束に$e^{V(x)\Delta t}$を掛けてFourier変換、その後$e^{ik^2 \Delta t}$を掛けて逆Fourier変換. 以上！

$$
\psi(x, t) = {\cal F}^{-1}[e^{ik^2 t}{\cal F}[e^{V(x)t}\psi(x, 0)]]
$$

コレをそのままコードに落としただけです. 今回は動画にするために$\Delta t$ずつ時間発展させています.

動画

# --*-- Gnuplot --*--

# Get provisional potential function as string
pattern = re.compile("(return.+;)")
m = pattern.search(getsource(Potential))
str_potential = "1.0/150*" + str(m.group(0))[7:-1]

# System call for gnuplot
gnuplot_call = 'gnuplot -e '
start = '"'
set_range = 'set xr[{0}:{1}]; set yr[{2}:{3}]; '.format(-L/2, L/2, 0, 0.5)
plot_initial = 'plot \\"output0.txt\\" w l lw 2 title \\"t = 0\\",{0} title \\"potential\\" w l lw 2; pause 2; '.format(str_potential)
do_for_declaration = 'do for[i = {0}:{1}:1]'.format(1, total_file-1)
do_for_start = "{"
do_for_procedure = 'plot sprintf(\\"output%d.txt\\", i) title sprintf(\\"t = %d\\", i) w l lw 2, {0} title \\"potential\\" w l lw 2; pause 0.05;'.format(str_potential)
end = '}"'

os.system("".join([gnuplot_call, start, set_range, plot_initial, do_for_declaration, do_for_start, do_for_procedure, end]))

os.system("rm output*.txt")

最後はGnuplotで動画をつくります. matplotlibでもいいんですが, なかなか動画を作るのが面倒なので. os.system()でshellが呼べることを利用してGnuplotを直接呼んでます. rangeの変数とかdo forのレンジとかはformat文で指定してます. この辺はPython埋め込みが便利なところで, もしpltファイルを別に用意したら, Lなりtotal_fileなりが変わったときに,pltファイルの方も修正しなければならないのがとても面倒です.

同様の理由からポテンシャルの関数も自動で参照してほしい. というわけでinspect.getsource()を使ってPotential(x)のソースコードを取得しています. そこから正規表現を用いてreturnから;までの部分を切り取ってあげてます. 

str_potential = str(m.group(0))[7:-1]

はreturnと;を切り取るようなスライスです. これでstr_potentialにはポテンシャル関数がstringで格納されました. ちなみに今回はポテンシャルを視覚的に手頃なスケールに変換して表示してます6.

出力ファイルを沢山生成しているので最後に

os.system("rm output*.txt")

で全削除. 1ファイルだけにまとめることもできますが, そうするとファイルサイズが大きくなりすぎてGnuplotの読み込みが遅くなります. 動画を作るときはファイルは分割したほうが良いみたいです.

ただ見ての通り、シンプルなコードとは程遠いです、、、ほんとはmatplotlibでやったほうがいいんでしょうけどね、、、

結果

波束がトンネリングして左の井戸に漏れ出しているのがわかります. 古典描像に慣れているとなんとも不思議ですよね. みんな大好きトンネル現象も、思ったよりかんたんに書けてしまいます. そう、Pythonならね

  1. それとは別に、位置⇔運動量の間で成り立つFourier変換もあります. 一般的にFourier変換とは共役な変数の間で常に成立する変換です.  ↩

  2. コメントでご指摘頂きましたが、これはトロッター分解の1次近似の形式になります(トロッター分解はTaylor展開の演算子版みたいなやつです). 2次以上を取り入れることで更に精度を上げることができますが、正直1次でも十分な精度です. ↩

  3. この方法はSymplectic数値積分法と呼ばれており、いくら時間発展をブン回してもエネルギーが保存されることが保証されています. 差分法だと時間発展に従ってエネルギーが発散したり減少したりと、けっこう嫌なことがまま起こります.  ↩

  4. print関数でもファイル保存できるんですよー ↩

  5. 時間は差分化しませんが、空間は差分化します. ↩

  6. そもそもポテンシャルと波動関数では縦軸の次元が違うのでそもそもスケールの議論はナンセンスな話です. ポテンシャルはエネルギー、波動関数は存在確率です. ↩

23
15
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
23
15