あらまし
四則演算から微分方程式, 最適化まで数値計算で扱えるモノは多岐に渡ります. 解析計算では非常にテクニカルなものでも, 数値計算に投げると非常に単純に事が済むことも多々あります. 例えば高校でやった(定)積分では, 置換積分・部分積分を駆使して多種多様な問題に対処してきましたが, 数値計算に投げればアルゴリズムはだいたいみんな一緒です. 微分方程式だって似たようなものです. 大規模な行列演算なんて手でやる人はいないでしょう.
初めて数値計算に触れた人はもれなく「もう手で解く必要ないんじゃね?」と思うかもしれません. 自分は思いました. でも「数値計算で解けるものは積極的にぶん投げよう!」が正解かというと, それもまた違う気がします. この記事では, マシンパワーに身を委ねきれない事柄についてまとめたいと思います.
コード例はPythonです.
0. 解析計算はできない
当たり前のことですが, 解析計算はできません. つまり関数の概形は描けても関数を直接求めることはできないということです. 数値微分・数値積分は値を出すだけで関数を求めているわけではありません. もちろんその値を用いてフィッティングすることは可能ですし, MathematicaやSymPyに投げることで解析計算をマシン上で実行することも可能ですが, それは数値計算とはまた別の話. また, 解析をしなければ定性的な議論も困難になります.
1. 特異点に弱い
数値計算では特異点が絡むものを扱うのが困難です. 例えばディラックデルタを含む定積分
$$
\int_{-\infty}^\infty dy\ f(y)\delta(x-y) = f(x)
$$
を数値的に計算することはできません. これは数値計算で無限大を扱うことができないことに起因します. 実は, ディラックデルタはおおよそ
$$
\delta(x) =
\begin{cases}
\infty\ \ (x = 0)\\
0\ \ (otherwise)
\end{cases}
$$
のような関数です. 一口に無限大と言ってもそれぞれに大小関係があり, そのような機微を数値で表現することもまた不可能です1. また, 引力系の力学では2体の接触が特異点になるため, 微分方程式も正確に解くのが困難です:
— Jabberwocky (@jabberw75864611) 2016年12月23日
画像と動画は差分の細かさを変えていますが, それが特異点による影響で軌道が変わっています. しかし, この手の特異点はうまいことやって回避することが可能です. 微分方程式は難しいので, 積分で例えてみましょう.
回避方法
とある積分
$$
\int_0^1 dx \frac{f(x)}{\sqrt{1 - x^2}}
$$
も, 被積分関数が積分区間に特異点($x = 1$)を含んでいます. しかし, $1-x = t^2$ という変換を施すと
$$
2\int_0^1 dt \frac{f(1-t^2)}{\sqrt{2 - t^2}}
$$
のように特異点の回避が可能です. コードに落とすとこんなかんじ2:
import math as m
from scipy.integrate import quad
N, L = 100, 1
dx = L / N
eps = 1e-5
x_arr = np.linspace(0 + eps, 1 - eps, N)
def integrate(g=lambda x: m.sqrt(1 - x**2), h=lambda x: x):
ans = 0
for i in x_arr:
ans += h(i)**2 / g(i) * dx
return ans
print("before: {0}".format(integrate()))
print("after: {0}".format(integrate(g=lambda x: 0.5 * m.sqrt(2-x**2),
h=lambda x: 1-x**2)))
print("correct: {0}".format(quad(lambda x: x**2 / m.sqrt(1 - x**2), 0, 1)[0]))
>>> before: 2.911010886201887
>>> after: 0.7846167974746113
>>> correct: 0.7853981633974282
$f(x) = x^2$です. 特異点があると随分ズレますね. でも回避してあげれば単純な区分求積でも, SciPyで計算したものと遜色ありません.
2. 数値誤差の累積
PCで扱うのは基本的に有限ビットの浮動小数点であるので, 誤差が出るのは必然です. もちろん性質の良い関数などを扱う上で問題になることはないです. ではタチの悪い関数ではどうでしょう?
$$
Z_{ml}(z) \equiv \frac{1}{(m-l)!}\sqrt{\frac{m!}{l!}}z^{m-l}e^{-\frac14 z^2}
$$
これは$l, m$がある程度の値を持つ領域では, 発散する部分と0に収束する部分の積が常識的な値になるという構造を持っています. いわゆる$0 \times \infty$の不定形ですが, この繊細な構造を持った関数を数値計算にそのまま投げると, floatの誤差で死にます. が, 実はこれも式変形で救えます.
回避方法
$$
Z_{ml} = \frac{\sqrt{_m P_{m-l}}}{(m-l)!}z^{m-l}\left(e^{-\frac{z^2}{4(m-l)}}\right)^{m-l} = \prod_{k=0}^{m-l-1}\left[\frac{\sqrt{m-k}}{m-l-k}ze^{-\frac{z^2}{4(m-l)}}\right]
$$
階乗と指数関数を細かく刻んだわけですが, ひとつひとつの項は(恐らく)常識的な値に落ち着いているので, 誤差による発散がある程度抑えられています:
import math
def Z(m, l, z):
fact = math.sqrt(math.factorial(m) / math.factorial(l)) / math.factorial(m - l)
exp = z**(m - l) * math.exp(-0.25 * z**2)
return fact * exp
def Z_modified(m, l, z):
ans = 1
for k in range(m - l):
ans *= (m - k)**0.5 / (m - l - k) * z * math.exp(-0.25 * z**2 / (m - l))
return ans
m, l, z = 300, 70, 6.9
print(Z_modified(m, l, z))
print(Z(m, l, z))
>>> 1.2023119157807856
>>> OverflowError
$m = 300,\ l = 70,\ z = 6.9$のとき実際には$1.2$程度ですが, 手を加えないとオーバーフローです.
解析計算は数値計算の彼岸ではない
連続を扱うことができるか否かという点から数値計算と解析計算は相反する概念のように思っていましたが, 必ずしもそうではありません. ということで, 解析計算(式変形)によって数値計算の不具合を解消する例を挙げてみました. 差分化を極限まで細かくしていけば無限の問題もある程度回避はできますが, 実行時間はマシンパワーに強く依存します. そのマシンパワーを解析計算がものすごい精度を持って肩代わりするわけです. 非線形微分方程式は解析的に解けませんが, これは解析計算の敗北というよりは数値計算の裏方にまわったようなものなのです.
結局何が言いたいかといえば, 解析的に解けないものがどれだけあろうとも, マシンがどれだけ高速化しようとも, 解析計算の価値は揺るがないということです. 連続を扱えるという点に於いても, マシンの裏方になれるという点に於いても. 数学, がんばりましょう.
こぼれ話: 哀愁のニューラルネット
ニューラルネット話ですが, 自分は専門でないどころかかなりの不勉強です. アホなこと言ってる箇所がいくつかあるはずです. 優しく流し目でスルーして頂くか, コメントで突っ込みを入れて頂けると嬉しいです.
これまで解析計算がいかに重要かを主張してきたのですが, 逆にマシンパワーをぶん回す方面に特化した分野があります. ニューラルネットワークです.
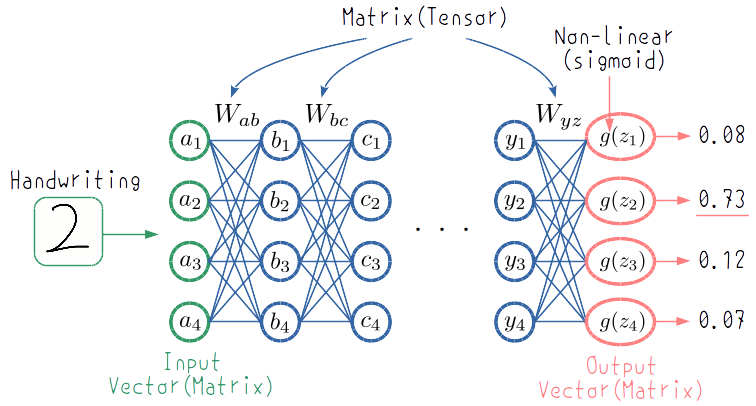
例えば数字を認識するネットワークがあったとしましょう.
ニューラルネットの仕組みについて解説している記事はたくさんあるので, ここでは特に細かくは書きません. 上の図では手書き画像の「2」をベクトルとして入力し, 各層ごとに線形変換をガスガスかけています. 最後の出力段で2番目の値が最も大きいことからネットワークが「これは2だ!」と認識しています. 仕組み自体は非常に単純です.
このように数字を認識できるようなネットワークに仕立てあげる(学習させる)ために各行列の要素を弄っていくことになるのですが, それを弄る指標となるのが評価関数です. 評価関数を最小にするように行列要素を弄っていくことになるのです. 最適化問題です. 例えば評価関数が以下のようなものだったとします:
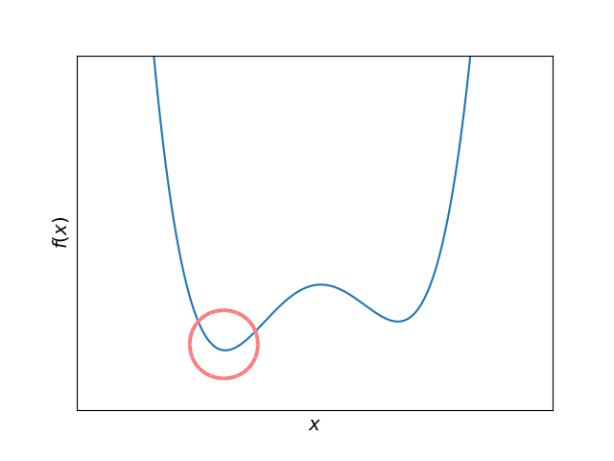
横軸が行列要素だと思ってください. 左側の方に落ちればOK. これくらいなら最小点に落とすのはそんなに難しくなさそうですが...
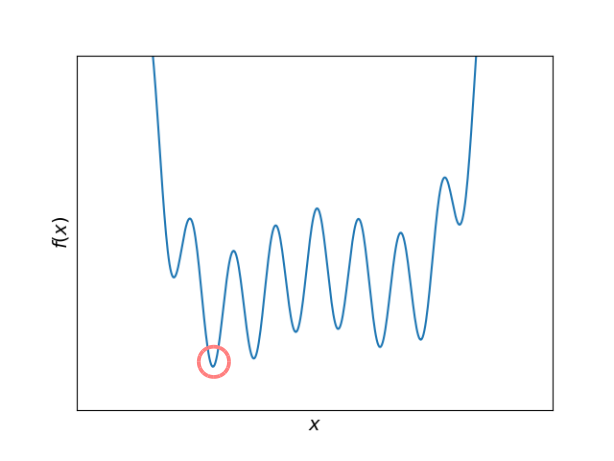
これくらいになるとちょっと厄介です. 単純なアルゴリズムでは極小に落とせても最小に落とすのは簡単ではありません. しかも, これは一次元の最も単純な例です. 本来, 行列要素は膨大な数に及ぶはずで, もし100個あれば100次元です. ヤバイ. とても手に負えなさそうなモデルですが, これをGPGPUで乗り切ろうとするのがトレンドのようです. レベルを上げて物理で殴れ.
もちろん様々なアイデアや数学なども駆使してはいるでしょう. しかし, もともとのモデルが非常に単純であるが故に自由度が大きすぎるため, その自由度を上手く制御するためのアイデア・数学は難解になる傾向があるような気がします3. 逆にモデル自体がある程度の複雑さを持っている場合は, それを制御するテクニックはそこまで高度になりづらい気がします. そりゃそうだ. そうでなきゃモデルを複雑にする理由がないですよね.
非常に流行っている分野なので進歩のスピードも速いですが, モデルの中に解析計算が割り込む余地が少ない4ために, 定性的な理解が難しいように思います. 特にネットワークの出す結論がどのような過程を経て出されたものなのかを理解するのは困難っぽいです. マシンパワーに身を委ねすぎて人間が思考停止しているような気がしてきます5. しょんぼり.
しかしそんなことを言ってられないほどニューラルネット・ディープラーニングの流行はもの凄いです. 自分もアホなこと言ってないで勉強しなきゃいけないですね.