あらまし
Couseraの機械学習コースをはじめました.前々から視界にはかすめていたのですが、やっと今頃重い腰を上げた次第です.しかし、Octaveで書くのが少々億劫1だったこと、コードの一部を埋めるのではなくインターフェイスから全て自分で書いたほうが勉強になると思い、Pythonで書き直してみることにしました.この記事は自分の勉強メモです.
一応Courseraを受講していない人でもなんとか追えるかな?という内容にしたつもりです.もし興味を持たれたら、ぜひ受講してみてください.最高に丁寧ですばらしい講義ですよ.
巷に溢れる機械学習の教材のひとつとして、利用して頂けると幸いです.
機械学習のキモ
機械学習で登場する重要キャラクターの紹介です.5人います:
① $X$: 入力データセット.例えば 1.土地の広さとか、 2.タイタニック号乗船者の性別・年齢とかとか
② $y$: 出力データセット.例えば 1.に対する価格とか、 2.に対する生還可否とか.
これが「教師」にあたります.この入力$X$に対して出力$y$を返すような関数を見つけることが機械学習の主目的です.
③ $h_{\theta}$: 仮説(hypothesis)関数.$h_{\theta}(X) \simeq y$ となるような$h$を見つけたい.そうすれば、土地の広さに対する価格を予測できたり、タイタニック号に乗るか否かの判断を理知的に下すことができる.すごい
機械学習はその名の通り、データセットを使って$h_{\theta}(X)\simeq y$を満たすように$h_{\theta}$鍛えていきます.勉強なら脳みそ、運動なら筋肉、パラメータ$\theta$こそが機械学習における脳みそ・筋肉です
④ $\theta$: 仮説関数に含まれるパラメータ.この$\theta$を弄って、$h_{\theta}(X) \simeq y$を実現したい.
ではどのようにして$\theta$を決定するか.そのアイデアはシンプルです.$h_{\theta}(X) = y$からのズレを定量化してそのズレを最小化するような$\theta$を見つければよいのです. ズレが少なければ$h_{\theta}(X) \simeq y$としてよかろう、ということです.そのズレをコスト関数と呼びます
⑤ $J(\theta)$: コスト関数.$X, y, \theta$を使った理想からズレとして定義されます.これを最小化していく過程を「学習」と呼びます.
以上が概略になります.これだけだと、そんなに難しくなさそうですね.機械学習におけるモデルとは
- 仮説関数をどのように定義するか
- コスト関数をどのように定義するか
の2点に集約されます.$J(\theta)$を最小化するのは単なる数学(最適化問題)です.その手のことはPython様はお手の物です.
**この5キャラクターについてはしっかり覚えておいてください.**彼らを中心にストーリは進んでいきます.
1. 線形回帰
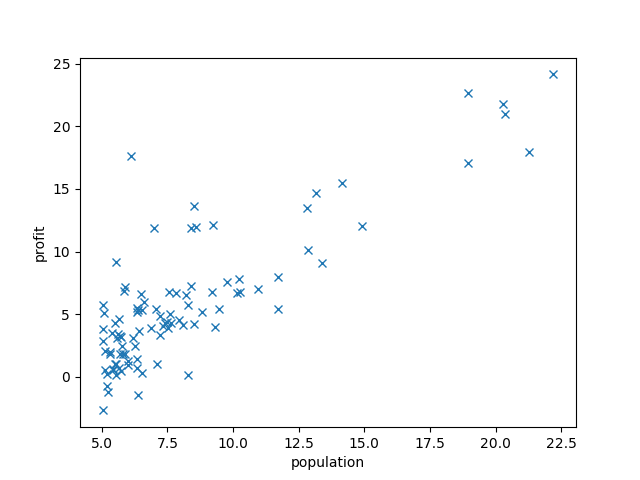
横軸が都市の人口、縦軸がその都市にあるレストランの売上です.横軸が$X$、縦軸が$y$に相当します2.都市の人口を入力したらレストランの売上を吐き出す関数$h_\theta$を求めていきましょう.ひとまず、$h_\theta$がどんな関数になるかを考えてみましょう:
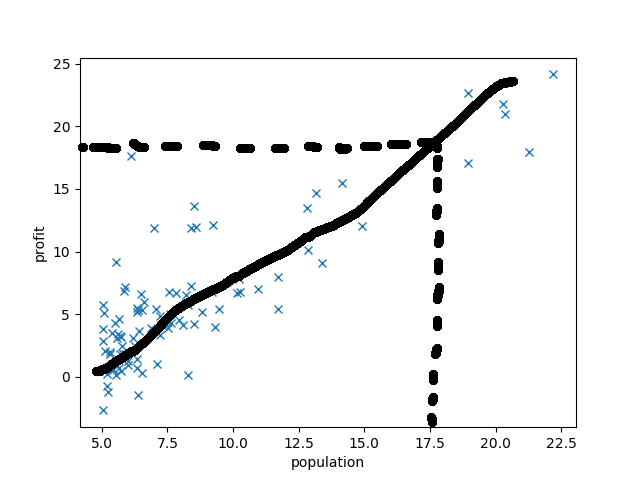
だいたいこんなかんじでしょうか.$h_\theta$を直線と仮定してあげるのがよさそうですね.$h_\theta(17.5) = 18$てなもんでしょう(雑).
入力$X$を引数に取り、$\theta$を含み、線形関数となれば自ずと形は決まってきますね:
$$
h_\theta(X) = \Theta^T X = \theta_0 + \theta_1 x_1\\
X = (x_0, x_1) = (1, x_1)\\
\Theta = (\theta_0, \theta_1)
$$
このモデルにおける筋肉は、直線の傾きと切片なわけですね.
次にコスト関数を定義しましょう.コスト関数とは理想とのズレです
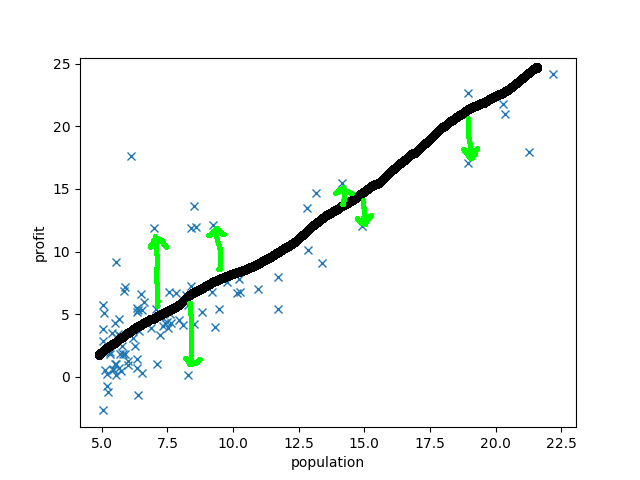
いくつかの点について誤差を緑矢印で示しました.**この誤差を全ての点について取ってあげて足し合わせればコスト関数の出来上がりです.**ただし、上側にズレてても下側にズレてても等価なので、符号を打ち消すために2乗してあげましょう:
$$
J(\theta) = \frac{1}{2m} \sum (h(x^{(i)} - y^{(i)})^2
$$
$m$はデータセットの数です. 平均を取ることに大きな意味はありませんし、さらに1/2することにも計算上の理由でしかありません.大事なのは$\sum$以降です.これを最小化してあげればトレーニング完了です.めでたし
ただの最小2乗法じゃないか!と思った方、そのとおりです.でもこれこそ、最もシンプルで機械学習のエッセンスを学べる題材なのでしょう.
$J(\theta)$の最小化はSciPy.optimizeとかに投げてしまえば終わりですが、講義の方では最急降下法を用いています.$J(\theta)$の傾きを求めて、坂を下っていくようなアルゴリズムです:
$$
\frac{\partial J}{\partial \theta} = \frac{1}{m}\sum_j (h{x^{(i)}} - y^{(i)})x_j^{(i)}
$$
適当な重み$\alpha$を掛けて$J(\theta)$が小さくなる方へ徐々に転がっていくようにしてあげましょう:
$$
\theta_j = \theta_j - \frac{\alpha}{m}\sum_j (h{x^{(i)}} - y^{(i)})x_j^{(i)}
$$
今回はこのアルゴリズムを採用してコードに落としていきます.
実装
まずは入出力データを取り込みます:
import numpy as np
import matplotlib.pyplot as plt
class Ex1Data(object):
def __init__(self, filename):
self.x = []
self.y = []
self.alpha = 0.01
self.filename = filename
def input_data(self):
with open(self.filename, 'r') as f:
for line in f.readlines():
a, b = line.split(',')
self.x.append(float(a))
self.y.append(float(b))
self.x = np.array(self.x) # numpyに変換
self.y = np.array(self.y) # numpyに変換
self.m = len(self.x)
self.X = np.hstack((np.ones((self.m, 1)),
np.reshape(self.x, (self.m, 1))))
def plot_data(self, theta):
plt.plot(self.x, self.y, 'x')
plt.xlabel('population')
plt.ylabel('profit')
plt.plot(self.x, theta[0] + theta[1]*self.x)
plt.show()
$X, y$をファイルから入力して、ついでにプロット用のメソッドもつけたクラスにしています. 特にヒネりはありませんが、$X = (x_0, x_1) = (1, x_1)$という形式の入力を想定している(ファイルから入力されるデータは$X$ではなく$x_1$)ので、np.hstackで$x_0 = 1$を追加しています.
ではこの入力をもって、仮説関数・コスト関数を定義してトレーニングするためのクラスをつくります:
class CostFunction(object):
def __init__(self, data):
self.data = data
self.theta = np.array([0.0, 0.0]) # 初期値
self.J = None
def hypothesis(self):
return np.matmul(self.data.X, self.theta)
def compute_J(self):
h = self.hypothesis()
self.J = 0.5 * np.mean((h - self.data.y)**2)
return self.J
def compute_grad(self):
h = self.hypothesis()
self.theta -= self.data.alpha / self.data.m * np.matmul(h - self.data.y, self.data.X)
これもまあ、そのまんまですね.compute_gradを1回まわすと1ステップ分$J(\theta)$の坂道を下っていくイメージです.ではこれらをつなげて動かしてみましょう:
class Interface(object):
def __init__(self):
self.data = Ex1Data(filename='ex1data1.txt')
self.cost = CostFunction(self.data)
def compute(self):
# データ入力
self.data.input_data()
# コスト関数
print('cost before: {0}'.format(self.cost.compute_J()))
# 最急降下法
for _ in range(1500):
self.cost.compute_grad()
# コスト関数
print('cost after: {0}'.format(self.cost.compute_J()))
print('theta: {0}'.format(self.cost.theta))
self.data.plot_data(self.cost.theta)
if __name__ == '__main__':
hoge = Interface()
hoge.compute()
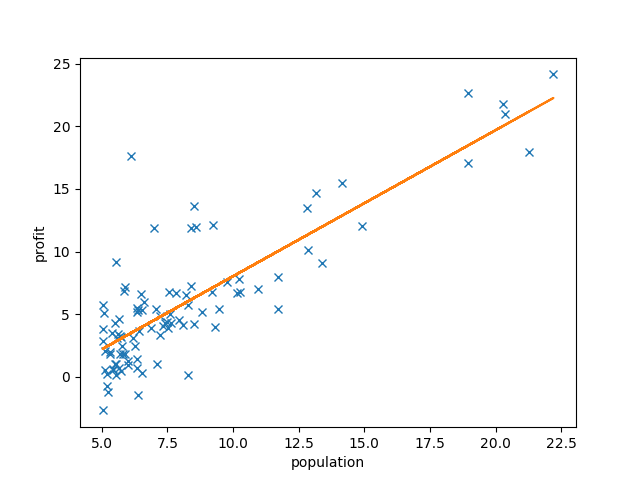
最急降下法を1500回ほど回しています. オレンジの線がトレーニング後の仮説関数です.かくして、都市の人口に対するレストランの売上を予言できるようになりました.
この程度なんてことないじゃないかと思われるかもしれません.でもそれは、入力が1系統しかなかったからです. タイタニックの例だと入力は「性別」「年齢」の2系統です.モノによっては入力がめちゃくちゃ多岐に渡るデータセットもあるでしょう.そうなると今回のようにグラフから直感的に理解することは難しくなります.そんな場合でも、$X, \theta$の次元を上げるだけで今回のモデルは簡単に流用可能なのです.すごい.
2. 分類: 基礎
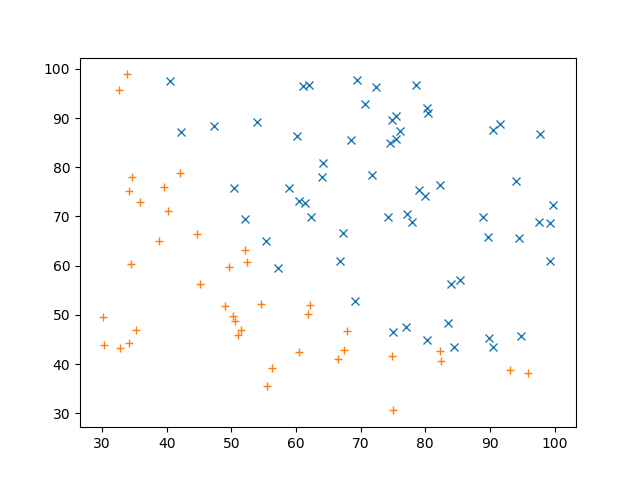
横軸がテスト1、縦軸がテスト2の点数だとして、青☓が合格/橙+が不合格です.入力データセット $X$が2つのテストの点数、出力データセット$y$は0(不合格)と1(合格)の2種類です.どっちのテストの成績も良ければもちろん合格なので右上に☓が多く、左下は+が多いですね.このデータでもって学習させて、2種類のテストの点数から合格不合格を予測してみましょう.まずざっくりどのように分類できるかというと
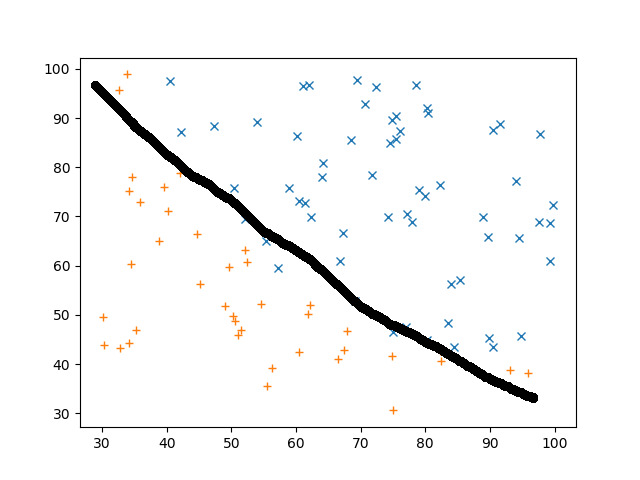
こんなもんでしょう.さて、モデルをどのように作りましょうか、、、まずは仮説関数です
$$
h_\theta (X) = \frac{1}{1 + e^{-\Theta^{T}X}}
$$
こうします.なんぞ!?って感じでしょうが、1次元の例で軽く説明します.上のグラフはこんなかんじです:
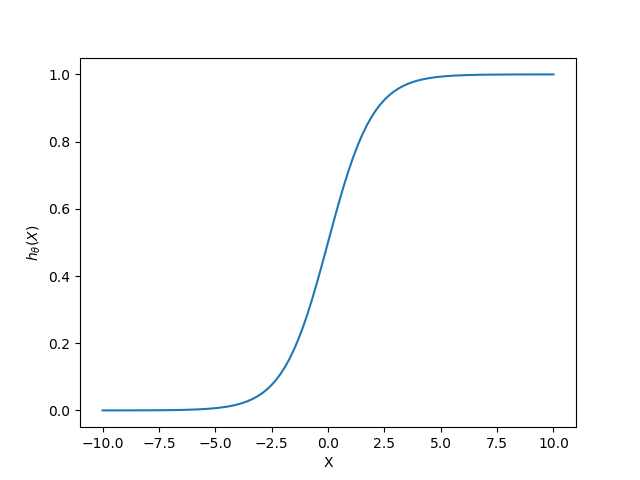
横軸がX、縦軸が仮説関数の出力です.図の右側は1に、左側は0に収束するような関数です.いわゆるシグモイド.
なんとなくわかるでしょうか?この関数は分類に使えそうですね.上の図の例でいけば、「$X>0$は合格、$X<0$は不合格」といった感じ.正確には「$h_\theta (X) > 0.5$ならば合格、$h_\theta (X) < 0.5$ならば不合格」となるでしょうか.$\theta$をトレーニングしてあげれば0→1が切り替わる位置をコントロールできそうですね.上の一次元の例ならば仮説関数は
$$
h_\theta (X) = \frac{1}{1 + e^{-\Theta^{T}X}} = \frac{1}{1 + e^{-(\theta_0 + \theta_1 x_1)}}
$$
ですね、2次元ならば
$$
h_\theta (X) = \frac{1}{1 + e^{-\Theta^{T}X}} = \frac{1}{1 + e^{-(\theta_0 + \theta_1 x_1 + \theta_2 x_2)}}
$$
などなど.実はもっと自由度の高い仮説関数を用意することもできますが、割愛.
さて、コスト関数はどうすればよいでしょうか?たとえば以下のようなデータセットで学習をするとしましょう
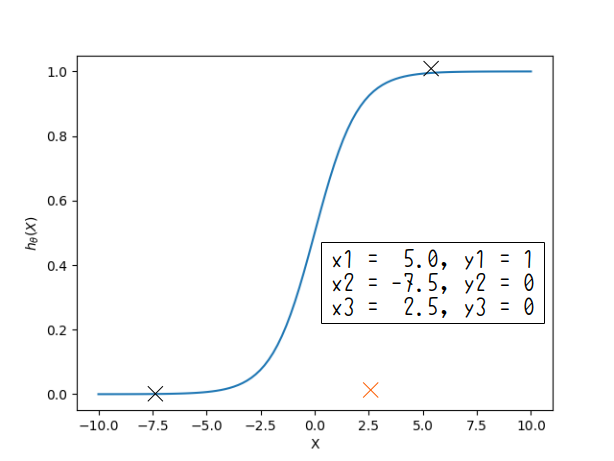
$(x_1, y_1)$, $(x_2, y_2)$はコスト関数と概ね一致していますが、$(x_3, y_3)$は仮説関数から外れたデータになっています.**こういう状態のとき、コスト関数は大きな値を取って欲しいわけです.**そのコスト関数を最小化した時、$h_\theta (x_3) \simeq y_3$となってくれるでしょう.ということで、コスト関数の種明かしです.
$$
J(\theta) = \frac{1}{m}\sum_j \left[-y_j^{(i)}\log(h_\theta (x_j^{(i)})) - (1-y_j^{(i)})\log(1-h_\theta (x^{(i)}_j ))\right]
$$
$\sum$以下の第一項は$y^{(i)}=1$のときに、第一項は$y^{(i)}=0$のときにのみ機能します.だって$y^{(i)}=1$のときは第二項は0ですからね.ではこのグラフがどうなっているかと言うと
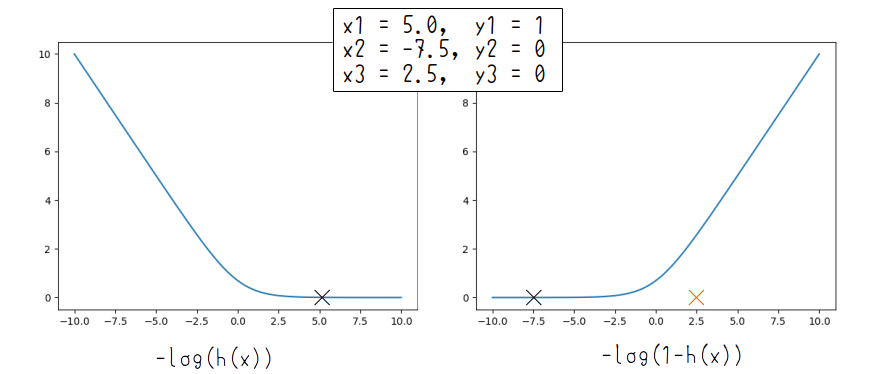
こんなかんじです.左が$y^{(i)}=1$のとき、右が$y^{(i)}=0$のときです.$x_3=2.5, y_3=0$があるおかげでコスト関数が大きくなるメカニズムがこれで解ると思います.
駆け足ですが、これをコードに落としていきましょう.ちなみに今回扱うものは2次元なので、仮説関数はこんな感じになります:
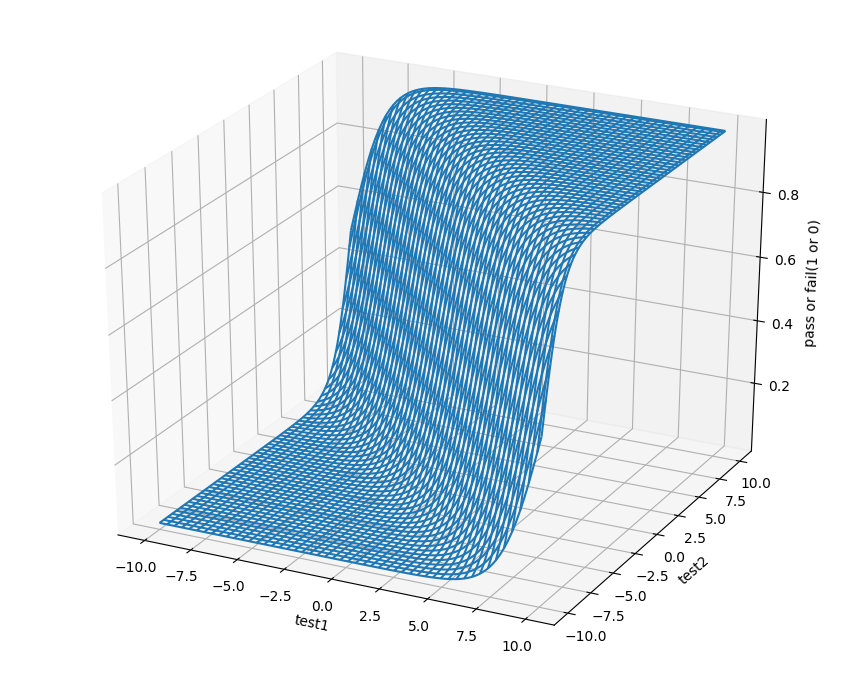
滝みたいなかんじですね.
実装
まずはデータの入力:
import numpy as np
from scipy.optimize import fmin_cg
import matplotlib.pyplot as plt
class Ex2Data(object):
def __init__(self, filename):
self.X = []
self.y = []
self.m = None
self.filename = filename
def input_data(self):
raw_data = np.loadtxt(self.filename, delimiter=',') # numpyに直接格納
self.y = raw_data[:, 2]
self.m = len(self.y)
self.X = raw_data[:, :2]
self.X = np.column_stack((np.ones(self.m), self.X))
def plot_data(self, theta):
X1 = self.X[self.y == 1]
X2 = self.X[self.y == 0]
plt.plot(X1[:, 1], X1[:, 2], 'x')
plt.plot(X2[:, 1], X2[:, 2], '+')
plt.plot(self.X[:, 1], - (theta[0] + theta[1] * self.X[:, 1]) / theta[2]) # リニア
plt.show()
これは前回とほぼ同じですが、一点注意.合格不合格の境目をこれから図示していくのですが、境目の定義は$h_\theta (X) = 0.5$でした.つまり境界線は
$$
h_\theta (X) = \frac{1}{1 + e^{-\Theta^T X}} = \frac{1}{1 + e^{-(\theta_0 + \theta_1 x_1 + \theta_2 x_2 )}} = 0.5\\
e^{-(\theta_0 + \theta_1 x_1 + \theta_2 x_2 )} = 1\\
\theta_0 + \theta_1 x_1 + \theta_2 x_2 = 0\\
x_2 = -\frac{\theta_0 + \theta_1 x_1}{\theta_2}
$$
となるのです.これをプロットするコードをplot_dataに追加しています.
では次に仮説関数、コスト関数を定義してトレーニングです:
class CostFunction(object):
def __init__(self, data):
self.data = data
self.theta = np.array([-24, 0.2, 0.2]) # 初期値
self.J = None
def sigmoid(self, z):
return (1 + np.exp(-z))**-1
def hypothesis(self, theta):
return self.sigmoid(np.matmul(self.data.X, theta))
def compute_J(self, theta):
h = self.hypothesis(theta)
y = self.data.y
self.J = np.mean(-y * np.log(h) - (1 - y) * np.log(1 - h))
return self.J
def optimize_theta(self):
self.theta = fmin_cg(self.compute_J, self.theta, maxiter=1000)
これも前回のコードと構造は同じです.ただ今回はコスト関数$J(\theta)$の最小化にscipy.optimize.fmin_cgを使っています.最急降下法の上位互換みたいなアルゴリズムです.
では組み合わせて動かしてみましょう:
class Interface(object):
def __init__(self):
self.data = Ex2Data(filename='ex2data1.txt')
self.cost = CostFunction(self.data)
def compute(self):
# データ入力
self.data.input_data()
# 最小値問題
self.cost.optimize_theta()
# コスト関数
print('cost after: {0}'.format(self.cost.compute_J(self.cost.theta)))
print('theta: {0}'.format(self.cost.theta))
self.data.plot_data(self.cost.theta)
if __name__ == '__main__':
hoge = Interface()
hoge.compute()
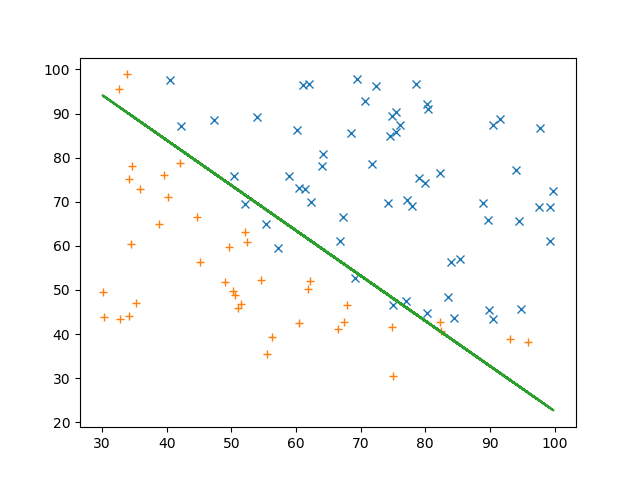
めでたし!今回は仮説関数がシンプルなので境界線が直線ですが、もっと複雑な仮説関数を用意すれば曲線にすることもできます.
3. 分類: 文字認識
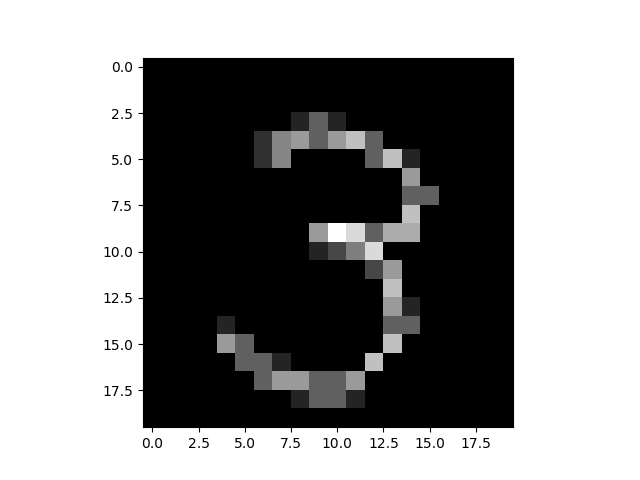
前回は分類するものが2種類しかありませんでしたが、2個以上のものを分類するにはどうすればいいでしょうか?わかりやすい例が手書き数字認識です:
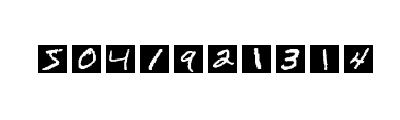
10種類の分類問題になります.さてどうしましょうか?前回の例では出力が$y = 0, 1$の2パターンしかないことを利用してコスト関数を定義しました.今回の出力データセットは$y = 0, 1, 2, ... , 9$なので、これを真に受けると前回のコスト関数は使えません、、、
ではどうするかと言うと、$y$を10パターンに増やすのではなく、$\Theta$を10パターンに増やしてしまいましょう.つまり$\Theta_0$は、入力が0か否かを判定するためのパラメータ、$\Theta_1$は入力が1か否かを判定するためのパラメータ、...$\Theta_9$は入力が9か否かを判定するためのパラメータ、と定義するのです.入力を10パターンの仮説関数$h_{\theta_n}$に通して、$h_{\theta_n} > 0.5$となった項目が判定した数字になります.というわけで、トレーニングは10パターン行うことになるのです.
上のアイデアを踏まえれば、やることは前回のコードとほぼ同じです!
実装
まずはデータの入力です:
import scipy.io as spio
from scipy.optimize import fmin_cg
import matplotlib.pyplot as plt
import numpy as np
from random import gauss
from itertools import cycle
Lambda = 0.1
eps = 1e-10
iter_label = cycle([10] + [i for i in range(1, 10)]) # 10, 1, 2, 3,..., 9, 10, 1, 2,...
class Data(object):
def __init__(self):
self.X = None # トレーニングデータ
self.label_num = 10 # ラベル数
self.X_num = [None for _ in range(self.label_num)] # ラベルごとのトレーニングデータ
self.y = None # 出力期待値
self.theta = np.array([None]*self.label_num) # 学習パラメータ(0-9の10パターン)
def input_data(self, filename):
mat = spio.loadmat(filename)
self.X, self.y = np.array(mat['X']), np.array(mat['y'])
m, n = self.X.shape
self.X = np.column_stack((np.ones(m), self.X))
self.theta = np.array([[gauss(0, 0.1)] * (n + 1) for _ in range(10)],dtype=float)
for i in range(self.label_num):
self.X_num[i] = self.X[self.y.T[0] == next(iter_label)]
return self.X, self.y, self.theta
def plot_data(self, X, label=0):
plt.imshow(X[label][1:].reshape(20, 20).T, 'gray', vmin=0, vmax=1.0)
plt.show()
入力データは20x20のピクセル値を一次元に直したものです.今回の例題では手書き数字0に対する出力は$y = 10$となっています.0以外の数字は出力と一致しています.前回と異なるのは$\Theta$が10パターンあることです.
あと今回は少々$\theta$の初期に敏感になります.全部0に初期化するとどうも上手く動かなかったため、適当に乱数で与えています.最適化のアルゴリズムを変えると初期値依存も変わりそうです.
ではトレーニングのクラスです:
class Calc(object):
def __init__(self, X, y, theta):
self.X = X
self.y = y
self.theta = theta
self.m = self.X.shape[0]
def _sigmoid(self, z):
return (1 + np.exp(-z))**-1
def hypothesis(self, theta, X):
return self._sigmoid(np.matmul(X, theta))
def _cost(self, theta, *args):
X, y, label = args
h = self.hypothesis(theta, X)
y = np.array(y == label, dtype=float).reshape(1, self.m)[0]
J = np.mean(-y * np.log(h + eps) - (1 - y) * np.log(1 - h + eps)) + Lambda / (2 * self.m) * np.sum(theta ** 2)
return J
def _gradient(self, theta, *args):
X, y, label = args
h = self._sigmoid(np.matmul(X, theta))
y = np.array(y == label, dtype=float).reshape(1, self.m)[0]
tmp_theta, theta[0] = theta[0], 0.0
grad = np.matmul((h - y), X) / self.m + Lambda / self.m * theta
theta[0] = tmp_theta
return grad
def optimize_theta(self, theta, label):
theta = fmin_cg(f=self._cost, x0=theta, args=(self.X, self.y, label), fprime=self._gradient)
return theta
10種類のトレーニングを行うために前回からいくつかコードを足しています.
① 例えば3を分類するトレーニングを行うときは、出力の$y = (10, 1, 2, 3, 4, 5, 6, 7, 8, 9)$を$y = (0, 0, 0, 1, 0, 0, 0, 0, 0, 0)$のように変換してあげる必要があります.こうすることで、前回と同じコスト関数を用いることができます.それをやっているのが
y = np.array(y == label, dtype=float).reshape(1, self.m)[0]
です.
② 今回はパラメータが多いため、オーバーフィッティングが起きやすいです.それを防ぐためにコスト関数におまけを足しています:
$$
J(\theta) = \frac{1}{m}\sum_j \left[-y_j^{(i)}\log(h_\theta (x_j^{(i)})) - (1-y^{(i)})\log(1-h_\theta (x_j^{(i)}))\right] + \frac{\lambda}{m}\sum_k \theta_k^2
$$
入力$X$に依らない$\frac{\lambda}{m}\sum \theta^2$が居るため、$\theta$が大きくなりづらくなる効果があります.
③ 今回は入力のサイズも$\theta$の次元も前回と比較して桁違いに多いです.今回も$J(\theta)$の最適化問題にはfmin_cgを用いていますが、おまけで$\partial J / \partial \theta$を与えてあげることによってfmin_cgを高速化しています.そういうオプションもあるんです.
では実際にトレーニングを実行します:
v = Data()
X, y, theta = v.input_data(filename='ex3data1.mat')
c = Calc(X, y, theta)
for i in range(v.label_num):
label = next(iter_label)
print('iter_label={0}'.format(label))
theta[i] = c.optimize_theta(theta=theta[i], label=label)
この鍛え抜いた仮説関数$h_\theta$でデータセットにない手書き数字を認識させてみましょう:
In : [c.hypothesis(theta[i], hw3) for i in range(10)]
Out:
[array([ 1.34141214e-08]), # 0
array([ 2.61931452e-06]), # 1
array([ 0.00075415]), # 2
array([ 0.39339952]), # 3
array([ 9.43029863e-05]), # 4
array([ 0.00568828]), # 5
array([ 3.01025411e-11]), # 6
array([ 6.72156110e-06]), # 7
array([ 0.00318027]), # 8
array([ 0.10425808])] # 9
hw3に上の手書き数字のデータが格納されていると思ってください.3の出力が最も大きいとはいえ、0.5を超えてはいないですね、、、ヘタしたら9と誤認識する可能性もあるかもです.これでもまあいいのですが、オーバーフィッティング防止のための重みLambdaを変えてもう一度トレーニングし直してみましょう:
In : [c.hypothesis(theta[i], hw3) for i in range(10)]
Out:
[array([ 0.00398415]), # 0
array([ 0.01846233]), # 1
array([ 0.03536397]), # 2
array([ 0.58446169]), # 3
array([ 0.01247705]), # 4
array([ 0.02461416]), # 5
array([ 0.00252241]), # 6
array([ 0.02811706]), # 7
array([ 0.02264845]), # 8
array([ 0.12251284])] # 9
これはLambda=8でトレーニングした結果です.まあまあ、こんなところでしょうか.むしろこれだけシンプルなコードでちゃんと文字認識ができていることに驚くのだ!
おわりに
アドベントカレンダーに間に合わせるためにかなり端折ったざっくり内容になってしまいましたが、機械学習の香りを仄かにでも感じていただければ幸いです.Coursera本編はもっと素晴らしい内容です.興味があれば是非受講してみましょう.
ニューラルネット編に続きます...