【kaggle】Titanicから学ぶテーブルデータコンペの進め方 ～①データ分析～

はじめに

Titanicで「上位n%に入るノウハウ」、「スコアpに到達する方法」という記事は沢山ありましたが、「分析を進める時の考え方」に関する記事はほとんどありませんでした。特に初めての場合はランキングやスコアより予測結果までどうやって辿り着けば良いかを知りたい人が多いと思います。同じような悩みを抱えている人向けに書きました。データ分析初心者向けの記事です。

全パート

5つの記事で構成しています。
① データ分析(EDA)　⇐ Now
② ベースラインモデル
③ LightGBM
④ Random Forest
⑤ アンサンブル

データ分析では、各特徴量の特性や目的変数との関係性を把握してモデルに使えそうな特徴量にあたりをつけます。ベースラインモデルでは、機械学習モデルを構築する際に達成したい目標値を設定します。次に、単体モデルを作ります。最後は複数のモデルを組み合わせて精度を上げるアンサンブル学習を実施します。以上が一般的な流れです。アンサンブルに使うモデルは性質の異なるモデルがベターなので、私のように決定木系を2つだけを組み合わせることは避けた方が良さそうです。

特徴量の単純集計

モデルや特徴量を作成する前に、データをあらゆる観点から確認してデータの理解を深めます。欠損、外れ値、分布、統計量などを確認します。今回の場合だと、小数点の年齢がある、乗船運賃に0円の人がいるなどの発見があります。一般的に考えるとあり得ない値が特徴量に入っていることは多々あるので、初期段階でデータを見ておくことは重要です。

%matplotlib inline
from sklearn.preprocessing import OrdinalEncoder
import matplotlib.pyplot as plt
import pandas_profiling
import seaborn as sns
import numpy as np
import pandas as pd
import os

# 訓練、テストデータの読み込み
train = pd.read_csv("/kaggle/input/titanic/train.csv")
test = pd.read_csv("/kaggle/input/titanic/test.csv")
train.describe()

この表から次のことがわかります。

• Survived：生存率38%,死亡率62%
• Pclass：過半数がPclass=3
• Age：最年少0.42歳、最高齢80歳、幅広く分布、小数がある（小数は推定値だとデータセットの説明に記載あり）
• SibSp、Parch：過半数が１人での乗船
• Fare：無賃乗船？中央値・平均値が乖離⇒一部の人が高額料金

つづいて欠損数を確認します。

# データ分析用にtrain,testを結合
dataset = train.append(test)
# PassengerId列の削除
dataset.drop("PassengerId",axis=1, inplace = True)
print(dataset.isnull().sum().sort_values(ascending=False))

Cabin       1014
Survived     418
Age          263
Embarked       2
Fare           1
Pclass         0
Name           0
Sex            0
SibSp          0
Parch          0
Ticket         0
IsTrain        0
dtype: int64

CabinとAgeの欠損の扱いがキーポイントになりそうです。

特徴量のクロス集計

単純集計が完了したら次は、特徴量がどの程度目的変数（生存率）に寄与しているかを確認します。予測モデルに組み込んだ方が良さそうな特徴量に当たりをつけます。

def plot_df(df, f):
    """特徴量ごとの頻度と生存率の可視化
    """
   
    # figure, subpplotの作成
    fig = plt.figure()
    ax1 = fig.add_subplot(1, 1, 1)
    ax2 = ax1.twinx()

    # 頻度、生存率
    bname = "Count"
    pname = "SurvivalRate"
    ax1.bar(df.index.astype("str"), df[bname], label=bname)
    ax2.plot(df.index.astype("str"), df[pname], color='r', label=pname)

    # グラフタイトルと凡例
    ax1.set_title(f"{pname} by {df.index.name}")
    ax1.set_ylabel(bname)
    ax2.set_ylabel(pname)

    # 凡例
    ax1.legend()
    ax2.legend(loc='upper center')
    for tick in ax1.get_xticklabels():
        tick.set_rotation(45)

    plt.show()

def cal_survival_rate(f,df=train):
    """可視化用のdataframe作成
    """
    # 集計前
    train_feature = df[["Survived", f]]
  
    # 集計後
    df_feature = train_feature.groupby(f).agg(["count","mean"])["Survived"].rename(columns={"count":"Count","mean":"SurvivalRate"})
    display(df_feature)
    
    return df_feature

Sex（性別）

feature = "Sex"
plot_df(cal_survival_rate(feature), feature)

女性の方が明らかに生存率が高いので、性別は特徴量として使えそうです。

Cabin（客室番号）

客室番号は欠損数とユニークな値が多いので、生データのまま集計しても見えてくる情報が少ないです。そこで客室番号の頭文字をDeckとして新たな特徴量を作成して集計します。

feature = "Cabin"
new_feature = "Deck"

# new_feature列の生成
dataset[new_feature] = dataset[feature].str.get(0)
dataset[new_feature] = dataset[new_feature].fillna("N")

train_feature = dataset[dataset["IsTrain"]==True][["Survived", new_feature]]
plot_df(cal_survival_rate(new_feature,df=train_feature), new_feature)

• 客室番号の頭文字によって生存率が異なる
• 特に欠損値（N)の生存率が低い

頭文字によって生存率に差があるので特徴量に入れましょうという考え方だと納得感がありません。そこで、今度は頭文字によって生まれる生存率の差は、階数や前方/後方が影響していると仮説を立てて検証するプロセスが必要です。時間の都合で階数や前方/後方で特徴量を作ることはできなかったので渋々、頭文字を特徴量としました。

IsCabinNan（客室番号が欠損かどうか）

Deckで欠損値だった人は生存率が低く、そうでない人は生存率が高い傾向にあるので2値で特徴量を新たに作成します。

# Cabin
feature = "Cabin"
new_feature = "IsCabinNan"

# new_feature列の生成
dataset[new_feature] = False
dataset.loc[dataset[feature].isnull()==True, new_feature] = True

train_feature = dataset[dataset["IsTrain"]==True][["Survived", new_feature]]
plot_df(cal_survival_rate(new_feature,df=train_feature), new_feature)

Cabinが欠損している人とそうでない人には明らかな差があることがわかりました。

Ticket（チケット番号）

チケット番号の割り当てられ方は不規則なので、Cabinと同様に集計方法に工夫が必要です。チケット番号が同じ人は何かしらの共通点があって番号が一致しているので、運命を共にする可能性が高そうと判断しました。しかし、チケット番号ごとに頻度を確認するとカテゴリ数が多すぎるので諦めました。ひとまず、チケット番号が同じになった人の人数ごとに集計します。

# 同一チケットの人数
feature = "Ticket"
new_feature = "TicketGroup"

# 同一Ticketナンバーの人が何人いるか
dataset[new_feature] = dataset[feature].map(dict(dataset[feature].value_counts()))

train_feature = dataset[dataset["IsTrain"]==True][["Survived", new_feature]]
plot_df(cal_survival_rate(new_feature,df=train_feature), new_feature)

同じチケット番号が1人、5人以上で生存率が低い傾向にありました。理由がわからないので客室番号と同様に別の切り口でデータを見る必要がありそうです。とりあえずTicketの扱いには時間がかかりそうなのでこのまま進めます。

Pclass（乗客階級）

feature = "Pclass"
plot_df(cal_survival_rate(feature), feature)

Titanicが沈没した時代を考えると性別によって乗客階級が左右されている可能性もあるのではないかと考えました。そこで、性別と乗客階級でクロス集計をしました。

# クロス集計：Sex, Pclass
sex_pcls = pd.crosstab(train['Pclass'],train['Sex'], normalize='index')
display(sex_pcls)

sex_pcls.plot.bar(stacked=True) # stacked=True：積み上げ機能
plt.show()

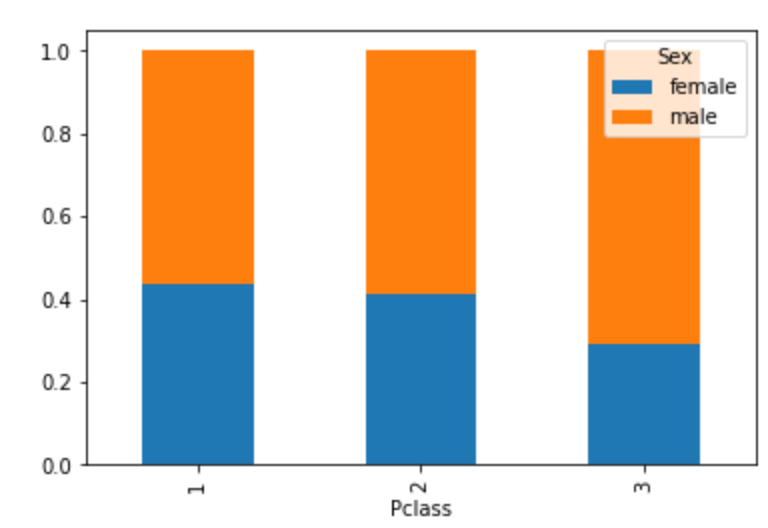
1st,2ndは同じ男女比だが2ndの方が生存率が低いので、性別というより乗客クラスが生存率に関係してそうだということが分かりました。

Embarked（出港地）

feature = "Embarked"
plot_df(cal_survival_rate(feature), feature)

出港地ごとになぜ生存率に差が出るかはピンと来なかったので、地域ごとに乗船者の階級に差がありそうという仮説をおいてクロス集計を実施しました。

# クロス集計：Embarked、Pclass
emb_pcls = pd.crosstab(train['Embarked'], train['Pclass'],normalize='index') 
emb_pcls.plot.bar(stacked=True) 
plt.show()

• Cから乗船した51%がPclass=1st⇒生存率は高そう
• Qから乗船した94%がPclass=3rd⇒生存率低そう
• Sからの乗船はPclass=3rdが55%にとどまるが、生存率はQ>Sである⇒？
  乗客クラス以外の要因が考えられそうですが深追いは辞めます。ひとまず、出港地が予測精度に寄与しそうなのでこの特徴量は使うことにします。

SibSp（同乗する兄弟と配偶者の数）

feature = "SibSp"
plot_df(cal_survival_rate(feature)

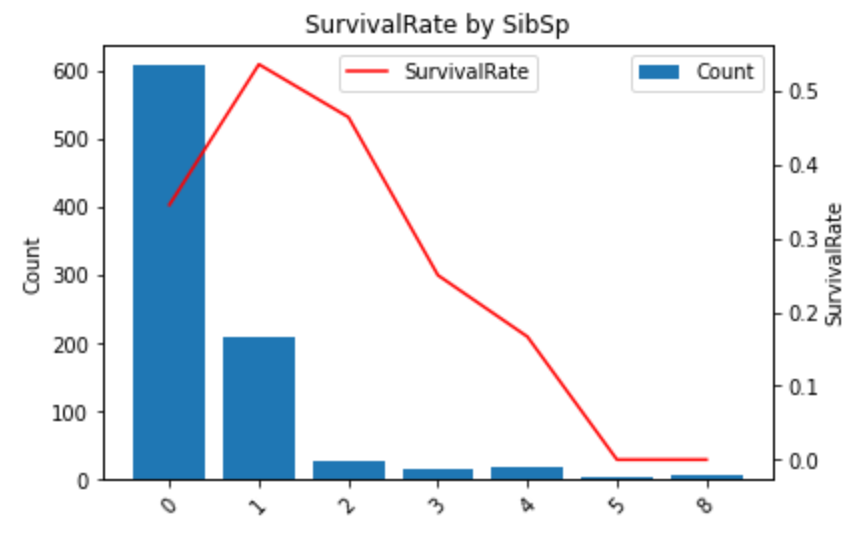
0と3以上は生存率が低くなりました。

Parch（同乗する親と子供の数）

feature = "Parch"
plot_df(cal_survival_rate(feature), feature)

0と4以上は生存率が低くなりました。
Parch、SibSpについて次の２つがわかったのでFamilyを作ると予測性能に寄与しそうだと考えました。

• 人数が増えると生存率が低下する
• どちらも家族の人数についての特徴量

Family（家族）

new_feature = "Family"
dataset[new_feature] = dataset["Parch"] + dataset["SibSp"] + 1
plot_df(cal_survival_rate(new_feature,df=train_feature), new_feature)

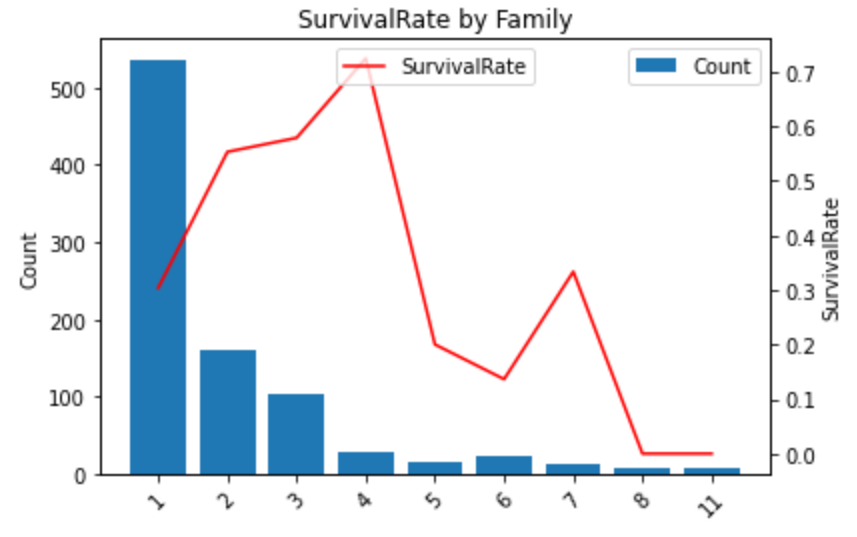
1 or 5以上で生存率が0.5以下になっており低いのでFamilyは特徴量として使えそうです。
Family=1の時、生存率が低いので新たにIsAloneという特徴量を生成します。

IsAlone（一人で乗船したかどうか）

new_feature = "IsAlone"

# 新しい列の生成
dataset[new_feature] = False
dataset.loc[dataset["Family"] == 1, new_feature] = True

train_feature = dataset[dataset["IsTrain"]==True][["Survived", new_feature]]
plot_df(cal_survival_rate(new_feature,df=train_feature), new_feature)

AgeBand（年齢幅）

Ageは連続値として与えられていますがビニング処理によってAgeBandを作りました。モデルに組み込む時は、連続値と離散値の両方を試してみて後者で予測した方が精度が向上したのでそちらを採用します。また、離散値の方が大まかな傾向を掴みやすいと思ったので連続値のグラフは省略します。

def make_age_band(df, feature):
    # AgeBandの設定
    nf = "AgeBand"
    step = 10
    lower_limit = list(range(0, 90, step))
    upper_limit = list(range(10, 100, step))

    # 新しい列の生成
    df[nf] = "00_Nan"
    for i, (lower, upper) in enumerate(zip(lower_limit, upper_limit)):
        df.loc[(lower <= df[feature]) & (df[feature] < upper), nf] = f"{str(i+1).zfill(2)}_{str(lower).zfill(2)}-{str(upper).zfill(2)}"
    
    return df, nf

dataset, new_feature = make_age_band(dataset, "Age")

train_feature = dataset[dataset["IsTrain"]==True][["Survived", new_feature]]
plot_df(cal_survival_rate(new_feature,df=train_feature), new_feature)

年齢階級ごとに生存率が大きく異なります。

• 欠損：0.29
• 0-10歳：0.61
• 70-80歳：0.0
• 80-9歳：1.0

IsAgeNanEst（欠損、推定値かどうか）

欠損/推定値の人は生存率が明らかに低いので新しい特徴量を作成します。

# 推測(年齢が〇〇.5)及び欠損値の人の生存率
feature = "Age"
new_feature = "IsAgeNanEst"

dataset[new_feature] = False
# 欠損している人
dataset.loc[dataset["Age"].isnull()==True, new_feature] = True
# 推定されている人
dataset.loc[dataset["Age"].isnull()==False, new_feature] = dataset[dataset["Age"].isnull()==False][feature].map(lambda x: True if x - int(x) > 0 else False)

train_feature = dataset[dataset["IsTrain"]==True][["Survived", new_feature]]
plot_df(cal_survival_rate(new_feature,df=train_feature), new_feature)

FareBand（乗船運賃幅）

AgeBandと同様の考え方でビニングしました。

def make_fare_band(df, feature):
    nf = "FareBand"
    # FareBandの設定:頻度に偏りがあるので階級幅を調整
    lower_limit = [0,5,10,20,30,50,70,100,200,300]
    upper_limit = [5,10,20,30,50,70,100,200,300,600] 
    
    for i, (lower, upper) in enumerate(zip(lower_limit, upper_limit)):
        df.loc[(lower <= df[feature]) & (df[feature] < upper), nf] = f"{str(i).zfill(2)}_{str(lower).zfill(3)}-{str(upper).zfill(3)}"

    return df, nf

dataset, new_feature = make_fare_band(dataset, "Fare")

train_feature = dataset[dataset["IsTrain"]==True][["Survived", new_feature]]
plot_df(cal_survival_rate(new_feature,df=train_feature), new_feature)

料金が上がるごとに生存率が上昇しています。