B-treeがMySQLで使用されている背景から、B-treeインデックスの構造、そしてそれに基づいたインデックスの使用方法の入門編です。以下の流れに沿ってまとめていきます。
- インデックスってなに?
- B-treeってなんでインデックスに使われているの?
- B-treeインデックスの構造
- インデックスの使用方法
※ 勉強をかねてまとめていることもあり、間違っている箇所がございましたら教えていただけると嬉しいです。
インデックスってなに?
全体の内容の中から特定部分を探すために使用する、本の索引のような概念のことです。これを用いることで、検索を高速化することができます。
- 特定の項目が本のどこに載っているかを確認するために索引を調べることで、全ページを順に調べなくても、その項目が登場するページ番号がわかる
- MySQLのストレージエンジンでも、インデックスが同様の方法で利用されており、インデックスのデータ構造で値を検索する
インデックスにはいくつもの種類があるのですが、MySQLで一般的に使用されているのがB-treeです。
B-treeってなんでインデックスに使われているの?
ではなぜ、インデックスにおいてB-treeがよく用いられているのでしょうか?
その説明をする前に、二分探索木とAVL木について説明します。
二分探索木
「1, 2, 3, 4, 5, 6, 7」と並んでいる数値から5がどこにあるかを検索する時、どのようにすると速く見つけることができるでしょうか?
一番単純なのは、先頭から順に探していく方法です。
ただしこれだと時間がかかるため、二分探索を用いて検索します。二分探索とは、検索したい値が中央値より小さい場合は左に進み、大きい場合は右に進みながら検索していくアルゴリズムです。
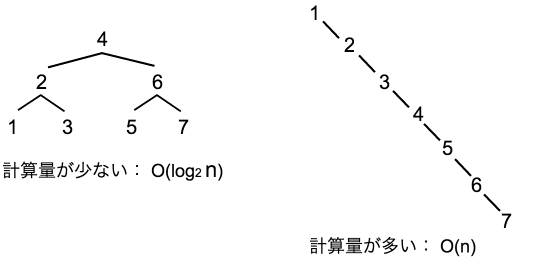
下図の左側を見て、具体的に説明していきます。
- 5は4より大きいので、右側に進みます
- 5は6より小さいので、左側に進みます
- 5が見つかりました
上図のように、二分探索しやすいように値を大小で振り分けたデータ構造が二分探索木です。
二分探索だと計算回数が少なくなりますね。
なお、検索するのにどれだけ計算する必要があるのかを表したものを計算量と言います。計算量は、N回の検索が必要な場合、O(N)と表記します。
※ 計算量には時間計算量や空間計算量などがありますが、今回は探索回数で表記しています。
- 二分探索木の高さが左右で等しい場合 (上図左側)
- 計算量 = O(log n)。計算量が少なく、最大検索数は3回。nはノード数 (入力される数列の長さ)
- 木の高さが等しくない場合 (上図右側)
- 計算量 = O(n)。計算量が多く、最大で7回の検索が必要。計算量は線形の場合に最大になる
二分探索木は検索に適したデータ構造なのですが、木の高さが揃っていない場合、検索回数が増えてしまう可能性があります。その問題に対応したのがAVL木です。
AVL木
二分探索木の場合、データの挿入や削除により、木の高さが変わります。
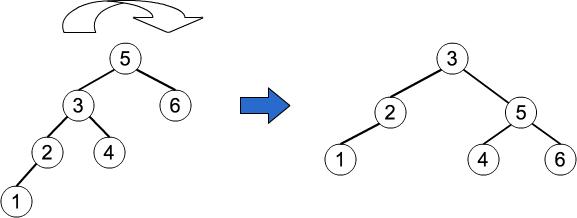
AVL木とは、木の高さに変更があった際に、二分探索木に回転という操作を行うことで、木の高さを一定にするデータ構造 (平衡木) のことです。
回転操作というのは、1つのノードを上にし、別のノードを下にし、左部分木の高さと右部分木の高さの差を調整することです。回転操作により、計算量がO(log n)になります。
このAVL木を一般化し、多分岐の平衡木構造を持ったのがB-treeになります。
なぜB-treeが使われているのか
B-treeとは、1つのノードがm個 (m>=2) の子ノードを持つことができる平衡木構造のことです。
なぜAVL木だと問題があるかというと、大規模なデータを補助記憶装置(ハードディスクなど)へ格納し検索する場合、コンピュータの処理に時間がかかってしまうためです。
ハードディスクは主記憶装置に比べ、アクセス時間が非常に長く、そのためハードディスクを効率的に扱うには、なるべくブロックの読み取り回数を少なくする必要があります。
ブロックの読み取り回数は木の深さになります。
AVL木の場合、log n 回なのに対して、B-treeの場合、log n / log m 回 (※計算は省略) になります。そのためmが大きくなるほど、処理時間に差が出てきます。
このことから、MySQLではインデックスのデータ構造にB-treeが採用されているようです。
B-treeインデックスの構造
ここまで、B-treeが使用されている理由を説明してきました。ここからはB-treeインデックスの構造について具体的に見ていきます (厳密にはB+ tree)。
インデックスの構造
B-tree構造に基づくインデックスは、ルートノードと子ノード (ブランチノード)、そしてリーフノードで構成されています。
- ルートノードと子ノードの各ページは、キー値と子ノードへのポインタを持つ
- リーフノードの各ページは、キー値とデータへのポインタを持つ (B+ treeの場合、データを持つのはリーフノードだけ)
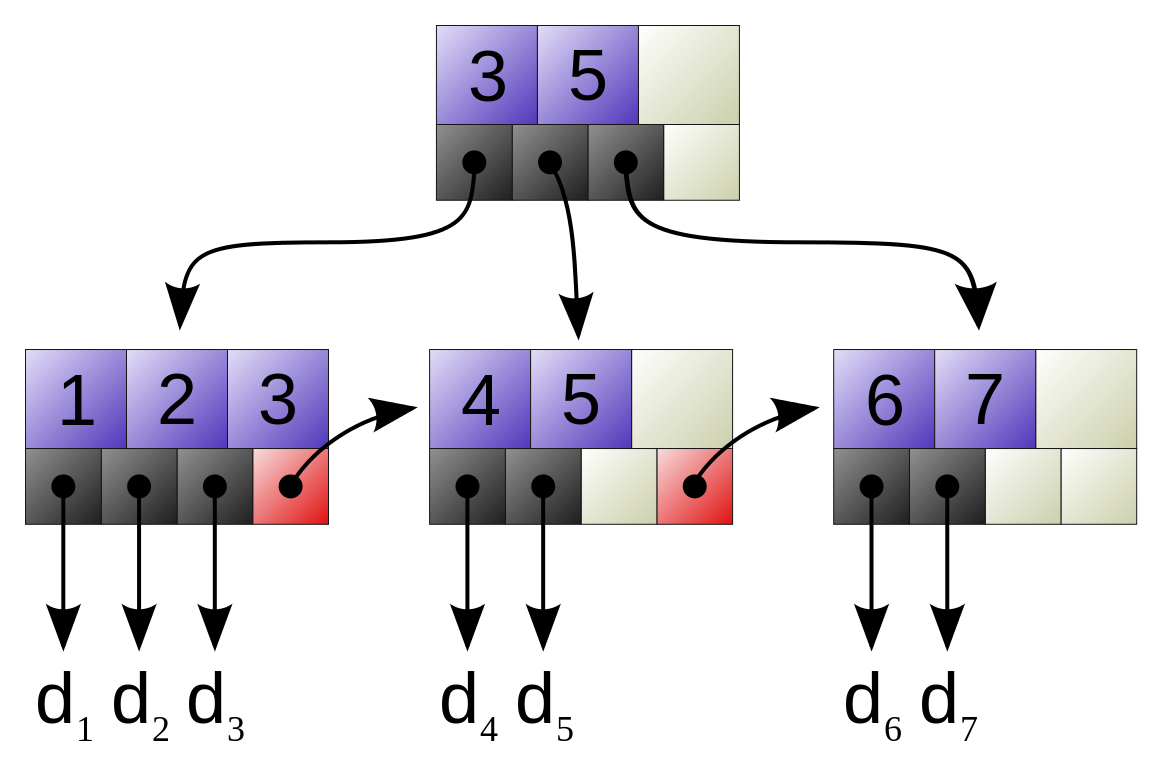
(出展:http://ja.wikipedia.org/wiki/B%2B%E6%9C%A8)
検索
検索する際、ルートノードから出発し、子ノードへのポインタに沿ってリーフノードを探します。
- まずルートノードへ行き、検索値よりも大きな値のポインタが見つかったら、その左側の子ノードへ移動する。検索値よりも大きな値が見つからない時は、キーの最大値の右側の子ノードへ移動する
- 子ノードでも同様のことを繰り返し、最終的に、目的の値が存在しないと判断するか、リーフページにたどり着く
インデックスの生成
テーブルに既にデータが入っている状態でインデックスが生成される時、内部でどのようなツリー構造が生成されるのかを見ていきます。
- はじめに、テーブルにアクセスし、CREATE TABLE文のインデックスに指定された列の順序に従って、値をソートする
- ソートされた結果をリーフノードに記録していく
- もしリーフノードがPCTFREE (Percent free: 空き領域率) に到達し、新しいリーフノードを要求したら、子ノードを生成する。その際、新しく割り当てられたリーフノードの開始値とそのノードのアドレス情報で構成された行を、子ノードに挿入する。この子ノードは最上位レベルであるため、ルートノードとなる
- 子ノードに行が積み上げられ、子ノードがPCTFREEに到達したら、新しい子ノードを割り当てる
- 新しく生成された子ノードの情報を保存するために、上位レベルの子ノードが生成される。この子ノードは最上位レベルであるためルートノードとなる。2〜5が繰り返される
インデックスの分割
インデックス行はソートされている必要があるため、既に生成されたインデックスに新しい行が挿入されると、既存のインデックスの位置を変更しなければなりません。ここでは、データの追加時にインデックスノード (B-tree内の各ページのこと) がどのように変化するのかを見ていきます。
- インデックスノードにまだ新たなキーを挿入する余裕がある場合
- キーをそのスペースに挿入する
- 既存の構造は変わらない
- PCTFREEに到達したあるインデックスノードの最後尾に値が挿入された場合
- 新しいインデックスが生成され、そこに記録される
- 既存の構造は変わらない
- PCTFREEに到達したあるインデックスノードの中間に値が挿入された場合
- ソート順を維持するために既存ブロックにその行を挿入する必要がある
- これによりPCTFREEに到達し、インデックスの分割が起こる。分割が必要なノードからキーをひとつ選択し、このキーより小さいキーだけを含むノードと、より大きいキーだけを含むノードに分割する
- この時、修正が発生する各ブロックに空き領域ができるようにしながら分割を行う
データ削除および更新
データを削除するとテーブルの行は物理的に削除されるものの、インデックスの行に対しては削除されたことを示す表示が追加されるだけです。
- リーフの範囲内の全てのデータが削除された場合
- 子ノードに存在する、該当リーフノードを示す行に削除表示が挿入される
- データを更新した場合
- 更新する元のデータがリーフより削除され、その後に挿入が実行される
- 更新後のデータを格納する先にリーフ行の空きがない場合は、リーフ分割して格納される
これらの内部処理のため、削除と更新が繰り返されると、インデックス行数は変わらず、削除インデックス行が増加していくことになります。このため、修正が頻繁に発生しない列をインデックスで通常使用します。
削除インデックス行が大量に存在すると、範囲検索を行った際に空リーフを参照するI/Oが発生するため、パフォーマンスが低下します。このような現象が発生した場合は、インデックスの再構築が必要です。
特徴
- ストレージエンジンがデータを検出するためにテーブル全体をスキャンする必要がないため、データアクセスを高速化する
- 完全なキー値、キーの範囲、キーのプレフィックスによるルックアップ (値の検索) に適している
- インデックスノードがソート済みのため、ルックアップ、ORDER BY 句、GROUP BY 句に使用できる
制限
- ルックアップがインデックス付きの列の左から始まらない場合には効果を発揮しない
- 複数列インデックスの場合、最初の範囲条件の右側に位置する列を使ってアクセスを最適化できない
インデックスの使用方法
最後に、クエリのパフォーマンスを向上させるためのインデックスの使用方法について見ていきます。
列の分離
クエリにおいてインデックス付けされた列が分離されていないと、インデックスが利用できなくなります。
列の分離とは、次の2つの状態を指します。
- 列が式の一部であってはならない
- 列が関数に含まれていてはならない
例えば次のようなクエリの場合、列が分離されておらず、インデックスを利用することができません。
mysql> SELECT id FROM table1 WHERE id + 1 = 3;
プレフィックスインデックス
非常に長い文字列にインデックスを付ける必要がある場合、値全体ではなく最初の数文字にインデックスを付けることで、記憶域を節約し、パフォーマンスを改善することができます。
- プレフィックスインデックスでは、選択性も低下するため、十分な選択性が得られる長さを持ち、記憶域を節約するくらい短いプレフィックスを選択すること
- 欠点として、ORDER BY 句や GROUP BY 句を使用するクエリにプレフィックスインデックスを使用できない
- 適切なサイズは、下記クエリで選択性を計測し、収束する値を見ることで発見できる。選択性とは、インデックス付けされた値の数と、テーブル内の行の合計数の比率のこと
mysql> SELECT COUNT(DISTINCT LEFT(c1, 3))/COUNT(*) AS sel3,
-> COUNT(DISTINCT LEFT(c1, 4))/COUNT(*) AS sel4,
-> COUNT(DISTINCT LEFT(c1, 5))/COUNT(*) AS sel5,
-> COUNT(DISTINCT LEFT(c1, 6))/COUNT(*) AS sel6
-> FROM table1;
複数列のインデックスの順序
複数列のインデックスでは、列の順序が極めて重要です。列の正しい順序は、そのインデックスを使用するクエリによって決まります。
- 等しい (=)、より大きい (>)、より小さい (<)、BETWEENなどの検索条件のWHERE句で使用されるか、結合に含まれる列を、先頭に配置する
- クエリによるカラム順序の制限がない場合、最も選択的な列をインデックスの先頭に配置する。カラム毎の選択性は下記クエリで計測する
mysql> SELECT COUNT(DISTINCT c1)/COUNT(*) AS c1_selectivity,
-> COUNT(DISTINCT c2)/COUNT(*) AS c2_selectivity
-> FROM table1;