この記事は Akatsuki Advent Calendar 2019 22日目の記事です。
はじめに
「シェーダーに興味あるけどやり方わからん!」という方を最近よく見る気がします.
私個人,もはやシェーダーしかできないくらいシェーダーが大好きなので,興味持ってくれる方が増えてとても嬉しいです!
ただ,シェーダーに関するドキュメントは他のプログラムやアーキテクチャに比べて少ないので,初めての方は取っかかりにくいと思います.
加えて,線形代数や光学の知識,グラフィックスに対するデザイン能力も必要になります.
この記事では,Unityのシェーダー(Shader Lab)が描けるようになる最低限の知識とやり方を紹介していきます.
「シェーダーに興味あるけどやり方わからん!」という方に対して少しでも力になれればと思います.
前提知識
シェーダーを描けるようになるための前提知識として,
・透視投影変換
・座標空間
・ポリゴン
・ベクトル
上記をそれぞれ紹介していきます.
あくまで「シェーダーが描けるようになる」ためなので,かなり簡潔に説明していきます.
透視投影変換
私たちは,普段目にしている3D空間を透視投影変換して1枚の画像として知覚しています.
実際に私たちが住んでいる空間にある全ての物,コンピュータで表示した仮想的な3DCG,これら全ては透視投影変換されます.
私たちが住んでいる空間(実空間)の透視投影変換
実空間で透視投影変換している例として眼球/カメラなどが挙げられます.
カメラは非常にわかりやすいですが,実空間を撮ると1枚の画像(写真)に変換していますね.
眼球もほとんど同じことをしていて,私たちは1枚の画像を何度も知覚しながら生活しています.
コンピュータ上の透視投影変換
ゲームや3D映画もカメラと同じような透視投影変換をしてディスプレイに描画しています.
ディスプレイに描画されたものは1枚の画像です.実空間のカメラと同じですね.
このように透視投影変換は3D空間を1枚の画像に変換することだと思っていてください.
座標空間
3DCGにおける空間(座標系)はいくつかありますが,
・ワールド空間
・オブジェクト空間
・クリップ空間
・スクリーン空間
上記4つを覚えていてください.
ワールド空間
3DCGにおける一番親の空間です.
このワールド空間にオブジェクトが配置されます.
オブジェクト空間
ワールド空間に配置されたそれぞれのオブジェクトが持つ固有の空間です.
大体はオブジェクトの中心がオブジェクト空間の中点になります.
(人型のモデルは足の裏が中心だったりします)
クリップ空間
ワールド空間にあるオブジェクトの内,透視投影変換する空間(カメラに納まる空間)です.
クリップ空間以外にあるオブジェクトは透視投影変換する意味がないので,
あらかじめクリップ空間にほしいオブジェクトを入れて置き,それ以外は削り取り(クリッピング)します.
スクリーン空間
座標空間の中で唯一2次元の座標系です.
透視投影変換後の1枚の画像(ディスプレイ上)の空間です.
ポストエフェクト等に扱う空間です.
ポリゴン
3DCGにおけるオブジェクトはポリゴンの集合です.
ポリゴンは3つの頂点と1つの面で構成されています.
オブジェクトはこの三角形のポリゴンを組み合わせて形状を表現しています.
 参考:https://thenounproject.com/term/3d-model-of-abstract-sphere-polygons/2303791/
https://en.wikipedia.org/wiki/Polygon_mesh
参考:https://thenounproject.com/term/3d-model-of-abstract-sphere-polygons/2303791/
https://en.wikipedia.org/wiki/Polygon_mesh
ベクトル
ベクトルは向きと大きさ(スカラー量)を表す単位として扱われることが多いです.
3DCGではさらにスカラー量を1とする正規化(Normalize)された向きだけを意味するベクトルをよく扱います.
シェーダーにおけるベクトルは
・ポリゴンの各頂点にある法線の向き
・ライトの向き
・カメラの向き
上記でよく計算されます.
シェーダーって何?
シェーダーはポリゴンに対して
・色を付ける
・テクスチャを貼る
・変形させる
・光らせる
といった効果を付加させるのがシェーダーです.
この操作をシェーディングと呼びます.
シェーダーにもいくつか種類があり,
プログラマーが操作できるステージ事に分類されています.
バーテックスシェーダー(頂点シェーダー)
バーテックスシェーダーは,入力されたポリゴンの各頂点を座標変換するシェーダーです.
もちろん透視投影変換させることがメインの目的ですが,それ以外にも
テクスチャのUV座標を参照/変換したり,頂点に内包された法線ベクトルを参照/変換することもできます.
バーテックスシェーダーで処理されたポリゴンの各頂点は,そのままフラグメントシェーダーに渡されます.
ジオメトリシェーダー(プリミティブシェーダー)
ジオメトリシェーダーは,オブジェクトの全頂点を操作するシェーダーです.
頂点の数を増減させたり,ポリゴン自体を別のポリゴンに入れ替えたり,ポリゴンの形状を変化させたりすることができます.
ジオメトリシェーダーはバーテックスシェーダーの後に計算されますが,
特殊な用途がなければジオメトリシェーダーに情報を渡さずにフラグメントシェーダーへ引き継ぐのが一般的です.
(本記事ではジオメトリシェーダーは使いません)
フラグメントシェーダー(ピクセルシェーダー)
フラグメントシェーダーは,ディスプレイの各ピクセル事に操作するシェーダーです.
(FullHD[1920x1080]のディスプレイでは2073600回フラグメントシェーダーが走ることになります)
フラグメントシェーダーはポリゴンの面に対して色を付けることがメインの目的ですが,それ以外にも
全てのレンダリングが終わった後の画像に対して,アンチエイリアス(ジャギーの軽減)やカラーグレーディング(色彩補正)を行うこともできます.
バーテックスシェーダーから渡された頂点情報を用いてディスプレイの各ピクセルに色を付けていくことで,
立体的な3D表現や,物理ベースのリアルなレンダリングが行えるわけです.
Shader "Color"
{
SubShader
{
Tags { "RenderType"="Opaque" }
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
struct VertexInput
{
float4 vertex : POSITION;
};
struct VertexOutput
{
float4 vertex : SV_POSITION;
};
VertexOutput vert(VertexInput v)
{
VertexOutput o = (VertexOutput)0;
o.vertex = UnityObjectToClipPos(v.vertex);
return o;
}
fixed4 frag(VertexOutput i) : SV_Target
{
return fixed4(1, 1, 1, 1);
}
ENDCG
}
}
}
上記のシェーダーは,白の単色を出力するシェーダーです.
それぞれの動作について順に説明していきます.
SubShader,Tags
SubShaderはTagsによってどのようにレンダリングをするのかを示します.
シェーダーがどのようにレンダリングするのかをTagsで指定することができます.
今回はUnityが標準で搭載しているRenderTypeからOpaqueを指定しています.
Opaqueは不透明の描画に適しています.
Pass
Passはシェーダーが実際に実行するパスを意味しています.
Pass内に定義されたシェーダーを計算して描画されます.
(Passを同一のシェーダー内に複数用意して,同じポリゴンに対してマルチシェーディングすることもできます)
CGPROGRAM,ENDCG
この定義で括られた範囲はUnityのシェーディング言語(ShaderLab)で定義されることを意味しています.
HLSLやGLSLといったほかのシェーディング言語で記述することもできます.
(Unityはマルチプラットフォームに対応しているため,いくつもの描画エンジンに対して互換性を持つコンパイラが内包されています)
#pragma vertex vert,#pragma fragment frag
上記のような宣言を用いて,バーテックスシェーダー/フラグメントシェーダーを指定します.
#pragma vertex vert // vert関数をバーテックスシェーダーとしてコンパイル
#pragma fragment frag // frag関数をフラグメントシェーダーとしてコンパイル
#include "UnityCG.cginc"
Unityが標準で用意しているヘルパー関数をインポートします.
これによって透視投影変換や空間から別空間の座標系への変換が簡単にできるようになります.
struct VertexInput,struct VertexOutput
バーテックスシェーダーがポリゴンから引き受ける情報(VertexInput)と,
バーテックスシェーダーがフラグメントシェーダーに渡す情報(VertexOutput)を定義しています.
今回は特殊な座標変換やライティングを行わないので,頂点情報だけ受け取っています.
後ろにくっついているセマンティクスは,その変数が何の役割を持っているのかを示しています.
POSITIONはポリゴンのオブジェクト座標を,SV_POSITIONはクリップ座標(後述)を意味しています.
(SV_POSITIONは必ず宣言しないとエラーになります)
VertexOutput vert(VertexInput v) {...}
バーテックスシェーダー関数の定義です.
(バーテックスシェーダーの実体です)
VertexInputを受け取り,VertexOutputをフラグメントシェーダーに渡している部分になります.
バーテックスシェーダー内でVertexOutputを定義し,フラグメントシェーダーに返し値として受け渡します.
o.vertex = UnityObjectToClipPos(v.vertex);
上記はポリゴンから受け取った頂点を透視投影変換後のクリップ空間に変換して,フラグメントシェーダーに引き渡す用の頂点に代入しています.
UnityCG.cginc内にあるUnityObjectToClipPos()関数を使って簡単に透視投影変換していることになります.
fixed4 frag(VertexOutput o) : SV_Target {...}
フラグメントシェーダー関数の定義です.
(フラグメントシェーダーの実体です)
VertexOutputを受け取り,最終的なピクセルの色を返します.
セマンティクスにあるSV_Targetはピクセルの色を意味しています.
(複数のレンダリングターゲットを設定したり,深度値を設定したりできます)
fixed4はfloat4の低精度版です.
色はRGBAチャンネルそれぞれで256階調の精度しか必要ないため,Unityが内部的にfloatよりも軽量で色に扱いやすいfixedを定義してくれています.
return fixed4(1, 1, 1, 1);は,色(R=1, G=1, B=1, A=1)をピクセルに渡すことを意味しています.
これによって,バーテックスシェーダーで透視投影変換されたディスプレイのポリゴン部分に白色がべた塗りされることになります.
本記事でのシェーダーについて
本記事ではシェーディングでよく扱われる有名なシェーディング技法をいくつか紹介していきます.
それぞれのシェーディング技法が個別に動作できるようなちょっとしたUberShaderを目指します.
シェーディング技法の紹介
任意の値を送る
Unityのシェーダー(Shader Lab)はPropertiesで任意の値(Uniform変数)をセットすることができます.
シェーダー内でProperties{}を記述することで利用可能です.
変数名 ("表示名", 型) = 初期値のように宣言します.
Shader LabのUniform変数はアンダースコア+大文字開始で記述することが一般的です.
Shader "Color"
{
Properties
{
[Header(Main)]
_MainColor ("Main Color", Color) = (0, 0, 0, 1)
}
...
}
上記のようにSubShaderの上に記述すると,UnityのInspector上でMainColorが表示されます.
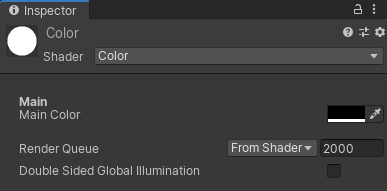
このままでは色を編集しても反映されないので,指定した色になるようにシェーダーに追記します.
Shader "Color"
{
...
SubShader
{
...
Pass
{
...
#include "UnityCG.cginc"
fixed4 _MainColor;
...
fixed4 frag(VertexInput i) : SV_Target
{
return _MainColor;
}
...
}
これで指定された色が反映されるようになります.
| インスペクタ | レンダリング結果 |
|---|---|
 |
 |
fixed4 _MainColor;はUniform変数と呼ばれ,外部から引き取るパラメータを意味しています.
return _MainColor;で受け取った値をそのままピクセルへ出力させています.
テクスチャを貼る
次にテクスチャマッピングを行います.
[任意の値を送る](### 任意の値を送る)と同様にUniform変数としてテクスチャをProperties内に定義し,
uniform変数の受け取りを宣言します.
// Propertiesにテクスチャを宣言
Properties
{
_MainColor ...
_MainTexture ("Main Texture", 2D) = "white" {} // 何も入っていない場合は白色のテクスチャとして扱われる
}
// Uniform変数の受け取り
fixed4 _MainColor;
sampler2D _MainTexture;
float4 _MainTexture_ST; // _MainTextureのタイリングとオフセット値が格納されている
バーテックス構造体の中身にuvを追加します.
struct VertexInput
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct VertexOutput
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
バーテックスシェーダー内で,フラグメントシェーダーにポリゴンのuv座標をそのまま渡します.
VertexOutput vert(VertexInput v)
{
VertexOutput o = (VertexOutput)0;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = v.uv;
return o;
}
フラグメントシェーダー内でテクスチャマッピングを行います.
fixed4 frag(VertexOutput i) : SV_Target
{
// _MainTextureを貼るためのuvを定義します.
// _MainTextureに設定されたタイリングとオフセットを反映させる式は下のようになります
// uv = uv * タイリング + オフセット
float2 mainUv = i.uv * _MainTexture_ST.xy + _MainTexture_ST.zw;
// _MainTextureをマッピングします.
// tex2D()を使うことで,テクスチャとuvから任意にマッピングさせることができます.
// 最後に_MainColorを乗算することでTint Colorとして動作させます.
return tex2D(_MainTexture, mainUv) * _MainColor;
}
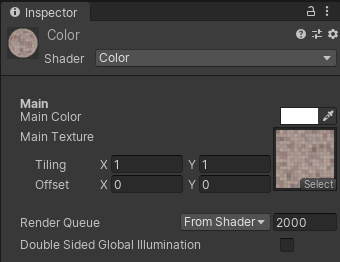
レンダリング結果は以下のようになります
| テクスチャ | インスペクタ | レンダリング結果 |
|---|---|---|
 |
 |
 |
Diffuse(拡散反射)
次はDiffuseシェーディングについて紹介します.
Diffuseは拡散させる,放散するという意味です.
私たちが普段目にしている物体のほとんどはこのDiffuseの影響を受けて立体的に見えています.
とある光源から放たれた光は,物体の表面で反射して私たちの目に入るため,私たちは物体を知覚することができます.
この時の物体の明るさは,光と表面の法線方向(Normal)が完全に反対向きの時に1番明るくなり,
逆に完全に一致すると1番暗くなります.
(光源方向に近い面は明るく,反対側は暗くなるということです)
この計算式をシェーダーにいれることで,べた塗りではなく立体的な(形状がはっきりとした)結果を得ることができます.
ここからは少し複雑なので,わかりやすく説明していきます.
このシェーダーで追加で必要な要素は
・法線
・ライトの向き
・内積
・Diffuseの計算式
の4つになります.
法線
ポリゴンの法線は各頂点に1つずつ内包されています.
法線はその頂点がどの向きに存在しているのか,のパラメータになります.

ライトの向き
通常はメインの1番強い光源(UnityではDirectional Light)の向きを指します.
内積
線形代数でよく登場する内積です.
シェーダーで扱うベクトルは基本的に正規化された単位ベクトルです.
内積は2つのベクトルに対する二項演算ですが,計算結果は
「2つの単位ベクトルの向きがどれくらい一緒なのか?」
を意味しています.
(シェーダーで使う内積への理解はこんな感じで大丈夫です)
2つの単位ベクトル $\boldsymbol{a}$,$\boldsymbol{b}$ について,
2つの単位ベクトルの向きが一致:$\boldsymbol{a}$・$\boldsymbol{b}$ $= 1$
2つの単位ベクトルの向きが直交:$\boldsymbol{a}$・$\boldsymbol{b}$ $= 0$
2つの単位ベクトルの向きが反対:$\boldsymbol{a}$・$\boldsymbol{b}$ $= -1$
2つの単位ベクトルの向きは1に近いほど一致しており,-1に近いほど反対を向いているということになります.
Diffuseの計算式
法線,ライトの向き,内積,座標系がなんとなく理解できていればDiffuseの計算式はすぐに理解できると思います.
Diffuseの色 = max(0, 法線とライトの逆向きの内積) × 元の色
結論から言うと上記のような式になります.
max(a, b)はaまたはbの内大きいほうの値を返します.上記の式の場合は法線とライトの逆向きの内積を最小値0で取得することと同義です.
法線とライトの逆向きの内積 × 元の色は,まさにDiffuse章の最初で述べた「この時の物体の明るさは,光と表面の法線方向(Normal)が完全に反対向きの時に1番明るくなり,逆に完全に一致すると1番暗くなる」と同じ意味です.
上記の式では法線とライトの向きが直交(内積が0)の時に真っ黒になります.球を描画する場合は,球全体の内の半分が真っ黒になる,ということになります.
具体的なシェーダーのコードと出力結果を見てみましょう.
struct VertexInput
{
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
// ポリゴンから法線を取得します.この時点ではオブジェクト座標のベクトルです.
// セマンティクスがNORMALだと法線を自動で取得してくれます.
float3 normal :NORMAL;
};
struct VertexOutput
{
float4 vertex : SV_POSITION;
float2 uv : TEXCOORD0;
// フラグメントシェーダーに渡す法線はワールド座標へ変換します.
// ベクトル同士の計算は座標系を合わせる必要があるため,
// シェーダーではワールド座標に変換してベクトル同士の計算を行うことが多いです.
// フラグメントシェーダーに渡す値はこちらが自由に設定するものなので,TEXCOORD(数値)を使います.
float3 normalWS : TEXCOORD1;
};
VertexOutput vert(VertexInput v)
{
VertexOutput o = (VertexOutput)0;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = v.uv;
// UnityObjectToWorldNormalを使うと,オブジェクト座標系の法線をワールド座標系に変換することができます.
o.normalWS = UnityObjectToWorldNormal(v.normal);
return o;
}
fixed4 frag(VertexOutput i) : SV_Target
{
// World Space Directions
// Lはワールド座標のライトの向き,Nはワールド座標の法線の向きです.
// normalize()は正規化を意味していて,スカラー量が1になるようにベクトルの値を調整してくれます.
// と同時に,ShaderLabでは特殊なことをやってくれますが,割愛します.
float3 L = normalize(-_WorldSpaceLightPos0.xyz);
float3 N = normalize(i.normalWS);
// Final Color of This Shader
fixed4 finalColor = fixed4(0, 0, 0, 1);
// Texture Mapping
float2 mainUv = i.uv * _MainTexture_ST.xy + _MainTexture_ST.zw;
finalColor = tex2D(_MainTexture, mainUv) * _MainColor;
// Diffuse Shade
fixed3 diffColor = max(0, dot(N, -L)) * finalColor.rgb;
finalColor.rgb = diffColor;
return finalColor;
}
| Diffuse無し | Diffuse有り |
|---|---|
 |
 |
Diffuseが入るだけで立体的に見え,よくあるシェーディングっぽくなったのではないでしょうか.
ハーフランバート
通常のDiffuseでは反対側が完全に暗くなってしまいます.
ハーフランバートという計算式で全体の明るさを良い感じに底上げすることができます.
// _DiffuseShadeはUniform変数(FloatまたはRange(0.0, 1.0)とか便利です)として登録しておいてください!
// Diffuse Shade
fixed3 diffColor = max(0, dot(N, -L) * _DiffuseShade + (1 - _DiffuseShade)) * finalColor.rgb;
finalColor.rgb = diffColor;
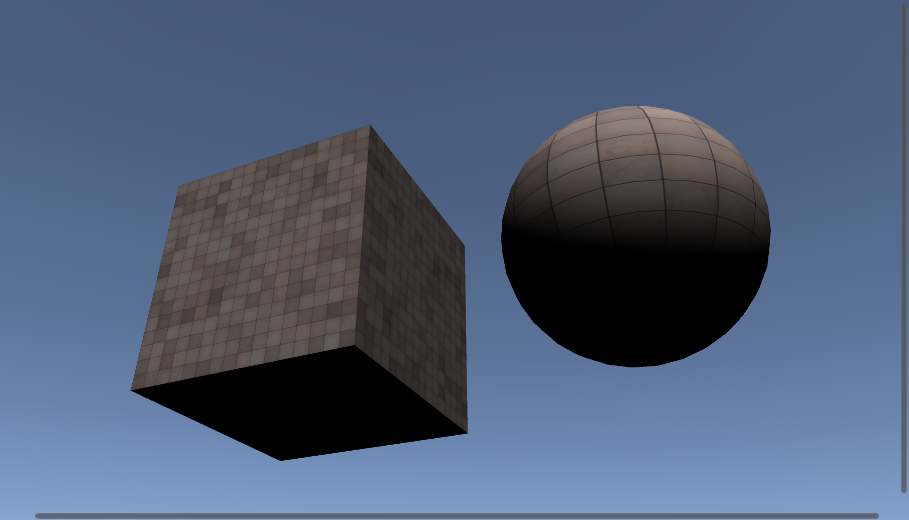
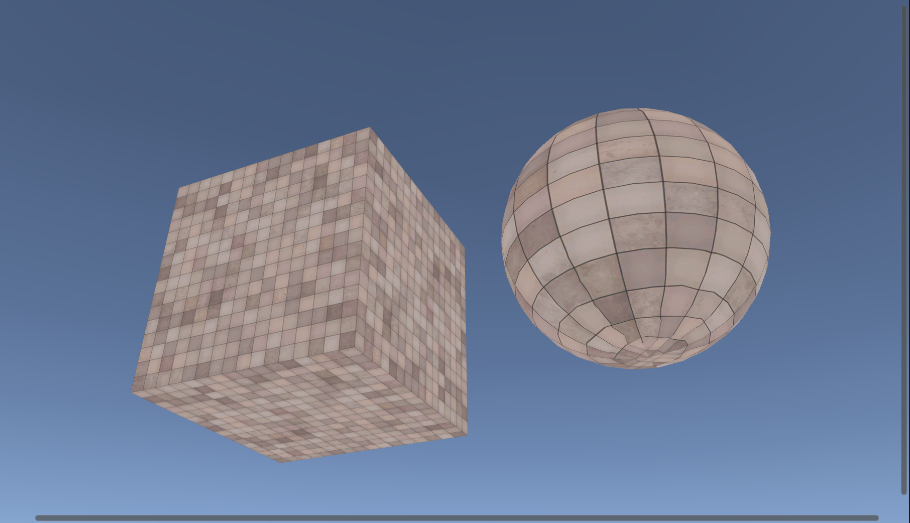
上記の計算式によって,
- _DiffuseShade = 1 のとき通常のDiffuse
- _DiffuseShade = 0.5 のときハーフランバート
- _DiffuseShade = 0 のときDiffuseライティング無し
という結果が得られます.
(内積の結果を比率で左右しているだけです)
| _DiffuseShade = 1 | _DiffuseShade = 0.5 | _DiffuseShade = 0 |
|---|---|---|
 |
 |
 |
Specular(鏡面反射)
次にSpecularについて紹介します.
Specularは鏡面反射のことを指します.
このライティングによって,光沢のある質感を表現することができるようになります.
Diffuseは立体感を,Specularは金属っぽい光沢/艶を意味します.
このシェーダーで追加で必要な要素は
・ビューベクトル
・ハーフベクトル
・Specularの計算式
の3つです.
ビューベクトル
視点がどの方向を向いているのか,のベクトルになります.
一般的にはUnity上のカメラのワールド座標系での向きを指します.
ハーフベクトル
逆ビューベクトルと逆ライトベクトルを足し合わせたベクトルです.
Specularの計算式に利用します.
Specularの計算式
Specularの色は,Diffuseによって付けられた色の上に加算します.
(Specularは物体の色ではなく,あくまで強いライトの色が反射しているだけだからです)
Specularの色 = max(0, 法線とハーフベクトルの内積) × ライトの色
結論から言うと上記のような式になります.
Specularは**「物体を鏡としてライトを見ている」**ことと同義です.
物体に光沢があればあるほど反射するため,ライトがより強調されて鋭く発光したように見えます.

図のようにハーフベクトル(逆ビューベクトル+逆ライトベクトルを正規化したベクトル)が,法線と一致していればするほどSpecular光が目に入ることになります.
この一致度合を内積を用いて求めます.
具体的なシェーダーのコードと出力結果を見てみましょう.
Properties
{
[Header(Specular)]
_SpecularColor ("Specular Color", Color) = (1, 1, 1, 1)
_SpecularPower ("Specular Power", Range(0.1, 20.0)) = 20.0
}
struct VertexOutput
{
float4 vertex : SV_POSITION;
float2 uv : TEXCOORD0;
float3 normalWS : TEXCOORD1;
// 頂点のワールド座標
float4 vertexWS : TEXCOORD2;
};
VertexOutput vert(VertexInput v)
{
...
// mul(a, b)は行列の掛け算です.
// unity_ObjectToWorldはオブジェクト座標系からワールド座標系へ変換する行列です.
o.vertexWS = mul(unity_ObjectToWorld, v.vertex);
return o;
}
fixed4 frag(VertexOutput i) : SV_Target
{
// World Space Directions
...
// カメラのワールド座標から頂点のワールド座標へのベクトルがビューベクトルになります.
float3 V = normalize(i.vertexWS - _WorldSpaceCameraPos);
// 逆ビューベクトルと逆ライトベクトルの和がハーフベクトルになります.
float3 H = normalize(-L + -V);
// Final Color of This Shader
// Texture Mapping
// Diffuse Shade
// Specular Addition
// pow(a, b)はaのb乗を意味します.
// Specular計算の全体を累乗していくことで,鋭さを得ることができます.
fixed3 specColor = pow(max(0, dot(N, H)), _SpecularPower) * _SpecularColor.rgb;
finalColor.rgb += specColor;
return finalColor;
}
| インスペクタ | レンダリング結果 |
|---|---|
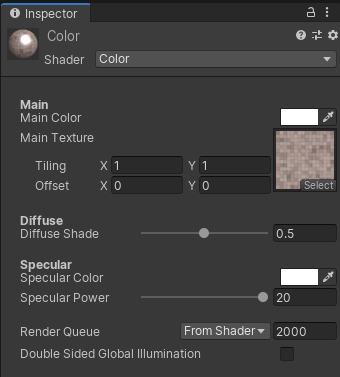 |
 |
球にライトの反射が映り込み,金属っぽい質感を得られました.
このままでは元のテクスチャと相性が悪いので,Specular光の光量と鋭さを抑えてみます.
| インスペクタ | レンダリング結果 |
|---|---|
 |
 |
それっぽくなったのではないでしょうか.
リムライティング
次にリムライティングについて紹介します.
リムライティングは,モデル後方からカメラ側に向かってライトが当たっているときに生じる効果で,
モデルの輪郭部分がライティングされたような見た目になります.
法線/ライトベクトル/ビューベクトルを用いて実装することができます.
リムライティングの計算式
初めに,ライトの向きを考慮せずに常に輪郭部分にリムライティングする計算式を紹介します.
リムライト色 = 1.0 - saturate(法線と逆ビューベクトルの内積)
saturateは引数を0~1でclampする関数です.
法線と逆ビューベクトルの内積は下図のような意味となります.

上記を1.0から引くことによって,オブジェクトの端に行けば行くほど値が1に近づくような数値になります.
リムライトの値は0~1のため,累乗して値を顕著に変化させることでSpecularの鋭さのようなパラメータを与えることもできます.
これに任意の色を乗算してオブジェクトの色に加算することで,リムライティングを得ることができます.
リムライト色 = pow(1.0 - saturate(法線と逆ビューベクトルの内積), 鋭さ) * 任意の色
具体的なシェーダーのコードと出力結果を見てみましょう.
Properties
{
[Header(Rim Lighting)]
_LimRightColor ("Lim Right Color", Color) = (1, 1, 1, 1)
_RimLightPower ("Lim Right Power", Range(0.1, 20.0)) = 5.0
}
fixed4 frag(VertexOutput i) : SV_Target
{
// World Space Directions
// Final Color of This Shader
// Texture Mapping
// Diffuse Shade
// Specular Addition
// Rim Lighting Addition
fixed3 rimColor = pow(1.0 - saturate(dot(N, -V)), _RimLightPower)* _RimLightColor;
finalColor.rgb += rimColor;
return finalColor;
}
| インスペクタ | リムライト無し | リムライト有り |
|---|---|---|
 |
 |
 |
このままでは光源に関係なく常に周囲がリムライティングされてしまうため,少し不自然です.
光源方向を考慮したリムライティングにしてみましょう.
リムライトは「逆ビューベクトルと法線の内積の逆数」で視点方向から見た輪郭部分を抽出しました.
これに加えて,ライト方向を裏から見た輪郭部分だけを抽出すれば良いわけです.

光源方向リムライティングの計算式は次のようになります.
rim = 1 - saturate(法線と逆ビューベクトルの内積)
rim *= 1 - saturate(法線とライトベクトルの内積)
リムライト色 = pow(rim, 鋭さ) * 任意の色
具体的なシェーダーのコードと出力結果を見てみましょう.
fixed4 frag(VertexOutput i) : SV_Target
{
// World Space Directions
// Final Color of This Shader
// Texture Mapping
// Diffuse Shade
// Specular Addition
// Rim Lighting Addition
float rim = 1.0 - saturate(dot(N, -V));
rim *= (1.0 - saturate(dot(N, L))); // ライトの裏側から見た輪郭部分だけ抽出
fixed3 rimColor = pow(rim, _RimLightPower) * _RimLightColor;
finalColor.rgb += rimColor;
return finalColor;
}
| 通常のリムライト | 光源方向リムライト |
|---|---|
 |
 |
実は上記のリムライトでは,ライトベクトルとビューベクトルが反対向きの時にリムライトが強く表示されなくなります.
| 光源方向から見たとき | 反光源方向から見たとき |
|---|---|
 |
 |
光源方向リムライトの計算式に対して,さらにビューベクトルとライトベクトルが反対の向きほど強くなるような式を追記します.
ビューベクトルと逆ライトベクトルが一致しているときに反対を向いていると言えるので,dot(V, -L)を条件に足すだけで良いです(計算結果はsaturateして0~1にclampします).
rim *= saturate(1.0 - saturate(dot(N, L)) + dot(V, -L));
出力結果は以下のようになります.
| 光源方向から見たとき | 反光源方向から見たとき |
|---|---|
 |
 |
光源方向をしっかり考慮できたリムライトを得ることができました.
キューブマッピング,マスク,On/Off/Blend
オブジェクトが鏡面の場合,鏡のように背景が映り込んだような見た目になります.
シェーダーでは鏡面の表現で
・GI(グローバルイルミネーション)
・スフィアマッピング
・キューブマッピング
等のテクニックが利用されています.
GIはリアルタイムでクオリティの高い結果を得られますが,設定が複雑で処理負荷が高いです.
スフィアマッピングは比較的軽いですが,一点から見た景色を映り込ませているため,カメラを動かしても反射面が変わらない(特に球の場合)という欠点があります.
本記事ではその中間のクオリティと処理負荷のキューブマッピングを紹介します.
実は,ShaderLabではキューブマッピングをかなり簡単に実装することができます.
したがってキューブマップの詳しい動作についてはここでは記述しません.
(キューブマップをわかりやすく解説した記事はこちらをご参考ください.これ以上ないほどにわかりやすい素晴らしい記事です)
このキューブマップの項では,シェーダーでよく使うマスクという概念と,
キューブマップのような部分的に使える特殊なライティングのOn/Off/Blendを紹介します.
本記事で作成しているような様々な機能を内包したシェーダーでは,オブジェクトごとにライティングを使い分ける必要があります.
その使い分けの方法として,マスクとOn/Off/Blendがあるようなイメージです.
キューブマッピング
まず初めにShaderLabでのキューブマッピングについてです.
キューブマップ用の6面のテクスチャをCUBEとしてUnityへインポートして使用します.
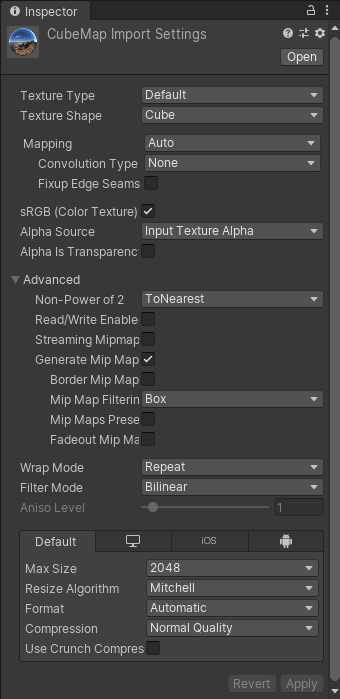
具体的なシェーダーのソースコードは以下のようになります.
Properties
{
[Header(Cube Map)]
_CubeMapTexture ("Cube Map Texture", CUBE) = "black" {}
}
SubShader
{
Pass
{
...
// Uniform変数としてインポート
// ShaderLabが用意した関数を使ってインポートします
UNITY_DECLARE_TEXCUBE(_CubeMapTexture);
...
fixed4 frag(VertexOutput i) : SV_Target
{
// World Space Direction
// Final Color of This Shader
// Texture Mapping
// Diffuse Shade
// Cube Map
// ビューベクトルと法線から,キューブマップテクスチャをサンプリングします
float3 refDir = reflect(V, N);
fixed3 cubemapColor = UNITY_SAMPLE_TEXCUBE(_CubeMapTexture, refDir);
finalColor.rgb = cubemapColor;
// Specular Addition
// Rim Lighting Addition
return finalColor;
}
}
}
出力結果は以下のようになります.
| テクスチャ | レンダリング結果 |
|---|---|
| こちらの画像を使わさせていただきました |  |
マスク
マスクはキューブマップのような特殊なライティングをとある部分にだけ適応したい場合に便利です.
通常はマスク用のテクスチャを用いることが多いですが,容量削減のために低解像度のテクスチャを使用したり,
RGBAのうちRだけを用いたテクスチャを使用したり,頂点カラー(頂点が法線とは別に固有で持っている色パラメータ)に疑似的に格納したりします.
今回は通常のテクスチャを用いてキューブマッピングにマスクをかけてみます.
原理は非常に単純で,とあるUV座標点のテクスチャの色が0に近いほど元の色,1に近いほどキューブマップの色にするといった感じです.
この処理はlerpを使って実装することができます.
しきい値(0~1) = tex2D(マスクテクスチャ, uv);
出力色 = lerp(元の色, キューブマップの色, しきい値);
式にすると上記のようになります.
Properties
{
[Header(Cube Map)]
_CubeMapTexture ("Cube Map Texture", CUBE) = "black" {}
_CubeMapMask ("Cube Map Mask", 2D) = "white" {}
}
SubShader
{
Pass
{
...
// Uniform変数としてインポート
UNITY_DECLARE_TEXCUBE(_CubeMapTexture);
sampler2D _CubeMapMask;
...
fixed4 frag(VertexOutput i) : SV_Target
{
// World Space Direction
// Final Color of This Shader
// Texture Mapping
// Diffuse Shade
// Cube Map
float3 refDir = reflect(V, N);
fixed3 cubemapColor = lerp(finalColor.rgb, UNITY_SAMPLE_TEXCUBE(_CubeMapTexture, refDir), tex2D(_CubeMapMask, i.uv));
finalColor.rgb = cubemapColor;
// Specular Addition
// Rim Lighting Addition
return finalColor;
}
}
}
| インスペクタ | レンダリング結果 |
|---|---|
 |
 |
On/Off/Blend
マスクとは別に,キューブマップのような特殊なライティングをOn/Off/Blendする場合も
lerpを用いて実装することができます.
lerpの最後の引数をRange(0.0, 1.0)のUniform変数として渡すだけです.
Properties
{
[Header(Cube Map)]
_CubeMapTexture ("Cube Map Texture", CUBE) = "black" {}
_CubeMapMask ("Cube Map Mask", 2D) = "white" {}
_CubeMapBlend ("Cube Map Blend", Range(0.0, 1.0)) = 0.0
}
SubShader
{
Pass
{
...
// Uniform変数としてインポート
UNITY_DECLARE_TEXCUBE(_CubeMapTexture);
sampler2D _CubeMapMask;
float _CubeMapBlend;
...
fixed4 frag(VertexOutput i) : SV_Target
{
// World Space Direction
// Final Color of This Shader
// Texture Mapping
// Diffuse Shade
// Cube Map
float3 refDir = reflect(V, N);
fixed3 cubemapColor = lerp(finalColor.rgb, UNITY_SAMPLE_TEXCUBE(_CubeMapTexture, refDir), tex2D(_CubeMapMask, i.uv));
finalColor.rgb = lerp(finalColor.rgb, cubemapColor, _CubeMapBlend);
// Specular Addition
// Rim Lighting Addition
return finalColor;
}
}
}
| インスペクタ | レンダリング結果 |
|---|---|
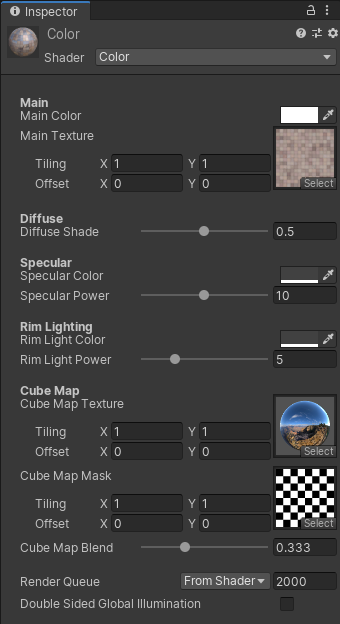 |
 |
トゥーンレンダリング,マルチコンパイル
トゥーンレンダリング
これまでのシェーディングは物理ベースとまではいかない(経験則から算出した式だから)ものの,現実世界で起こりうる表現を紹介してきました.ここからはNPR(Non-Photorealistic Rendering)のシェーディングの中で一番よく扱われるトゥーンレンダリングについて紹介します.
トゥーンレンダリングによる陰影はDiffuseと異なり,境界がはっきりとしたべた塗りの陰影になります.アニメやセル画に近い表現によく扱われ,2D映画やセルルックのゲームとの相性が良いシェーディング技法です.

参考:https://ja.wikipedia.org/wiki/%E3%83%88%E3%82%A5%E3%83%BC%E3%83%B3%E3%83%AC%E3%83%B3%E3%83%80%E3%83%AA%E3%83%B3%E3%82%B0
トゥーンレンダリングはDiffuseの計算式を利用して,しきい値から陰影を判定します.ハーフランバートではDiffuseは0~1(一番暗いところ~一番明るいところ)が格納され,その値から色を算出していました.ここにしきい値を設け,明るいところ/暗いところを2極化させます.
例えばしきい値が0.5のとき,Diffuseが0.5以下のとき影色をべた塗り,0.5より大きいとき明るい色をべた塗するといった感じです.計算式は以下のようになります.
float d = dot(N, -L) * 0.5 + 0.5;
finalColor = lerp(明るい色, 影の色, step(d, しきい値));
マルチコンパイル
同時に,シェーダーのマルチコンパイルを少しだけ紹介します.
本記事で作成しているような様々なライティングやシェーディング技法を内包したシェーダーでは,各機能ごとに使用/不使用を切り分けたい場合があります.通常Propertiesでbooleanを定義し,if文で分岐すればいいだけですが,シェーダー内部のif文分岐は処理負荷の原因となります.シェーダーは1枚の画像をレンダリングするために何回も処理が走るため,なるべく同じシェーダーを実行するべきです.if文がシェーダーのコード内に存在すると,シェーダーが走るたびに条件によって命令を変更する必要があり,数百万回以上走るシェーダーではかなりのボトルネックになってしまいます.
そこで,シェーダーのマルチコンパイルを利用します.マルチコンパイルでとある条件に対して複数のシェーダーをコンパイル(バリアントを生成)し,内部的に違うシェーダーとして扱うことで条件分岐を回避します.
ただし,マルチコンパイルの条件が多ければ多いほど組み合わせの数でバリアントが生成されてしまうため,シェーダーコンパイルが長引いたり容量圧迫の原因となってしまうため注意です.
マルチコンパイルの強みはif文回避だけでなく,別シェーダーとしてコンパイルされるため使用しない処理はコンパイルも実行もされないところにあります.場合によってマルチコンパイルする/しないを使い分けて,軽量なシェーダーを目指しましょう.
シェーダーのマルチコンパイルをしたい場合は,
#pragma shader_feature KEY_WORD
...
#ifdef KEY_WORD
(1)の処理
#else
(2)の処理
#endif
上記のように扱います.
今回はテクスチャマッピングとトゥーンレンダリングをマルチコンパイルしてみます.
具体的なシェーダーのコードを見てみましょう.
Properties
{
...
[Header(Toon Rendering)]
[Toggle(USE_TOONRENDERING)] _UseToonRendering ("Use Toon Rendering", Int) = 0 // USE_TOONRENDERINGをキーワードとしてマルチコンパイルします
_BaseTexture ("Base Texture", 2D) = "white" {}
_BaseColor ("Base Color", Color) = (1, 1, 1, 1)
_Step1stShade ("Step 1st Shade", Range(0.0, 1.0)) = 0.0
_1stShadeTexture ("1st Shade Texture", 2D) = "white" {}
_1stShadeColor ("1st Shade Color", Color) = (1, 1, 1, 1)
}
...
SubShader
{
Pass
{
CGPROGRAM
#pragma shader_feature USE_TOONRENDERING
...
fixed4 frag(VertexOutput i) : SV_Target
{
// World Space Directions
// Final Color of This Shader
#ifdef USE_TOONRENDERING
// Toon Rendering
float d = dot(N, -L) * 0.5 + 0.5;
fixed4 baseColor = tex2D(_BaseTexture, i.uv * _BaseTexture_ST.xy + _BaseTexture_ST.zw) * _BaseColor;
fixed4 firstShadeColor = tex2D(_1stShadeTexture, i.uv * _1stShadeTexture.xy + _1stShadeTexture.zw) * _1stShadeColor;
finalColor = lerp(baseColor, firstShadeColor, step(d, _Step1stShade));
#else
// Texture Mapping
#endif
...
}
}
}
上記によってシェーダーは2つのバリアントをコンパイルします.
トゥーンレンダリングではしばしば1号陰だけでなく,2号陰まで使用する場合があります.同じ計算式で2号陰まで追記してみましょう.
Properties
{
...
[Header(Toon Rendering)]
[Toggle(USE_TOONRENDERING)] _UseToonRendering ("Use Toon Rendering", Int) = 0 // USE_TOONRENDERINGをキーワードとしてマルチコンパイルします
_BaseTexture ("Base Texture", 2D) = "white" {}
_BaseColor ("Base Color", Color) = (1, 1, 1, 1)
_Step1stShade ("Step 1st Shade", Range(0.0, 1.0)) = 0.0
_1stShadeTexture ("1st Shade Texture", 2D) = "white" {}
_1stShadeColor ("1st Shade Color", Color) = (1, 1, 1, 1)
_Step2ndShade ("Step 2nd Shade", Range(0.0, 1.0)) = 0.0
_2ndShadeTexture ("2nd Shade Texture", 2D) = "white" {}
_2ndShadeColor ("2nd Shade Color", Color) = (1, 1, 1, 1)
}
...
SubShader
{
Pass
{
fixed4 frag(VertexOutput i) : SV_Target
{
// World Space Directions
// Final Color of This Shader
#ifdef USE_TOONRENDERING
// Toon Rendering
float d = dot(N, -L) * 0.5 + 0.5;
fixed4 baseColor = tex2D(_BaseTexture, i.uv * _BaseTexture_ST.xy + _BaseTexture_ST.zw) * _BaseColor;
fixed4 firstShadeColor = tex2D(_1stShadeTexture, i.uv * _1stShadeTexture.xy + _1stShadeTexture.zw) * _1stShadeColor;
fixed4 secondShadeColor = tex2D(_2ndShadeTexture, i.uv * _2ndShadeTexture.xy + _2ndShadeTexture.zw) * _2ndShadeColor;
finalColor = lerp(baseColor, firstShadeColor, step(d, _Step1stShade));
finalColor = lerp(finalColor, secondShadeColor, step(d, _Step2ndShade));
#else
// Texture Mapping
#endif
}
}
}
| インスペクタ | レンダリング結果 |
|---|---|
 
|
 |
マルチパス,アウトライン
マルチパス
ShaderLabでは,1つのシェーダーがいくつものPassを持つことができ,より複雑なシェーディングを施すことができます.Passの追加はSubShader{}内にPass{}を追記するだけです.この項ではこのマルチパスシェーディングを用いてアウトラインの描画を紹介します.
アウトライン
アニメ調やセル画を目指すには必須のシェーディングです.オブジェクトの輪郭部分にラインを描画し,線画のような表現ができるようになります.アウトラインを描画する方法はいくつかありますが,本項では背面法を用います.背面法は実装が簡単で比較的軽量なアウトラインの描画方法です.
1つ目のアウトラインを元のオブジェクトからやや大きめにアウトラインの色べた塗で描画し,2つ目に通常通りライティングを施したオブジェクトを描画してラインを表現します.**1つ目に描画したオブジェクトは前面をカリングして裏面だけが描画されるようにします.**こうしないと膨張したオブジェクトの中に通常のオブジェクトが描画されるため,アウトラインの色だけが表示されてしまいます.
カリングを行うことで反対面を描画する必要がなくなるため描画コストが下がります.ついでに,通常のシェーダーPassは逆に裏側(オブジェクトの内側)をカリングしてしまいましょう(オブジェクトの内側は半透明でない限り通常見えませんからね).
1つ目のパスではバーテックスシェーダーで頂点を法線方向に膨張させます.
Properties
{
[Header(Outline)]
_OutlineWidth ("Outline Width", Range(0.0, 1.0)) = 0.02
_OutlineColor ("Outline Color", Color) = (0, 0, 0, 1)
}
SubShader
{
// Outline Pass
Pass
{
// 前面をカリングする
Cull Front
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#include "UnityCG.cginc"
float _OutlineWidth;
fixed4 _OutlineColor;
struct VertexInput
{
float4 vertex : POSITION;
float3 normal :NORMAL;
};
struct VertexOutput
{
float4 vertex : SV_POSITION;
};
VertexOutput vert(VertexInput v)
{
VertexOutput o = (VertexOutput)0;
// Outline Expansion
v.vertex.xyz += v.normal * _OutlineWidth;
o.vertex = UnityObjectToClipPos(v.vertex);
return o;
}
fixed4 frag(VertexOutput i) : SV_Target
{
return _OutlineColor;
}
ENDCG
}
// Shading Pass
Pass
{
// 裏面をカリングする
Cull Back
// 今まで使用してきたPass
}
}
 レンダリング結果は上図のようになります.球のようなエッジが丸いソフトエッジのオブジェクトはこれできれいにレンダリングされますが,キューブのようなハードエッジのオブジェクトは角部分のアウトラインが切れてしまいます.
レンダリング結果は上図のようになります.球のようなエッジが丸いソフトエッジのオブジェクトはこれできれいにレンダリングされますが,キューブのようなハードエッジのオブジェクトは角部分のアウトラインが切れてしまいます.
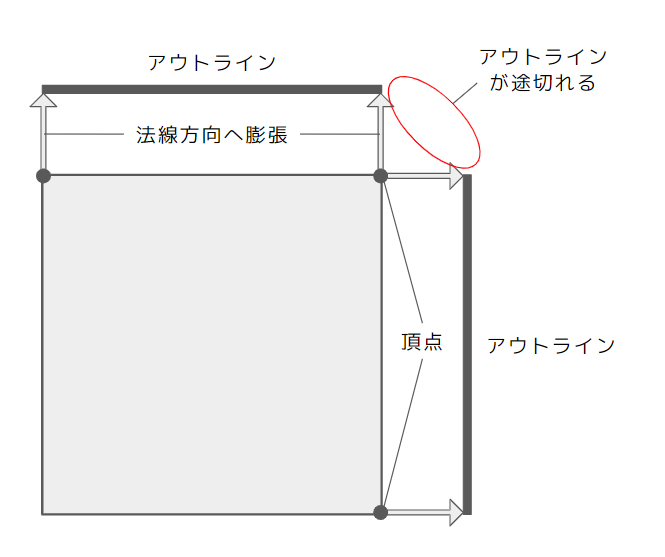
ハードエッジのオブジェクトでも綺麗なアウトラインを描画する方法の1つとして,頂点のオブジェクト座標と法線の内積から,膨張する方向をオブジェクト座標方向/法線方向で切り替えるというものがあります.
オブジェクト座標方向にアウトラインを膨張させるには,以下のような計算式を使用します.
v.vertex.xyz = normalize(v.vertex.xyz) * _OutlineWidth
原理は下図の通りです.

この式を用いた場合のレンダリング結果は以下のようになります.

ここまででみるとオブジェクト座標方向に伸ばしたほうが良いように見えますが,基本的には法線方向にアウトラインを膨張させたほうが見栄えが良いです.ハードエッジ部分だけをオブジェクト座標方向にアウトラインを膨張させるために,内積で切り替えるようにします.
float3 dir = normalize(v.vertex.xyz);
v.vertex.xyz += lerp(v.normal, dir, step(dot(v.normal, dir), _OutlineSmoothThreshold))) * _OutlineWidth;
上記の式でしきい値によってアウトラインの膨張をオブジェクト座標方向か法線方向か切り替えられるようになります.
この特殊な処理もマルチコンパイルして実装しちゃいましょう.
Properties
{
[Header(Outline)]
_OutlineWidth ("Outline Width", Range(0.0, 1.0)) = 0.02
_OutlineColor ("Outline Color", Color) = (0, 0, 0, 1)
[Toggle(USE_OUTLINESMOOTHEXPANSION)] _UseOutlineSmoothExpansion("Use Outline Smooth Expansion", Int) = 0
_OutlineSmoothThreshold ("Outline Smooth Threshold", Range(-1.0, 1.0)) = 0.0
}
SubShader
{
// Outline Pass
Pass
{
Cull Front
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#pragma shader_feature USE_OUTLINESMOOTHEXPANSION
#include "UnityCG.cginc"
float _OutlineWidth;
fixed4 _OutlineColor;
float _OutlineSmoothThreshold;
struct VertexInput
{
float4 vertex : POSITION;
float3 normal :NORMAL;
};
struct VertexOutput
{
float4 vertex : SV_POSITION;
};
VertexOutput vert(VertexInput v)
{
VertexOutput o = (VertexOutput)0;
// Outline Expansion
#ifdef USE_OUTLINESMOOTHEXPANSION
float3 dir = normalize(v.vertex.xyz);
v.vertex.xyz += lerp(v.normal, dir, step(dot(v.normal, dir), _OutlineSmoothThreshold)) * _OutlineWidth;
#else
v.vertex.xyz += v.normal * _OutlineWidth;
#endif
o.vertex = UnityObjectToClipPos(v.vertex);
return o;
}
fixed4 frag(VertexOutput i) : SV_Target
{
return _OutlineColor;
}
ENDCG
}
// Shading Pass
Pass
{
// 今まで使用してきたPass
}
}
シェーディング技法まとめ
これまでいくつかのシェーディング技法を紹介してきました.
・Propertiesによる値のセット
・テクスチャマッピング
・Diffuse
・Specular
・リムライティング
・キューブマップ
・マスク
・On/Off/Blend
・トゥーンレンダリング
・マルチコンパイル
・マルチパス
・アウトライン
シェーダーでは上記以外にも,別のバッファを用いて処理を施したり,モデル側に工夫を仕込んだり,ポストエフェクトをかけたり,分布関数を用いてPBR(Physically-based Rendering)したり,様々な表現ができます.
さいごに
ここまで読んでくださり,ありがとうございます!
「シェーダーに興味あるけどやり方わからん!」という方が「なんとなくわかった」くらいになっていただければ幸いです.
是非自分のプロダクトのクオリティの底上げにシェーダーを利用してみてください.