目的
-
強化学習について概要を理解する
-
迷路課題を用いて実際に強化学習をやってみる
-
ML-Agentsを使ってUnity上で強化学習をやってみる
人工知能・機械学習・強化学習
はじめに、強化学習に関連する用語、人工知能(Artificial Intelligence)、機械学習(Machine Learning)、強化学習(Reinforcement Learning)の意味を簡単に押さえておきます。
まず、人工知能についてですが、この言葉には明確な定義が存在しません。人工知能に関する研究領域はかなり広く、研究者についても様々な立場があるため、特定の定義を置くことが難しいという背景があるようです。ここでは**「人間が知能を使って行うことをコンピュータに模倣させようとする技術」**としておきましょう。
次に、機械学習とは、大量のデータからルールや知識を自ら学習する技術のことを指します。もう少し人工知能との関係を明瞭にする言い方をすれば、「データからその法則性を学習することで、解法が明確でない(人が規則を設計するのが難しい)タスクを遂行するためのモデルを構築すること」となるでしょうか。
重要なのは、機械学習の定義に学習するという文言が含まれることです。一見知的に振る舞うように見えるからといってもそれが全て機械学習であるとは限りません。専門家の知識を人手によってルール化し、そのルールに従って処理するようなシステム(エキスパートシステム)もある種知的に振る舞っているように見えることも多々あります。
機械学習の分類
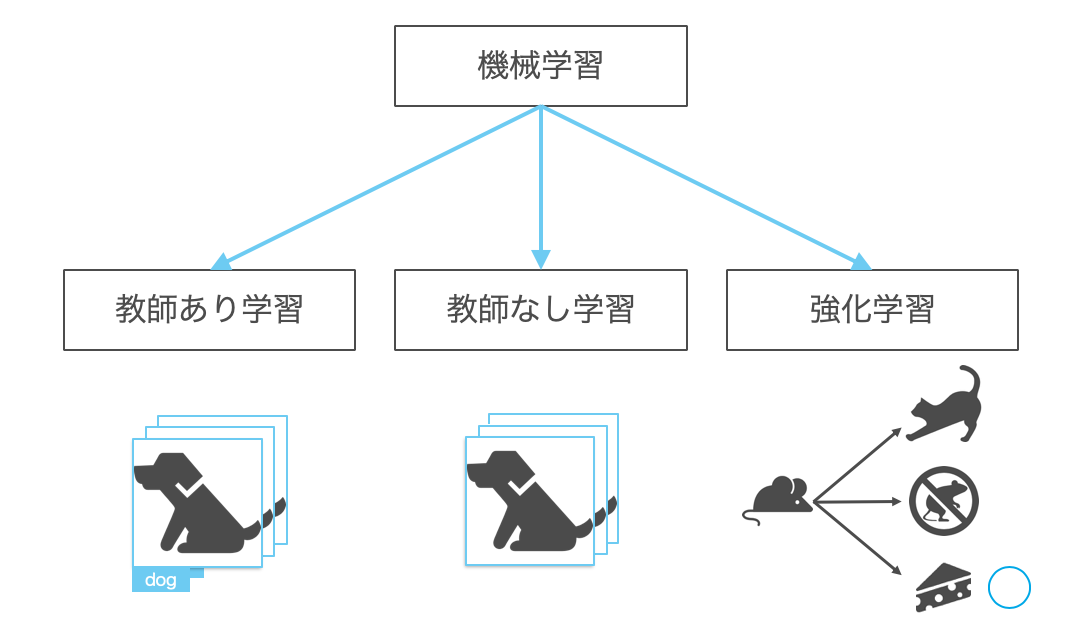
機械学習の手法を「**教師データ(正解ラベル)**がどのように与えられるか」という視点で大まかに分類すると以下のようになります。
まず、教師あり学習と教師なし学習に関してはそのままの意味で、前者は教師データが与えられる手法、後者は教師データが与えられない手法になります。これらの手法とは異なり、強化学習は間接的に教師データが与えられる手法になります。
教師あり学習
売上予測や株価予測のように、入力データと正解の数値の組み合わせを学習し、未知データから数値(連続値)を予測する回帰(Regression)と、画像分類、迷惑メールの判定といった入力データと正解のクラスの組み合わせを学習することで、未知データからクラス(離散値)を予測する分類(Classification)の2種類に大別されます。
教師なし学習
教師なし学習はデータ自身の構造や分布をモデル化することで、データの性質を知る手法です。代表的な手法としてデータを同じような性質を持ついくつかのグループに分けるクラスタリング(Clustering)というものがあります。例えば、商品の購入状況から顧客をグループ化し、それぞれのグループに適したマーケティング手段を用いることでマーケティング効果を上げるといった使い方もできます。
他にも、
- ソーシャルネットワーク分析(SNS上で人のつながりを分析する)
- アソシエーション分析(顧客ごとに異なったオススメ商品を紹介する)
も教師なし学習の一種です。
強化学習
間接的に教師データが与えられるというのは、個々の決定に対して明確な正解は与えられないが、連続した決定の結果に対して(形を変えた)教師データが遅れて与えられるということです。例えば、コンピュータ将棋のソフトウェアを考えたとき、各盤面でどの駒をどのように動かせばよいかという正解は与えられませんが、最終的に試合に勝ったか負けたかなどの結果は分かります。この、「ゲームに勝つ」というような**「長期的な価値」を最大化するように試行錯誤を繰り返し行動を学習する**のが強化学習なのです。
**深層学習**
強化学習
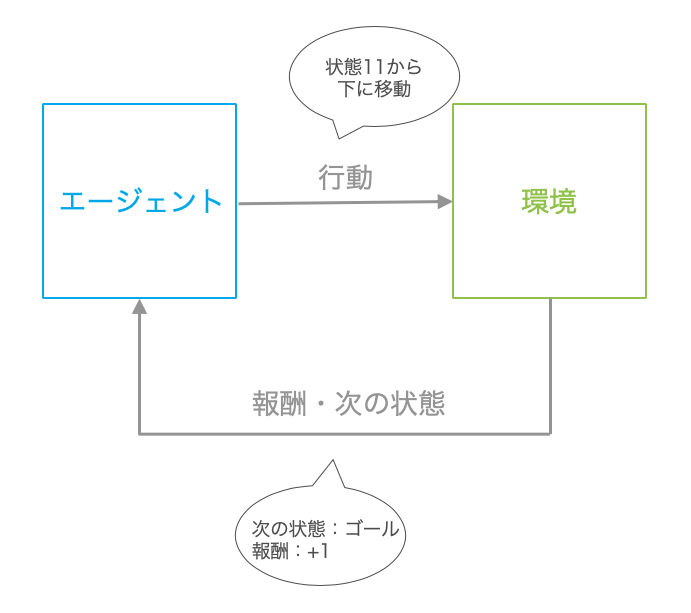
強化学習の概要とよく使われる用語を整理するために、迷路を解くための強化学習を考えます。迷路内をエージェントが移動してゴールを目指し、エージェントがゴールに辿り着くと報酬が与えられるという設定です。このとき、ある状態からどのように行動するのかを定めたルールを方策といいます。ここで、状態とはエージェントがいる位置になり、行動は上下左右のいずれかに進むことに当たります。さらに、今回でいう迷路の構造や設定全体のことを環境といいます。
**「環境」についての補足**

| 用語 | 説明 |
|---|---|
| エージェント(agent) | 行動する主体 |
| 環境(environment) | エージェントが行動する対象 |
| 報酬(reward) | エージェントの行動の結果として獲得できる報酬 |
| 方策(policy) | 行動を決めるルール |
方策勾配に基づくアルゴリズム
強化学習のアルゴリズムの一手法として方策勾配に基づくものを紹介します。
方策勾配に基づく強化学習を簡潔に述べると、**「方策を確率モデルで表現し、そのパラメータを学習する」**ということになりますが、文章を見ていても分かりづらいと思うので先程の迷路の設定で例を考えていきます。
まず、今回エージェントの行動を決めるルールである方策$\pi_{\theta}$を、ある状態から上下左右のいずれかに進むかの確率とします。例えば、迷路上の状態 s0(スタート)では、右(s1)、下(s4)の2方向に進むことができますが、初めのうちは、エージェントはどちらに進めばよいか分からないので、$\frac{1}{2}$の確率で右か下に進むことになります。ただし、迷路の構造を分かっている我々からすれば、下に進んでもゴールにはたどりつけないので、状態 s0 では右に進む確率の方が大きくなってくれると嬉しいです。このように、ゴールにより近づく方向に進む確率が大きくなるように何度も迷路を解くことで訓練していきます。
方策(各状態で上下左右に進む確率)を行列で表すと次のようになります。壁がある方向には進めないので確率は0とし、行は状態(s0〜s14)を、列は方向(↑、→、↓、←)を示します。例えば s1(2行目) は、↑以外の3方向(→、↓、←)に等しく0.333の確率で進むようになっています。
[[0. 0.5 0.5 0. ]
[0. 0.333 0.333 0.333]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[0.5 0. 0.5 0. ]
[0.333 0.333 0.333 0. ]
[0. 0.5 0. 0.5 ]
[0.5 0. 0. 0.5 ]
[0.5 0. 0.5 0. ]
[0.5 0.5 0. 0. ]
[0. 0.5 0. 0.5 ]
[0. 0. 0.5 0.5 ]
[0.5 0.5 0. 0. ]
[0. 0.5 0. 0.5 ]
[0. 0. 0. 1. ]]
この方策で迷路問題を解くと、次のようになります。当然ランダムに移動していくようなものなので、最短ルート s0(Start) → s1 ↓ s5 ↓ s9 → s10 → s11 → s15(Goal) **(6step)**からはほど遠く、同じところを何度も行ったり来たりしています。
[[0, '→'], [1, '←'], [0, '↓'], [4, '↓'], [8, '↑'], [4, '↑'], [0, '↓'], [4, '↑'], [0, '→'],
[1, '↓'], [5, '→'], [6, '→'], [7, '↑'], [3, '↓'], [7, '↑'], [3, '↓'], [7, '←'], [6, '→'],
[7, '←'], [6, '→'], [7, '←'], [6, '←'], [5, '→'], [6, '→'], [7, '←'], [6, '←'], [5, '↓'],
[9, '↑'], [5, '↓'], [9, '↑'], [5, '↓'], [9, '↑'], [5, '→'], [6, '→'], [7, '←'], [6, '→'],
[7, '←'], [6, '←'], [5, '↓'], [9, '→'], [10, '→'], [11, '↓'], [15, 'np.nan']]
steps : 42
エージェントが最短ルートで迷路をクリアすることができるよう、方策を少しずつ更新していくのですが、実際には、その元になるパラメータ$\theta$を更新していきます。パラメータと言っても今回はかなりシンプルなもので、下のように、進める方向に対しては1、進めない方向(壁)に対してはnp.nanとした行列とします。
**np.nan**
今回、進めない方向なので0とすればよいのでは?と、疑問かもしれませんが、この壁に進む方向の確率は方策の更新とは無関係に常に0とする必要がありますが、0としていると更新されてしまうかもしれないので、np.nanとしています。np.nanに対しては演算を施してもnp.nanになるので、更新されません。
theta_0 = np.array([[np.nan, 1, 1, np.nan], # s0
[np.nan, 1, 1, 1], # s1
[np.nan, np.nan, np.nan, 1], # s2
[np.nan, np.nan, 1, np.nan], # s3
[1, np.nan, 1, np.nan], # s4
[1, 1, 1, np.nan], # s5
[np.nan, 1, np.nan, 1], # s6
[1, np.nan, np.nan, 1], # s7
[1, np.nan, 1, np.nan], # s8
[1, 1, np.nan, np.nan], # s9
[np.nan, 1, np.nan, 1], # s10
[np.nan, np.nan, 1, 1], # s11
[1, 1, np.nan, np.nan], # s12
[np.nan, 1, np.nan, 1], # s13
[np.nan, np.nan, np.nan, 1], # s14
])
このパラメータを下のようにして単純に割合を求め、先程示したような方策とします。
def policy(theta):
[m, n] = theta.shape
pi = np.zeros((m, n))
for i in range(0, m):
pi[i, :] = theta[i, :] / np.nansum(theta[i, :])
pi = np.nan_to_num(pi)
return pi
それでは、下のように方策を更新していきます。
stop_epsilon = 10**-4
theta = theta_0
pi = pi_0
is_continue = True
while is_continue:
sa_history = solve(pi) #迷路を解く
new_theta = update_theta(theta, pi, sa_history) #パラメータの更新
new_pi = policy(new_theta) #方策の更新(パラメータ -> 方策)
if np.sum(np.abs(new_pi - pi)) < stop_epsil
is_continue = False
else:
theta = new_theta
pi = new_pi
迷路を解く関数
def solve(pi):
s = 0 # スタート
sa_history = [[0, np.nan]]
while (1):
[action, next_s] = action_and_next_s(pi, s)
sa_history[-1][1] = action
sa_history.append([next_s, np.nan])
if next_s == 15: #ゴール
break
else:
s = next_s
return sa_history
パラメータの更新
def update_theta(theta, pi, sa_history):
eta = 0.1 # 学習率
T = len(sa_history) - 1 # ゴールまでの総ステップ数
[m, n] = theta.shape
delta_theta = theta.copy()
for i in range(0, m):
for j in range(0, n):
if not(np.isnan(theta[i, j])):
SA_i = [SA for SA in sa_history if SA[0] == i]
SA_ij = [SA for SA in sa_history if SA == [i, j]]
N_i = len(SA_i)
N_ij = len(SA_ij)
delta_theta[i, j] = (N_ij - pi[i, j] * N_i) / T
new_theta = theta + eta * delta_theta
return new_theta
学習が進んでいくと、段々と最短ルートに近いステップ数(6step)でゴールすることができるようになっています。
Update amount0.0133 Steps 66
Update amount0.0161 Steps 62
Update amount0.0104 Steps 94
Update amount0.0105 Steps 78
Update amount0.0097 Steps 252
Update amount0.0100 Steps 74
~~~~~~~~~~~~省略~~~~~~~~~~~~~~
Update amount0.0041 Steps 6
Update amount0.0131 Steps 10
Update amount0.0036 Steps 6
Update amount0.0144 Steps 8
Update amount0.0036 Steps 6
Update amount0.0036 Steps 6
ゴールまでにかかったステップ数の遷移を図に表すと下のようになります。しっかり減っていっているのが確認できます。
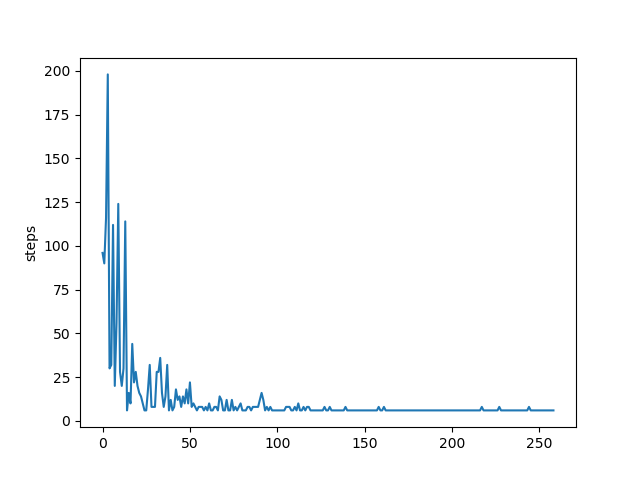
最終的な方策と、その方策で迷路を解いた結果は次のようになります。例えばs11(下から4段目)は↓に進めばすぐにゴールですが、↓に進む確率が1で他が0となっており、うまく方策が学習できています。また、その方策で迷路を解くとs0(Start) → s1 ↓ s5 ↓ s9 → s10 → s11 → s15(Goal) **(6step)**の最短ルートでゴールできていることがわかります。
[[0. 1. 0. 0. ]
[0. 0. 0.991 0.008]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[0.631 0. 0.369 0. ]
[0. 0. 1. 0. ]
[0. 0.299 0. 0.701]
[0.468 0. 0. 0.532]
[0.574 0. 0.426 0. ]
[0. 1. 0. 0. ]
[0. 1. 0. 0. ]
[0. 0. 1. 0. ]
[0.523 0.477 0. 0. ]
[0. 0.499 0. 0.501]
[0. 0. 0. 1. ]]
[[0, '→'], [1, '↓'], [5, '↓'], [9, '→'], [10, '→'], [11, '↓'], [15, 'np.nan']]
steps : 6
今回使用した、ソースコードは以下に置いてあります。
https://github.com/casp39/rl_maze
ML-Agents
Unity上で、強化学習、模倣学習、その他機械学習が行えるプラグインであるML-Agentsの導入をし、サンプルのゲームを動かしてみます。
ML-Agents 環境構築
Unityのインストール
Unityをダウンロードし、インストールします。
ML-Agents は Unity2017.4 以降のバージョンにしか対応していません。
今回は、Unity2017.4を使用していきます。
ML-Agentsリポジトリをクローン
適当なディレクトリにリポジトリをクローンします。
git clone https://github.com/Unity-Technologies/ml-agents.git
Python と ML-Agentsのインストール
ML-Agentsのインストールが終わったらPythonと、周辺ライブラリを入れます。
まず、Anacondaをダウンロードし、インストールします。
Anaconda
Anacondaのインストールが終わったらML-Agents用の仮想環境を用意します。
conda update -n base conda
conda create --name mlagents python=3.6
source activate mlagents
pip install mlagents
Tensorflowをインストール
※ 現在ML-Agentsの最新verはTensorFlow1.15.0と互換がないのでTensorFlow1.15.0をインストールします。
pip install tensorflow==1.14
UnityでML-Agentsをセットアップ
1. Unityを起動する
2. Openボタン を選択し、ml-agents/UnitySDK/ を開く
3. Edit > Project Settings > Player
Other Settingsを変更する
| Scripting Runtime Version | Experimental (.NET 4.6 Equivalent or .NET 4.x Equivalent) |
|---|---|
| Scripting Defined Symbols | ENABLE_TENSORFLOW |
参考画像
4. File > Save Project
サンプルの学習環境(3DBall)
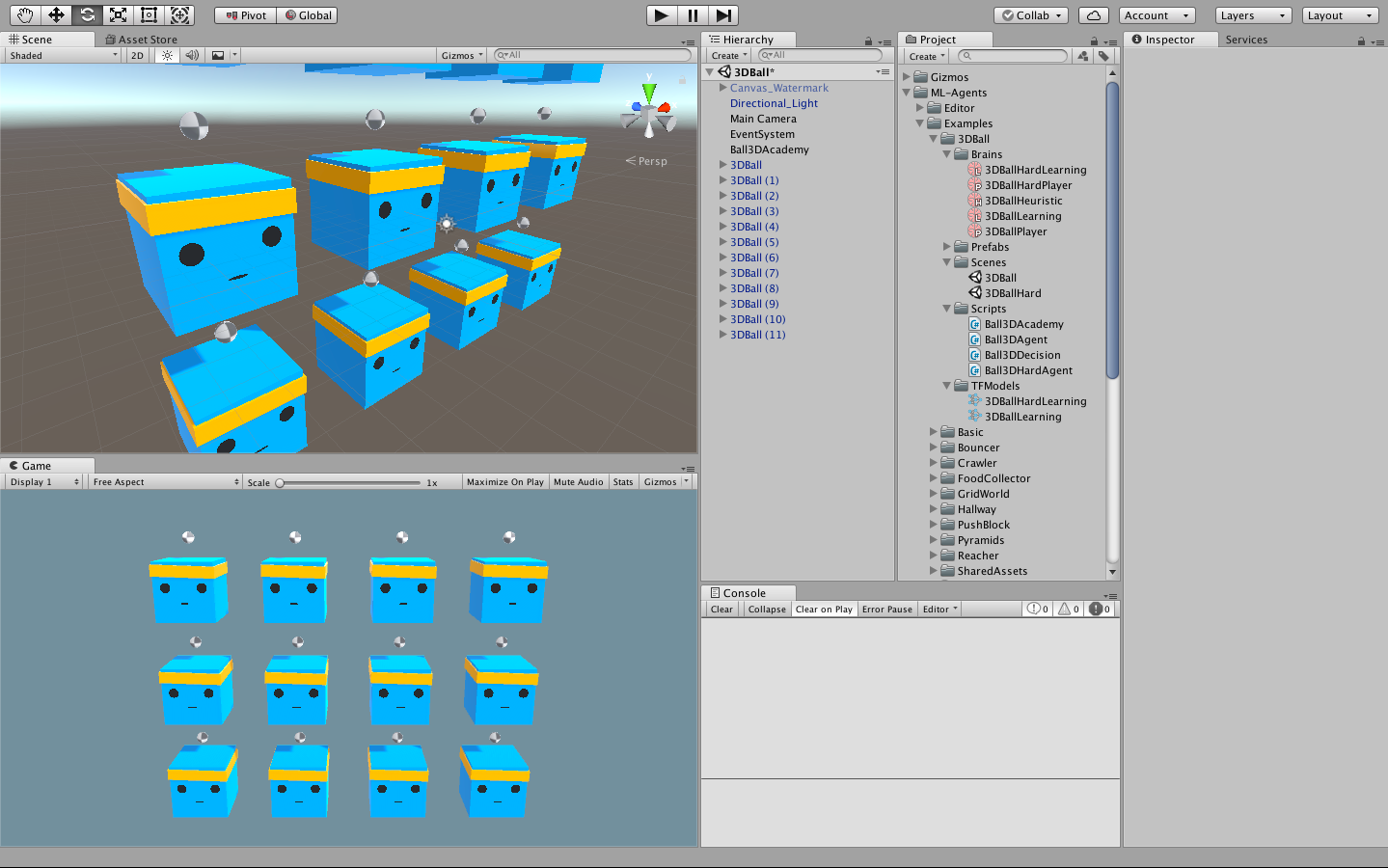
Project window で Assets/ML-Agents/Examples/3DBall フォルダの中の 3DBall シーンファイル を開きます。今回扱うサンプルは箱の上に落下してくるボールを落とさないように箱を動かしてバランスをとるというようなものです。
ML-Agentsの用語整理
サンプルの学習を行う前に、ML-Agentsで重要になる用語を整理しておきます。
Agent
学習環境内で行動するオブジェクトのことをAgentと呼びます。今回の場合、ボールを落とさないようにボールを制御する箱がAgentに当たります。
Brain
BrainはAgentの観測した状態と報酬を用いてAgentの行動を決定します。今回Agentが観測できるのは、現在のAgent(箱)の回転角度とボールの位置・速度です。報酬は各時刻ごとににボールが箱の上にあると+0.1、ボールを箱の上から落としすと-1.0の報酬が得られる設定になっています。これらの状態と報酬を考慮しBrainが次のAgentの行動を決定します。
Academy
Academyは学習環境を管理するオブジェクトです。トレーニング1回分のことを1 エピソード と呼びますが、何エピソード分すなわち何回分トレーニングを行うかといったことや、学習環境の初期値の設定、レンダリング(解像度等)の設定などを行います。
強化学習によるトレーニング
準備
-
まず、AgentにBrainを割り当てます。
Prefabs>3DBall>AgentのBall 3D Agent (Script)コンポーネントのBrainプロパティにAssets>ML-Agents>Examples>3DBall>Brains>3DBallLearningをドラッグします。 -
次に、Academyの設定を行います。Hierarchyウィンドウで、Ball3DAcademyを選択します。Agentと同じようにして、
Ball 3D Academy (Script)コンポーネントの'''Brain'''プロパティにAssets>ML-Agents>Examples>3DBall>Brains>3DBallLearningをドラッグします。また、学習の際にはControlプロパティにチェックを入れる必要があります。
学習
- 再度ターミナルを開き ML-Agentsリポジトリ をクローンしたディレクトリへ移動し、次を実行します。
mlagents-learn config/trainer_config.yaml --run-id=firstRun --train
オプションの--trainは学習を実行することを表しています。(推論時は不要)
- Start training by pressing the Play button in the Unity Editor. のメッセージが表示されるのを確認後 Unity に戻り、 再生ボタン を押す
すると、学習が始まります。初めのうちは板はボールをボロボロ落としています(左図)が、学習が進んでくるとなかなかボールを落とさなくなってくる(右図)のが分かります。
| 1000ステップ後 | 10000ステップ後 |
|---|---|
 |
 |
ターミナルにはもう少し詳しい情報が表示されています。少し確認してみましょう。
情報全体
INFO:mlagents.envs:Hyperparameters for the PPO Trainer of brain Ball3DBrain:
batch_size: 64
beta: 0.001
buffer_size: 12000
epsilon: 0.2
gamma: 0.995
hidden_units: 128
lambd: 0.99
learning_rate: 0.0003
max_steps: 5.0e4
normalize: True
num_epoch: 3
num_layers: 2
time_horizon: 1000
sequence_length: 64
summary_freq: 1000
use_recurrent: False
graph_scope:
summary_path: ./summaries/firstRun-0
memory_size: 256
use_curiosity: False
curiosity_strength: 0.01
curiosity_enc_size: 128
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 1000. Mean Reward: 1.180. Std of Reward: 0.684. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 2000. Mean Reward: 1.328. Std of Reward: 0.755. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 3000. Mean Reward: 1.664. Std of Reward: 0.970. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 4000. Mean Reward: 2.355. Std of Reward: 1.631. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 5000. Mean Reward: 3.706. Std of Reward: 3.188. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 6000. Mean Reward: 6.255. Std of Reward: 6.104. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 7000. Mean Reward: 9.339. Std of Reward: 8.283. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 8000. Mean Reward: 12.943. Std of Reward: 11.746. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 9000. Mean Reward: 22.260. Std of Reward: 20.912. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 10000. Mean Reward: 39.189. Std of Reward: 29.556. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 11000. Mean Reward: 48.570. Std of Reward: 33.496. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 12000. Mean Reward: 66.494. Std of Reward: 32.763. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 13000. Mean Reward: 81.663. Std of Reward: 33.271. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 14000. Mean Reward: 88.731. Std of Reward: 21.941. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 15000. Mean Reward: 95.200. Std of Reward: 15.920. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 16000. Mean Reward: 91.186. Std of Reward: 25.583. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 17000. Mean Reward: 86.814. Std of Reward: 32.300. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 18000. Mean Reward: 85.985. Std of Reward: 20.061. Training.
INFO:mlagents.trainers: firstRun-0: Ball3DBrain: Step: 19000. Mean Reward: 100.000. Std of Reward: 0.000. Training.
^C--------------------------Now saving model-------------------------
INFO:mlagents.envs:Learning was interrupted. Please wait while the graph is generated.
まず、以下の部分では強化学習のアルゴリズムとしてPPO(Proximal Policy Optimization)を用いていることを表しています。これは、先程説明した方策勾配法ベースの手法で、実装が比較的簡単なアルゴリズムとして注目されています。
INFO:mlagents.envs:Hyperparameters for the PPO Trainer of brain Ball3DBrain:
次に、ステップごとの平均報酬が表されていますが、段々と多くの報酬が貰えるようになっているので学習が上手くいっていることが分かります。
INFO: Step: 1000. Mean Reward: 1.180.
INFO: Step: 2000. Mean Reward: 1.328.
INFO: Step: 3000. Mean Reward: 1.664.
INFO: Step: 4000. Mean Reward: 2.355.
INFO: Step: 5000. Mean Reward: 3.706.
INFO: Step: 6000. Mean Reward: 6.255.
INFO: Step: 7000. Mean Reward: 9.339.
INFO: Step: 8000. Mean Reward: 12.943.
INFO: Step: 9000. Mean Reward: 22.260.
INFO: Step: 10000. Mean Reward: 39.189.
INFO: Step: 11000. Mean Reward: 48.570.
INFO: Step: 12000. Mean Reward: 66.494.
INFO: Step: 13000. Mean Reward: 81.663.
INFO: Step: 14000. Mean Reward: 88.731.
INFO: Step: 15000. Mean Reward: 95.200.
INFO: Step: 16000. Mean Reward: 91.186.
INFO: Step: 17000. Mean Reward: 86.814.
INFO: Step: 18000. Mean Reward: 85.985.
INFO: Step: 19000. Mean Reward: 100.000.
ちなみに、途中で学習をやめるにはCtrl + Cを押します。
推論
さきほど学習したモデルはmodels/firstRun-0/3DBallLearning.nnにあります。これをProject windowのML-Agents/Examples/3DBall/TFModels/にドラッグします。
参考画像
※ デフォルトでTFModels内に3DBallLearning.nnがある場合は、先にそれを削除してからモデルをドラッグしましょう。
-
推論の際は
Ball3DAcademyのControlプロパティのチェックをはずす必要があります。 -
Assets>ML-Agents>Examples>3DBall>Brains>3DBallLearningのModelにさきほど学習したモデルをドラッグします。

- 再生ボタンを押すと推論が始まります。
板がボールを落とさないように制御できていることが分かります。

ML-Agentsには他にも様々なサンプルがあるので、試してみると良いでしょう。
| tennis | soccer | pyramids |
|---|---|---|
 |
 |
 |
補足
人工知能の定義
松尾豊「人工知能は人間を超えるか」(KADOKAWA)に国内の研究者複数人の考える人工知能の定義がまとめられています。
人工知能の分類
人工知能は**「汎用人工知能」と「特化型人工知能」**の2つに分類することができます。前者は様々な一般的な状況に対応し、自律的な思考・検討を行なうことができる人工知能のことを指します。ドラえもんをイメージするとわかりやすいでしょう。後者は自動運転や、画像識別、囲碁・将棋など特定の領域に対して専門化した能力を持つ人工知能です。今回の定義は後者寄りですが、実際昨今の人工知能関連の研究の多くは後者にあたります。
中間的学習
機械学習を教師データの与えられ方を基準に、教師あり学習、教師なし学習、強化学習の3種類に分類しましたが、この他に少量のラベル(正解)付きデータと大量のラベル無しデータを用いて学習する半教師あり学習というものもあります。この半教師あり学習と強化学習をまとめて中間的学習とよぶ文献もあります。
参考文献
強化学習
[1] 牧野 貴樹ほか『これからの強化学習』(森北出版、2016)
[2] Richard S.Sutton and Andrew G.Barto(三上 貞芳、 皆川 雅章訳)『強化学習』(森北出版、2006)
[3] 小川雄太郎『つくりながら学ぶ! 深層強化学習』(マイナビ出版、2018)
ML-Agents
[4] 「Learn how to use Unity Machine Learning Agents - Unity」
〔 https://unity3d.com/jp/how-to/unity-machine-learning-agents 〕
(最終検索日 : 2018 年 12 月 9 日)
[5] 布留川 英一『Unityではじめる機械学習・強化学習 Unity ML-Agents実践ゲームプログラミング』(ボーンデジタル、2018)
Proximal Policy Optimization
[6] J Schulman, F Wolski, P Dhariwal, A Radford and O Klimov. “Proximal Policy Optimization Algorithms”. In: arXiv preprint arXiv:1707.06347 (2017).