アフィン変換の真価を知ったら実はかなり強かった、という話。我々はアフィン変換の本当のすごさを知らない。
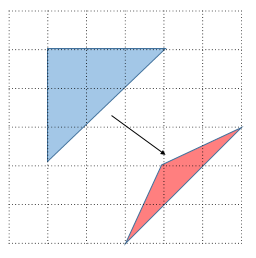
サンプル
非常に複雑な変換に見えますが、たった1回のアフィン変換でやっています。この記事の処理を組み合わせていけばこの処理が実装できます。

アフィン変換
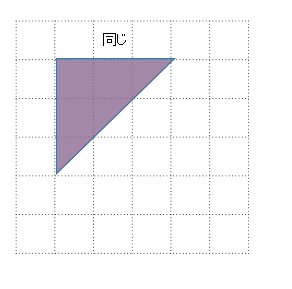
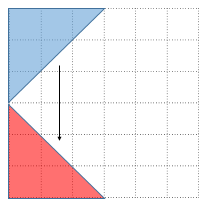
平面のアフィン変換とは三角形の移動(写像)を与えることで決まる変換のこと(証明は末尾参照)。
画像の回転処理にアフィン変換がよく用いられますが、アフィン変換≠回転です。アフィン変換はもっと広く処理ができますし、回転処理はその一部です。最初に回転を考えると理解しにくくなります。
OpenCVでの実装
今回は数学的にあまり突っ込まずに「PythonのOpenCVで自分で実装できればOK」レベルを目指します。OpenCVでは次のようにアフィン変換を行います。
import cv2
af = cv2.getAffineTransform(src, dest)
converted = cv2.warpAffine(image, af, (size_x, size_y))
src, destには3点分のxy座標をnp.float32型で(3,2)のshapeのNumpy配列で与えます。imageには画像のNumpy配列、**(size_x, size_y)**は出力のサイズを表します。
また回転操作では変換後の座標をいちいち三角関数で計算するのが面倒なので、getRotationMatrix2Dという専用の関数が用意されています。やっていることはgetAffineTransformと同じです。
具体例
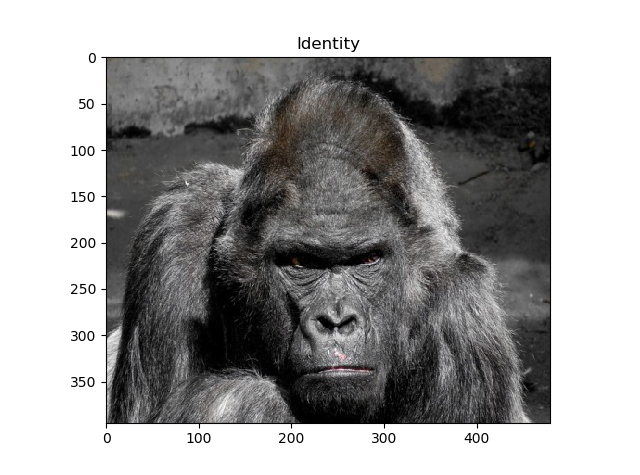
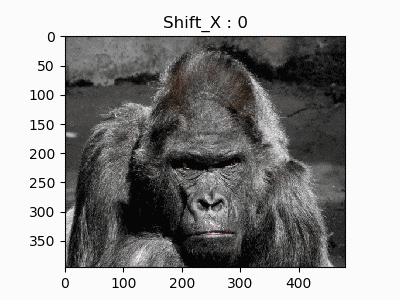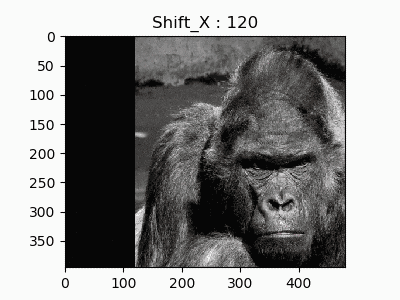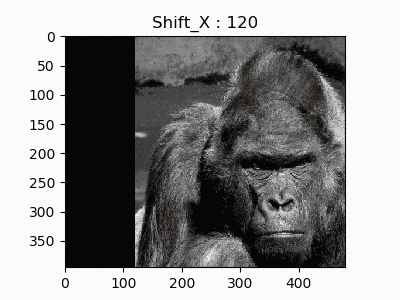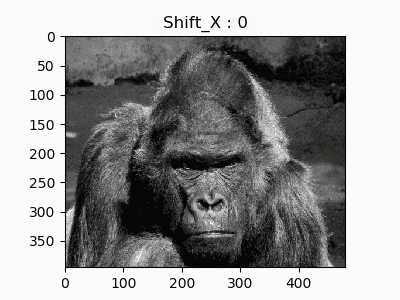
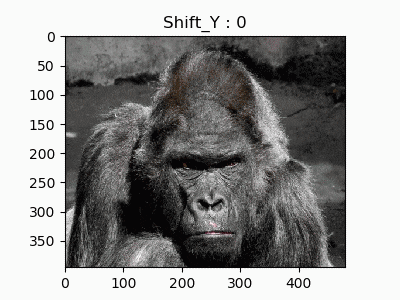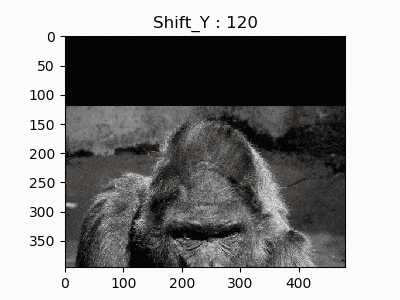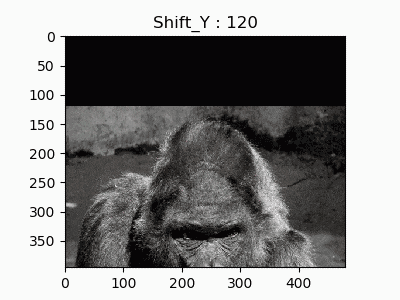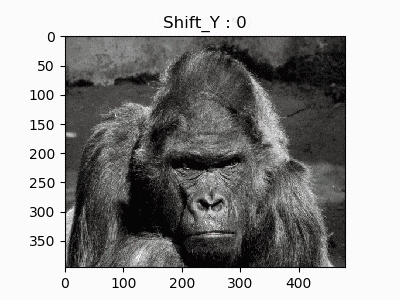
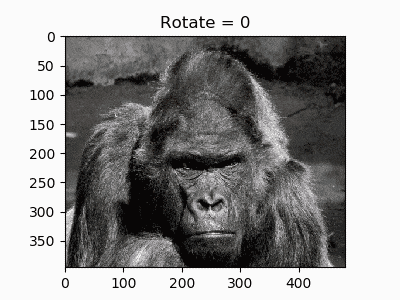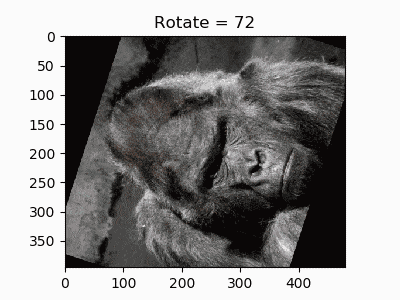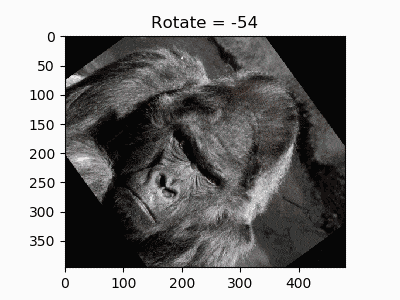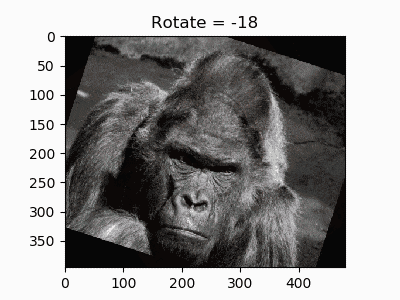
この画像を変換していきます。「gorilla.jpg」とします。
移動
1. 恒等変換
import cv2
import matplotlib.pyplot as plt
import numpy as np
def identity(image):
h, w = image.shape[:2]
src = np.array([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0]], np.float32)
affine = cv2.getAffineTransform(src, src)
return cv2.warpAffine(image, affine, (w, h))
if __name__ == "__main__":
image = cv2.imread("gorilla.jpg")[:,:,::-1]
converted = identity(image)
plt.imshow(converted)
plt.title("Identity")
plt.show()
これだって立派なアフィン変換です。次回移行importと「if name==」以下を省略して書きます。
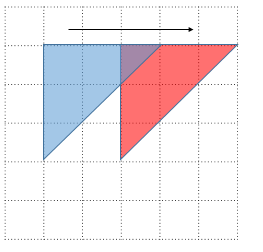
2.水平移動
単に横にスライドする操作もアフィン変換で書けます
def shift_x(image, shift):
h, w = image.shape[:2]
src = np.array([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0]], np.float32)
dest = src.copy()
dest[:,0] += shift # シフトするピクセル値
affine = cv2.getAffineTransform(src, dest)
return cv2.warpAffine(image, affine, (w, h))
3.垂直移動
縦へのスライドもできます。
def shift_y(image, shift):
h, w = image.shape[:2]
src = np.array([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0]], np.float32)
dest = src.copy()
dest[:,1] += shift # シフトするピクセル値
affine = cv2.getAffineTransform(src, dest)
return cv2.warpAffine(image, affine, (w, h))
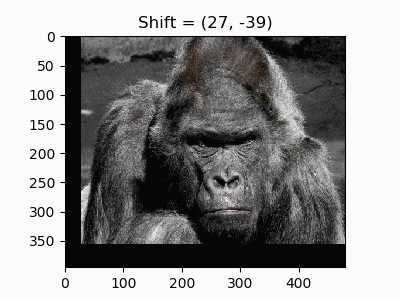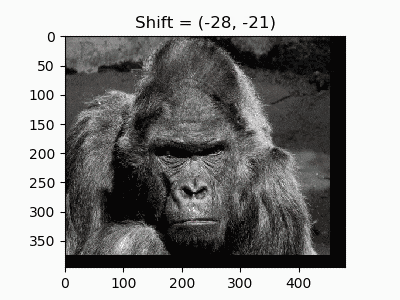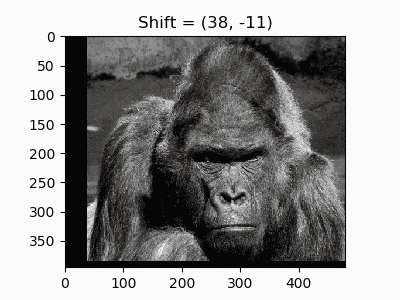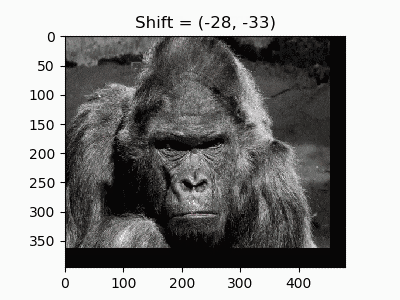
4. ランダムシフト
水平と垂直移動を組み合わせて任意の座標移動ができます。ディープラーニングのData Augmentationで使う「ランダムクロップ」もアフィン変換で再現できます。
def random_shift(image, shifts):
h, w = image.shape[:2]
src = np.array([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0]], np.float32)
dest = src + shifts.reshape(1,-1).astype(np.float32)
affine = cv2.getAffineTransform(src, dest)
return cv2.warpAffine(image, affine, (w, h))
移動元、移動先の座標はnp.float32にしないと怒られるので注意しましょう。
拡大・縮小(Scale)
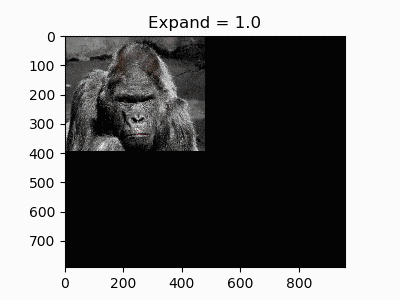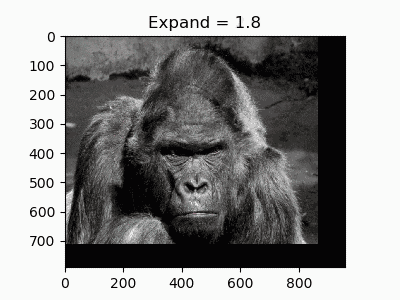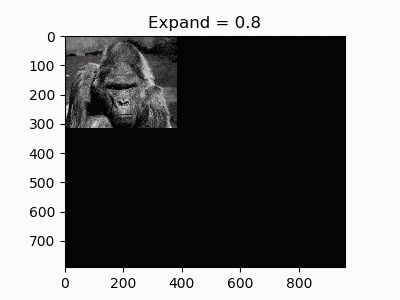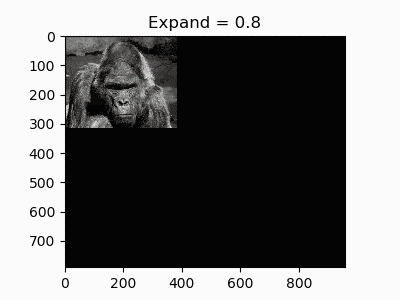
5.拡大・縮小
移動系では移動先の座標を足し算で計算していましたが、これを掛け算にかえると拡大・縮小になります。
def expand(image, ratio):
h, w = image.shape[:2]
src = np.array([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0]], np.float32)
dest = src * ratio
affine = cv2.getAffineTransform(src, dest)
return cv2.warpAffine(image, affine, (2*w, 2*h), cv2.INTER_LANCZOS4) # 補間法も指定できる
拡大縮小に限った話ではありませんが、補間法も通常のresizeと同様に指定できます。今回は最高品質のLANCZOS法を使ってみました。デフォルトだと線形補間(INTER_LINEAR)になります。
せん断(Shear)
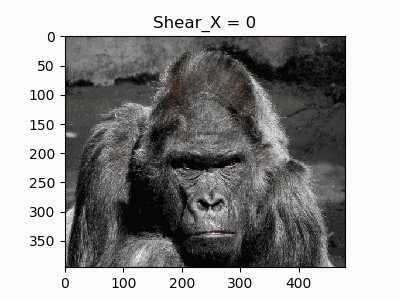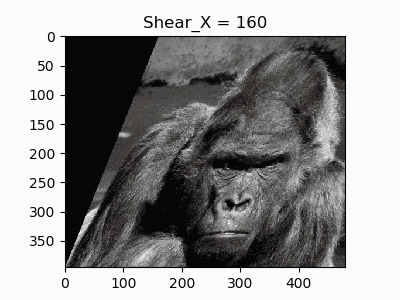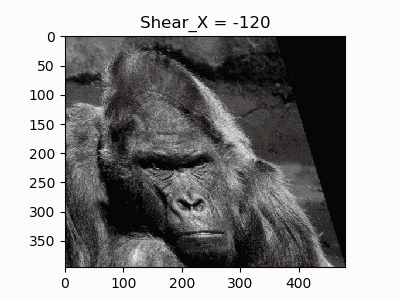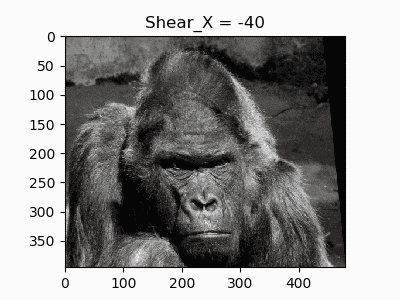
6.水平方向のせん断
平行四辺形型の変換をするのを**せん断(Shear)**といいます。
横方向の歪みを作ります。考え方は水平移動と同じで$x$座標を足していくのですが、$y$座標ごとに足していく$x$を少しずつ変えていくと「せん断」の変形になります。
def shear_X(image, shear):
h, w = image.shape[:2]
src = np.array([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0]], np.float32)
dest = src.copy()
dest[:,0] += (shear / h * (h - src[:,1])).astype(np.float32)
affine = cv2.getAffineTransform(src, dest)
return cv2.warpAffine(image, affine, (w, h))
平面方向の回転は一切やっていないのに注意してください。
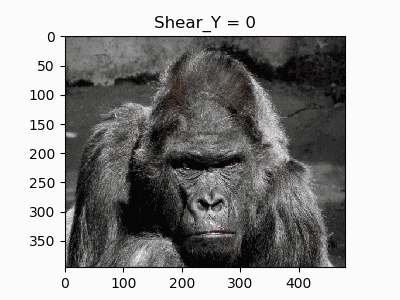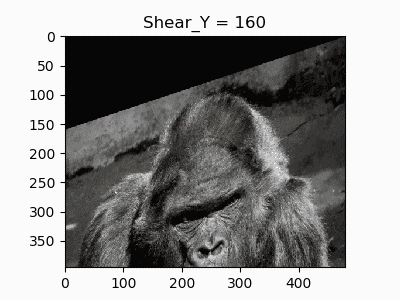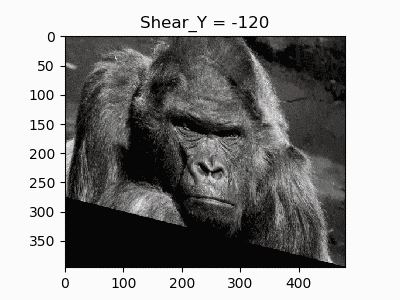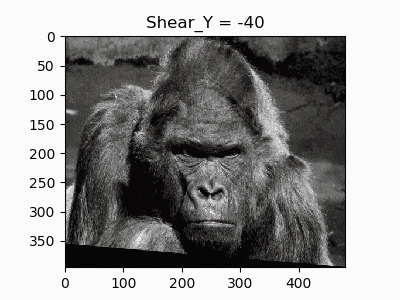
7. 垂直方向のせん断
同様に垂直方向のせん断を行います。
def shear_Y(image, shear):
h, w = image.shape[:2]
src = np.array([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0]], np.float32)
dest = src.copy()
dest[:,1] += (shear / w * (w - src[:,0])).astype(np.float32)
affine = cv2.getAffineTransform(src, dest)
return cv2.warpAffine(image, affine, (w, h))
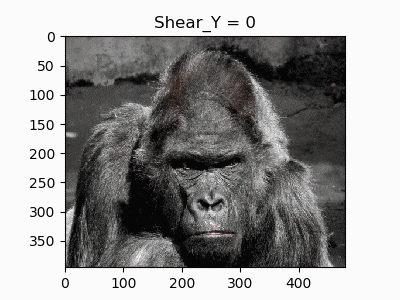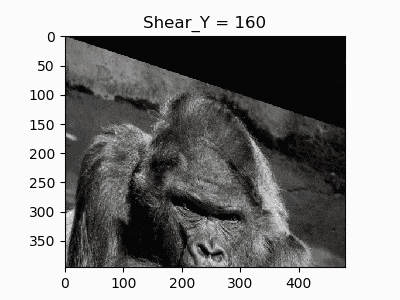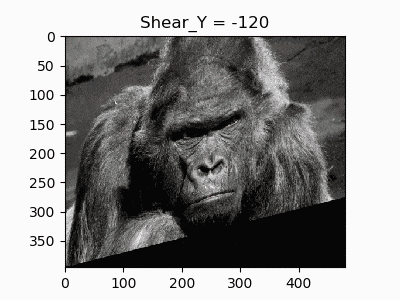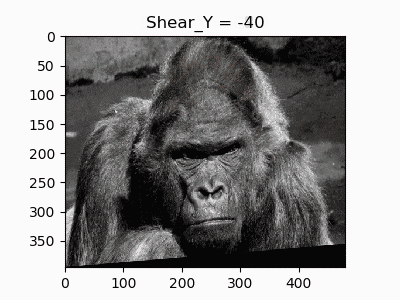
8.垂直方向のせん断(起点違い)
せん断の起点を右上ではなく左上においた変換です。
def shear_Y(image, shear):
h, w = image.shape[:2]
src = np.array([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0]], np.float32)
dest = src.copy()
dest[:,1] += (shear / w * src[:,0]).astype(np.float32)
affine = cv2.getAffineTransform(src, dest)
return cv2.warpAffine(image, affine, (w, h))
反転(Flip)
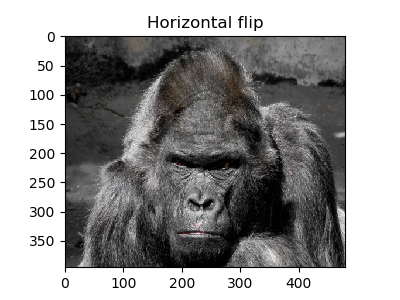
9.水平反転
座標を水平方向に反転させるように定義すれば水平反転になります。これもアフィン変換で定義できます。
def horizontal_flip(image):
h, w = image.shape[:2]
src = np.array([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0]], np.float32)
dest = src.copy()
dest[:,0] = w - src[:,0]
affine = cv2.getAffineTransform(src, dest)
return cv2.warpAffine(image, affine, (w, h))
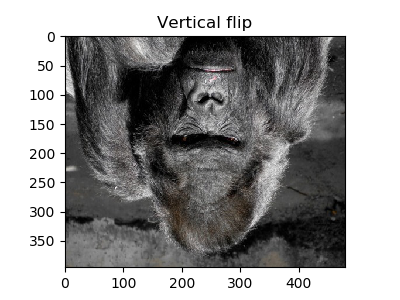
10. 垂直反転
水平反転の軸を変えると垂直反転になります。
def vertical_flip(image):
h, w = image.shape[:2]
src = np.array([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0]], np.float32)
dest = src.copy()
dest[:,1] = h - src[:,1]
affine = cv2.getAffineTransform(src, dest)
return cv2.warpAffine(image, affine, (w, h))
アフィン変換の合成とすごさ
ここまでNumpyでも書けるような処理をアフィン変換で書いてきて、「正直Numpyでもいいんじゃないの?」と思ったかもしれません。しかし、アフィン変換で書ける処理をすべてアフィン変換で書いておくとメリットがあります。その動機づけをしておきます。
アフィン変換の合成=行列の積
$n$個のアフィン変換の行列が3×3行列で$A_1, A_2, \cdots, A_n$で表される時、$A_1\to A_2\to\cdots\to A_n$という合成のアフィン変換は、
$$A_nA_{n-1}\cdots A_2A_1\tag{1}$$
という行列の積で与えられます。まず「アフィン変換の行列とはなんぞ」ということですが、アフィン変換とは以下の式で各点の変換を行うことです。
\begin{cases}
x' = ax+by+x_0 \\
y' = cx+dy+y_0
\end{cases}\tag{2}
これは行列表記をすれば2×3行列で表すことができます。ただし、2×3行列はxy座標の$(2,1)$行列と積を取ることができないので、アフィン変換の行列を3×3行列、xy座標に意味のない1の項をつけて$(3,1)$行列にします。$A_n$の変換は、
\begin{align}
A_n &= \begin{bmatrix}
a_n & b_n & x_{0,n} \\
c_n & d_n & y_{0,n} \\
0 & 0 & 1
\end{bmatrix} \\
\begin{bmatrix}
x' \\ y' \\ 1
\end{bmatrix} &=
\begin{bmatrix}
a_n & b_n & x_{0,n} \\
c_n & d_n & y_{0,n} \\
0 & 0 & 1
\end{bmatrix}\begin{bmatrix}
x \\ y \\ 1
\end{bmatrix}
\end{align} \tag{3}
と表されます。これは(2)式と等価です。なぜなら3行目の値は常に1になるからです。コードで確認してみましょう。例えば以下は「x方向に2倍の拡大をする」アフィン変換の行列を取得するコードです。
if __name__ == "__main__":
src = np.array([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0]], np.float32)
dest = src.copy()
dest[:,0] *= 2
affine = cv2.getAffineTransform(src, dest)
print(affine)
# [[2. 0. 0.]
# [0. 1. 0.]]
この行列の値を式(2)方式に表記すれば、
\begin{cases}
x' = 2x \\
y' = y
\end{cases}\tag{4}
となり、x方向に2倍の拡大をしていることが明白です。
さて、いよいよ合成を考えます。もし$A_1$を「横方向に2倍の拡大」、$A_2$を「縦方向に2倍の拡大」と考えれば、
A_1=\begin{bmatrix}2&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix},
A_2=\begin{bmatrix}1&0&0 \\ 0&2&0 \\ 0&0&1 \end{bmatrix}\tag{5}
(1)式より、
A_2A_1=\begin{bmatrix}1&0&0 \\ 0&2&0 \\ 0&0&1 \end{bmatrix}\begin{bmatrix}2&0&0 \\ 0&1&0 \\ 0&0&1 \end{bmatrix}=\begin{bmatrix}2&0&0 \\ 0&2&0 \\ 0&0&1 \end{bmatrix}\tag{6}
これは「縦横方向に2倍の拡大」をしていることに他なりません。たまたまこの例では$A_1$と$A_2$の入れ替えができますが、**行列の積なので順番の入れ替えができない(可換ではない)**のに注意してください。可換ではないことは図形的にも明らかで、例えば横に100ピクセルシフトしてから縦横2倍拡大するのと、縦横2倍拡大してから横に100ピクセルシフトさせるのは出力結果が違うからです。
最初に「アフィン変換は三角形の点の写像だよ」と述べましたが、数学的には写像と関数はほぼ同じなので、$A_1, A_2$に対応する変換をプログラミングの関数で(抽象的な表記ですが)、
def a1(input):
return some_output #A_1の変換に対応
def a2(input):
return some_output #A_2の変換に対応
とすれば、$A_1, A_2$の合成は、
output = a2(a1(input))
となります。これは(1)の式そのものです。つまり、(プログラミングの)関数を行列で表すことができるから、はじめにそれらの行列の積を考えて、一本の合成関数の形で元の画像に作用させれば計算コストが軽くなるということができます。
アフィン変換10回で定義される操作があったとして、元の画像が4096×2160だったとしましょう。4096×2160の画像のアフィン変換を10回やるのはかなり重いですが、3×3行列の積は1000回やろうが大したことがないので、最初に3×3の行列10個分の積を取って、最後に1回だけ4096×2160の画像に対して合成した行列でアフィン変換をやれば軽くなります。これは大きなメリットです。
また多態性の点でもメリットがあります。結局はプログラムで書いている処理を行列計算に落とし込めるということなので、組み合わせ的に様々なバリエーションの処理を作ることが可能です。
さらにもう一個メリットがあります。それは境界箱などアノテーションデータの変換がやりやすいです。それは後ほど見ていきます。
回転(Rotate)
11.画像の左上を原点とした回転
理論的な解説
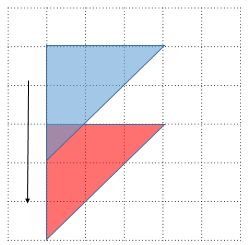
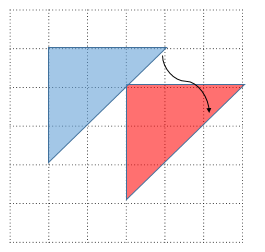
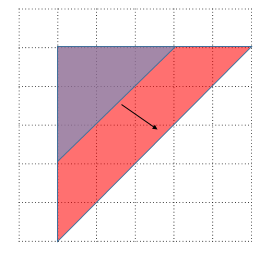
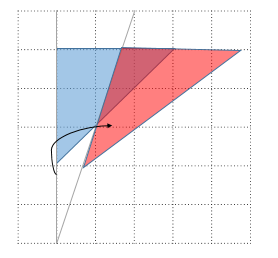
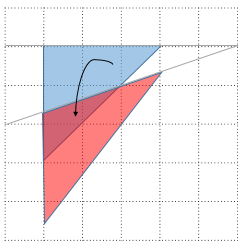
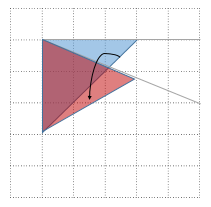
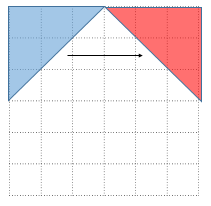
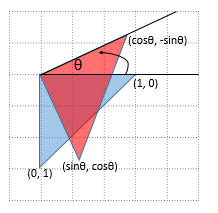
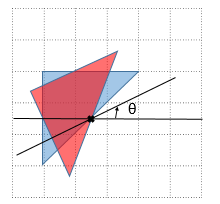
さていよいよ回転です。左上を原点として反時計回りにθだけ回転する操作を考えます。
このとき$(1,0)\to(\cos\theta, -\sin\theta), (0,1)\to(\sin\theta, \cos\theta)$に対応します。赤い三角形の右上の頂点から、x軸に向かって垂線を下ろして三角形の合同を考えるのがわかりやすいですね(符号に注意してください)。線形代数の回転行列の公式で、
\begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}\tag{7}
というのをご存知の方もいるかもしれませんが、数学のxy座標とはyの軸の向きが違うので(数学では上がyのプラス方向であるのに対して、OpenCVの座標系では下がyのプラス方向)、マイナスのつく位置が変わります。OpenCVが勝手に計算してくれるのでこの式は覚えなくていいです。
\begin{bmatrix}
\cos\theta & \sin\theta \\
-\sin\theta & \cos\theta
\end{bmatrix}\tag{8}
なのでこんな式が出てきても「ああ、座標系の違いなんだ」ぐらいに思っておけばOKです。右からxyの点の行列(単位行列)をかけて上の図と一致するのを確認してみてください。
OpenCVではgetRotationMatrix2Dという関数を使えば三角関数を明示的に使うことはありませんが、getAffineTransformによる三角形の写像による定義と一致することを確認しておきます。
60度($=\frac{\pi}{3}$ラジアン)回転する場合を考えます。
if __name__ == "__main__":
# 三角関数を使った書き方(π/3=60度回転させる場合)
src = np.array([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0]], np.float32)
dest = np.array([[0.0, 0.0], [np.sin(np.pi/3),np.cos(np.pi/3)], [np.cos(np.pi/3),-np.sin(np.pi/3)]], np.float32)
affine = cv2.getAffineTransform(src, dest)
print(affine)
#[[ 0.5 0.86602539 0. ]
# [-0.86602539 0.5 0. ]]
# getRotationMatrix2Dは度数法を使う(普段はこっちでOK)
rotate = cv2.getRotationMatrix2D((0.0,0.0), 60, 1.0)
print(rotate)
#[[ 0.5 0.8660254 0. ]
# [-0.8660254 0.5 0. ]]
このようにgetAffineTransformで求めた値と、getRotationMatrix2Dで求めた値が一致するのを確認できました。Numpyの三角関数はラジアンを代入するのに対して、getRotationMatrix2Dは1周を360度とする度数法で代入するのに注意しましょう。以下実装ではgetRotationMatrix2Dを使うので、三角関数を意識することはありません。
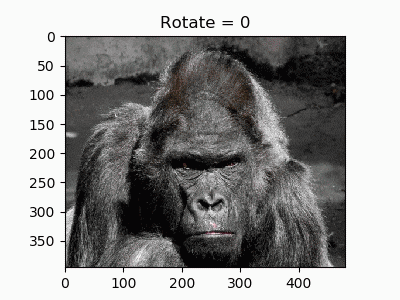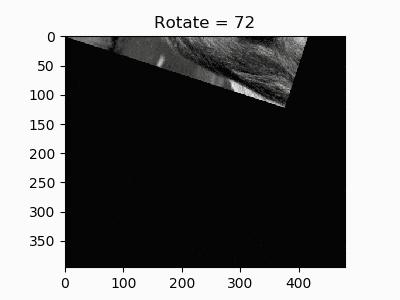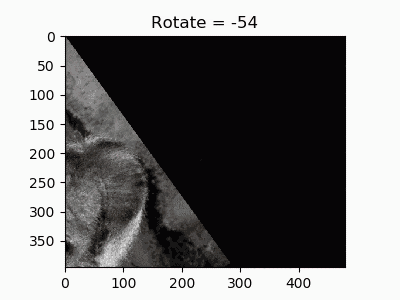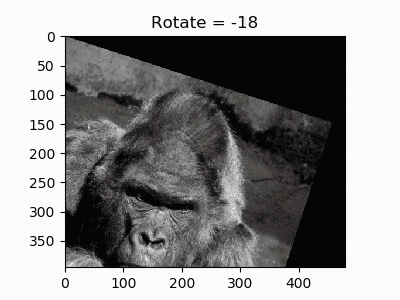
具体例
回転のコードはこれだけ。
def rotate(image, angle):
h, w = image.shape[:2]
affine = cv2.getRotationMatrix2D((0,0), angle, 1.0)
return cv2.warpAffine(image, affine, (w, h))
こうしてみると、回転というのはアフィン変換におけるほんの一部でしかないのがわかります。回転は「原点を固定して、三角形の辺の長さが維持されるという縛りをおいたアフィン変換」ということになりますね。
12.画像の中心を原点とした回転
左上を原点とすると画像が大きく切れてしまうので、中心を原点にして回転してみます。ほとんどコードは一緒です。
def rotate_center(image, angle):
h, w = image.shape[:2]
affine = cv2.getRotationMatrix2D((w/2.0, h/2.0), angle, 1.0)
return cv2.warpAffine(image, affine, (w, h))
内部的には回転と平行移動の合成変換をやっています。
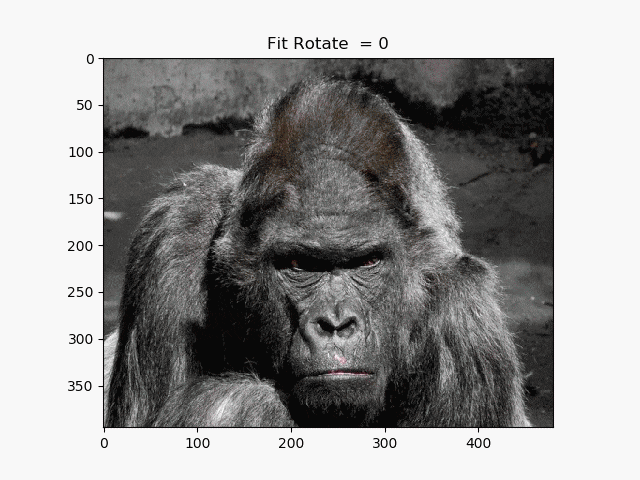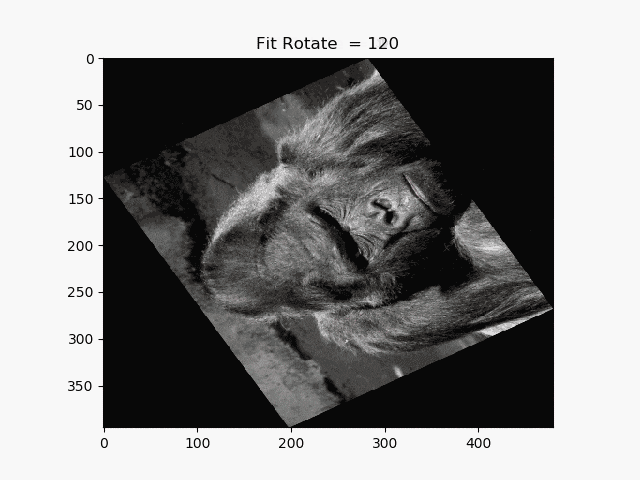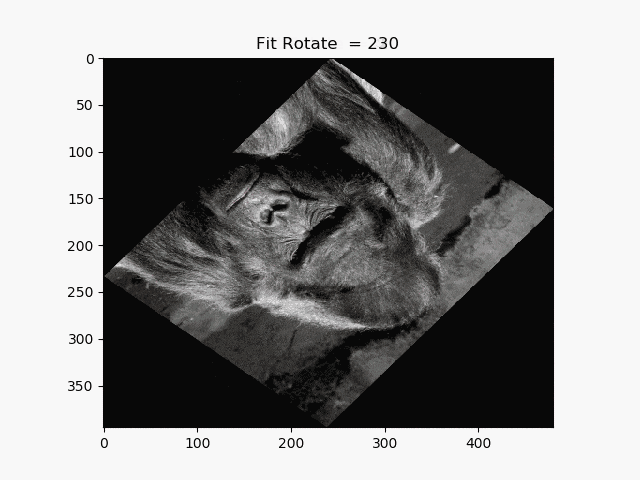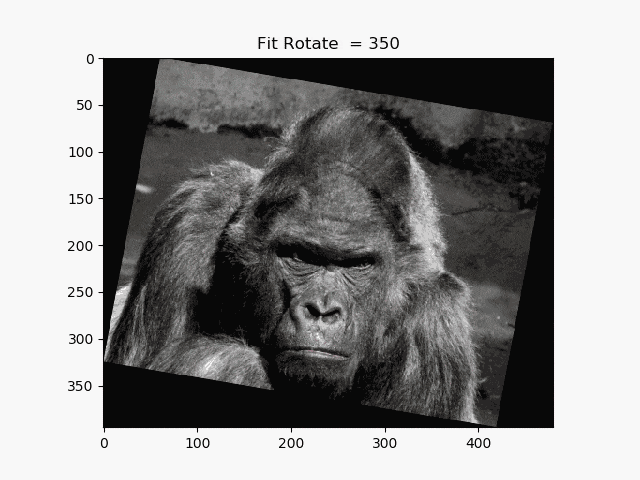
13.はみ出さない回転
しかし中心を原点にして回転しても微妙にはみ出してしまいます。完全にはみ出さない方法は、アフィン変換の合成を意識して使います。具体的には、
- 中心を原点にして回転させる
- 回転後の長方形のサイズ基準の中心を、元の画像の中心にあうように平行移動する
- 回転後の長方形のサイズを元のサイズと等しくなるようにリサイズ
いちいちコードでアフィンの合成を計算してもいいのですが、今回は決定的な振る舞いしかしないので合成アフィンを先に計算しておきます。理論的な導出はかなりややこしいので、気になる方は末尾の「おまけ(2)」を参照してください。やっていることは、こちらの記事の実装にリサイズを加えたものです。
def rotate_fit(image, angle):
h, w = image.shape[:2]
# 回転後のサイズ
radian = np.radians(angle)
sine = np.abs(np.sin(radian))
cosine = np.abs(np.cos(radian))
tri_mat = np.array([[cosine, sine],[sine, cosine]], np.float32)
old_size = np.array([w,h], np.float32)
new_size = np.ravel(np.dot(tri_mat, old_size.reshape(-1,1)))
# 回転アフィン
affine = cv2.getRotationMatrix2D((w/2.0, h/2.0), angle, 1.0)
# 平行移動
affine[:2,2] += (new_size-old_size)/2.0
# リサイズ
affine[:2,:] *= (old_size / new_size).reshape(-1,1)
return cv2.warpAffine(image, affine, (w, h))
アフィン変換しかやっていないことに注目してください。アフィン変換の合成が有用に機能することが確認できました。
アフィン変換と境界箱の変換(発展)
アフィン変換では反転(Flip)もできると書きましたが、普通に以下のようにNumpyで反転操作を書くと困ったことがおこります。
flip = image[:, ::-1, :]
それは画像になにかのアノテーションを加えるときに(物体検出に使われるような境界箱がわかりやすいでしょう)、アノテーションの変換をいちいち書かないといけないことです。
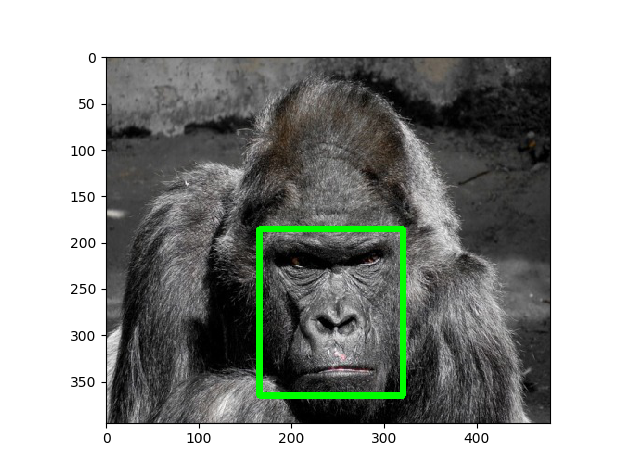
ゴリラの顔の領域をプロットしてみました。顔検出で用いられるアノテーションです。
def draw_face(image, bounding_box):
canvas= image.copy()
canvas = cv2.line(canvas, tuple(bounding_box[0,0]), tuple(bounding_box[0,1]), (0,255,0), 5)
canvas = cv2.line(canvas, tuple(bounding_box[0,0]), tuple(bounding_box[0,2]), (0,255,0), 5)
canvas = cv2.line(canvas, tuple(bounding_box[0,1]), tuple(bounding_box[0,3]), (0,255,0), 5)
canvas = cv2.line(canvas, tuple(bounding_box[0,2]), tuple(bounding_box[0,3]), (0,255,0), 5)
return canvas
if __name__ == "__main__":
image = cv2.imread("gorilla.jpg")[:,:,::-1]
bbox = np.array([[[165,185],[320,185],[165,365],[320,365]]], np.float32)
image = draw_face(image, bbox)
plt.imshow(image)
plt.show()
さて問題です。この画像を回転や反転するときに、顔の領域のアノテーション(境界箱)をどうやってセットで変換しますか? いちいちif文で書きますか?
アフィン変換の式を思い出しましょう。
\begin{cases}
x' = ax+by+x_0 \\
y' = cx+dy+y_0
\end{cases} \tag{2}
このように行列計算で座標が変換されました。またアフィン変換同士は合成することができます。つまり、アノテーションもアフィン変換で座標変換してあげればよいのです。先程の「はみ出さない回転」でも結局はアフィン変換の合成なので、このように顔領域を描画しながら回転することができます。
def rotate_fit_with_bb(image, angle):
h, w = image.shape[:2]
# 画像の変換
# 回転後のサイズ
radian = np.radians(angle)
sine = np.abs(np.sin(radian))
cosine = np.abs(np.cos(radian))
tri_mat = np.array([[cosine, sine],[sine, cosine]], np.float32)
old_size = np.array([w,h], np.float32)
new_size = np.ravel(np.dot(tri_mat, old_size.reshape(-1,1)))
# 回転アフィン
affine = cv2.getRotationMatrix2D((w/2.0, h/2.0), angle, 1.0)
# 平行移動
affine[:2,2] += (new_size-old_size)/2.0
# リサイズ
affine[:2,:] *= (old_size / new_size).reshape(-1,1)
converted_image = cv2.warpAffine(image, affine, (w, h))
# アノテーションの変換
# 元の画像の顔の領域(Bounding Boxが複数ある場合にそなえて3階で定義)
bbox = np.array([[[165,185],[320,185],[165,365],[320,365]]], np.float32)
bbox_matrix = np.concatenate([bbox, np.ones((bbox.shape[0],bbox.shape[1],1), np.float32)], axis=-1)
# 変換後の顔の領域
converted_bbox = np.tensordot(affine, bbox_matrix.T, 1).T
return draw_face(converted_image, converted_bbox.astype(np.int32))
def draw_face(image, bounding_box):
canvas= image.copy()
canvas = cv2.line(canvas, tuple(bounding_box[0,0]), tuple(bounding_box[0,1]), (0,255,0), 3)
canvas = cv2.line(canvas, tuple(bounding_box[0,0]), tuple(bounding_box[0,2]), (0,255,0), 3)
canvas = cv2.line(canvas, tuple(bounding_box[0,1]), tuple(bounding_box[0,3]), (0,255,0), 3)
canvas = cv2.line(canvas, tuple(bounding_box[0,2]), tuple(bounding_box[0,3]), (0,255,0), 3)
return canvas
テンソル計算が出てきてややこしいですが、境界箱が1つでよければ行列計算にすることができます。
このように完璧ですね。Bounding Boxが複数の場合でもいけます。
冒頭に出したアニメーションはこのように求めました。
真価はランダムな処理(発展)
まだまだアフィン変換を使ってみましょう。アフィン変換の真価はランダムな処理です。以下のようなケースでも、境界箱を書くことができます。
- 50%の確率で左右反転
- 左右-20~20ピクセル、上下-15~15ピクセルのランダムクロップ
- 0度~90度の回転をし、画像が切れないようにする
- 1~3と同じ処理を5個のBounding Boxに施して移動させる
正直こんなのif文とかで書きたくありません。でもアフィン変換なら全部を1つの変換に結合できるのでできます。ちょっと大変ですがこれまでの複合です。
import cv2
import matplotlib.pyplot as plt
import numpy as np
def get_affine_matrix(affine):
mat = np.eye(3)
mat[:2,:] = affine
return mat
def complicated_transform(image, bounding_box):
h, w = image.shape[:2]
# Horizontal flip
src = np.array([[0.0, 0.0],[0.0, 1.0],[1.0, 0.0]], np.float32)
dest = src.copy()
dest[:,0] = w - src[:,0]
if np.random.rand() >= 0.5:
A1 = get_affine_matrix(cv2.getAffineTransform(src, dest))
else:
A1 = np.eye(3) # 何もしないのは単位行列(恒等変換)
# Random crop
shift_points = np.array([40.0, 30.0], np.float32)
dest = src + (shift_points * np.random.rand(1,2)).astype(np.float32) - shift_points / 2.0
A2 = get_affine_matrix(cv2.getAffineTransform(src, dest))
# 回転後のサイズ
radian = np.random.uniform(0.0, np.pi/2.0)
sine = np.abs(np.sin(radian))
cosine = np.abs(np.cos(radian))
tri_mat = np.array([[cosine, sine],[sine, cosine]], np.float32)
old_size = np.array([w,h], np.float32)
new_size = np.ravel(np.dot(tri_mat, old_size.reshape(-1,1)))
# 回転アフィン
rotate_affine = cv2.getRotationMatrix2D((w/2.0, h/2.0), np.degrees(radian), 1.0)
rotate_affine[:2,2] += (new_size-old_size)/2.0
rotate_affine[:2,:] *= (old_size / new_size).reshape(-1,1)
A3 = get_affine_matrix(rotate_affine)
# アフィンの合成
affine = np.dot(A3, np.dot(A2, A1))
converted_image = cv2.warpAffine(image, affine[:2,:], (w, h))
# アノテーション
bbox_matrix = np.concatenate([bounding_box,
np.ones((bounding_box.shape[0],bounding_box.shape[1],1), np.float32)], axis=-1)
converted_bbox = np.tensordot(affine[:2,:], bbox_matrix.T, 1).T
return draw_face(converted_image, converted_bbox.astype(np.int32))
def draw_face(image, bounding_box):
canvas= image.copy()
for i in range(bounding_box.shape[0]):
canvas = cv2.line(canvas, tuple(bounding_box[i,0]), tuple(bounding_box[i,1]), (255,0,0), 2)
canvas = cv2.line(canvas, tuple(bounding_box[i,0]), tuple(bounding_box[i,2]), (255,0,0), 2)
canvas = cv2.line(canvas, tuple(bounding_box[i,1]), tuple(bounding_box[i,3]), (255,0,0), 2)
canvas = cv2.line(canvas, tuple(bounding_box[i,2]), tuple(bounding_box[i,3]), (255,0,0), 2)
return canvas
if __name__ == "__main__":
image = cv2.imread("cats.jpg")[:,:,::-1]
bbox = np.array([[[15,105],[60,105],[15,148],[60,148]],
[[157,41],[208,41],[157,78],[208,78]],
[[240,87],[292,87],[240,133],[292,133]],
[[308,129],[381,129],[308,180],[381,180]],
[[430,74],[459,74],[430,115],[459,115]]], np.float32)
bbox_matrix = np.concatenate([bbox, np.ones((bbox.shape[0],bbox.shape[1],1), np.float32)], axis=-1)
for i in range(20):
img = complicated_transform(image, bbox)
plt.clf()
plt.imshow(img)
plt.savefig(f"tmp/complicated_{i:02}.png")
個々の処理の結合はただの行列積です。つまり、関数の結合が行列計算でできるということです。これを知ってしまうと線形代数急に好きになりますよね。
猫の順番が左右入れ替わっていることがある(最初の左右反転が効いている)のに注目してみてください!
まとめ
とても長くなってしまいましたが、アフィン変換はとても強力な手法です。ポイントだけかいつまむと、
- アフィン変換は三角形の変形を定義することで決まる変換
- アフィン変換は行列の積を取ることで合成して1つの変換と考えることができる
- 合成して1つの変換にしたほうが、計算量やアノテーションの変換という点では都合がいい。Numpyでかけるような処理でも、多態性をもたせるケースでは、1つのアフィン変換に書いたほうが見通しが効きやすいことがある。
ということでした。回転だけでなくぜひ使いこなしてみてください。
(おまけ1)証明
「三角形の移動が与えられれば変換が決まる」ということについて証明します。
平面のアフィン変換を
\begin{cases}
x' = ax+by+x_0 \\
y' = cx+dy+y_0
\end{cases} \tag{2}
にしたがって、点$(x,y)$を点$(x',y')$に移す変換であると定義すれば、それぞれ$x',y'$についての連立方程式とみなせる。それぞれ3元の連立方程式なので、$(a,b,x_0),(c,d,y_0)$を求めるには、3点分の座標が必要。三角形が与えられたときに、互いの辺のベクトルは一次独立なので、連立方程式の解は1つになる。したがって、変換を一意に決めることができる。
(おまけ2)「はみ出さない回転」のアフィン変換の合成の計算
回転→平行移動→リサイズの順で適用する。それぞれのアフィン変換の行列を$A_1, A_2, A_3$とすると、アフィン変換の合成の公式により、
$$A = A_3A_2A_1 $$
となる。成分を使って書くと、
A_1=\begin{bmatrix}
a_1 & a_2 & a_3 \\
a_4 & a_5 & a_6 \\
0 & 0 & 1
\end{bmatrix}
A_2=\begin{bmatrix}
1 & 0 & T_x \\
0 & 1 & T_y \\
0 & 0 & 1
\end{bmatrix}
A_3=\begin{bmatrix}
S_x & 0 & 0 \\
0 & S_y & 0 \\
0 & 0 & 1
\end{bmatrix}
となる。回転のアフィンは出てくる値が様々なので$a_1,\dots,a_6$の値を使って示している。その他の式はこちらのサイトを参照。積を計算すると、
\begin{align}
A_3A_2A_1&=\begin{bmatrix}
S_x & 0 & 0 \\
0 & S_y & 0 \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
1 & 0 & T_x \\
0 & 1 & T_y \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
a_1 & a_2 & a_3 \\
a_4 & a_5 & a_6 \\
0 & 0 & 1
\end{bmatrix} \\
&= \begin{bmatrix}
S_x & 0 & S_xT_x \\
0 & S_y & S_yT_y \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
a_1 & a_2 & a_3 \\
a_4 & a_5 & a_6 \\
0 & 0 & 1
\end{bmatrix} \\
&= \begin{bmatrix}
S_xa_1 & S_xa_2 & S_xa_3+S_xT_x \\
S_ya_4 & S_ya_5 & S_ya_6+S_yT_y \\
0 & 0 & 1
\end{bmatrix}
\end{align}
なのでこの行列の2行目までを取ると、「13.はみ出さない回転」のコードに示した通りになる。
また、回転後の長方形のサイズは、元のサイズを$(w,h)$、回転後を$(w',h')$とすると、
\begin{bmatrix}
w' \\ h'
\end{bmatrix} =
\biggl|\begin{bmatrix}
\sin\theta & \cos\theta \\
\cos\theta & \sin\theta
\end{bmatrix} \biggr|
\begin{bmatrix}
w \\ h
\end{bmatrix}
で求められる。これは回転した長方形を書いてみると求められる。