Go to Qiita Advent Calendar 2024 Top
LoginSignup
3446
3580

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@icoxfog417

画像処理の数式を見て石になった時のための、金の針

Last updated at Posted at 2016-01-31

画像処理は難しい。
Instagramのキレイなフィルタ、GoogleのPhoto Sphere、そうしたサービスを見て画像は面白そうだ！と心躍らせて開いた画像処理の本。そこに山と羅列される数式を前に石化せざるを得なかった俺たちが、耳にささやかれる「難しいことはOpenCVがやってくれるわ。そうでしょ？」という声に身をゆだねる以外に何ができただろう。

本稿は石化せざるを得なかったあの頃を克服し、OpenCVを使いながらも基礎的な理論を理解したいと願う方へ、その道筋(アイテム的には金の針)を示すものになればと思います。
扱う範囲としては、あらゆる処理の基礎となる「画像の特徴点検出」を対象とします(実践 コンピュータビジョンの2章に相当)。なお、本記事自体、初心者である私が理解しながら書いているため、上級画像処理冒険者の方は誤りなどあれば指摘していただければ幸いです。

画像の特徴点とは

人間がジグソーパズルを組み立てられるのはなぜか？と考えると、私たちはパズルの各ピースの特徴を把握して、それと似た、また連続する特徴を見つけ出して繋ぎあわせているのだ、と考えることができます。同様に、複数の写真をつなげてパノラマ写真にすることができるのは、写真間で共通する特徴を見つけ出して繋ぎあわせているからです。

image
CS231M Mobile Computer Vision Class,Lecture5, Stitching + Blending, p4~

この「特徴点」をどんどんシンプルに考えていくと、最終的には以下3つに集約できます。

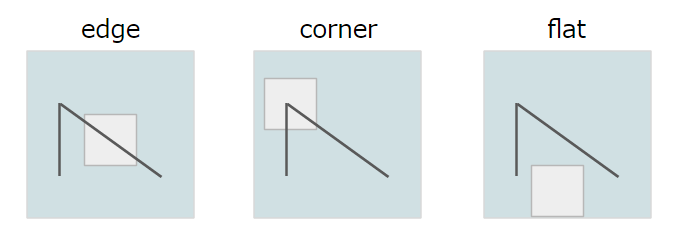
image

  • edge: 差異が認識できる境界がある
  • corner: edgeが集中する点
  • flat: edgeでもcornerでもない、特徴が何も認識できない点

そして、上記のようなパノラマ写真の合成などを行うことを考えると、この「特徴点」を見つける際には以下のルールにのっとる必要があります。

  • 再現性: ある特徴点は常に特徴点として認識される
  • 識別性: ある特徴点は、その他の特徴点と明確に異なると識別できる

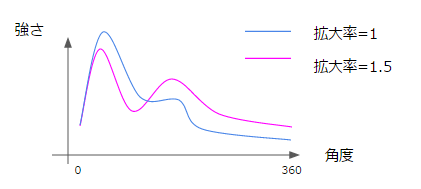
再現性については、例えば写真をとる角度を変えた場合に認識される特徴点がガラッと変わる、となると特徴点同士をつなぎ合わせるという処理そのものが破たんしてしまいます。

image

そのため、画像の角度や拡大率などで変化しない、頑健な特徴点を認識できる方がいいことになります。

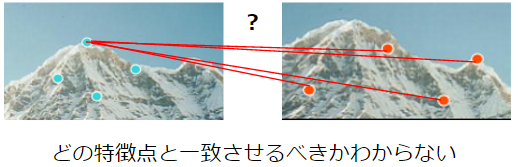
識別性については、認識した特徴点が一意に識別できないとどれとどれを一致させていいかわからなくなってしまいます。

image

そのため、各特徴点が一意に識別できる表現方法が重要になります。

これはそのまま、特徴点の検出(Feature Detection)、特徴点の表現方法(Feature Description) 、それぞれに求められることと一致します。つまり、「画像の角度や拡大率などで変化しない、頑健な特徴点」を検出し(Feature Detection)、それをなるべく「一意に識別できる表現方法」で表現すること(Feature Description)が、画像における特徴点の認識の目標になります。

では、特徴点の検出、特徴点の表現方法を順番に見ていきます。

特徴点の検出(Feature Detection)

特徴点を検出する手順としては、概ね「edgeを検出」し、次いでedgeが集中する「cornerを検出」する、という流れになります。

edgeの検出

edgeとは、具体的には「輝度が大きく変化している点」になります。
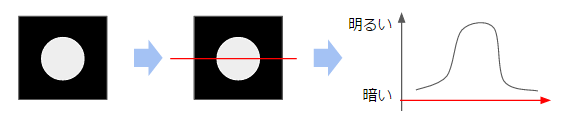
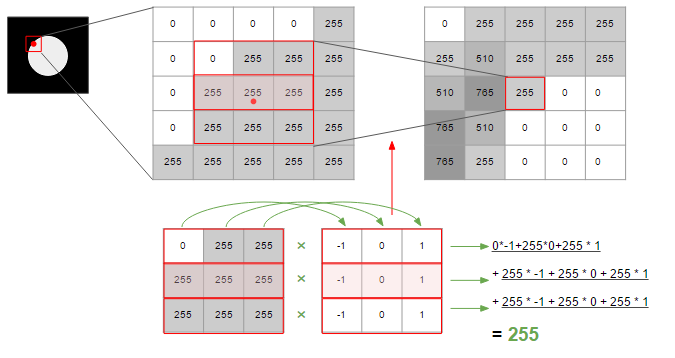
簡単な例として、真っ黒なタイルに白い円が描かれた画像を考えます。下図の通り真横から引いた赤い線上の輝度を座標軸に沿ってプロットすると、真ん中の白い円の中で輝度が跳ね上がっているようなグラフが得られるはずです。

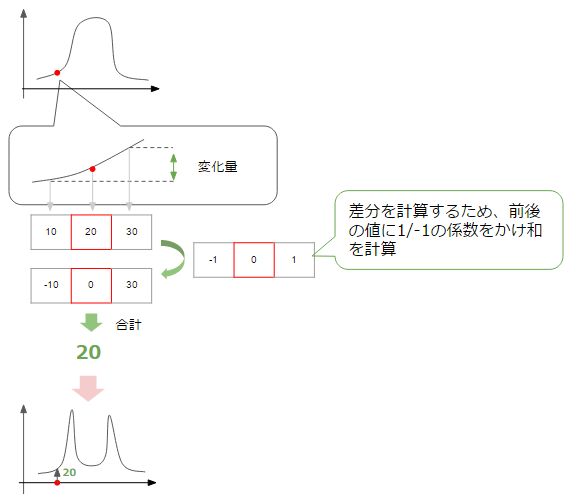
image

ここで、私たちが検出したいのはedge、つまりグラフ上で暗い->明るい、明るい->暗いと大きく変化しているポイントになります。ある点における変化の度合いを知るために、その点を中心とした前後の点の値の値から変化率を計算してみます。

image

すると、上図のように変化が大きな点、つまりedgeに該当する箇所で変化率が上がっているグラフが得られます(変化量には+-がありますが、ここでは絶対値をプロットしていると思ってください)。今は図の水平方向で変化量を考えていますが、垂直方向の場合にも同様に考えられます。

最終的には、水平方向、垂直方向双方の変化量を合計し(通常は二乗和平方根)、その値があるしきい値(threshold)より大きい点を収集すればedgeの検出ができそうです。

これがedge検出の基本的な考え方で、一応これだけでもedgeの検出は可能ですが、より精度の高い検出を行うためのいくつかのテクニックがあるのでそれを見ていきます。

スムージング

変化量を計算する際に、周辺部分も考慮する方法です。ざっくり言ってしまえば、平均をとるようなイメージです。平均をとれば値の変化をならすことができ(スムージング)、この結果滑らかにつながるedgeを検出することができます。

以下は、水平方向の変化量について、隣接する点の変化量も加味して計算する様子を図で表したものです。計3つの変化量の和をとることで、スムージングが実現されています。

image

上図では変化量を計算するために3*3の、-1/0/1の値が入った行列を使って計算しています。こうした変化量を計算するための行列や処理をフィルタと呼びます。

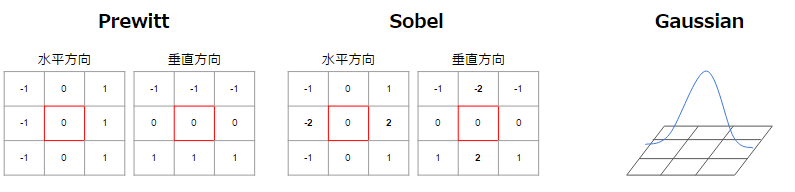
このフィルタには様々な種類があり、上図で使っていたのはこのうちのPrewittフィルタになります。SobelフィルタはPrewittより中心に隣接するものを重視したものになり、Gaussianは正規分布の関数を利用し、中心を頂点とし、端に向かってなだらかに係数をかけることができます。edgeの検出でよく利用されるCanny法は、このGaussianフィルタを使った方法になります。

image

なお、画像の端の部分については、隣接する点がないため補間を行う必要があります。この補間の方法には以下のような手法があります。

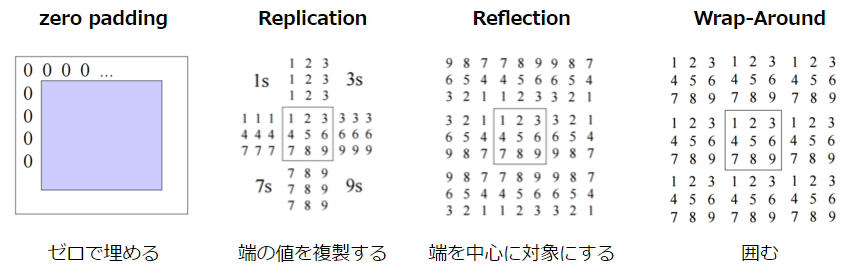
image
CSE/EE486 Computer Vision I, Lecture3, p26~

edgeの検出については、以上になります。ここまでの内容をまとめておきます。

  • edgeを検出するには、画像における輝度の変化量を手掛かりにする
  • 変化量は水平方向と垂直方向の2方向でとることができる。この値の二乗和平方根を変化量とし、これをMagnitudeと呼ぶ
  • Magnitudeが一定のしきい値を超えた場合にedgeと判定することで、edgeの検出が可能になる
  • 変化量を計算する際には、一般的にはスムージングを行う。これは周辺の変化量を加味することで、検出精度を上げるためのものである
  • この「周辺」の対象範囲と、それに対する重みづけを定義するのがフィルタであり、様々な種類がある

cornerの検出

続いては、cornerの検出です。ここでは、cornerの検出によく利用されるHarris Corner Detectorについて説明していきます。これは行列の特性を非常にうまく利用した手法で、直観的には主成分分析に近いイメージになります。

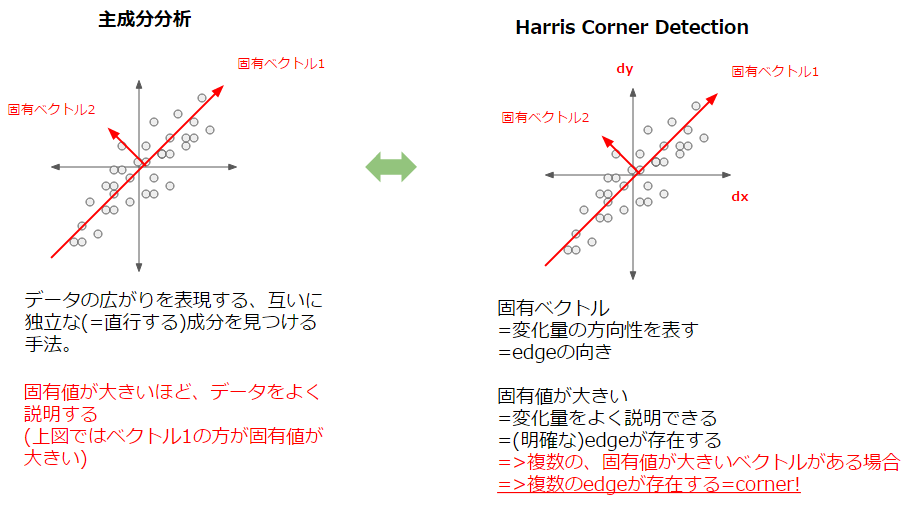
image

主成分分析の細かい説明は他の記事に譲りますが、重要なポイントは以下2点です。

  • データの広がる方向をよく説明できる指標を見つける。これは行列の固有ベクトルに相当する。
  • 計算の結果得られる固有値は、その指標の説明能力を表す

これをHarrisに当てはめると、「データ」は当然ある点における水平方向・垂直方向それぞれの変化量をまとめたものになります。そうすると、上記の主成分分析の説明から以下のように類推できます。

  • 固有ベクトルは「変化量の広がる方向」、つまりedgeの向きを表している
  • 固有値が大きい場合は、「変化量の説明能力が高い」、つまりedgeの強さを表している

これによりまずedgeの検出が可能になり、そして「固有値が大きい複数の固有ベクトル」が存在する場合、それは即ち複数のedgeがある、つまりcornerであるということになります。
固有値をそれぞれ$\lambda1$、$\lambda2$とすると、その値の大きさにより以下のように分類が可能です。

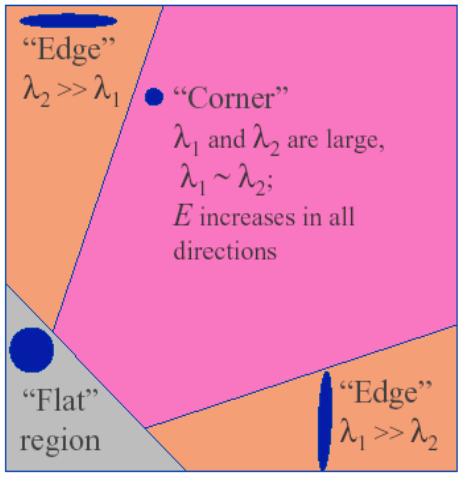
image
CSE/EE486 Computer Vision I, Lecture 06, Corner Detection, p19

数式の説明もしておきます。まず、画像$I$上のある点$I(x, y)$と、$x$方向に$u$、$y$方向に$v$移動した点$I(x+u, y+v)$との間の変化量を$E(u, v)$とすると、式で以下のように表せます。

$$
E(u, v) = \sum_{x, y} w(x, y) [I(x+u, y+v) - I(x, y)]^2
$$

$w(x, y)$はウィンドウ関数で、フィルタになります(Gaussian)。変化量が$[I(x+u, y+v) - I(x, y)]^2$で、これを$w(x, y)$でスムージングして変化量を算出する、というイメージです。
この式をテイラー展開を使って近似すると以下のようになります(展開式は省略。興味ある方は、上図のリンクの講義資料をご参照ください)。

E(u, v) \simeq [u, v] M \begin{bmatrix} u \\ v \end{bmatrix}

ここで、$M$は以下になります。

M = \sum_{x, y} w(x, y) \begin{bmatrix} I_X^2 & I_x I_y \\ I_x I_y & I_y ^2 \end{bmatrix}

$I_x$、$I_y$はそれぞれx軸、y軸での差異で$[I_x, I_y]$を二乗すると上記の行列部分になります。やっていることは上記の式の$[I(x+u, y+v) - I(x, y)]^2$と変わりません。そして、これこそが「変化量を記述した行列」で、これを特異値分解することで冒頭で述べたようなedge、cornerの判定が可能になります。

ただ、固有値の計算は結構手間なので、必要ないところではなるべく計算しないようにします。そのために利用されるのが、以下の指標です。

R = det M -k(trace M)^2

det M = \lambda1 \lambda2

trace M = \lambda1 + \lambda2

$k$は定数で、だいたい0.04~0.06くらいです。Rの値によって以下のように分類できます。

  • Rが大きい: corner
  • Rが小さい: flat
  • R < 0: edge

図にすると、以下のようになります。

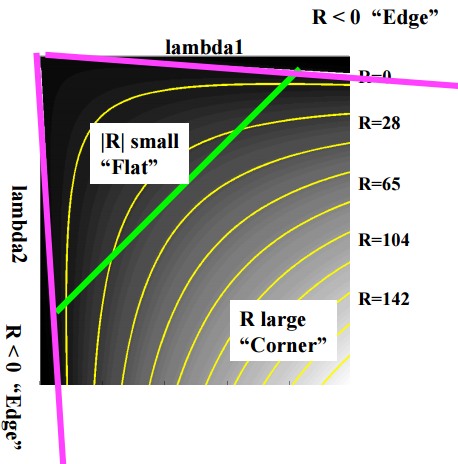
image
CSE/EE486 Computer Vision I, Lecture 06, Corner Detection, p22

これで手早くcornerを検出できるようになりました。ここで、corner検出についてまとめておきます。

  • cornerは複数のedgeが集まる箇所と定義できる
  • 変化量をまとめた行列の固有ベクトルからedgeの向き、固有値の大きさから変化量の大きさ(edgeらしさ)がわかる
  • 2つの固有値の値を基に、edge、corner、flatを判定できる
  • 固有値の計算は手間であるため、判定式を利用し計算を簡略化する

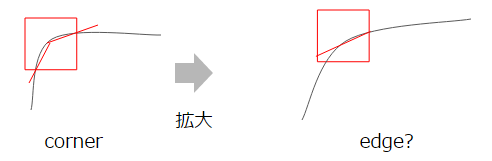
なお、Harrisはedgeの向きである固有ベクトルを考慮するため、画像の傾きなどに対し頑健です。ただ、スケール(拡大)については頑健ではありません。これは、拡大するにつれcornerが緩やかになり、edgeが区別しにくくなるためです。

image

これを克服するための編み出された手法がFASTになります。詳細は割愛しますが、中心点を基準としてそれより暗いor明るいn点の連なりを認識する方法です。これは文字通りFASTな手法でかつ回転・拡大に対し共に頑健です。

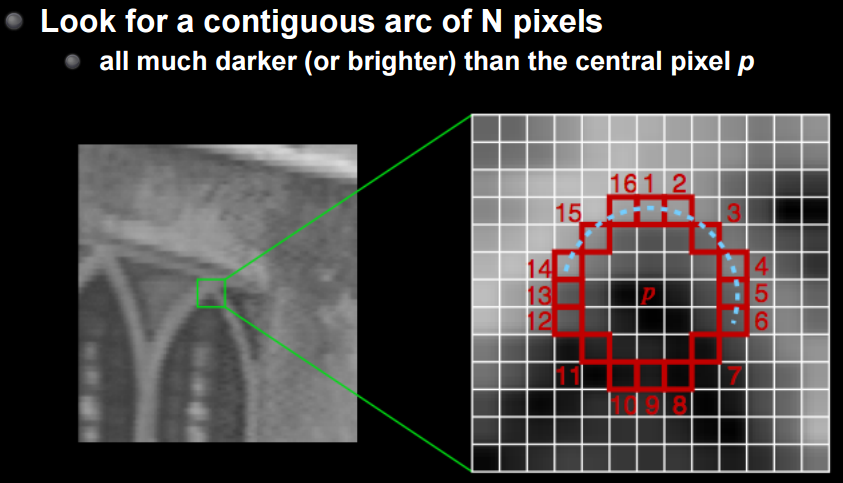
image
CS231M Mobile Computer Vision Class,Lecture5, Stitching + Blending, p24

特徴点の表現方法(Feature Description)

これで特徴点は検出できるようになりました。今度は、その特徴点を利用してなるべく一意な特徴表現、Feature Descriptionを作成することで画像のマッチングなどが行えるようにしたいです。

今までも少し触れましたが、このFeature Descriptionにとって望ましい特性は以下3点です。

  • Translation: 画像のスライドに対して頑健
  • Rotation: 画像の回転に対して頑健
  • Scaling: 画像の拡大/縮小に対して頑健

Translationは単に位置が変わるだけなので対応は割と簡単で、前項のHarrisでも上げた通りRotationも何とかなります。ただ、Scalingへの対応、これは難しいです。下図から明らかなとおり、画像内の情報は拡大率によって著しく変わってしまうためです。

image
CSE/EE486 Computer Vision I, Lecture 31, Object Recognition : SIFT Keys, p31

そもそも、拡大をしたのならマッチングさせる範囲もそれに合わせて拡大しなければ、情報が落ちてしまうのは自明です。なぜなら同じ範囲でも収まる領域が変わってくるためです。

image

つまり、上述の3点の特性を満たすにはスケールを考慮する必要があります。Harrisでは固有ベクトルと固有値から「向き」と「強さ」だけでしたが、ここに「スケール」、つまりどの拡大値で得られるものなのか、を加味するということです。イメージ的には以下のような感じになります。

image

そして、このスケールを加味した特徴点の検出・記述を可能にするのがSIFTという手法になります。

SIFT (Scale Invariant Feature Transform)

SIFTの肝になっているのが、スケールごとの特徴点抽出になっています。これに使われているのがLoG/DoGという手法です。LogはLaplacian of Gaussianの略で、Gaussianフィルタでスムージングした画像の中の、変化量が最大の点を2回微分(=Laplacian)で求めるというものです。
Gaussianについてはスムージングで述べた通りなので、2次微分(=Laplacian)でなぜ変化量が最大の点が求められるのかについて簡単に説明します。

image

微分とは、端的にはある点における変化量を求めるものだと思ってください。そうすると、以下のようなことがわかります。

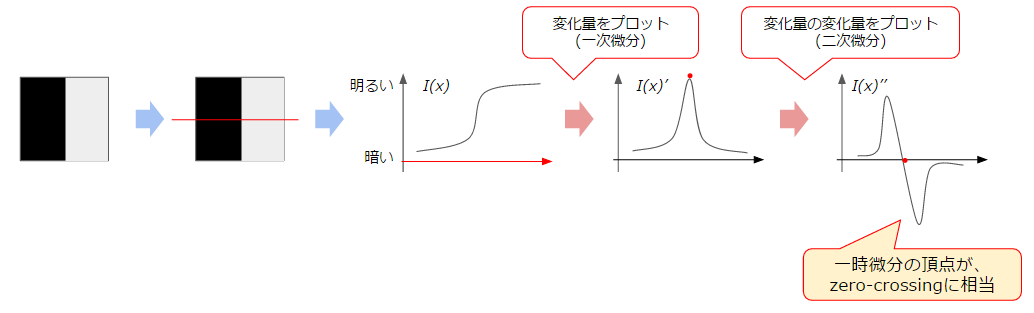
  • 1次微分: 元の関数に対する変化量を表す=頂点が、変化量が最大(最小)の点を表す
  • 2次微分: 変化量の変化を表す=1次微分の頂点付近では、変化の方向の切り替わりが発生する=1次微分の頂点は、軸と交わる点(zero-crossing point)と等しくなる

つまり、$I(x)''=0$となる点が変化量が最大の点、特徴点として上げられるということです。この2次微分をかけるのに相当するフィルタを「ラプラシアン・フィルタ」と呼び、値が0に近いほど特徴点の可能性が高くなります。
※ただ、2次微分だけでは、1次微分の段階で0(=変化なし)な点と頂点のものとが区別できないので、1次微分の値が十分に大きいかを同時に見る必要あります。このことからもわかる通り、ノイズにとても弱いです。

そして、LoGに戻るとこれはその名の通り、Gaussianフィルタでスムージングをしてから、ラプラシアンフィルタで変化量が最大の点=特徴点を求めるという手法になります。
そして、LoGではGaussianフィルタを使うため、その$\sigma$(分散)を調整することができます。$\sigma$は大きいほどスムージングが強力にかかるため、変化量が大きい点が集まっているところしか検出できなくなります。これは逆もしかりで、感の良い方は気づいたかもしれませんが、これはちょうど拡大率を操作してみているのと同じ役割を果たしています。

image

スクリーンショット 2016-02-04 13.37.57.png

CSE/EE486 Computer Vision I, Lecture 11, LoG Edge and Blob Finding, p19

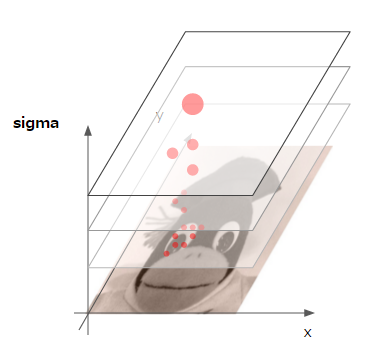
SIFTでは、この$\sigma$を調整した複数の階層を用意して特徴点の検出を行います(スケールスペース)。以下は、その図になります。

スクリーンショット 2016-02-04 13.45.53.png

ここでは、LoGの計算を簡略化するために、$\sigma$を変えた2つの層の差分で近似を行っています。これがDoG(Difference of Gaussian)になります。発見された特徴点は、スケールに対し頑健かを見るため前後のスケールと比較します(周辺8点と、前後のスケールにおける各9点、計26点と比較)。

これで、スケールに頑健な特徴点がわかるようになりました。後はこの特徴点における変化量の「強さ」と「向き」ですが、これは変化量とその角度から取得します。

スクリーンショット 2016-02-04 13.30.42.png

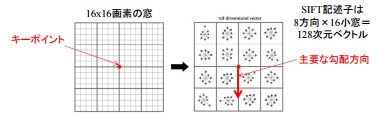
ここで、SIFTでは単一の特徴点だけでなく、それを中心とした16*16のマスを考慮します(この「マス」の大きさをbin sizeと呼びます)。

image
意味的マルチメディア処理 第A2回, p4

それをさらに4x4の領域に区切っていき、そこで縦軸に変化量(変化量のMagnitude)、横軸に向き(=変化量の勾配の角度)を取ったヒストグラムを作成します。

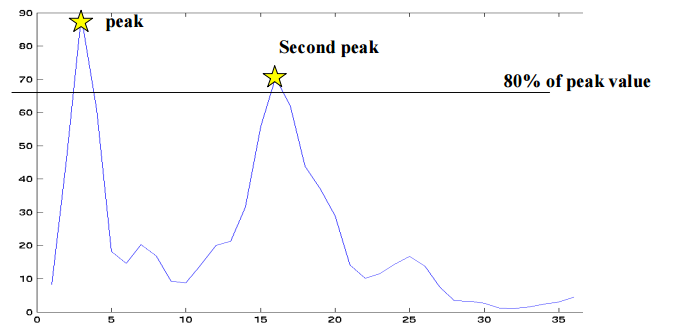
image
CSE/EE486 Computer Vision I, Lecture 31, Object Recognition : SIFT Keys, p24

上図は0〜36(360度に対応)でまとめていますが、最終的には8方向にまとめます。そうすると、4*4の各窓が8方向の要素を持つベクトルが出来上がります。この全128次元のベクトルがSIFT Vectorであり、これは「スケール」に対し頑健であり、「強さ」と「向き」がわかるという、3つの特性を備える特徴点記述になります。

このSIFT Vectorを利用することで、非常に精度の高い特徴点のマッチングなどが行えるようになります。

特徴点検出方法の進化

上記で挙げた特徴点の検出や記述の手法は年々進化しています。以下はSIFT登場前後までの手法の進化です。回転・スケールに対し頑健な特徴量を得ていく過程がわかるかと思います。

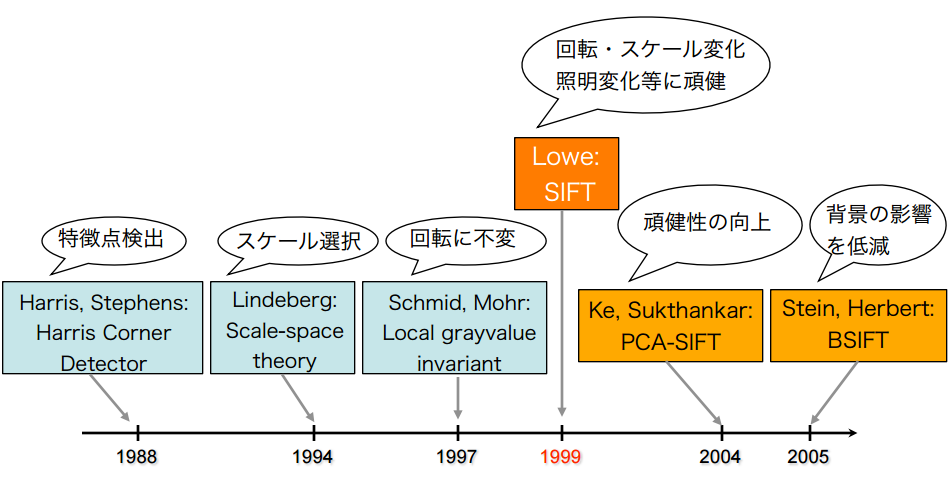
image
MIRU2013チュートリアル：SIFTとそれ以降のアプローチ, p5

こちらはSIFT以降の進化になります。SIFTを高速化されたSURFという手法もよく使われます。なお、SIFTもSURFも特許が取られています。SIFTは2020/3/6に特許が切れ、OpenCVでもNON FREEから外れましたが、SURFの利用にあたってはまだ特許料が発生します。そのため、ここまで説明しておいてなんですが、実際利用するにあたってはORBや、OpenCV 3.0で追加されたAKAZEなどが良いようです。何もSIFT/SURFより高速です。

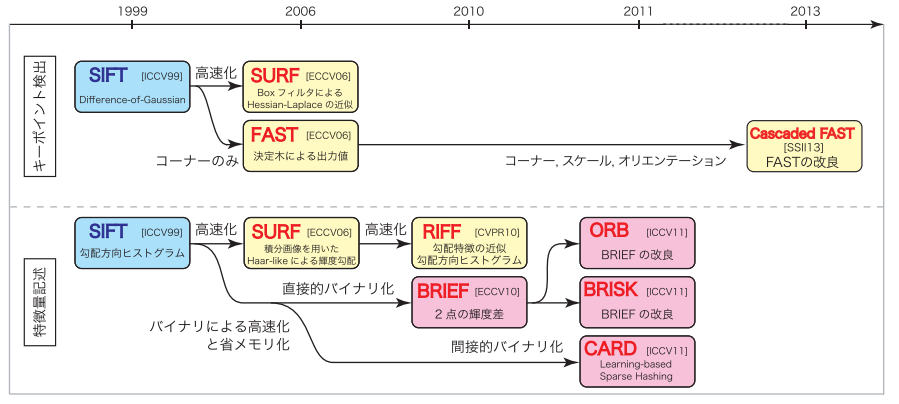
image
MIRU2013チュートリアル：SIFTとそれ以降のアプローチ, p93

今回ご紹介した基礎的な手法を理解しておけば、今後新しい手法が登場したときも、何が改良されてきたのかがわかり易くなると思います。

特徴点のマッチング

検出した特徴点は、様々な用途に使えます。代表的な例として、画像のマッチングに使用する方法を紹介したいと思います。

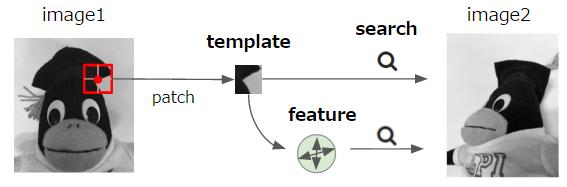
まず、画像のマッチングに際しては比較対象とする特徴点の周辺領域を切り出し(この切り出したものをパッチといいます)、それがもう片方の画像にもあるか調べる、というのが基本的な流れになります。このパッチをどう使うかについて、以下の2種類があります。

  • Templateベース: もう片方の画像にパッチと一致するものがないか確認する
  • Featureベース: パッチから特徴を抽出し、その特徴と一致するものがないか確認する

イメージ的には下図のようになります。

image

いずれにせよ、比較を行う際には類似度(similarity)を測るための関数が必要になります。※画像の全範囲について類似度を計算していると大変なので、探索範囲を絞る方法も必要になってきますが、ここでは触れません。

類似度を測る代表的な指標としては、以下があります。

  • SSD (sum of squared differences): 差の二乗和
  • NCC (normalized cross correlation): 正規化した相互相関

SSDは一番単純な指標で、TemplateやFeature同士の差を見て0に近ければ類似しているとする方法です。どれくらいの距離であればよいか、つまり閾値については、最も一致する特徴点との比率が用いられることが多いです。
NCC、というか相互相関は類似性を示す尺度で、内積を計算することで得られます。例えば、全く関係ない(=互いに独立している)ベクトル同士だと直行しているはずで、直行しているベクトルの内積は0になります。逆に0以外であれば正・あるいは負の相関があることになります。そして、正規化(平均0・分散1)した上で相互相関を取ったものが正規化相互相関です。

一応式も書いておきます

SSD(I_1, I_2) = \sum_{[x, y] \in R} (I_1(x, y) - I_2(x, y))^2 \\
C(I_1, I_2) = \sum_{[x, y] \in R} I_1(x, y) I_2(x, y) \\
NCC(I_1, I_2) = \frac{1}{n - 1}\sum_{[x, y] \in R} \frac{(I_1(x, y) - \mu_1)}{\sigma_1} \cdot \frac{(I_2(x, y) - \mu_2)}{\sigma_2}

NCCは、内積を取るという性質上Templateでフィルタをかけているような処理になります。以下は実際に処理してみた例で、Templateに一致する箇所が反応しているのが分かります。

image
CSE/EE486 Computer Vision I, Lecture 7, Template Matching, p7

より厳密なマッチングを行いたい場合は、A->BだけでなくB->Aからもマッチングを行い双方で一致していると判断されたもののみ使うという方法もあります。
この特徴点のマッチングを使用することで、パノラマのような写真を作ったり画像の分類や検索などを行うことが可能になります。

OpenCVでの実装

最後に、OpenCVでの実装方法を紹介しておきます。以下のリポジトリに、Jupyter notebookで書いたサンプルをおいています。

icoxfog417/cv_tutorial_feature

なおOpenCVのインストールですが、Windowsの方はAnaconda(conda)がお勧めです。numpyやmatplotlibはもちろんですが、OpenCV本体も以下から一発でインストール可能です。

menpo/Packages/opencv3

実装に当たっては、以下のOpenCV公式のチュートリアルを参考にしました。

書くコード自体はほんの数行ですが、パラメーターの調整を行わないとうまく検出できないことが多く(特にSIFT)、そしてパラメーターの調整にはやはり理論的な理解が必要です。そういう意味では、本当の意味でOpenCVを使いこなすには理論的な理解は不可欠だと思います。

image

今回ご紹介した解説が、石化を解き真の画像処理マスターとなるための手助けとなれば幸いです。

研究動向

最近はConvolutional Neural Network(CNN)が登場し、画像からの特徴抽出という点では古来からの手法とCNN、どちらがどういいのかと言う点がまず気になると思います。
その点についてのサーベイを、まず紹介します。

CNNはやはり学習が必要な点と処理速度の点でハンデがありますが、様々なタスクを高い精度でこなすことができるという点はやはり強いです。SIFTに代表される手法に含まれる考えは未だ有用なものも多いので、組み合わせによってより高みへ行ける・・・というのが上記の論文で提案されています。

DNNを利用した特徴抽出の研究としては、以下のようなものがあります。

参考文献

3446
3580
7

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3446
3580

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?