Machine Learning Advent Calendar 2015 第14日です。去年のAdvent Calendarで味をしめたので今年も書きました。質問、指摘等歓迎です。
この記事の目的
ここ2~3年のDeep Learningブームに合わせて、リカレントニューラルネットワークの一種であるLong short-term memory(LSTM)の存在感が増してきています。LSTMは現在Google Voiceの基盤技術をはじめとした最先端の分野でも利用されていますが、その登場は1995年とそのイメージとは裏腹に歴史のあるモデルでもあります。ところがLSTMについて使ってみた記事はあれど、詳しく解説された日本語文献はあまり見当たらない。はて、どういうことでしょうか。
本記事ではLSTMの基礎をさらいつつ、一体全体LSTMとは何者なのか、LSTMはどこに向かうのか、その中身をまとめて追っていこうと思います。実装とか華々しいものはないんですが、お付き合いください。付録的に、ILSVRC2015の優勝モデルであるResidual Networksの解説も付けました(第4部)。
目次
本記事は以下のように構成されています。最初の2つが基礎、それ以降は少し込み入った事例になります。お好きなところからどうぞ。あと、長いところは太字を読めばだいたいなんとかなります。
- 第1部:LSTMの基礎
- 第2部:LSTMの構造と学習
- 第3部:応用事例から見るLSTMとその派生アーキテクチャ
- 第4部:RNN≒真に深いネットワーク?
- 第5部:汎用コンピュータとしてのLSTM
- 終章:LSTMを超えて
- まとめと参考文献
本記事は可能な限りわかりやすく説明したつもりですが、通常のニューラルネットワークの誤差逆伝播法による学習について知っているとスムーズです。
第1部:Long short-term memory(LSTM)の基礎
時系列データとその問題
本題に入る前に、時系列データの定義を簡単に述べておきましょう。時系列データとは、ある要素が順番に
x_1, x_2, x_3, ..., x_T
のように並んでいるデータのことを言います。このデータの添え字は通常tで表されますが、このtはデータの種類によって若干意味合いが異なります。時系列データの代表例として音声の波形、動画、文章(単語列)などがありますが、音声の波形なら一定の時間間隔(数ms)でのサンプル時間になりますし、文章なら単語を前から並べたときの番号になります。
時系列データに対する伝統的な問題をいくつか挙げると、
(1) 文章・対話の生成
(2) 音素・音声認識
(3) 映像認識
などが挙げられます。
分量の都合で、ここで詳細を述べるのは避けますが、(1)の文章生成ならば、「今までの単語列を入力として、もっともらしい次の単語を予測する」ことをLSTMが担います。正しい文章を繰り返しLSTMに覚えさせる(重みベクトルを更新する)ことで、このLSTMは"this"の後に"is"が来るようなルールを「事実上」学習します。このシチュエーションにおいては、入力と出力の形式は共に同じです。一方で、(2)の音素・音声認識の場合、**「今までの音声波形(orその特徴量)を入力として、その時点で発話されている音素を予測する」**タスクになります。この場合、入力の波形と出力の音素列の形式に直接の関係性はありません。
LSTMとは?
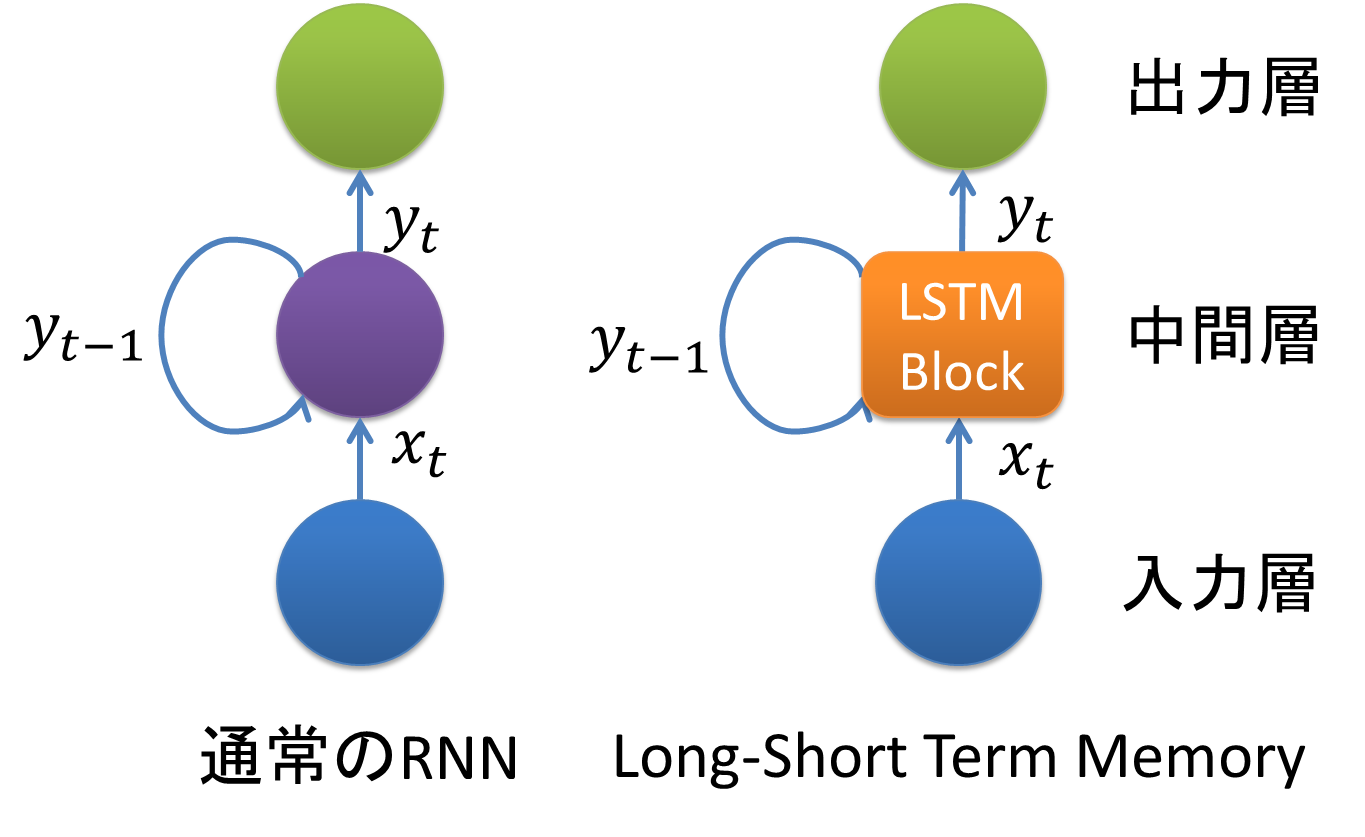
LSTM(Long short-term memory)は、RNN(Recurrent Neural Network)の拡張として1995年に登場した、時系列データ(sequential data)に対するモデル、あるいは構造(architecture)の1種です。その名は、Long term memory(長期記憶)とShort term memory(短期記憶)という神経科学における用語から取られています。LSTMはRNNの中間層のユニットをLSTM blockと呼ばれるメモリと3つのゲートを持つブロックに置き換えることで実現されています。
LSTMのその最も大きな特長は、従来のRNNでは学習できなかった長期依存(long-term dependencies)を学習可能であるところにあります。その最も単純な一例を以下に示します。
( x, a_1, a_2, \cdots , a_{p-1}, x ) \\
( y, a_1, a_2, \cdots , a_{p-1}, y )
例えば、上図のような入力系列を受け取り、次のステップの入力を予測するような学習器を考えます。今回学習する系列は、「$x$または$y$が入力されたのち非常に長いシンボル$a_1, \cdots, a_{p-1} $が続き、その後最初の$x$または$y$が出現する」というものです。この系列を正しく学習するためには、最初の要素の情報を少なくとも$p$ステップ維持する機能を持つようにNNの重みを更新する必要があります。通常のRNNでも数十ステップの短期依存(short-term dependencies)には対応できるのですが、1000ステップのような長期の系列は学習することができませんでした。LSTMはこのような系列に対しても適切な出力を行うことができます。以下に[Hochreiter & Schmidhuber 97]の結果を示します。
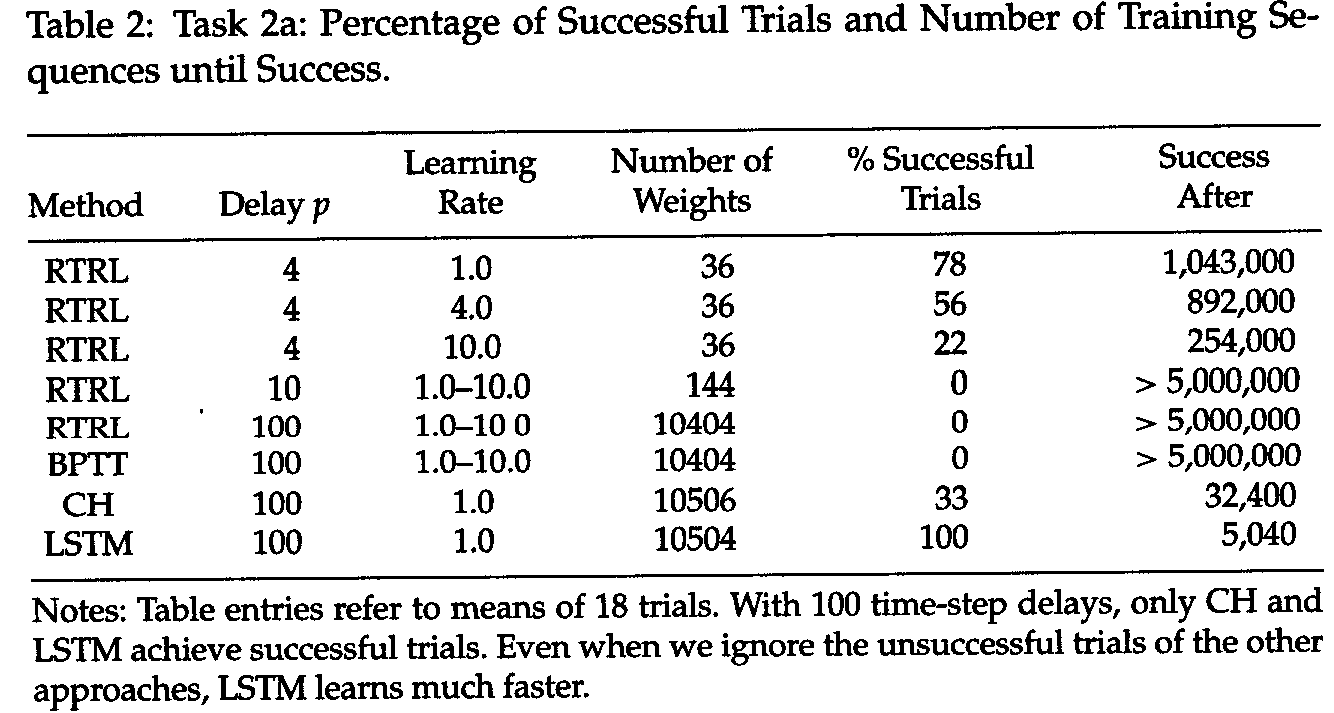
([Hochreiter & Schmidhuber 97]より引用)
上記の実験では100ステップのdelayを学習させていますが、既存のRNN(RTRL、BPTT法を用いた学習)が全く成功していない一方、LSTMでは短い学習時間で確実に学習できています。
背景:Hochreiterの勾配消失問題(91年)
LSTMの構造に深入りする前に、LSTMが考案される前にHochreiterが指摘した勾配消滅(爆発)問題について述べる必要があります。
当時のRNNの学習方法は、BPTT(Back-Propagation Through Time)法とRTRL(Real-Time Recurrent Learning)法の2つが主流でしたが、その2つとも完全な勾配(Complete Gradient)を用いたアルゴリズムでした。しかし、このような勾配を逆方向(時間をさかのぼる方向)に伝播させるアルゴリズムは、多くの状況において「爆発」または「消滅」することがあり、結果として長期依存の系列の学習が全く正しく行われないといいう欠点が指摘されてきました。Hochreiterは自身の修士論文(91年)において、時間をまたいだユニット間の重みの絶対値が指定の(ごくゆるい)条件を満たすとき、その勾配はタイムステップtに指数関数的に比例して消滅または発散することを示しました。これはRNNだけではなく、勾配が複数段に渡って伝播する深いニューラルネットにおいてもほぼ共通する問題でした。LSTMはこの問題に対する有効な対処法の1つとして発明され生き残ってきた、という背景があります。
例えば、単体のユニット$u$から$v$への誤差の伝播について解析してみましょう。ステップ$t$における任意のユニット$u$で発生した誤差が$q$ステップ前のユニット$v$に伝播する状況を考えます。すると、誤差は以下に示すような係数でスケールします。
\frac{\partial v_v (t-q)}{\partial v_u (t)} =
\Biggl\{
\begin{array}{ll}
f'_v(net_v (t-1)) w_{uv} & q = 1 \\
f'_v(net_v (t-q)) \sum_{l=1}^{n} \frac{\partial v_v (t-q+1)}{\partial v_u (t)}w_{lv} & q > 1
\end{array}
$l_q = v$と$l_0 = u$を使用して、
\frac{\partial v_v (t-q)}{\partial v_u (t)} = \sum_{l_1 = 1}^{n} \cdots \sum_{l_{q-1} = 1}^{n} \prod_{m=1}^q f'_{l_m} (net_{l_m} (t - m)) w_{l_m l_{m-1}}
上式を見ればわかるように、
\begin{array}{ll}
| f'_{l_m}(net_{l_m} (t - m)) w_{l_m l_{m-1}} | \; > 1.0 & for\; all\; m
\end{array}
の時、スケール係数は発散し、その結果としてユニット$v$に到着する誤差の不安定性により学習が困難になります。一方、
\begin{array}{ll}
| f'_{l_m}(net_{l_m} (t - m)) w_{l_m l_{m-1}} | \; < 1.0 & for\; all\; m
\end{array}
の時、スケール係数はqに関して指数関数的に減少します。上式の状況はRNNにおいて頻発し、正しい学習を妨げてきました。この議論は容易に全ユニットの誤差の伝播についても拡張することができます。
この問題の詳細は2001年の総説[Hochreiter+ 01]、Hochreiterの元論文[Hochreiter 91](ドイツ語)、Bengioのより突っ込んだ解析[Bengio+ 94]で扱われています。
第2部:LSTMの構造と学習
LSTMは一見複雑で得体のしれない物体に見えますが、その構造は決して難しすぎるものではありません。ただし、複数回の拡張に伴い様々なバージョンが混在しています。今回は、[Greff+ 15]に従い、次の4つの代表形に分けて紹介します。
(1) オリジナル(95,97年)[Hochreiter & Schmidhuber, 95;97]
(2) Forget Gateの導入(99年)[Gers & Schmidhuber, 99]
(3) Peephole Connectionの導入(00年)[Gers & Schmidhuber, 00]
(4) Full Gradientの導入(05年)[Graves & Schmidhuber, 05]
第一世代LSTM(95,97年)
以下に最初のLSTM Blockの構造を示します。オリジナルのLSTMは、上節の勾配消滅問題を強く意識した構造をしています。1つ1つの要素を見ていきましょう。
まず、入力層の出力及び中間層の1ステップ前の(RNNのループ部)の出力は、それぞれ3か所に同時に入力として供給されます。実線が入力層の出力、点線が中間層の1ステップ前の出力を表します。この3か所のうち、下からの入力が実際の入力値として使われ、その他2つは下から「入力ゲート(Input Gate)」、「出力ゲート(Output Gate)」と呼ばれ、入力値及びメモリセル内の状態(State)の制御に使用されます。各入力は重み行列$w_{z, in, out}, R_{z, in, out}$と乗算されたのち加算され、各ゲートの活性化関数を通します。下図の活性化関数の色はその種類を表しており、2つのゲートに関しては常にシグモイド関数が使われます。
Constant Error Carousel (CEC)
CECは、誤差消滅問題に対応するために導入された非常にシンプルなアプローチです。上記の解析から、誤差消滅問題に対応するためには、
f'_{l_m}(net_{l_m} (t - m)) w_{l_m l_{m-1}} = 1.0
を満たせば、事実上無限時間であっても誤差は正しく伝播します。途中の式変形は省きますが、結果として、中央のメモリセルの状態$s_{c_j}(t)$は、
\begin{align}
s_{c_j}(0) = 0, \; s_{c_j}(t) = s_{c_j}(t-1) + y^{in_j}(t) g(net_{c_j}(t)) & \; for \; t > 0
\end{align}
という重み係数1(線形)による和によって簡単に表現されます。これがCECのミソです。
入力ゲートと出力ゲートの意味
CECが誤差消失問題を解決することはわかりました。では、同時に導入された入力ゲートと出力ゲートはどのような意味を持つのでしょうか。これは、定性的な分析から導き出すことができます。
入力重み衝突(input weight conflict)
一般のRNNを考えたとき、ユニット$i$からの入力は、重み$w_{ji}$を与えられてユニット$j$に入力されます。誤差逆伝播法を用いる場合誤差信号がユニットを遡り、必要な場合重み$w_{ji}$を更新します。ところが、時系列データを学習する場合$w_{ji}$は次の矛盾する重み更新を同時に受ける場合があります。
- ユニットjを活性化されることによる入力信号の伝達
- ユニットiからの無関係な入力によってユニットjの値が消去されることを防ぐ入力信号の保護
1.は例えば、先の例に挙げた系列において、$x$が入力されたことを示す情報を次々に未来のユニットに伝達するために$w_{ji}$の値を大きくする場合を指します。一方で$a_1, \cdots, a_{p-1}$といった無関係な入力を受けてユニットの値が更新されても困るので、2.のように$w_{ji}$の値を小さくしたい場合もあります。従来型のRNNではこのような矛盾する重み更新が頻発し、学習を遅らせる主要な要因となっていました。
そこで、LSTMでは入力ゲートを導入し、追加の重みパラメタを持たせることで、「前のユニット(1つ前の時間のユニット)の入力を受け取るか否か」を判断させるようにしました。そうすることで必要に応じて誤差信号の伝播をゲート部で止め、必要な誤差信号だけが適切に伝播するようにゲートを開いたり閉じたりするのです。これが入力ゲートと呼ばれたる由縁です。
出力重み衝突(output weight conflict)
出力ゲートも入力ゲートと同様に、以下の理由による重みの衝突を防ぐために導入されています。ユニット$j$の情報が重み$w_{kj}$に従いユニット$k$に出力を行うことを考えると、次の2つの衝突が起きます。簡単ですね。
- ユニットkを活性化されることによる出力信号の受信
- ユニットjからの無関係な出力によってユニットkの値が消去されることを防ぐ出力信号の保護
ここまでが第一世代LSTMの概要になります。他にもRNNにまつわるさまざまなとその対処が述べられているのですが、それについては元論文や次の記事を参照してください。
Forget Gateの導入(99年)
さて、複数の時系列タスクにおいて目覚ましい成果を上げた初代LSTMですが、内部メモリセルの更新は線形で、その入力を貯め込む構造であったため、例えば、入力系列のパターンががらりと変わったとき、セルの状態を一気に更新する術がありませんでした。そこで、99年の拡張で忘却ゲート(Forget Gate)が導入されました。
忘却ゲートは、誤差信号を受け取ることで、一度メモリセルで記憶した内容を一気に「忘れる」ことを学習します。そうすることで、状態遷移が起こり、今までの記憶が不必要になった時点で素早くセルを初期化することを可能にしました。忘却ゲート部の数式はこれで
s_{c_j}(t) = y^{forget_j}(t)s_{c_j}(t-1) + y^{in_j}(t) g(net_{c_j}(t))
のように書き表すことができます。
忘却ゲートを導入した元論文[Gers+ 99]の解説を発見したので、併せて参照ください。
Peephole Connectionの導入(00年)
忘却ゲートを導入して一見完成に見えたLSTMですが、ゲートの制御に関して次の致命的な問題を抱えていました。
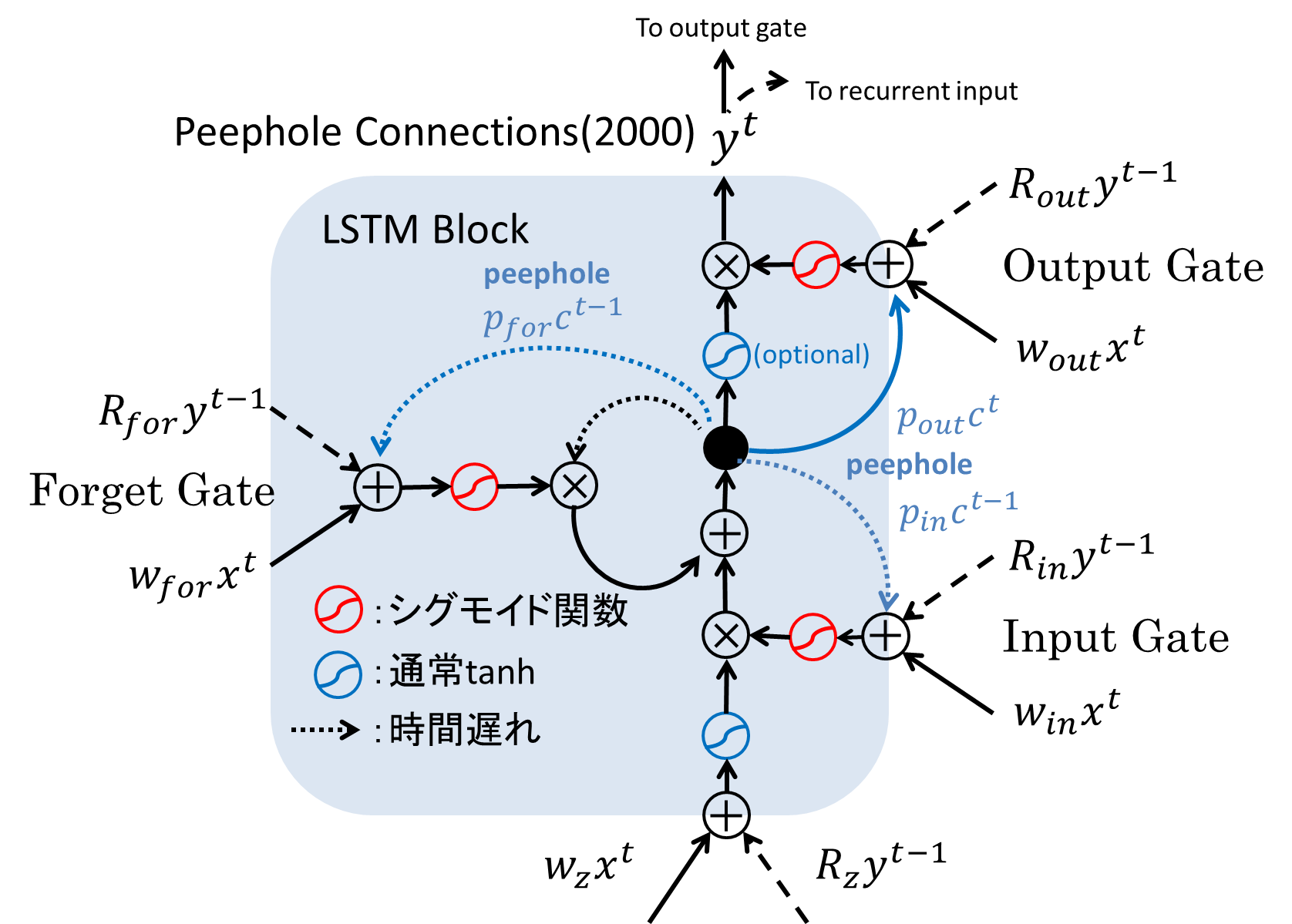
そもそも、3つの制御ゲートの役割は、「メモリセルの内容を書き換えるか/忘れるか/出力するか」ということにありました。ところがこれまでのLSTMでは、そのゲートの制御はLSTMの外側と呼べる(1)入力層の出力(2)中間層の1ステップ前の出力をベースとして行われており、制御対象であるメモリセル自身の内部状態は制御に利用されていない状態でした。例えば、一見すると中間層出力である$y^(t-1)$がメモリセルの情報をすべて含んでいるように見えますが、出力ゲートが出力を遮断している($\simeq 0$)場合メモリセルの真の状態は隠ぺいされてしまいます。そこでpeephole connectionと呼ばれる接続をメモリセルから各ゲートに流し込むことで解決を図りました。下図の青い矢印に注目してください。
また、中央上側のOutput Activation Functionは、性能に明確な影響を及ぼさないという理由で排除されることがあります。現在はこのバージョンが事実上LSTMの標準形とみなされていますが、タスクによって細かい修正は適宜行われています。
補足:chainerはどのLSTMを使っている?(15/12/14時点)
PFI発のNNフレームワークであるchainerには1行で追加できる非常に便利なLSTMが提供されていますが、このLSTMはどのバージョンにあたるのでしょうか?実装を見てみましょう:
見ると、chainerのLSTMは99年版の忘却ゲート付きのLSTMを採用しているようです。Peephole Connectionは導入されていません。また、学習方法も後述のFull BPTTではなく、01年時点での方法であるBPTT法とRTRL法のミックスになっています。後述の検証では、Peephole Connectionの導入によるパフォーマンスには大きな影響はないとされていますが、使用にあたってはやや注意が必要と思われます。
Full BPTTによる学習(05年)
LSTMの構造は00年にひとまずの完成を見ましたが、その学習方法は昔ながらの手法であるRTRL法とBPTT法を混合し、時間方向への誤差逆伝播には一部の変数の勾配しか使用しないという、やや特殊な学習方法でした。[Graves & Schmidhuber, 05] では学習をBPTT(Back-Propagation Through TIme)法の枠組みに沿って統一的に定式化することでより明快で実装しやすいものになりました。次節では05年バージョンに沿ってLSTMの具体的な数式を見ていきます。
LSTMの順伝播計算
さて、長々と説明を書いてきてようやくLSTMを定式化できるようになりました。00年版の図を見ながら式を見ていってください。順伝播の計算は以下のようになります:
\begin{align}
\bar{z}^t &= W_z x^t + R_z y^{(t-1)} + b_z \\
z^t &= g(\bar{z}^t) \\
\bar{i}^t &= W_{in} x^t + R_{in} y^{(t-1)} + p_{in} \odot c^{t-1} + b_{in} \\
i^t &= \sigma(\bar{i}^t) \\
\bar{f}^t &= W_{for} x^t + R_{for} y^{(t-1)} + p_{for} \odot c^{t-1} + b_{for} \\
f^t &= \sigma(\bar{f}^t) \\
c^t &= i^t \odot z^t + f^t \odot c^{t-1} \\
\bar{o}^t &= \sigma(W_{out} x^t + R_{out} y^{(t-1)} + p_{out} \odot c^t + b_{out}) \\
o^t &= \sigma(\bar{o}^t) \\
y^t &= o^t \odot h(c^t) \\ \\
但し、\ \ \sigma(x) &= sigmoid(x) = \frac{1}{1 + e^{-x}}, \\ g(x) &= h(x) = tanh(x)
\end{align}
後半の式の計算には前半の式の計算結果が要る場合があるので計算順には注意が必要です。また、$\odot$はpointwise multiplication(要素ごとの積)を意味します。
また、peephole connectionへの入力は、入力・忘却ゲートに関しては1ステップ前、出力ゲートのみ現在のステップの状態が供給されるところにも注意してください。
最適化したい重みは15変数になります。
- 入力重み:$W_z, W_{in}, W_{for}, W_{out} \in R^{N×M}$
- リカレント重み:$R_z, R_{in}, R_{for}, R_{out} \in R^{N×N}$
- peephole重み:$p_{in}, p_{for}, p_{out} \in R^N$
- バイアス重み:$b_z, b_{in}, b_{for}, b_{out} \in R^N$
LSTMの逆伝播計算
LSTMの逆伝播が難しく見えるのには、(1)1ステップ未来のループから誤差信号が来る(2)複数のゲートがあり、伝播の順番がわかりにくい という2つの理由がありますが、これも丁寧に数式を追っていけば難しくありません。
まず、LSTMの中身は忘れて、ステップ(時間)tにおける入力$x_t$、出力$y_t$を考えましょう。まず、出力層で得た誤差信号が遡ってきて、$\Delta^t = \frac{\partial E}{\partial y^t}$が与えられます。LSTM内部ではこの$\Delta^t$を元手に誤差が伝播して、最終的に$\delta x^t = \frac{\partial E}{\partial x^t}$を計算して入力層へ遡ります。このような$\delta ?^t$を計算するには、順伝播の時にその中身を伝播させたすべての接続からの誤差信号の和を計算していきます。式を見ていきましょう。
\begin{align}
\delta y^t &= \Delta^t + R_z^T \delta z^{t+1} + R_{in}^T \delta i^{t+1} + R_{for}^T \delta f^{t+1} + R_{out}^T \delta o^{t+1} \\
\delta o^t &= \delta y^t \odot h(c^t) \odot \sigma'(\bar{o}^t) \\
\delta c^t &= \delta y^t \odot o^t \odot h'(c^t) + p_{out} \odot \delta o^t + p_{in} \odot \delta i^{t+1} + p_{for} \odot \delta f^{t+1} + \delta c^{t+1} \odot f^{t+1} \\
\delta f^t &= \delta c^t \odot c^{t-1} \odot \sigma'(\bar{f}^t) \\
\delta i^t &= \delta c^t \odot z^t \odot \sigma'(\bar{i}^t) \\
\delta z^t &= \delta c^t \odot i^t \odot g'(\bar{z}^t) \\
\end{align}
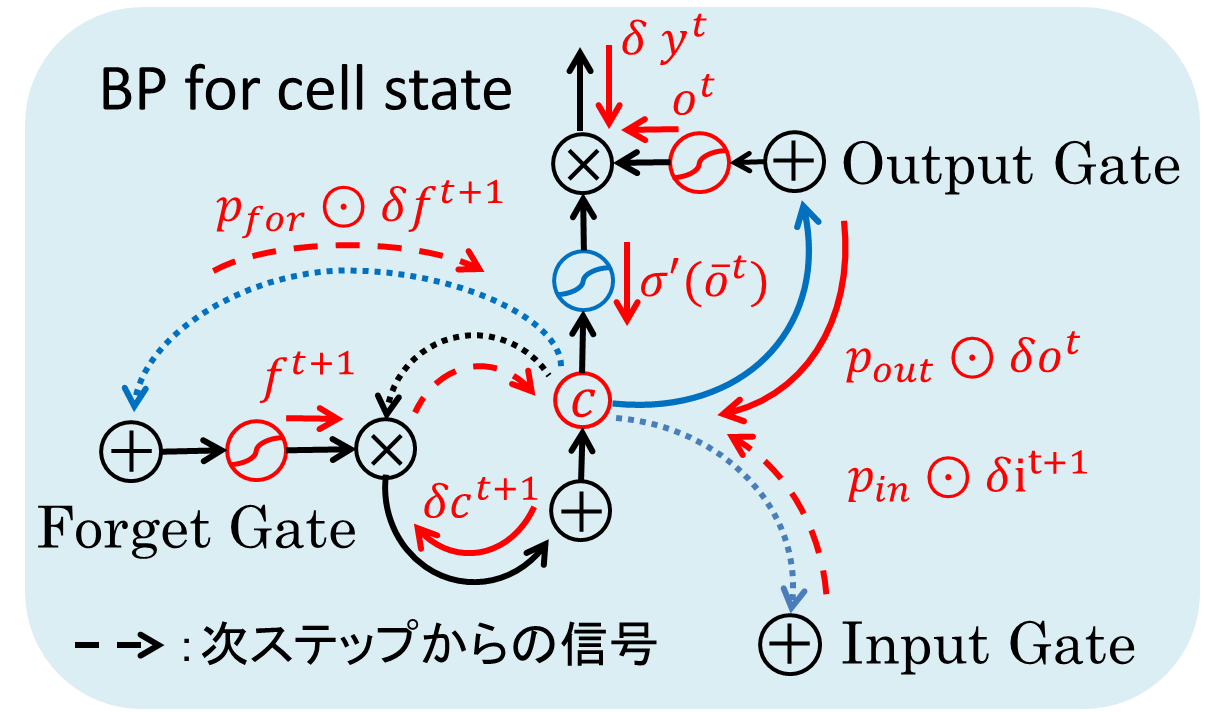
式だけではなんともわかりにくいですね。中央のメモリセルのデルタである$\delta c^t$に絞って見てみましょう。
中央のメモリセルに向かって、5か所の赤い矢印が進んできています。これが順伝播させた項からやってきた$c^t$への誤差信号です。内訳は第1項から順に
- LSTM Blockの出力$y^t$からの誤差
- 出力ゲートからの誤差
- 未来の入力ゲートからの誤差
- 未来の忘却ゲートからの誤差
- 未来のセル自身からの誤差
となります。そして、計算済みの各デルタは次の操作によって計算されます。
- 通常の乗算を通るたびにその項で乗算(例えば、第1項の$o^t$)
- 非線形関数を通るたびにその微分を乗算(例えば、第1項の$h'(c^t)$)
あとは簡単ですね。式を追っていけばわかると思います。
最終的に、上記のデルタが得られたところで、入力層へのデルタ及び実際に更新したい重みの勾配$W_\star, p_\star, R_\star, b_\star$を計算します($\star$にはz, in, out, forのいずれかが入る)。
\begin{align}
\delta x^t &= W_z^T \delta z^t + W_{in}^T \delta i^t + W_{for}^T f^t + W_{out}^T \delta o^t \\
\delta W_{\star} &= \sum_{t=0}^T \delta \star^t \times x^t \\
\delta R_{\star} &= \sum_{t=0}^{T-1} \delta \star^{t+1} \times y^t \\
\delta b_{\star} &= \sum_{t=0}^T \delta \star^t \\
\delta p_i &= \sum_{t=0}^{T-1} \delta c^t \odot \delta i^{t+1} \\
\delta p_f &= \sum_{t=0}^{T-1} \delta c^t \odot \delta f^{t+1} \\
\delta p_o &= \sum_{t=0}^T \delta c^t \odot \delta o^t
\end{align}
ふー長かった。$\times$は外積を表します。
LSTMの学習のコツ
LSTMを標準的なSGD(Stochastic Gradient Descent、確率的勾配降下法)で学習することを考えましょう。すると、以下のパラメータの設定が必要になります。
- 隠れ層のLSTM Blockの個数
- 学習率
- モーメンタム
- BPTTの打ち切りステップ数(Truncated BPTT)
- 勾配の絶対値のクリッピング(Gradient Clip)
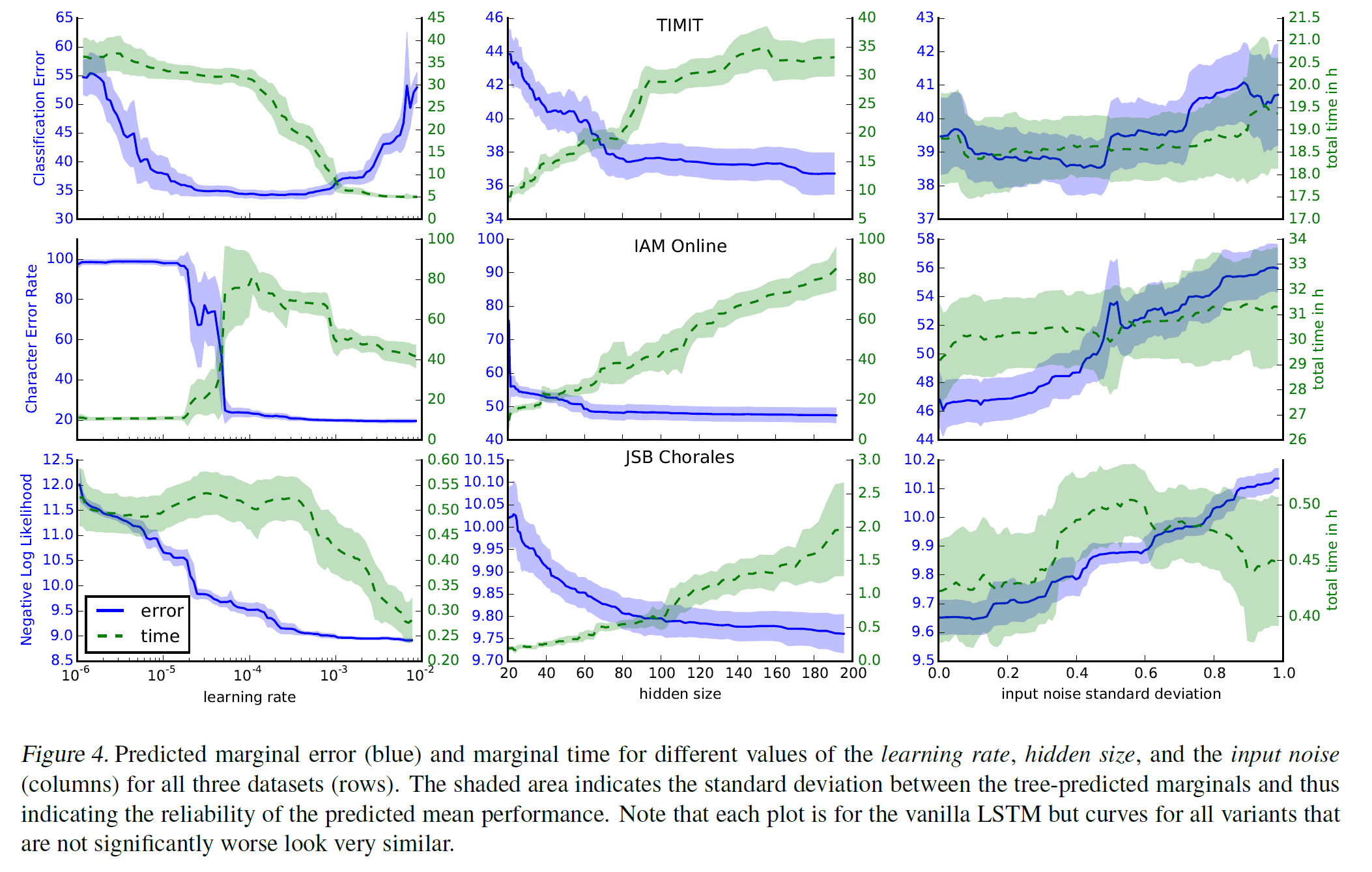
LSTMは先に述べた計算安定性ゆえに適当なパラメタでも学習してるように見えてしまうのですが、実際どのようにパラメタを決めるのが良いのでしょうか?[Greff+ 15]の詳細な分析を少しだけかじって紹介します。下図は3つのタスクにおいて、「学習率」「隠れ層のブロック数」「入力に対するノイズの添加」のパラメタの変化に応じた予測誤差・実行時間の推移を表します。ノイズ添加以外の2つについて、列毎(パラメータ毎)に見てみましょう。
まず、学習率の設定は何においても重要になります。データセットによって大きく傾向が異なりますが、予測誤差が一気に改善する特異な地点が存在することがわかります。論文中ではまず高い学習率(1程度)から始めて、性能の改善が停止するたびに10で割る大雑把な探索が推奨されています。
一方で、隠れ層の数については非常にわかりやすい傾向が出ています。期待通り、隠れ層の数を増やせば増やすほど性能は改善しますが、そのトレードオフとして実行時間が増加します。なお、図表に示されてはいませんが、モーメンタムの値は今回の解析では値の設定による性能の変化はなかったと報告されています。BPTTの打ち切りステップ数についての言及はこの論文ではありませんでしたが、直感的には獲得したい長期依存の長さとタスクの実行時間とのバランスを取るのが標準的な戦略だと思われます。
RNNと勾配のクリッピング(Gradient Cliping)
LSTMはゲートの導入によって勾配「消滅」問題に対応しましたが、厳密には勾配「爆発」問題には対応していませんでした。そこで、2010年頃から勾配のノルムに対して一定の制約値(hard constraint)を設け、ミニバッチの学習毎に大きくなりすぎた勾配のノルムを補正するという方法が取られるようになりました。[Pascanu+ 12]において、BengioらのチームはRNN($\neq$ LSTM)における勾配爆発問題が起こる必要条件がリカレント重み行列$W_{rec}$の最大の特異値にあることを証明し、その明快な回避方法として以下のアルゴリズムに従う勾配クリッピングを正式に提案しました。
\begin{align}
1. \quad & \hat{g} \leftarrow \frac{\partial \epsilon}{\partial \theta} \\
2. \quad & if \quad ||\hat{g}|| \geqq threshold \quad then \\
& \qquad \hat{g} \leftarrow \frac{threshold}{||\hat{g}||} \hat{g} \\
& end if
\end{align}
一瞬おっかなく見えますが、平たく言えば更新の度に $-threshold < ||gradient|| < threshold$ を保証すればよいということです。[Pascanu+ 13]ではthresholdの値についても緩い提案を行っており、多数の更新が行われたときの重み$W_{\star}$のノルムの平均を観察することを推奨しています。彼らは、得られた平均の0.5倍~10倍の値を設定することで(収束速度の差はあれど)大よそ収束すると報告しています。興味深いのは、この提案はBPTT法によって学習する一般のRNNに適用できる勾配消失/爆発問題への対処法を提示しているということです。興味のある方は原論文を参照ください。
LSTMのどの部分が重要なのか?
[Greff+ 15]の分析ではLSTMのどの部分が性能向上に寄与しているかの仔細な分析を行っています。その手法自体は明快で、入力/忘却/出力ゲート・活性化関数・peepholeなど8種類の要素をそれぞれ取り除いた場合の性能低下を計算し、比較することで実現しています。実験の結果、
- 忘却ゲート、出力時の活性化関数の排除による性能低下が最も大きい
- 音楽・言語モデリングにおいては入力ゲートの排除、入力時の活性化関数の排除による影響も大きい
ことが主に示されています。
Connectionist Temporal Classification(CTC)法[Graves+ 06]
これは概要のみを述べるに留めます。詳しくは機械学習プロフェッショナルシリーズの『深層学習』などを参照してください。
LSTMには、1つの入力に対して必ず1つの出力があるという強い制約があります。しかしながら、音声認識などでは、(1)音声信号の系列数と(2)取り出したい音素の系列数は全く異なります。特に、音声認識のように出力の区切りが事前知識から得にくい場合は単純な方法では解決できません。これを解決するのがConnectionist Temporal Classification(CTC)法です。
CTC法は、目標出力ラベル(例えば、"a","i","u"など)に加えて空白ラベル"_"を導入し、出力したい系列("aui")に対して同義の長い冗長な入力("a____u___i__")を対応させることで入力の長さと出力の長さの整合性を取ります。素朴に計算すると計算量が非常に大きくなりますが、HMM(隠れマルコフモデル)の前向き・後ろ向きアルゴリズムと同様のアプローチでこの問題を解決しています。
また、自然言語処理の分野ではsequence to sequence learningと呼ばれる方法があり、入力文の単語数と出力の単語数が一致していなくても対応できるような学習法がよく使われています(後述)。
第3部:応用事例から見るLSTMとその派生アーキテクチャ
95年時点で既に洗練されたアーキテクチャを持っていたLSTMですが、限られたマシンパワーに加えてNN冬の時代にぶち当たって当時はあまり注目されませんでした。実タスクに適用されはじめるのは登場から10年経った05年ごろからになります。初めは音素認識・手書き文字認識でのプロトタイピングが中心でしたが、Deep Learningのブームと共にあっという間に実用レベルの研究が進展し、現在では
- 大規模音声認識(Google)[Sak+ 14]
- 英語-フランス語翻訳(Google)[Sutskever+ 14]
- テキスト読み上げ(Microsoft)[Fan+ 14]
- Google Voice[Sak+ 15]
- 画像からのキャプション生成(Google)[Vinyals+ 14]
- and more...
など多くの領域・企業で利用されています。しかしこれらの学習器の多くはLSTMをそのまま使ってはいません。LSTMの大きな特長として、LSTM blockの改変や積み上げが容易ということがあります。そのため、タスクに応じてLSTMの派生形ともいえる様々な形態が存在します。そのうちのいくつかを眺めてみましょう。
音素・音声認識とBidirectional LSTM(BLSTM)[Graves & Schmidhuber 05][Graves+ 13]
SchmidhuberらはLSTMの初期の応用例の1つとして「フレーム単位音素認識」を選択しました。これは、先のCTC法において指摘した「入力長と出力長の不一致」を認めつつ、まずはフレーム毎の予測を行ってみようという現在の水準から見るとやや難易度の低いタスクです。しかし当時は挑戦的な課題として音素認識は挙げられており、この論文ではその課題を**Bidirectional(双方向) LSTM(BLSTM)**と呼ばれる方法で解決しました。
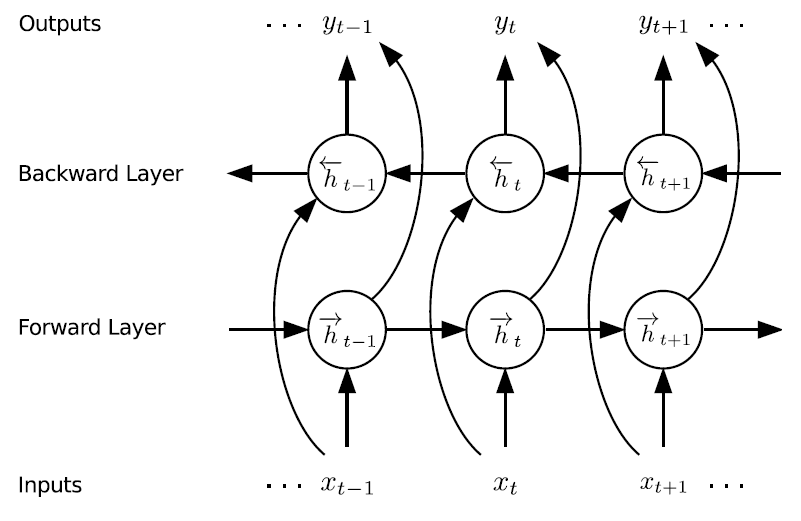
BLSTMの発想は至って単純です。LSTMは、通常「現在までの入力から未来の出力を予測する」モデルですが、これに「未来の入力から過去の出力を予測する」逆方向のモデルを考え、その出力を同一の出力層に統合します。下図にBLSTMの模式図を示します。
この構造の効用は明快です。前提として「認識前にすべての系列情報が手に入っている」という条件がありますが、その分増したコンテクストをより明快に掴むことができます。[Graves & Schmidhuber 05]では、有名なコーパスであるTIMITコーパスを用いて184発話を訓練、BLSTM、LSTM、RNNに関して比較を行いました。その結果を以下に示します。
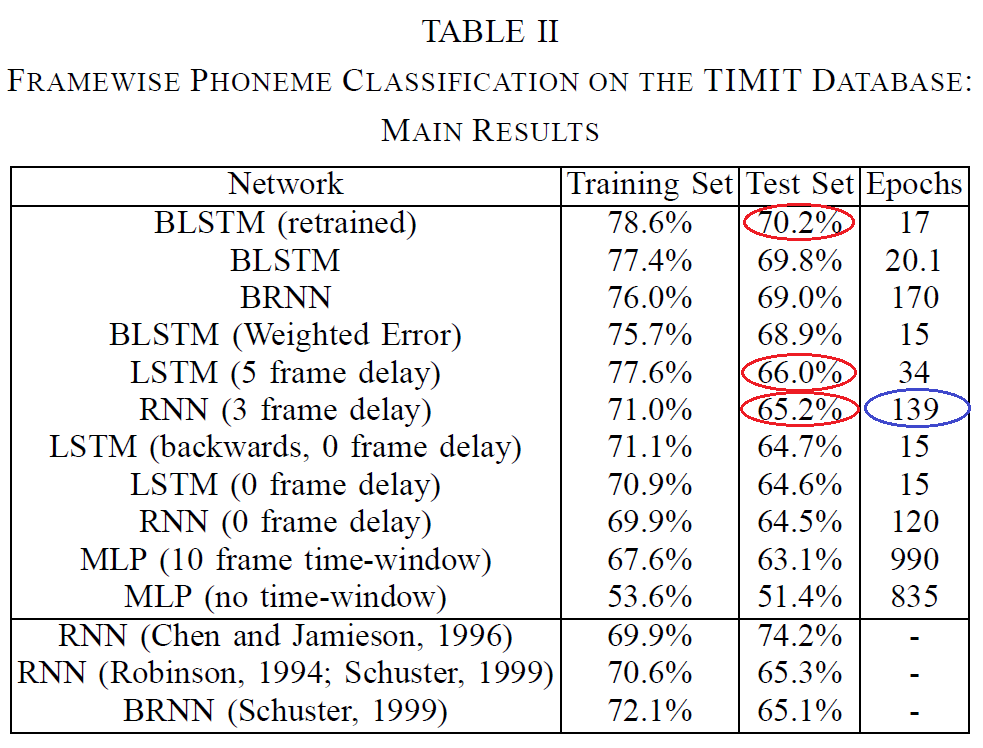
([Graves & Schmidhuber 05]より引用、赤丸・青丸は筆者注)
この論文では僅差となっていますが、RNNに対してLSTM、それもBLSTMの方が結果が高いと出ています。この数字をどう捉えるかは難しいところですが、論文中ではLSTMの方が学習速度が速く、訓練データに対する適応度はRNNを大きくしのいでいた(つまり、データ量を増やせば精度がさらに上がる)ことを僅差の理由として挙げています。この時点ではまだ音声認識の主流モデルであったHMMとの比較はなされていませんが、近年はHMMを大きく凌ぐ成果が多数出ています。
Sequence-to-sequence learningによる機械翻訳[Sutskever+ 14]
LSTMの応用事例として最も面白いのはやはり機械翻訳だと思われます。Sutskeverらは、今までのLSTMの視点に留まらない新しい学習の枠組みを考えました。
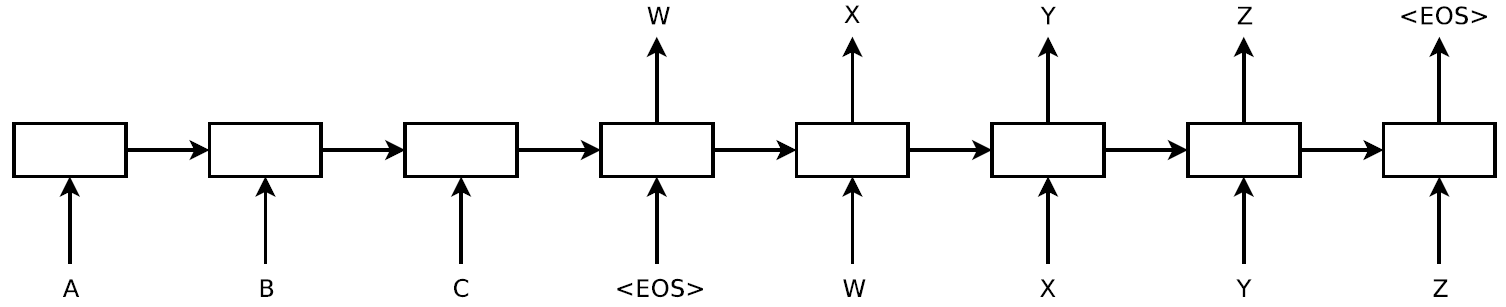
上で紹介したCTC法は、確かに入力と出力の長さが違うような一般的な問題設定の解決をもたらしました。しかし、強い制約として、入力列と出力列の順番に単調な順序関係を要求するという性質がありました。英語と日本語の語順が異なるのは周知のとおり、機械翻訳の問題はCTC法では解決されませんでいた。そこで、Sutskeverは以下のような系列を予測する問題としてLSTMを用いた定式化を行いました:
上図はRNNを時間展開したような模式図です。中央の四角がLSTMを表すと考えて差支えありません。まず、翻訳元の言語ABCを入力して、翻訳元の文章の表現を一括学習します。そして、そののちにこのLSTMは翻訳先の言語の**「次の単語」を予測するタスクを解きます。予測した結果は次のステップの入力として供給されます。こうすることで、機械翻訳のような、入力と出力の長さ及びその語順すらも異なるようなモデルを効率よく学習することができるようになりました。
また、本モデルではLSTMを多段に(4層)積み上げています。そうすることで、文章間の短い相関関係、長い相関関係を別々のレイヤーで掌握することができる**と考えられています。LSTMを積み上げる(Stacked LSTM)発想は現在ではごく当たり前に用いられています。結果として、本論文のモデルは従来のモデルの最高性能に匹敵する結果(翻訳の良さの指標であるBLEUで36.5)をたたき出しました。
尚、機械翻訳については以下の記事で実装まで含めて非常にわかりやすく紹介されているので、詳しくは以下を参照ください。
ChainerとRNNと機械翻訳
第4部:RNN≒真に深いネットワーク?
現在、Deep Neural Networkと言えば、3層の多層パーセプトロンに対して、4層以上の多数の層を組み合わせたフィードフォワードネットワークのことを指すことが多いようです。画像認識分野においては、性能向上を目的として、Alexnet(8層、2012年)、VGGNet(16または19層、2014年)、GoogLeNet(22層、2014年)、と年を追うごとにその層数を増加させてきました。しかし、層をやみくもに増やせば学習精度が向上するわけではなく、緻密なアーキテクチャの構築によって層数の増加、精度向上が図られました。
一方でRNNを振り返ってみましょう。RNNそのものの構造は自己への閉ループを1つ持つだけの単純な構造をしていますが、これを時系列方向に展開するとその総数は時系列の長さ$T$に比例します。当然多くの時系列データは1000ステップ以上の長期のステップを扱うわけなので、素朴には昔ながらのRNNの方が深い層数を扱っていると言えます。
LSTMは、解釈によっては非常に深い層数のネットワークともとれるRNNに対して勾配が消失しない方法を考え、深いネットワークにおける問題を克服しました。今年、そんなLSTMにインスパイアされたようなモデルが立て続けに提案されました。LSTMからいったん離れて、これらのモデルを見ていきましょう。
Highway Networks[Srivastava+ 15]
Highway Networks(以下、HN)は、LSTMの重要な要素技術であるゲートを導入することで100層以上の深いネットワークを学習可能であることを示しました。著者にはLSTMの生みの親であるSchumidhuberが入っており、LSTMの影響を強く受けています。
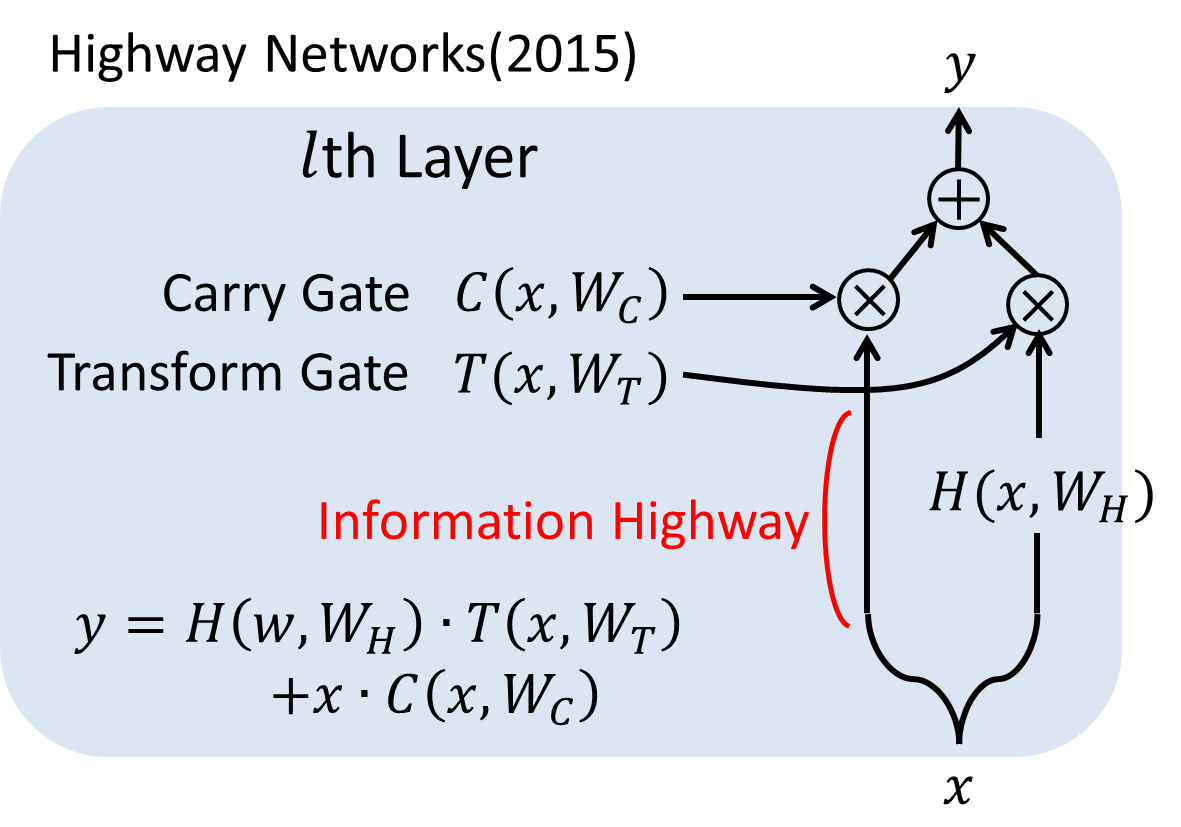
下図にHNの1レイヤーの構造を示します。
通常のフィードフォワードネットワークでは、1レイヤーの入力と出力は本質的には下式のように表されます(バイアス項などは省略):
y = H(x, W_H)
この変換Hは通常の非線形変換でも、CNNにおける畳み込み、リカレント構造などでも構いません。一方、HNでは、Transform GateとCarry Gateの2つのゲートを新たに導入し、以下のような計算を行います。
y = H(x, W_H)・T(x, W_T) + x・C(x, W_C)
見て分かるように、Transform gateは変換された出力をどれだけ伝播するか、Carry gateは未変換の入力をどれだけ運ぶかを表します。簡単のために、論文中では$C=1-T$として、学習時には$H$と$T$2つの変換の最適化を行うことで学習します。T、C共に非線形のシグモイド関数による変換を挟んで、0~1の間の数値を取るようになっています。
通常、深いネットワークの重みを変更したい場合、100層なら100層先まで順番に重みを変化させていくしかありません。すると、少ない層数の時と比べて必ずその伝播は遅くなり、層数の増加につれてその影響は深刻になります。しかし、Carry Gateによる"Information Highway"を用意することでHNでは高速な情報の伝播を実現しました。
Highway Networksの初期化と学習
HNの学習は非常にシンプルです。まず、Transform Gateのパラメータの初期値$T(x) = \sigma (W_T^T x + b_T)$の$b_T$の値には負の値(-1, -3など)を与えておきます。これはCarry Gate(恒等変換)の方に初期の重要度を与えることを意味し、これにより初期の誤差が速く浅い層に伝播するとされています。最適化はシンプルにSGD(確率的勾配降下法)及びmomentum(モーメンタム)を使用していますが、1000層のネットワークでも破たんすることなく学習したとされています。
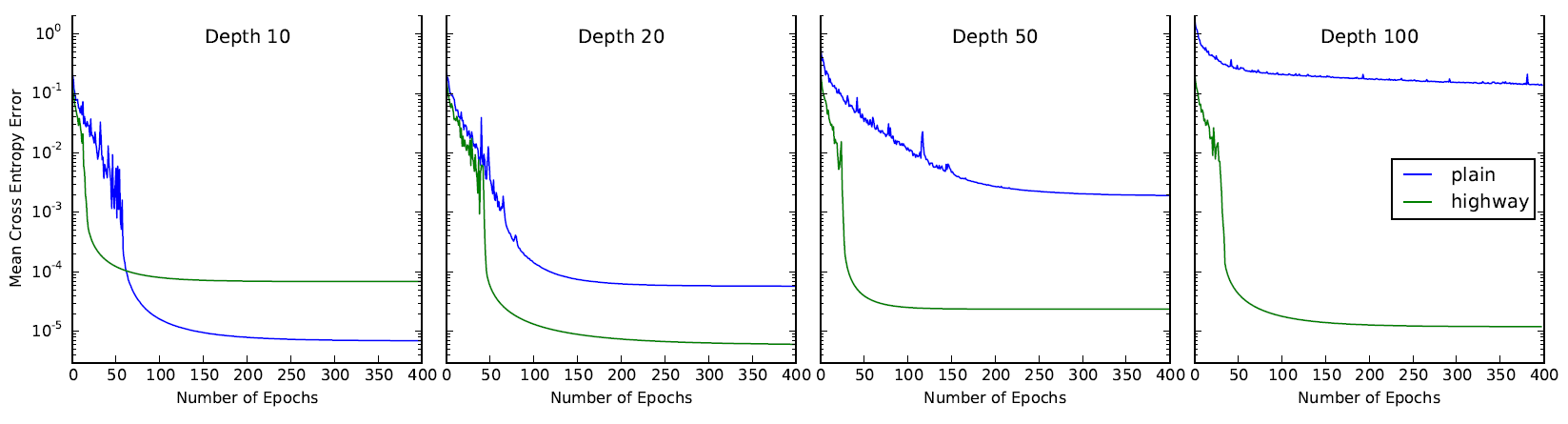
特筆すべきは深いネットワークにおけるその収束の速さで、下図からは20層以上のネットワークにおいて高速に、よく汎化していることが確認できます。
Deep Residual Networks[He+ 15]
つい先日ILSVRC 2015で優勝を飾った最新のモデルです。2位以下を大きく突き放してImageNetのTest Setにおいて**エラー率3.57%**を叩き出しました。さらには、そのネットワークが152層にも及んでいることが判明し、大きなインパクトを与えました。このモデルの中身を見てみましょう。
Residual Learning
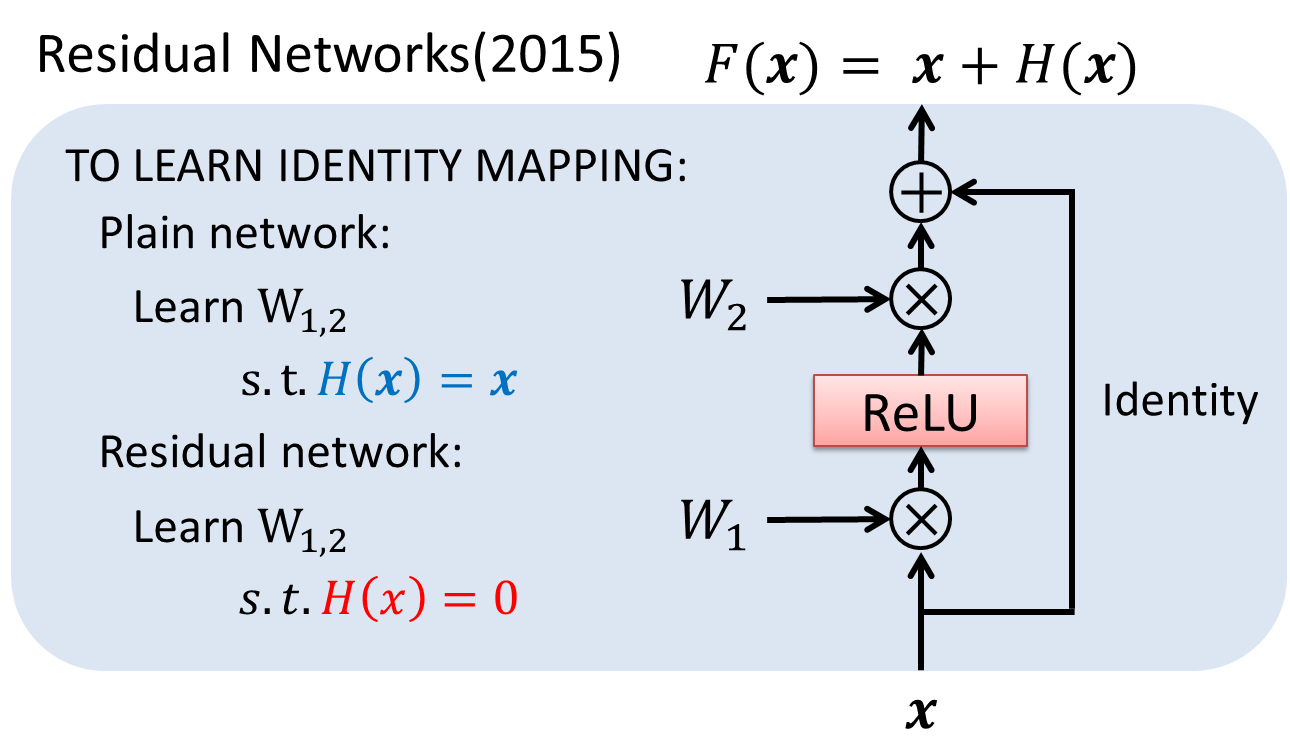
Deep Residual Newtorks(ResNet)の発想はHNのそれと非常に似ています。が、その中身はHNよりさらにシンプルな構成となっています。HNではゲートの開閉により変換を挟んだ出力と無変換の出力の土合を調整したのに対し、ResNetでは各レイヤーにレイヤーの変換を飛び越すような恒等変換を加算します。以下にその模式図を示します。
ResNetのレイヤーは、入力として$x$を受け取り、出力として恒等変換された$x$と変換が施された$H(x)$の和である$x+H(x)$が返されます。そのため、ある変換$H(x)$を学習することは、所望の出力$F(x)$と入力$x$の残差(Residual)を目的の値に近づけることと解釈することができます。論文中ではこの$F(x)$をResidual Functionと呼んでいます。一見何とでもない変換に見えますが、これがDNNにおいて避けられない事象であるdegradation problemを解決する突破口となります。
DNNは、NNの層を増やし段階的に特徴を取り出すことによって圧倒的な表現力を達成してきましたが、層を追加するにつれ、その学習は難しくなります。現在ではそのような認識は当たり前に見えますが、理想的には深いネットワークは浅いネットワークの上位互換であるべきです。なぜそれが達成できないのか。解析の結果、層数を増やすとかえってエラー率が上がる有力な原因として、"degradation problem"という現象が発見されました。この問題は、深いネットワークが、余計な(これ以上の精度向上を望めない)レイヤーに関して恒等写像を学習するのが難しいという状況を引き起こすことで起こります。数多くの非線形変換を組み合わせるDNNでは、恒等写像を再現する方がかえってネックになっていたのです。
そこでResNetでは恒等写像を学習する過程を非常に簡単に行う方法を考えました。入力そのものとの残差を取るのです。すると、今まで$H(x)=x$となるような最適化が必要だったところ、$H(x)=0$を学習するだけで済むようになりました。もちろん、ネットワーク全体としては必ずしも恒等写像を学習することが目標ではありませんが、この変換によってネットワーク全体の最適化が容易になったと報告されています。
Deep Residual Networksの構成と学習
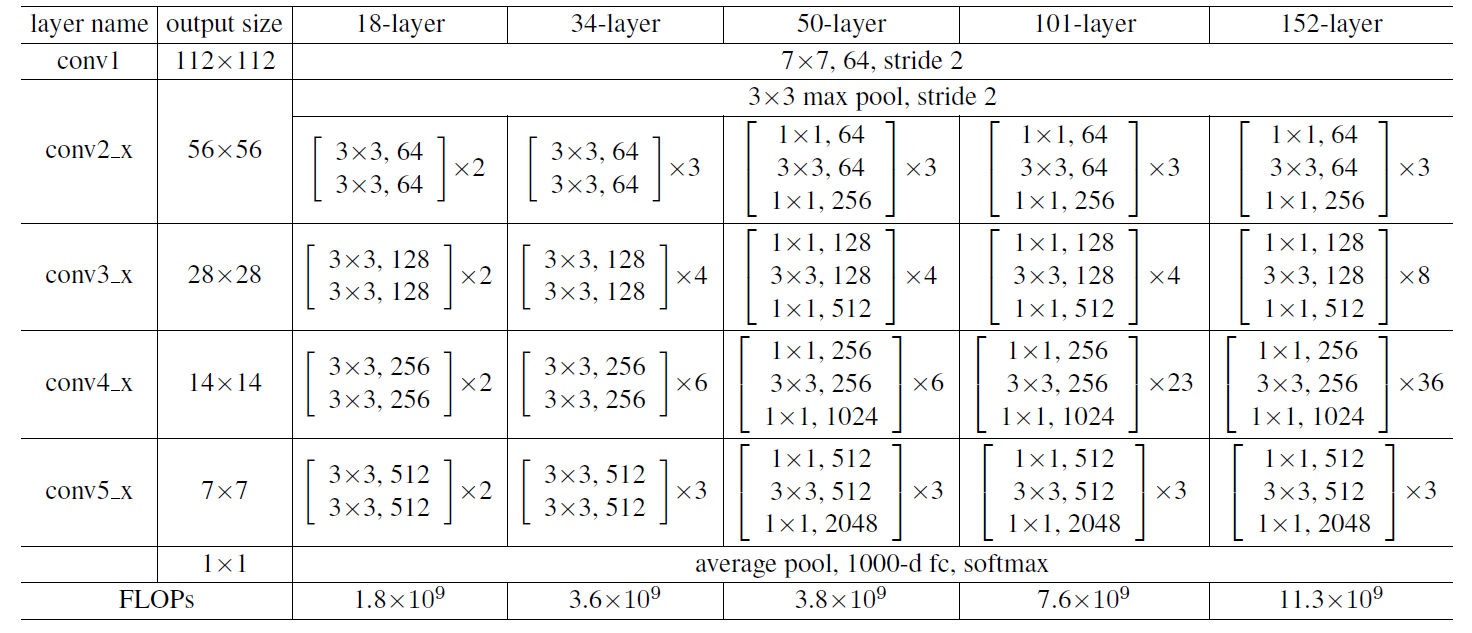
ResNetの構成もHNの構成と同様、GoogLeNetなどと比べると非常にすっきりしています。ImageNetの画像入力サイズは224×224ですが、これに5種類の大きさの畳み込み層(conv)+バッチ正規化(Batch Normalization)を用意したうえで、それらを合計の層数によって数を変えて構成しています。以下の図は18, 32,4, 50, 101, 152層のアーキテクチャを示しています。
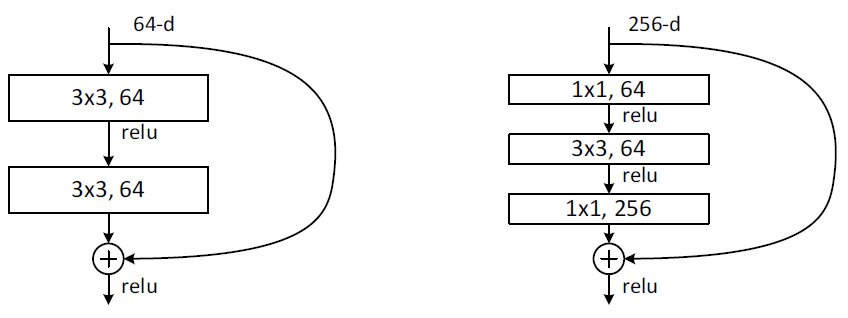
ImageNetで使われた実際のResidual Functionの具体形は以下のようになります。
RNの学習においても最適化にはSGD(+荷重減衰、モーメンタム)が使われています。Adagrad、Adam、RMSPropなどの半自動制御より細やかな手動制御の方がやはり精度向上に寄与するようです。最終的に、ILSVRC2015においては**152層(!)のモデル単体でtop-5エラー率4.49%(この時点で既存のモデル全てを上回る)、異なる深さの6つのモデルのアンサンブルで冒頭のエラー率3.57%**を達成しています。
このモデル自体がRNNの最適化にヒントを得たかどうかは全く定かではありませんが、先行的に行われたRNNの解析によって得られた知見が現在のDNNに還元されている面は否定できないと思われます。
第5部:汎用コンピュータとしてのLSTM
上節で、RNNは真に深いネットワークであるという解釈を紹介しましたが、LSTMの生みの親であるSchmidhuberはさらに突っ込んで、「RNNは汎用コンピュータである」という旨の発言をしています。RNNは可変長の入力を受け取るため、原理的に任意のプログラムを入力することができます。RNNは内部に重み(状態)を持ち、次々に入ってくる入力に応じてその重み(状態)を変化させる、強く解釈すれば自己の状態を変える作業を行っています。これは命令を受けて内部状態(メモリ)を書き換えるノイマン型コンピュータと同じであると考えることができます。Schmidhuberは、RNNはHMM(隠れマルコフモデル)やSVM(Support Vector Machine)が連続的な内部状態を持たないことを根拠に、RNNはそれらのモデルよりも強力で、生物学的に尤もらしいモデルであると主張していますJürgen Schmidhuber's page on Recurrent Neural Networks。
迷路探索などのタスクにRNN(+強化学習)を用いる研究は90年代より為されていましたが、近年は観念的な話に留まらず、実際にRNNやLSTMに命令(Instruction)を解釈・実行させ、汎用性が求められると思われるタスクを解決する取り組みが多数行われています。今回はその中から新しめの事例を1つ紹介します。
誤差逆伝播法&強化学習による簡単なアルゴリズムの学習[Zaremba+ 15]
この論文では、数字列のコピー、複数桁の数字の足し算、数値の掛け算などの簡単なタスクを、入力列の周りを適当に探索して、計算そのものに留まらず計算に至るまでの走査自体も同時に学習するという挑戦的な設定で解くことを目指しています。まずは以下の動画を見ると何をやっているのか何となくわかると思います:
Learning Simple Algorithms from Examples
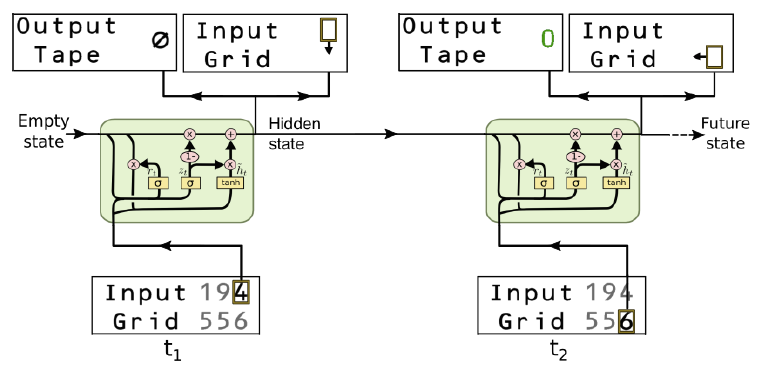
まず、システムはControllerと呼ばれる制御機能を持ったユニットを中心に構成されます。ここにはLSTMや後述のGRU(Gated Recurrent Unit)などのNNが配置されています。今回のタスクは次のような設定でタスクを解くことを要求されます:
まず、入力と出力は
- Input Tape(Grid): 問題で使用する数字列が書かれている1次元の数列または2次元のグリッド
- Output Action: ある場所の数字を受け取った後、グリッド(数列)上のどこに移動するかを判断する
- Output Tape:ある場所の数字を受け取った後、数字またはNOP(Φ)を出力する
の3つから成ります。Controllerは、Input Tapeの現在の値を読み取った後、次のどこのマスに移動するかを判断し、同時に数字またはNOPを出力します。例えば、「ABCDr」(rは終端文字)という文字の反転を行いたければ、ControllerはAの位置にいる状態から計算を開始して、
- Input Tape内の移動:Right Right Right Right Left Left Left Left
- Output Tapeの出力:NOP NOP NOP NOP D C B A
という制御と出力を同時に行う必要があります。本論文ではこれらの制御と出力の学習を誤差逆伝播法と強化学習のアンサンブルで行っています。
- 制御(Action)の学習…出力シンボルが正解であるとき1、不正解であるとき0の報酬を得て強化学習を行う(注:正解は入力列に「埋め込まれている」)
- 出力(Output)の学習…正解と出力シンボルの確率(softmax)とのクロスエントロピー誤差を用いて誤差逆伝播法を行う
このタスクは非常に難しく、例えば3つの数列の足し算などになるとControllerはどこを動き回ればよいのかまったくわかりません。本論文では今日強化学習で広く使われているQ-Learningを改良することで、これらのタスクを**「数列の長さ・問題の複雑さとは関係なく、かつ初見の問題も解けるように」多大なる苦労を以て解決しています(やはり相当苦しかったようで、直接的な正解ではないが、ヒントとなるような知識をQ-Learningの実行時に与えています)。Controllerの部品には200または400個のユニットを持つLSTMが用いられ、LSTMはある特定のアルゴリズムを表すオートマトンを構成するようなメモリ付きのプロセッサ**としての役割を果たしています。これは音声認識などで用いられたときの使い方と似ているようで、その目的は大きく異なっています。
Curriculum Learning
Deep Learningが脚光を浴びた直接のきっかけは「猫の概念を学習した」などでおなじみの画像認識分野でした。しかし、画像認識に比べRNNによる汎用コンピューティングはさらに難しく、教師となるデータを単純に与えただけではうまくいきません。そこで、Curriculum Learning(カリキュラムラーニング)[Bengio+ 09]と呼ばれる簡単な問題から難しい問題を徐々に覚えさせるというアプローチが本論文をはじめ同様のタスクで用いられています。
例えば、3つの数列の足し算であれば、最初のタスクは「1桁の3つの数字の足し算」になります。そして、モデルがうまくそれらの問題を探索・計算できるようになったところで2桁、3桁と徐々に問題の複雑度を上げていきます。しかし、これも一筋縄ではいかず、ある特定の長さの問題に特化してしまうという過学習の特殊形に陥る事例が数多く見られました。
RNNは汎用コンピュータへの道筋となるか?
この論文に留まらず、今現在も多数のRNN(+強化学習)を用いた汎用学習モデルが研究されています。現在はまだ地味に見えますが、数年後に驚くような成果を以て我々の前に現れるかもしれません。しかし間違えてはいけないのは、人間が期待するような様々な問題に対して適切な応答を返す汎用性、あるいは創造性は、適当に多くのデータを与えただけでは達成されないということです。RNN・LSTMを使えば簡単に文章を生成できますが、そのような出力自体には何ら意味はなく、真に汎用的な出力が行われているかどうか慎重な検証が必要となります。
これ以上のCurriculum Learningの詳細については以下を参照してください。
終章:LSTMを超えて
LSTM以外の構造の模索:Gated Recurrent Unit(GRU)[Cho+ 14]
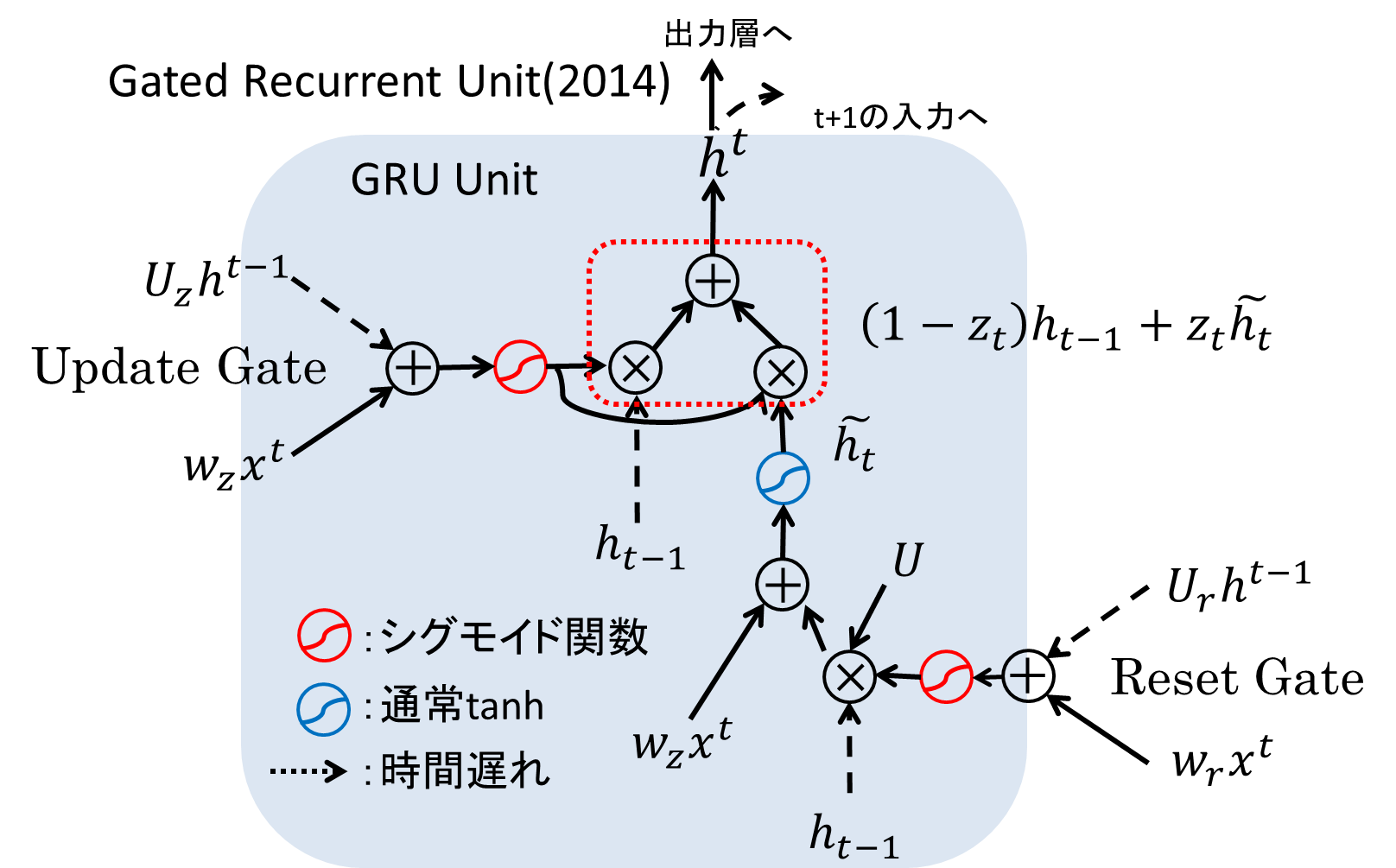
登場から20年が経ち、上で紹介したようにLSTMがどのような性質を持つのか、どのようなタスクに使えるのか、徐々にその性能が見えてくるようになりました。しかし、LSTM以外に同等またはそれ以上の能力を持つ学習器は存在しないのでしょうか?興味深い提案として、ChoらがGated Recurrent Unitと呼ばれるLSTMを簡略化したモデルを提案しています。
GRUの構造は以下の通りです。ゲート数が3つから2つに減って、Update GateとReset Gateの2つのゲートによってメモリセルの中身の維持・出力を制御しています。GRUは機械翻訳のタスクにおいて、LSTMと遜色のない性能を出したことが報告されています。
そこで、[Chung+ 15]においてBengioらのチームはGRUとLSTM、どちらが良いのかどうか判断するべく性能比較を行いました。しかしもどかしいことに、この報告ではLSTMとGRUとの間に明確な優劣をつけることはできなかったとされています。LSTMそのものの解析は進みましたが、LSTMとそれ以外の構造の比較はこれからの課題となりそうです。
LSTMの限界
最後に、LSTMの限界について簡単にコメントしたいと思います。
ここまで紹介してきたとおり、LSTMは勾配消失問題に対応するために発明され、潤沢な計算リソースと合わせて音声認識・機械翻訳などで目覚ましい性能を見出してきました。しかし、LSTMの重大な欠点としてLSTMの構造自体からは、どのような問題が解けるのか・なぜ解けない問題があるのか判断できないことが挙げられます。例えば、Seq-to-Seq Learningによる機械翻訳モデルでは、LSTMが文章の内部表現を獲得していることは示唆されましたが、木構造などによる人間が理解可能な分析は非常に難しくなっています。LSTMを使うときはこの欠点を理解したうえで使う必要があります。
まとめ
- LSTMは時系列データに対する強力な予測モデルである
- Hochreiterの勾配消失問題を解決し、長期の時系列を学習可能になった
- 現在LSTMは単体での使用に留まらず、双方向、複数段の組み合わせによってその表現力を拡大している
- RNNベースで、任意のアルゴリズムを学習させる研究も始まっている
- LSTM以外の有効なアーキテクチャの分析が始まっているが、モデルの構造自体の評価は未だ難しい
- LSTMは強力なモデルだが、やみくもに動かしても意味のある出力を得ることは不可能に近い、緻密な問題設定が必要
LSTMの活躍はまだ始まったばかりです。今後の動きに注目していきましょう。
おわりに
結構頑張って書きました。もう少し洗練させたら印税とか入らないでしょうか。
参考文献
大変多くなったので外部リンクにまとめてあります:
わかるLSTM ~ 最近の動向と共に:参考文献リスト
参考Webページ
LSTM Tutorial
Recurrent Neural Networks(PFIセミナー)
Learning to forget continual prediction with lstm(CV勉強会@関東)
ChainerとRNNと機械翻訳
Curriculum Learning (関東CV勉強会)