はじめに
この記事では、プログラムの計算量を求める方法を説明します。プログラミングの初心者向けに、厳密さよりも分かりやすさを優先して説明していきます。
サンプルコードについて
この記事のサンプルコードは、C言語(C99)で記述しています。
計算量とは?
計算量とは、
「そのプログラムがどれくらい速いかを大雑把に表す指標」
です。
もう少し正確に言うと、
「入力サイズの増加に対して、実行時間がどれくらいの割合で増加するかを表す指標」
です。
グラフによる計算量の表現
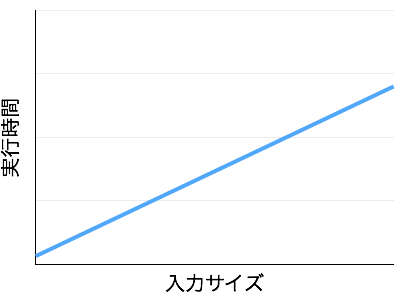
計算量をグラフで表すと、以下のようになります。
これは、**「入力サイズ $n$ が増加するにつれて、実行時間が $n$ に比例して増加する」**ということを表しています。
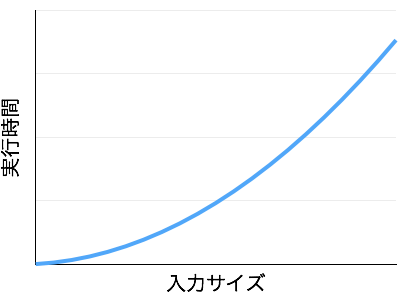
別のグラフも見てみましょう。
これは、**「入力サイズ $n$ が増加するにつれて、実行時間が $n^2$ に比例して増加する」**ということを表しています。
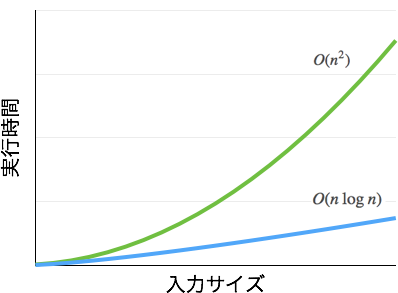
計算量を求めるメリット
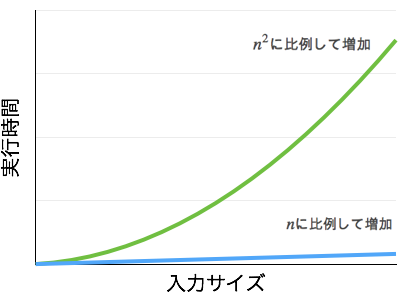
計算量を求めることで2つのアルゴリズムの性能を比較することが可能になります。上記の例で言えば、$n^2$に比例して増加するアルゴリズムより、$n$に比例して増加するアルゴリズムの方が、より性能が良いということがわかります(下図参照)。
O記法による計算量の表現
計算量は一般に、$O$記法(オー記法、もしくはビッグオー記法と呼ぶ)を使って表します。$O$記法では計算量を、$O(n)$ や $O(n^2)$ のような形で記述します。
計算量の求め方
それでは実際に、以下のコードを例に計算量を求めていきましょう。
int calculate(int n) { // nは入力サイズを表す
int count = 0;
for (int i = 0; i < n; i++) {
count++;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
count++;
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
count++;
}
}
return count;
}
計算量は以下の3つの手順で求めます。
手順1)各行のステップ数を求める
はじめに各行のステップ数を以下のように求めます。
int calculate(int n) { // nは入力サイズを表す
int count = 0; // 1回実行
for (int i = 0; i < n; i++) {
count++; // n回実行
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
count++; // n^2回実行
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
count++; // n^2回実行
}
}
return count; // 1回実行
}
手順2)プログラム全体のステップ数を求める
各行のステップ数を足し合わせて、プログラム全体のステップ数を求めます。
\begin{eqnarray}
プログラム全体のステップ数 & = & 1 + n + n^2 + n^2 + 1 \\
& = & 2 + n + 2n^2
\end{eqnarray}
手順3)不要なものを除く
上記の合計ステップ数から不要なものを除きます。
a. 最大次数の項以外を除く
2 + n + 2n^2 \to 2n^2
b. 係数を除く
2n^2 \to n^2
結果
最終的にこのコードの計算量は、
O(n^2)
となります。
計算量を求める際のルール
計算量を求める際には、以下のルールに注意してください。
ルール1)最大次数の項以外を除く
計算量を求める際は、低次項を無視し、最大次数の項だけを残します。例えば、$O(n^2 + n)$ という計算量があった場合、低次項を除いて、$O(n^2)$ とします。
理由)
計算量は、入力サイズが十分に大きいことを前提としてます。そして、入力サイズが大きい場合、低次項の重要性が相対的に低くなるので、これを無視します。
例えば、入力サイズが小さい場合($n = 10$)は、
\begin{eqnarray}
n^2 + n & = & 110 \\
n^2 & = & 100
\end{eqnarray}
となり、低次項の影響が比較的高くなります。しかし、入力サイズが大きい場合($n = 100000$)は、
\begin{eqnarray}
n^2 + n & = & 10000100000 \\
n^2 & = & 10000000000
\end{eqnarray}
となり、入力サイズが大きくなるにつれ、低次項の重要性が低くなっていくことが分かります。
ルール2)係数を除く
また、計算量の定義上、定数倍程度の違いは無視することになっています。例えば、$O(n)$、$O(2n)$、$O(3n)$ は互いに定数倍の違いしかないため、係数部分を無視して、いずれも $O(n)$ として扱います。
注意)計算量による比較は万能ではない
計算量による性能の比較は必ずしも万能ではありません。計算量は、入力サイズが小さい場合や定数倍程度の違いを考慮に入れていません。そのため、計算量の観点から優れているアルゴリズムであっても、現実的にはさほど性能が良くないという場合があります。
実例
順次
- コード
count++; // 1回実行
count++; // 1回実行
- 合計ステップ数
命令が順次に並んでいる場合は、そのステップ数を足しあわせます。上記の場合は、以下のようになります。
合計ステップ数 = 1 + 1 = 2
- 計算量
上記のコードの実行時間は、入力サイズの増減に関わらず一定です。そのような場合、計算量は以下のように書き表します。
O(1)
反復
- コード
for (int i = 0; i < n; i++) { // nは入力サイズとする
count++; // n回実行
}
- 合計ステップ数
n
- 計算量
O(n)
反復(i < n / 3)
- コード
for (int i = 0; i < n / 3; i++) { // nは入力サイズとする
count++; // n/3回実行される
}
- 合計ステップ数
\frac{n}{3}
- 計算量
計算量を求める際は、定数倍程度の違いは無視するので、係数を除きます。
\frac{n}{3} \to O(n)
反復(i += 3)
- コード
for (int i = 0; i < n; i += 3) { // nは入力サイズとする
count++; // n/3回実行される
}
- 合計ステップ数
\frac{n}{3}
補足)
$n = 3$ のとき、$i = 0$ の計1回ループ
$n = 6$ のとき、$i = 0, 3$ の計2回ループ
$n = 9$ のとき、$i = 0, 3, 6$ の計3回ループ
なので、$n/3$ 回ループすることになります。
- 計算量
\frac{n}{3} \to O(n)
反復(i = n / 2)
- コード
for (int i = n / 2; i < n; i++) { // nは入力サイズとする
count++; // n/2回実行される
}
- 合計ステップ数
\frac{n}{2}
補足)
$n = 2$ のとき、$i = 1$ の計1回ループ
$n = 4$ のとき、$i = 2, 3$ の計2回ループ
$n = 6$ のとき、$i = 3, 4, 5$ の計3回ループ
なので、$n/2$ 回ループすることになります。
- 計算量
\frac{n}{2} \to O(n)
反復(i = i * 2)
- コード
for (int i = 1; i <= n; i = i * 2) {
count++; // logn回実行
}
- 合計ステップ数
\log n
- 計算量
O(\log n)
補足)対数の底について
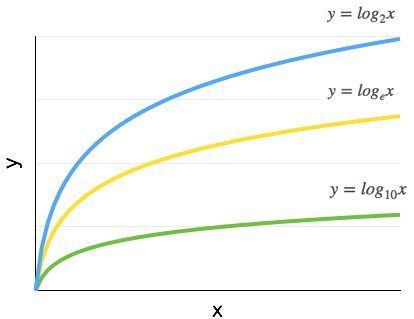
計算量を考える際は、対数の底が何であるかを考える必要はありません。底が $2$、$10$、$e$ のいずれであっても、互いに定数倍の違いしかないためです(下図参照)。計算量を考える際は、定数倍程度の違いは無視します。
補足)ステップ数が logn 回 になる理由
以下に、ステップ数が $\log n$ 回になる理由を説明します。興味がない方は読み飛ばしてください。
先ほどのコードを再掲します。
for (int i = 1; i <= n; i = i * 2) { // nは入力サイズとする
count++; // logn回実行
}
上記のコードのループごとの $i$ の値は以下のようになります。
\begin{eqnarray}
ループ0回目 i & = & 1 & = & 2^0 \\
ループ1回目 i & = & 2 & = & 2^1 \\
ループ2回目 i & = & 4 & = & 2^2 \\
ループ3回目 i & = & 8 & = & 2^3 \\
ループ4回目 i & = & 16 & = & 2^4 \\
\vdots \\
ループk回目 i & = & 2^k
\end{eqnarray}
つまり、$2^k$($k$ はループ回数)が $n$ と等しくなったときにループが終了することになります。
2^k = n
上記の式に対して、両辺の対数をとります。
\log_{2} 2^k = \log_{2} n
公式($\log_{a} y^x = x\log_{a} y$)を適用して、式を変形します。
k\log_{2} 2 = \log_{2} n
$\log_{2} 2 = 1$ なので、
k = \log_{2} n
になります。
計算量を考える際は対数の底を無視してもよいため、最終的には以下のようになります。
k = \log n
つまり、ループ回数($k$)が $\log n$ になることが分かります。
重要)
上記のように、**「繰り返しのたびに問題のサイズが定数分の1になる」場合の計算量は、 $O(\log n)$ になります。例えばバイナリサーチは、「繰り返しのたびに問題のサイズが2分の1になる」**ため、計算量は $O(\log n)$ になります。
反復(i /= 2)
- コード
int i = n; // nは入力サイズとする
while (i > 0) {
i /= 2;
count++; // logn回実行
}
- 合計ステップ数
上記のコードも、繰り返しのたびに問題のサイズが定数分の1になるため、ステップ数は $\log n$ になります。
\log n
- 計算量
O(\log n)
反復(i * i < n)
- コード
for (int i = 0; i * i < n; i++) { // nは入力サイズとする
count++; // sqrt(n)回実行
}
- 合計ステップ数
上記のコードのループは、以下の条件のとき、終了します。
i * i = n
両辺の平方根をとると、以下のようになります。
i = \sqrt{n}
つまり、このコードのステップ数は $\sqrt{n}$ ということになります。
- 計算量
O(\sqrt{n})
反復(i < n * n)
- コード
for (int i = 0; i < n * n; i++) { // nは入力サイズを表す
count++; // n * n回実行
}
- 合計ステップ数
n^2
- 計算量
O(n^2)
反復(入れ子)
- コード
for (int i = 0; i < n; i++) { // n回ループ
for (int j = 0; j < n; j++) { // n回ループ
count++; // n * n回実行
}
}
- 合計ステップ数
for文が入れ子になっている場合は、外側のループと内側のループのループ回数を掛け合わせます。
n^2
- 計算量
O(n^2)
分岐
- コード
if (x > 3) {
for (int i = 0; i < n; i++) { // nは入力サイズを表す
count++; // n回実行
}
} else {
count++; // 1回実行
}
- 合計ステップ数
if文の場合は、より計算量の大きい方に分岐するものとして、ステップ数を求めます。
n
- 計算量
O(n)
別の関数を呼び出す場合
- コード
void doSomething(int n) { // nは入力サイズを表す
for (int i = 0; i < n; i++) { // n回ループ
count++; // n * n回実行
}
}
void calculate(int n) { // nは入力サイズを表す
for (int i = 0; i < n; i++) { // n回ループ
doSomething(n);
}
}
- 合計ステップ数
別の関数を呼び出す場合は、その関数の計算量を考慮に入れるのを忘れないでください。
n^2
- 計算量
O(n^2)
再帰を含む場合
コードに再帰が含まれている場合は、計算量の算出が多少複雑になります。初心者向けの範囲を超えるので、ここでは紹介しません。
参考までに、コードに再帰が含まれている場合は、以下の方法で計算量を求めることになります。
- 漸化式を解く方法
- 公式を利用する方法
一般的によく使われる計算量
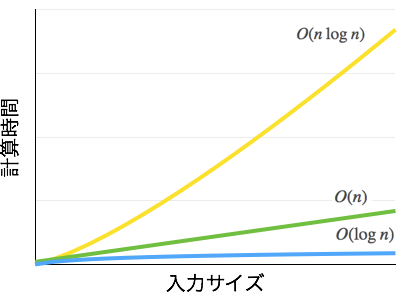
一般的によく使われる計算量の性能比較を以下にまとめます。
性能が良い : O(1) < O(\log n) < O(n) < O(n\log n) < O(n^2) < O(n^3) : 性能が悪い
上記をグラフで表すと、以下のようになります。計算量が大きくなるにつれ、性能が極端に悪くなっていくことが分かります。
補足)ステップ数の求め方について
この記事では、各行のステップ数を求める際に、for文自体のステップ数を無視していました。
for (int i = 0; i < n; i++) { // ここのステップ数をカウントしていない
count++; // n回実行
}
- 合計ステップ数: $n$
- 計算量: $O(n)$
しかし、for文自体のステップ数をカウントしても最終的な結果に違いはありません。
for (int i = 0; i < n; i++) { // n + 1回実行
count++; // n回実行
}
- 合計ステップ数: $n + 1 + n = 2n + 1$
- 計算量: $O(n)$
したがって、計算量を求める際は、どちらのやり方でカウントしてもかまいません。
補足)時間計算量と空間計算量について
計算量には、時間計算量と空間計算量があります。
- 時間計算量 : 実行時間に関する計算量
- 空間計算量 : メモリ使用量に関する計算量
この記事では、時間計算量を取り扱いました。この記事で「計算量」と書いている箇所は、時間計算量のことだと思ってください。