主成分分析(principal component analysis)とは多変量解析手法のうち次元削減手法としてよく用いられる手法の一種で、相関のある多変数から、相関のない少数で全体のばらつきを最もよく表す変数を合成します。
主成分分析を行う便利なツールとして、Pythonで利用可能なScikit-learnなどがありますが、ここではScikit-learnでのPCAの使い方を概観したあと、Scikit-learnを使わずにpandasとnumpyだけでPCAをしてみることで、Pythonの勉強とPCAの勉強を同時に行いたいと思います。
プログラミングにおいて大事なのは「コピペ・タブ補完・ヒストリー機能を極力使うこと」、「一字一句を理解できないと先に進めないのではなく、まずは全部を理解できなくてもいいからゴールまで辿り着き、中身の理解はその後ですること」、「出来上がっているコードの中で、どこを改変すれば自分の目的を達成できるか学ぶこと」、「ときどき変数の中身をチェックすること」などです。頑張ってください。
ワインのデータを例に
データは UC Irvine Machine Learning Repository から取得したものを少し改変しました。
ライブラリのインポート
# 数値計算やデータフレーム操作に関するライブラリをインポートする
import numpy as np
import pandas as pd
# URL によるリソースへのアクセスを提供するライブラリをインポートする。
import urllib.request
# 図やグラフを図示するためのライブラリをインポートする。
import matplotlib.pyplot as plt
%matplotlib inline
import sklearn #機械学習のライブラリ
from sklearn.decomposition import PCA #主成分分析器
データのダウンロード
url = "https://raw.githubusercontent.com/maskot1977/ipython_notebook/master/toydata/wine.txt"
urllib.request.urlretrieve(url, 'wine.txt')
('wine.txt', <http.client.HTTPMessage at 0x11d029198>)
データの読み込みと確認
df = pd.read_csv("wine.txt", sep="\t", index_col=0)
df.head()
| class | Alcohol | Malic acid | Ash | Alcalinity of ash | Magnesium | Total phenols | Flavanoids | Nonflavanoid phenols | Proanthocyanins | Color intensity | Hue | OD280/OD315 of diluted wines | Proline | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 14.23 | 1.71 | 2.43 | 15.6 | 127 | 2.80 | 3.06 | 0.28 | 2.29 | 5.64 | 1.04 | 3.92 | 1065 |
| 1 | 1 | 13.20 | 1.78 | 2.14 | 11.2 | 100 | 2.65 | 2.76 | 0.26 | 1.28 | 4.38 | 1.05 | 3.40 | 1050 |
| 2 | 1 | 13.16 | 2.36 | 2.67 | 18.6 | 101 | 2.80 | 3.24 | 0.30 | 2.81 | 5.68 | 1.03 | 3.17 | 1185 |
| 3 | 1 | 14.37 | 1.95 | 2.50 | 16.8 | 113 | 3.85 | 3.49 | 0.24 | 2.18 | 7.80 | 0.86 | 3.45 | 1480 |
| 4 | 1 | 13.24 | 2.59 | 2.87 | 21.0 | 118 | 2.80 | 2.69 | 0.39 | 1.82 | 4.32 | 1.04 | 2.93 | 735 |
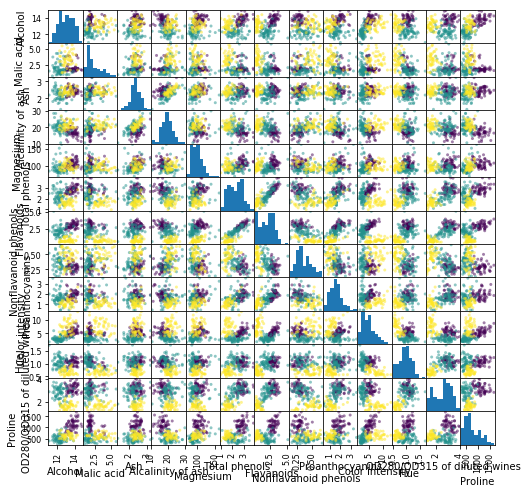
第1列目の「class」というのが品種で、それ以降の列はいろんな観測値です。まずは第1列目以外の散布図行列を作り、第1列目で色分けすることにより、データを概観してみましょう。
from pandas import plotting
plotting.scatter_matrix(df.iloc[:, 1:], figsize=(8, 8), c=list(df.iloc[:, 0]), alpha=0.5)
plt.show()
3品種の特徴がなんとなく分かれていることが見えてきますね。ですが、もっと少ない変数で特徴を説明できないでしょうか。
scikit-learnで主成分分析
行列の標準化
(第1列目以外の)各列に対して、平均値を引いたものを標準偏差で割ります。
# 行列の標準化
dfs = df.iloc[:, 1:].apply(lambda x: (x-x.mean())/x.std(), axis=0)
dfs.head()
| Alcohol | Malic acid | Ash | Alcalinity of ash | Magnesium | Total phenols | Flavanoids | Nonflavanoid phenols | Proanthocyanins | Color intensity | Hue | OD280/OD315 of diluted wines | Proline | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.514341 | -0.560668 | 0.231400 | -1.166303 | 1.908522 | 0.806722 | 1.031908 | -0.657708 | 1.221438 | 0.251009 | 0.361158 | 1.842721 | 1.010159 |
| 1 | 0.245597 | -0.498009 | -0.825667 | -2.483841 | 0.018094 | 0.567048 | 0.731565 | -0.818411 | -0.543189 | -0.292496 | 0.404908 | 1.110317 | 0.962526 |
| 2 | 0.196325 | 0.021172 | 1.106214 | -0.267982 | 0.088110 | 0.806722 | 1.212114 | -0.497005 | 2.129959 | 0.268263 | 0.317409 | 0.786369 | 1.391224 |
| 3 | 1.686791 | -0.345835 | 0.486554 | -0.806975 | 0.928300 | 2.484437 | 1.462399 | -0.979113 | 1.029251 | 1.182732 | -0.426341 | 1.180741 | 2.328007 |
| 4 | 0.294868 | 0.227053 | 1.835226 | 0.450674 | 1.278379 | 0.806722 | 0.661485 | 0.226158 | 0.400275 | -0.318377 | 0.361158 | 0.448336 | -0.037767 |
主成分分析
# 主成分分析の実行
pca = PCA()
pca.fit(dfs)
# データを主成分空間に写像
feature = pca.transform(dfs)
主成分得点
横軸が主成分(PC1, PC2, PC3, ....)、縦軸が各サンプルになります。
# 主成分得点
pd.DataFrame(feature, columns=["PC{}".format(x + 1) for x in range(len(dfs.columns))]).head()
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | PC9 | PC10 | PC11 | PC12 | PC13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3.307421 | -1.439402 | -0.165273 | -0.215025 | 0.691093 | -0.223250 | 0.594749 | 0.064956 | 0.639638 | 1.018084 | -0.450293 | 0.539289 | -0.066052 |
| 1 | 2.203250 | 0.332455 | -2.020757 | -0.290539 | -0.256930 | -0.924512 | 0.053624 | 1.021534 | -0.307978 | 0.159252 | -0.142256 | 0.387146 | 0.003626 |
| 2 | 2.509661 | -1.028251 | 0.980054 | 0.722863 | -0.250327 | 0.547731 | 0.423012 | -0.343248 | -1.174521 | 0.113042 | -0.285866 | 0.000582 | 0.021655 |
| 3 | 3.746497 | -2.748618 | -0.175696 | 0.566386 | -0.310964 | 0.114109 | -0.382259 | 0.641783 | 0.052397 | 0.238739 | 0.757448 | -0.241339 | -0.368444 |
| 4 | 1.006070 | -0.867384 | 2.020987 | -0.408613 | 0.297618 | -0.405376 | 0.442825 | 0.415528 | 0.325900 | -0.078146 | -0.524466 | -0.216055 | -0.079140 |
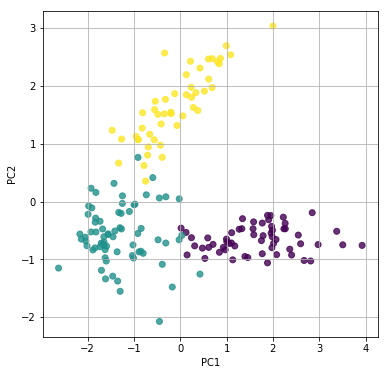
# 第一主成分と第二主成分でプロットする
plt.figure(figsize=(6, 6))
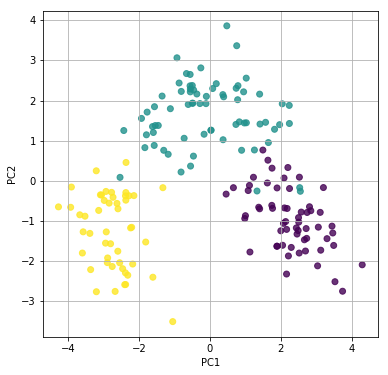
plt.scatter(feature[:, 0], feature[:, 1], alpha=0.8, c=list(df.iloc[:, 0]))
plt.grid()
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.show()
第二主成分(PC2)までで、十分に3品種の区別ができそうです。
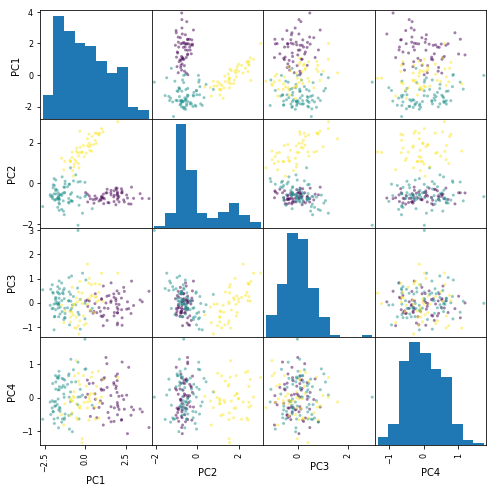
from pandas import plotting
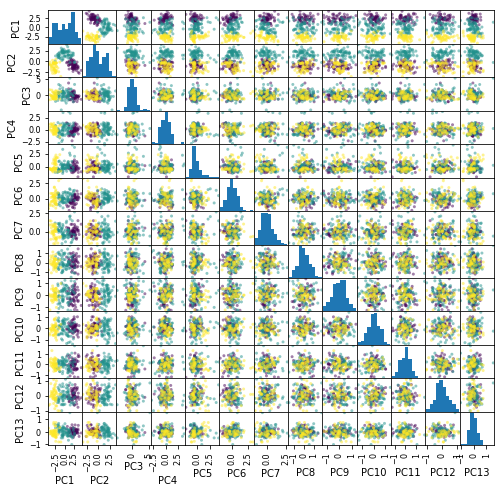
plotting.scatter_matrix(pd.DataFrame(feature,
columns=["PC{}".format(x + 1) for x in range(len(dfs.columns))]),
figsize=(8, 8), c=list(df.iloc[:, 0]), alpha=0.5)
plt.show()
3品種を区別するだけの目的なら、第2主成分までで何とかなりそうです。それ以降の主成分は、意味はあるかもしれませんが、少なくとも3品種を区別するための役には立たなさそうです。
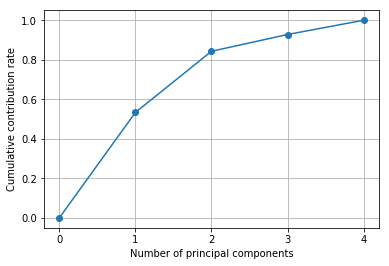
寄与率と累積寄与率
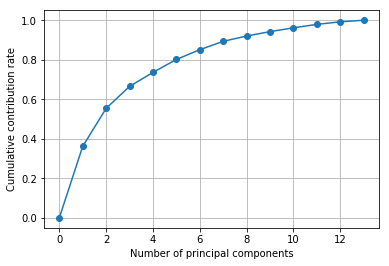
寄与率と累積寄与率は、第何主成分まででどのくらいの情報を説明できるかという指標です。
# 寄与率
pd.DataFrame(pca.explained_variance_ratio_, index=["PC{}".format(x + 1) for x in range(len(dfs.columns))])
| 0 | |
|---|---|
| PC1 | 0.361988 |
| PC2 | 0.192075 |
| PC3 | 0.111236 |
| PC4 | 0.070690 |
| PC5 | 0.065633 |
| PC6 | 0.049358 |
| PC7 | 0.042387 |
| PC8 | 0.026807 |
| PC9 | 0.022222 |
| PC10 | 0.019300 |
| PC11 | 0.017368 |
| PC12 | 0.012982 |
| PC13 | 0.007952 |
# 累積寄与率を図示する
import matplotlib.ticker as ticker
plt.gca().get_xaxis().set_major_locator(ticker.MaxNLocator(integer=True))
plt.plot([0] + list( np.cumsum(pca.explained_variance_ratio_)), "-o")
plt.xlabel("Number of principal components")
plt.ylabel("Cumulative contribution rate")
plt.grid()
plt.show()
固有値と固有ベクトル
各主成分の固有値は以下のとおりになります。
# PCA の固有値
pd.DataFrame(pca.explained_variance_, index=["PC{}".format(x + 1) for x in range(len(dfs.columns))])
| 0 | |
|---|---|
| PC1 | 4.705850 |
| PC2 | 2.496974 |
| PC3 | 1.446072 |
| PC4 | 0.918974 |
| PC5 | 0.853228 |
| PC6 | 0.641657 |
| PC7 | 0.551028 |
| PC8 | 0.348497 |
| PC9 | 0.288880 |
| PC10 | 0.250902 |
| PC11 | 0.225789 |
| PC12 | 0.168770 |
| PC13 | 0.103378 |
各主成分の固有ベクトルは以下のとおりになります。縦軸の数字が主成分になります。
# PCA の固有ベクトル
pd.DataFrame(pca.components_, columns=df.columns[1:], index=["PC{}".format(x + 1) for x in range(len(dfs.columns))])
| Alcohol | Malic acid | Ash | Alcalinity of ash | Magnesium | Total phenols | Flavanoids | Nonflavanoid phenols | Proanthocyanins | Color intensity | Hue | OD280/OD315 of diluted wines | Proline | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PC1 | 0.144329 | -0.245188 | -0.002051 | -0.239320 | 0.141992 | 0.394661 | 0.422934 | -0.298533 | 0.313429 | -0.088617 | 0.296715 | 0.376167 | 0.286752 |
| PC2 | -0.483652 | -0.224931 | -0.316069 | 0.010591 | -0.299634 | -0.065040 | 0.003360 | -0.028779 | -0.039302 | -0.529996 | 0.279235 | 0.164496 | -0.364903 |
| PC3 | -0.207383 | 0.089013 | 0.626224 | 0.612080 | 0.130757 | 0.146179 | 0.150682 | 0.170368 | 0.149454 | -0.137306 | 0.085222 | 0.166005 | -0.126746 |
| PC4 | -0.017856 | 0.536890 | -0.214176 | 0.060859 | -0.351797 | 0.198068 | 0.152295 | -0.203301 | 0.399057 | 0.065926 | -0.427771 | 0.184121 | -0.232071 |
| PC5 | -0.265664 | 0.035214 | -0.143025 | 0.066103 | 0.727049 | -0.149318 | -0.109026 | -0.500703 | 0.136860 | -0.076437 | -0.173615 | -0.101161 | -0.157869 |
| PC6 | -0.213539 | -0.536814 | -0.154475 | 0.100825 | -0.038144 | 0.084122 | 0.018920 | 0.258594 | 0.533795 | 0.418644 | -0.105983 | -0.265851 | -0.119726 |
| PC7 | -0.056396 | 0.420524 | -0.149171 | -0.286969 | 0.322883 | -0.027925 | -0.060685 | 0.595447 | 0.372139 | -0.227712 | 0.232076 | -0.044764 | 0.076805 |
| PC8 | -0.396139 | -0.065827 | 0.170260 | -0.427970 | 0.156361 | 0.405934 | 0.187245 | 0.233285 | -0.368227 | 0.033797 | -0.436624 | 0.078108 | -0.120023 |
| PC9 | 0.508619 | -0.075283 | -0.307694 | 0.200449 | 0.271403 | 0.286035 | 0.049578 | 0.195501 | -0.209145 | 0.056218 | 0.085828 | 0.137227 | -0.575786 |
| PC10 | 0.211605 | -0.309080 | -0.027125 | 0.052799 | 0.067870 | -0.320131 | -0.163151 | 0.215535 | 0.134184 | -0.290775 | -0.522399 | 0.523706 | 0.162116 |
| PC11 | -0.225917 | 0.076486 | -0.498691 | 0.479314 | 0.071289 | 0.304341 | -0.025694 | 0.116896 | -0.237363 | 0.031839 | -0.048212 | 0.046423 | 0.539270 |
| PC12 | -0.266286 | 0.121696 | -0.049622 | -0.055743 | 0.062220 | -0.303882 | -0.042899 | 0.042352 | -0.095553 | 0.604222 | 0.259214 | 0.600959 | -0.079402 |
| PC13 | 0.014970 | 0.025964 | -0.141218 | 0.091683 | 0.056774 | -0.463908 | 0.832257 | 0.114040 | -0.116917 | -0.011993 | -0.089889 | -0.156718 | 0.014447 |
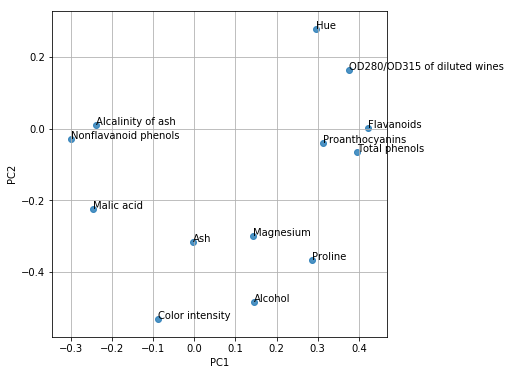
第一主成分と第二主成分における観測変数の寄与度をプロットすることにより、各成分が何を考慮した値なのかのヒントが得られます。
# 第一主成分と第二主成分における観測変数の寄与度をプロットする
plt.figure(figsize=(6, 6))
for x, y, name in zip(pca.components_[0], pca.components_[1], df.columns[1:]):
plt.text(x, y, name)
plt.scatter(pca.components_[0], pca.components_[1], alpha=0.8)
plt.grid()
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.show()
はい、とっても便利ですね。便利すぎて意味分かんないですね。
演習
勉強のために、成分数を減らします。以下の4つの変数だけ考えることにします。
dfs = dfs[['Color intensity', 'Flavanoids', 'Alcohol', 'Proline']]
# 主成分分析を実行してください。
# 第一主成分と第二主成分でプロットしてください。
# PC1〜PC4 で散布図行列を描いてください。
# 寄与率を計算してください。
| 0 | |
|---|---|
| PC1 | 0.533531 |
| PC2 | 0.309520 |
| PC3 | 0.084787 |
| PC4 | 0.072162 |
# 累積寄与率を図示してください。
# 各主成分の固有値を計算してください。
| 0 | |
|---|---|
| PC1 | 2.134122 |
| PC2 | 1.238082 |
| PC3 | 0.339148 |
| PC4 | 0.288648 |
# 各主成分の固有ベクトルを計算してください。
| Color intensity | Flavanoids | Alcohol | Proline | |
|---|---|---|---|---|
| PC1 | 0.409416 | 0.325547 | 0.605601 | 0.599704 |
| PC2 | 0.633932 | -0.725357 | 0.168286 | -0.208967 |
| PC3 | 0.636547 | 0.566896 | -0.388715 | -0.349768 |
| PC4 | -0.159113 | 0.215651 | 0.673667 | -0.688731 |
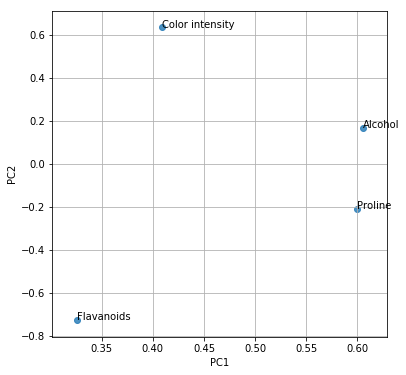
# 第一主成分と第二主成分でプロットする
plt.figure(figsize=(6, 6))
for x, y, name in zip(pca.components_[0], pca.components_[1], ['Color intensity', 'Flavanoids', 'Alcohol', 'Proline']):
plt.text(x, y, name)
plt.scatter(pca.components_[0], pca.components_[1], alpha=0.8)
plt.grid()
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.show()
この固有ベクトルから、ある程度の解釈ができます。
第1主成分は、全ての観測値を正方向に加味した総合指標のようなもの(ワインにとって、全て正であることが良いとは限りませんが)であり、特に「アルコール濃度」「プロリン濃度」に重みを置いた指標になっています。
第2主成分は、「色の濃さ」を正に、「フラボノイド濃度」を負に評価した指標になっています。
このような指標は、ワインの特徴の違いを解釈する助けになるでしょう。
scikit-learnなしで主成分分析
まずは第1主成分(PC1)
相関行列
# 相関行列
dfc = dfs.corr()
dfc
| Color intensity | Flavanoids | Alcohol | Proline | |
|---|---|---|---|---|
| Color intensity | 1.000000 | -0.172379 | 0.546364 | 0.316100 |
| Flavanoids | -0.172379 | 1.000000 | 0.236815 | 0.494193 |
| Alcohol | 0.546364 | 0.236815 | 1.000000 | 0.643720 |
| Proline | 0.316100 | 0.494193 | 0.643720 | 1.000000 |
相関行列の固有値と固有ベクトル
# 固有値と固有ベクトル
eig_val, eig_vec =np.linalg.eig(dfc)
# 固有値
eig_val
array([2.13412212, 1.23808176, 0.33914837, 0.28864774])
# 固有ベクトル
eig_vec
array([[-0.40941602, 0.63393186, -0.63654682, 0.15911338],
[-0.32554699, -0.72535703, -0.56689587, -0.21565114],
[-0.60560142, 0.16828625, 0.38871536, -0.67366685],
[-0.59970376, -0.20896726, 0.34976791, 0.68873107]])
第1主成分の固有ベクトル
# 相関行列の固有ベクトルの第1列を、主成分分析では「第1主成分(PC1)の固有ベクトル」と言います
eig_vec_pc1 = eig_vec[:, 0]
eig_vec_pc1
array([-0.40941602, -0.32554699, -0.60560142, -0.59970376])
# scikit-learn による計算結果と照合してください。正負が逆転することがありますが、気になさらずに。
第1主成分の主成分得点
# 主成分得点(PC1)
pc1 = np.dot(dfs, eig_vec_pc1)
pc1
array([-1.96158489, -0.84437069, -1.45764803, -3.37794671, -0.24091918,
-2.97597478, -2.26455503, -1.98932577, -2.26730282, -1.95585222,
-2.81622301, -1.97061483, -1.98429472, -2.67430795, -3.50890694,
-2.22484682, -2.54821609, -2.06733131, -3.92689454, -0.99735336,
-1.3296379 , -0.01685181, -1.13293227, -0.31004679, -0.47699845,
-0.14615498, -1.39507959, -1.10478452, -1.17671713, -1.34387136,
-2.08008249, -2.59856235, -0.96999543, -1.78804312, -1.05456986,
-1.00453015, -0.59308299, -0.70670392, -0.53106241, -1.27140504,
-1.10909632, -0.9287257 , -1.88349832, -0.12368722, -0.61303024,
-1.77096318, -1.97864591, -1.75185362, -1.90835535, -2.84877329,
-1.58715156, -2.01419305, -2.36441818, -2.23735474, -1.57147534,
-1.58299377, -1.88433998, -1.76975075, -2.40377192, 1.9270171 ,
1.24956142, 0.91404783, 0.0234326 , 0.85137293, 1.82924743,
0.48021577, -0.03299298, 0.99787085, 0.31203842, 1.27896044,
0.97923499, 0.02610127, 0.45290031, -0.42439989, 0.80165057,
1.97922727, 0.73459567, 1.99240963, 0.84559797, 1.03458206,
2.01595296, 0.3132995 , 1.56053876, 0.59352112, 1.59361297,
1.27169865, 1.67795044, 1.9303867 , 1.65173541, 1.64803881,
1.83694882, 1.82331441, 1.25158389, 1.84183816, 2.03937735,
0.38943876, 1.91078494, 1.36510168, 0.17364405, 1.35325951,
1.0216329 , 1.32968167, 1.45352786, 2.16910312, 0.91828738,
1.73374721, 1.30366187, 1.10060892, 1.82347134, 1.29972473,
1.70299948, 1.62358288, 1.41382298, 2.13804421, 1.67208756,
2.62917697, 2.04921573, 1.7081619 , 1.43277679, 1.88882534,
1.46022922, 0.4508606 , 1.65350546, 0.89366481, 1.61474424,
1.60027154, 1.00988393, 1.73280081, 1.62324673, 1.55954937,
0.75068685, 0.70639925, 0.69087459, 0.78452743, 0.95364189,
0.48333879, 1.33270418, 1.26876675, 0.34433528, 0.90881451,
0.91173787, 0.07157763, 0.66159608, 0.4297798 , 0.20458922,
0.39182207, 0.55453927, 0.32136008, -0.23377302, -0.242701 ,
-0.37817409, -0.1305284 , 0.41500516, -0.60792532, 0.54077128,
-0.13050252, -0.42494476, 0.19835677, -2.00180696, -0.99489754,
0.81376864, -0.05315963, 0.82288447, 0.56125632, -0.68905354,
0.12034891, -0.86771637, -0.21979684, -0.68662254, -0.33467534,
1.47200968, 0.3394088 , -1.0859315 , -0.52005519, -0.28283458,
-0.84032362, -0.61304633, -0.80436788])
# scikit-learn による計算結果と照合してください。正負が逆転することがありますが、気になさらずに。
第1主成分の固有値
# 相関行列の固有値の第1成分を、主成分分析では「第1主成分(PC1)の固有値」と言います
eig_val_pc1 = eig_val[0]
eig_val_pc1
2.1341221243556294
# scikit-learn による計算結果と照合してください。
次に第2主成分 (PC2)
- PC1の影響を取り除いた相関行列2
# 相関行列から、PC1の影響を取り除いた相関行列2を作成します
matrix = []
for d1 in eig_vec_pc1:
mat = []
for d2 in eig_vec_pc1:
mat.append(d1 * d2)
matrix.append(mat)
matrix = np.array(matrix)
dfc2 = dfc - matrix * eig_val_pc1
dfc2
| Color intensity | Flavanoids | Alcohol | Proline | |
|---|---|---|---|---|
| Color intensity | 0.642275 | -0.456824 | 0.017224 | -0.207887 |
| Flavanoids | -0.456824 | 0.773824 | -0.183931 | 0.077545 |
| Alcohol | 0.017224 | -0.183931 | 0.217304 | -0.131354 |
| Proline | -0.207887 | 0.077545 | -0.131354 | 0.232474 |
- PC1の影響を取り除いた相関行列2の固有値と固有ベクトル
# 固有値と固有ベクトル を求めてください。
- 第2主成分(PC2)の固有ベクトル
# 相関行列2の固有ベクトルの第1列を、主成分分析では「第2主成分(PC2)の固有ベクトル」と言います。
# 第2主成分(PC2)の固有ベクトルを求め、scikit-learn による計算結果と照合してください。
- 第2主成分(PC2)の主成分得点
# 主成分得点(PC2)を求め、scikit-learn による計算結果と照合してください。
- 第2主成分(PC2)の固有値
# 相関行列2の固有値の第1成分を、主成分分析では「第2主成分(PC2)の固有値」と言います
# 第2主成分(PC2)の固有値を求め、scikit-learn による計算結果と照合してください。
続いて第3主成分 (PC3)
- PC2の影響を取り除いた相関行列3
# 相関行列2から、PC2の影響を取り除いた相関行列3を作成してください。
| Color intensity | Flavanoids | Alcohol | Proline | |
|---|---|---|---|---|
| Color intensity | 0.144728 | 0.112479 | -0.114857 | -0.043877 |
| Flavanoids | 0.112479 | 0.122416 | -0.032801 | -0.110119 |
| Alcohol | -0.114857 | -0.032801 | 0.182241 | -0.087815 |
| Proline | -0.043877 | -0.110119 | -0.087815 | 0.178411 |
- PC2の影響を取り除いた相関行列3の固有値と固有ベクトル
# 固有値と固有ベクトルを求めてください。
- 第3主成分(PC3)の固有ベクトル
# 相関行列3の固有ベクトルの第1列を、主成分分析では「第3主成分(PC3)の固有ベクトル」と言います
# 第3主成分(PC3)の固有ベクトルを求め、scikit-learn による計算結果と照合してください。
- 第3主成分(PC3)の主成分得点
# 主成分得点(PC3)を求め、scikit-learn による計算結果と照合してください。
- 第3主成分(PC3)の固有値
# 相関行列3の固有値の第1成分を、主成分分析では「第3主成分(PC3)の固有値」と言います
# 第3主成分(PC3)の固有値を求め、scikit-learn による計算結果と照合してください。
最後に第4主成分(PC4)
- PC3の影響を取り除いた相関行列4
# 相関行列2から、PC2の影響を取り除いた相関行列3を作成してください。
| Color intensity | Flavanoids | Alcohol | Proline | |
|---|---|---|---|---|
| Color intensity | 0.007308 | -0.009904 | -0.030940 | 0.031632 |
| Flavanoids | -0.009904 | 0.013424 | 0.041934 | -0.042872 |
| Alcohol | -0.030940 | 0.041934 | 0.130996 | -0.133925 |
| Proline | 0.031632 | -0.042872 | -0.133925 | 0.136920 |
- PC3の影響を取り除いた相関行列4の固有値と固有ベクトル
# 固有値と固有ベクトルを求めてください。
- 第4主成分(PC4)の固有ベクトル
# 相関行列4の固有ベクトルの第1列を、主成分分析では「第4主成分(PC4)の固有ベクトル」と言います
# 第4主成分(PC4)の固有ベクトルを求め、scikit-learn による計算結果と照合してください。
- 第4主成分(PC4)の主成分得点
# 主成分得点(PC4)を求め、scikit-learn による計算結果と照合してください。
- 第4主成分(PC4)の固有値
# 相関行列4の固有値の第1成分を、主成分分析では「第4主成分(PC4)の固有値」と言います
# 第4主成分(PC4)の固有値を求め、scikit-learn による計算結果と照合してください。
寄与率
各主成分の固有値を足し合わせて割合をとったものを「寄与率」といいます。
eig_val_pca = np.array([eig_val_pc1, eig_val_pc2, eig_val_pc3, eig_val_pc4])
eig_val_pca
array([2.13412212, 1.23808176, 0.33914837, 0.28864774])
eig_val_pca / eig_val_pca.sum()
array([0.53353053, 0.30952044, 0.08478709, 0.07216194])
# scikit-learn による計算結果と照合してください。
課題
-
同じデータに対して Alcohol, Flavanoids, Nonflavanoid phenols, Proanthocyanins, Color intensity, Hue の6変数を使って主成分分析し、その結果について考察してください。scikit-learnを使って構いません。
-
実習用データ にある 「都道府県別アルコール類の消費量」 のデータを主成分分析し、その結果の解釈をしてください。scikit-learnを使って構いません。