Go to Qiita Advent Calendar 2024 Top
LoginSignup
297
259

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@Rijicho_nl(りじちょー)

UX最強のベジェ曲線「κ-Curves」を完全に理解する

Last updated at Posted at 2020-02-04

#TL;DR

  • 全てのユーザ制御点上を通り、
  • 全ての曲率極大点がユーザ制御点上にある

そんな超便利なのにあまり知られていないパラメトリック曲線こと**「κ-Curves」**。
Adobe ResearchとテキサスA&M大学のYan氏らがSIGGRAPH 2017で発表した研究で、Adobe Illustratorに実装されており、Adobeが特許を取っています（無断の商用利用はNG）。
新しめなせいか、検索しても情報があまり出てきません。
この論文と同じ流れを、前提知識や行間を補いつつ日本語で追っていきます。

C#で実際に実装もしていきます。
論文に忠実に実装するとちょっとバグるので、それについても少し。

※本記事では、上記論文から一部画像や式を引用しています。

image.png
これは論文から引用した図で、他の様々なパラメトリック曲線とκ-Curvesの比較。
左から順に、Interpolatory subdivision curve, Catmull-Romスプライン、Cubic B-スプライン、κ-Curvesです。

#デモ
WebGL(JavaScript)で実装したものをGlitchに公開しました。

注意：

#事前知識
簡単のため、本記事ではxy平面上の曲線のみを考えます。
高校レベルの数学＋行列の基礎知識で理解できる内容のはずです。

##パラメトリック曲線

パラメトリック曲線とは、X座標、Y座標がそれぞれパラメータ$t$によって決まる曲線です。

\begin{align}
&f:\mathbb{R}\rightarrow\mathbb{R}^2\\
&f(t)=
\left(\begin{matrix}
x(t)\\
y(t)
\end{matrix}\right)
\end{align}

世の中には様々なパラメトリック曲線があります。いくつか雑に紹介すると、

  • （３次）エルミート曲線
    • $f(0), f(1), f'(0),f'(1)$の値が制約として与えられ、それを満たすような$t$の３次式。
    • あんまり融通が効かない。
  • （n次）ベジェ曲線
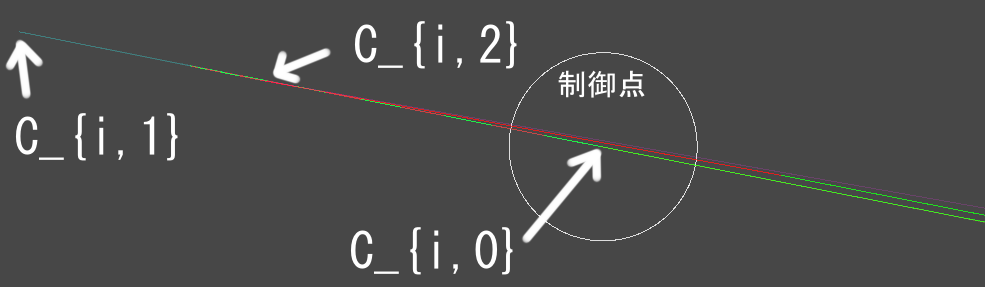
    • 連続する各セグメント$i$について、制御点$c_{i,0}, \cdots, c_{i,n}$が与えられる。
    • $c_{i,0}, c_{i,n}$を結ぶ線をそれ以外の制御点がそれぞれ引っ張ったような曲線になる。
    • 曲線は$c_{i,0}, c_{i,n}$以外の制御点の上を通らない。
  • スプライン曲線
    • ３次曲線などをいくつも繋げたり重ねたりして一本の曲線を作るもの。
    • いろいろと種類がある。Catmull-Romスプライン、B-スプライン、NURBSなど。
    • 接続点を制御点として動かすタイプの場合、曲線は制御点上を通る。
      • が、通るだけで、期待した形になるとは限らない。
      • なんかひん曲がってしまう例（Excelの曲線ツール）：image.png

と、他にもいろいろありますが、とにかくどれもこれも融通が効きません。
イラストソフトなどでポチポチクリックした場所をいい感じになめらかに繋いで曲線を作ってほしい場合、どれも力不足。

κ-Curvesは、曲率を制御することでこれを実現します。
※ベースはベジェ曲線なので、ベジェ曲線以外のことは忘れて大丈夫です。

##曲率
κ-Curvesは、「ユーザー制御点の曲率の絶対値が極大になる」という特徴を持つ曲線です。
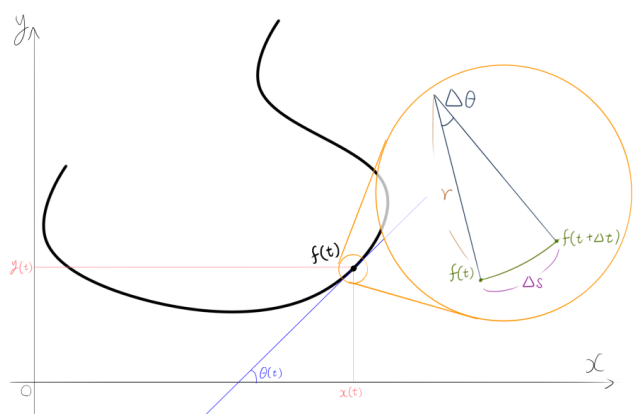
曲率（Curvature）とは、曲線上のある点の周りの微小区間を円弧に近似したときの円の半径の逆数（符号付き1）です。
要は、曲線上のある点の周囲がいかに急カーブかを示す値ですね。絶対値が大きいほど急になります。

具体的には、2Dパラメトリック曲線においては以下の式で表される値です。

\kappa(t)=\frac{f'(t)\times f''(t)}{\|f'(t)\|^3}

軽く導出しておきましょう。
image.png

平面曲線$f:\mathbb{R}\rightarrow\mathbb{R}^2$において、ある微小区間$f(t)$～$f(t+\Delta t)$の長さを$\Delta s$、それが円弧だとしたときの中心角を$\Delta\theta$、半径を$r$とすると、$\Delta s=r\Delta\theta$が成り立ちます。これより、点$f(t)$における曲率$\kappa(t)$は、

\kappa(t)=\lim_{\Delta t\rightarrow0}\frac{\Delta \theta}{\Delta s}=\frac{d\theta}{ds}

と表されます。

ここで、$\dot{x}=\frac{dx}{dt},\ \dot{y}=\frac{dy}{dt}$とすると、点$f(t)$における傾きは

\tan\theta=\frac{dy}{dx}=\frac{\dot{y}}{\dot{x}}

ですが、この両辺を$t$で微分すると、

\begin{align}
\frac{1}{\cos^2\theta}\frac{d\theta}{dt}&=\frac{\dot{x}\ddot{y}-\dot{y}\ddot{x}}{\dot{x}^2}\\\\
\frac{d\theta}{dt}&=\frac{1}{1+\tan^2\theta}\frac{\dot{x}\ddot{y}-\dot{y}\ddot{x}}{\dot{x}^2}\\\\
\frac{d\theta}{dt}&=\frac{\dot{x}\ddot{y}-\dot{y}\ddot{x}}{\dot{x}^2 + \dot{y}^2}
\end{align}

が得られます。ドット２つは$t$での二階微分です。
また、$\Delta s$は微小区間の長さなので、

\frac{ds}{dt}=\sqrt{\dot{x}^2+\dot{y}^2}

であり、以上から

\begin{align}
\kappa(t)&=\frac{d\theta}{ds}=\frac{\dot{x}\ddot{y}-\dot{y}\ddot{x}}{(\dot{x}^2 + \dot{y}^2)^{\frac{3}{2}}}\\\\
&=\frac{f'(t)\times f''(t)}{\|f'(t)\|^3}
\end{align}

が導かれます。

κ-Curvesは、ユーザ制御点上でこの値（の絶対値）が極大値を取るような曲線である、ということです。

ベジェ曲線

先程少し触れましたが、κ-Curvesはベジェ曲線がベースになっています。
というか、曲線の式自体はベジェ曲線そのものなのです。
というわけで、まずはベジェ曲線について。

表式

いくつものベジェ曲線を連結して一本の曲線にすることを考えます。
この各ベジェ曲線をセグメントと呼ぶことにし、それぞれの$t$の変域を$[0,1]$とします。

一般の$d$次ベジェ曲線の$i$番目のセグメントは、$c_{i,j}$をそのセグメントのベジェ制御点とすると

c_i^d(t)=\sum_{j=0}^d\frac{d!}{(d-j)!j!}(1-t)^{d-j}t^jc_{i,j}

で表されますが、κ-Curvesにおいては次に示す2次ベジェ曲線を前提とします。$d$のことは忘れてください。

\begin{align}
c_i(t)&=(1-t)^2c_{i,0} + 2(1-t)tc_{i,1} + t^2c_{i,2}\\
&=(c_{i,0}-2c_{i,1}+c_{i,2})t^2-2(c_{i,0}-c_{i,1})t+c_{i,0}\\
\end{align}

二階微分まで求めておくと、

\begin{align}
c_i'(t)&=2(c_{i,0}-2c_{i,1}+c_{i,2})t-2(c_{i,0}-c_{i,1})\\
&=2((1-t)(c_{i,1}-c_{i,0})+t(c_{i,2}-c_{i,1}))\\
\\
c_i''(t)&=2(c_{i,0}-2c_{i,1}+c_{i,2})\\
&=2((c_{i,0}-c_{i,1}) + (c_{i,2} - c_{i,1}))
\end{align}

となります。

###曲率

$i番目の$セグメントの各点$c_i(t)$における曲率を$\kappa_i(t)$とすると、

\begin{align}
\kappa_i(t)&=\frac{c_i'(t)\times c_i''(t)}{\|c_i'(t)\|^3}\\
&=\frac{\triangle(c_{i,0},c_{i,1},c_{i,2})}{\|(1-t)(c_{i,1}-c_{i,0})+t(c_{i,2}-c_{i,1})\|^3}\\
\end{align}\\

となります。ここで$\triangle(c_{i,0},c_{i,1},c_{i,2})$は３つの制御点を結んだ三角形の符号付き面積で、つまり定数です。

……何ともよく分からん式変形なので、図解します。
同じ色の線分は平行です。
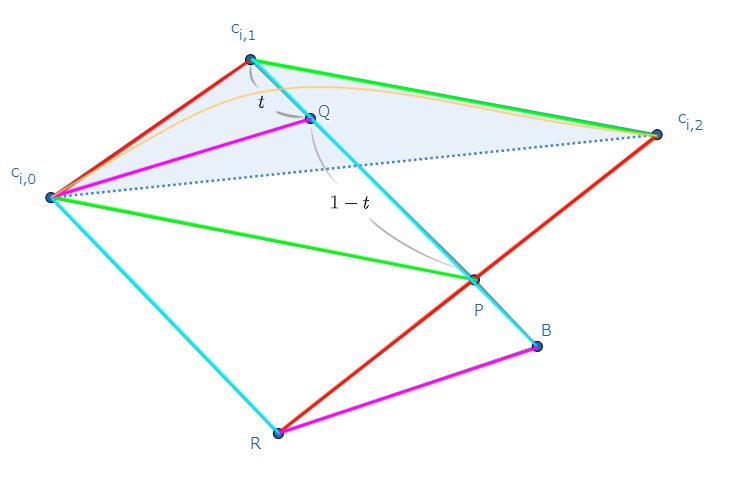
k0.png
$c_{i,0},c_{i,1},c_{i,2}$を３点とする平行四辺形の残りの点（$c_{i,1}$の対角位置）を$P$とし、
$c_{i,0},c_{i,1},P$を３点とする平行四辺形の残りの点（$c_{i,1}$の対角位置）を$R$とします。

$c_{i,0}$を原点としたときに、$\frac{1}{2}c_i'(t)=(1-t)(c_{i,1}-c_{i,0})+t(c_{i,2}-c_{i,1})$がどこを示す位置ベクトルになるかというと、見たまんま内分点なので図の点$Q$です。

同じように、$\frac{1}{2}c_i''(t)=(c_{i,0}-c_{i,1}) + (c_{i,2} - c_{i,1})$は点$R$を示します。

よって、これらの外積$\frac{1}{4}c_i'(t)\times c_i''(t)$の絶対値は、以下の領域の面積になります。
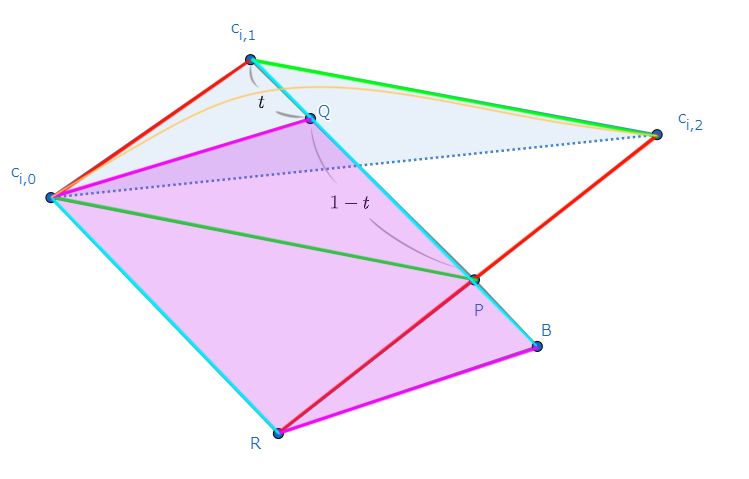
k1.png
これは、以下の領域の面積と等しいことが等積変形によってわかります。
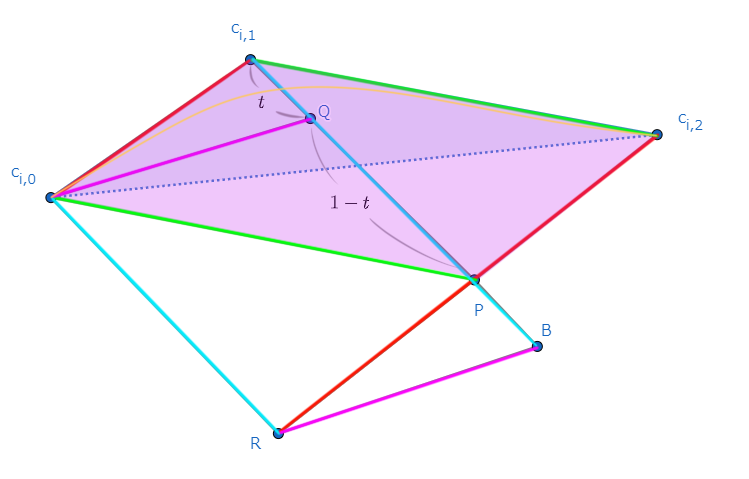
k2.png
よって、$t$の値によらず、

\frac{1}{4}c_i'(t)\times c_i''(t)=2\triangle(c_{i,0},c_{i,1},c_{i,2})

であることが分かります。初等幾何は楽しいですね。

というわけで再掲すると、２次ベジェ曲線の$i$番目のセグメント上の点$c_i(t)$における曲率は、

\kappa_i(t)=\frac{\triangle(c_{i,0},c_{i,1},c_{i,2})}{\|(1-t)(c_{i,1}-c_{i,0})+t(c_{i,2}-c_{i,1})\|^3}

で求められます。

※面積の符号については、最終的に絶対値で吸収されるのであまり気にしなくて大丈夫です。

曲率極大点

曲率の絶対値が極大になるときの$t$を$t_i$とすると、$\kappa'(t_i)=0$より、

\begin{align}
\kappa'(t_i)=-\frac{\triangle(c_{i,0},c_{i,1},c_{i,2})\cdot 3(\|c_i'(t_i)\|)'}{\|c_i'(t_i)\|^4}&=0\\\\
(\|c_i'(t_i)\|)'&=0\\\\
c_i'(t_i)c_i''(t_i)&=0\\\\
((c_{i,0}-2c_{i,1}+c_{i,2})t_i-(c_{i,0}-c_{i,1}))\cdot(c_{i,0}-2c_{i,1}+c_{i,2})&=0
\end{align}

というわけで

t_i=\frac{(c_{i,0}-c_{i,1})\cdot(c_{i,0}-2c_{i,1}+c_{i,2})}{\|c_{i,0}-2c_{i,1}+c_{i,2}\|^2}

となります。
$c_{i,1}$から見たローカル座標として、$c_{i,0}'=c_{i,0}-c_{i,1},\ c_{i,2}'=c_{i,2}-c_{i,1}$とおけば、

t_i=\frac{c_{i,0}'\cdot(c_{i,0}'+c_{i,2}')}{\|c_{i,0}'+c_{i,2}'\|^2}

とそこそこ綺麗な形になります。

このように、与えられたベジェ制御点から曲率極大点を求めるのは簡単です。
κ-Curvesはこの逆、与えられたユーザ制御点を曲率極大点$c_i(t_i)$とし、それを満たすベジェ制御点を逆算するシステムです。

κ-Curves

いよいよκ-Curvesを構成していきます。
問題の大枠は以下の通り：

入力：$n$個のユーザ制御点$p_i\ (0\le i<n)$
出力：$3n$個のベジェ制御点$c_{i,j}\ (0\le i<n,\ j=0,1,2)$

制約１：ユーザ制御点で極大曲率
制約２：$C^0$連続
制約３：$G^1$連続
制約４：ほぼ$G^2$連続

４つの制約を順に見ていきましょう。

※ベジェ制御点$c_{i,j}$の添字$i$については、ひとまずはループしているものとみなし、$\rm{mod}\ n$で考えます。
　範囲制限をつけずに$i+1$とか$i-1$とか書きますが怒らないでください。非ループ版への拡張は簡単です。

##制約１：ユーザ制御点で極大曲率
$p_i=c_i(t_i)$を、$c_{i,1}$について整理してみます。

\begin{align}
p_i&=c_i(t_i)\\
p_i&=(c_{i,0}-2c_{i,1}+c_{i,2})t_i^2-2(c_{i,0}-c_{i,1})t_i+c_{i,0}\\\\
c_{i,1}&=\frac{p_i-(1-t_i)^2c_{i,0}-t^2c_{i,2}}{2t_i(1-t_i)}
\end{align}

※$t_i=0, 1$のときはそれぞれ$p_i=c_{i,0}, c_{i,2}$のときなので、個別に簡単に考えることができます。
これを先程導出した$t_i$の式：

t_i=\frac{(c_{i,0}-c_{i,1})\cdot(c_{i,0}-2c_{i,1}+c_{i,2})}{\|c_{i,0}-2c_{i,1}+c_{i,2}\|^2}

に代入して気合で整理すると、以下の$t_i$の三次方程式が得られます。

\|c_{i,2}-c_{i,0}\|^2t_i^3+3(c_{i,2}-c_{i,0})\cdot(c_{i,0}-p_i)t_i^2+(3c_{i,0}-2p_i-c_{i,2})\cdot(c_{i,0}-p_i)t_i-\|c_{i,0}-p_i\|^2=0

ただの３次方程式なので、解の公式（カルダノの公式）で解くことができます。
係数がごちゃごちゃしていますが、$c_{i,0}$から見たローカル座標で $c_{i,2}'=c_{i,2}-c_{i,0},\ p_i'=p_i-c_{i,0}$ と書き直せば、少し短くなります。

\|c'_{i,2}\|^2t_i^3-3c'_{i,2}p'_it_i^2+(2p_i'+c_{i,2}')p_i't_i-\|p_i'\|^2=0

綺麗にする

もっと綺麗に整理するために、$p_i$から見たローカル座標で考えてみましょう。
$v_0=c_{i,0}-p_i,\ v_2=c_{i,2}-p_i$とすると、

\|v_2-v_0\|^2t_i^3+3(v_2-v_0)v_0t_i^2+(3v_0-v_2)v_0t_i-\|v_0\|^2=0

ですが、これは以下のように変形できます。

\left(\begin{matrix}
\|v_0\|^2\\
v_0\cdot v_2\\
-v_0\cdot v_2\\
-\|v_2\|^2
\end{matrix}\right)
\cdot
\left(\begin{matrix}
(1-t_i)^3\\
t_i(1-t_i)^2\\
t_i^2(1-t_i)\\
t_i^3
\end{matrix}\right)
=0

対称的な形になりました。
２つ目、３つ目の係数を調整すれば３次のバーンスタイン多項式として扱えます。

実解の範囲と個数

ところでこの方程式は、必ず$[0,1]$内にただ１つの実解を持ちます。
さすがに自明ではなく、論文にもAppendixに証明があります。概略は以下のとおり：

  1. まず中間値の定理より、$[0,1]$内に実解が一つ以上存在します。
  2. デカルトの符号律はバーンスタイン多項式にも適用できる（らしい）ので、$v_0\cdot v_2\ge 0$であれば実解は１つだけです。
  3. $v_0\cdot v_2<0$の場合も、導関数の正負は$[0,1]$内で一定であることが示せるので、実解は１つだけです。

制約２：C⁰連続

曲線全体の位置が連続であることを保証する制約です。
各セグメント内が連続なのは自明として、隣り合うセグメントが端点で互いに接続していればよいので、
任意の$i$について、

c_{i,2}=c_{i+1,0}

が満たされればよいですね。簡単。次に行きましょう。

制約３：G¹連続

セグメントの接続点の傾きが連続であることを保証する制約です。
これがないと、セグメントとセグメントの間で線が折れてしまいます。

任意の$i$について、ある$\lambda_i\in(0,1)$があって、

c_{i,2}=(1-\lambda_i)c_{i,1}+\lambda_ic_{i+1,1}

が満たされれば、$c_{i,2}=c_{i+1,0}$における接線は$c_{i,1}$と$c_{i+1,1}$を結ぶ直線に定まります。
κ-Curvesにおいてベジェ制御点は入力ではなく出力なので、これで全ての場合が網羅されています。

ユーザ制御点位置の別表示

またこの制約のもとでは、ユーザ制御点の位置$p_i=c_i(t_i)$を、$c_{i,0}, c_{i,2}$を使わずに以下のように表現可能です。

p_i=(1-\lambda_{i-1})(1-t_i)^2c_{i-1,1}+\big(\lambda_{i-1}(1-t_i)^2+(2-(1+\lambda_i)t_i)t_i\big)c_{i,1}+\lambda_it_i^2c_{i+1,1}

何でそんな変形を？　と思うかもしれませんが、後で使います。

制約４：ほぼG²連続

セグメントの接続点の曲率が（ほぼ）連続であることを保証する制約です。

\kappa_i(t)=\frac{\triangle(c_{i,0},c_{i,1},c_{i,2})}{\|(1-t)(c_{i,1}-c_{i,0})+t(c_{i,2}-c_{i,1})\|^3}

で、任意の$i$について$\kappa_i(1)=\kappa_{i+1}(0)$であればいいので、

\begin{align}
\kappa_i(1)&=\kappa_{i+1}(0)\\\\
\frac{\triangle(c_{i,0},c_{i,1},c_{i,2})}{\|c_{i,2}-c_{i,1}\|^3}
&=\frac{\triangle(c_{i+1,0},c_{i+1,1},c_{i+1,2})}{\|c_{i+1,1}-c_{i+1,0}\|^3}\\\\
\frac{\triangle(c_{i,0},c_{i,1},c_{i,2})}{\|c_{i,1}-c_{i+1,1}\|^3\lambda_i^3}
&=\frac{\triangle(c_{i+1,0},c_{i+1,1},c_{i+1,2})}{\|c_{i,1}-c_{i+1,1}\|^3(1-\lambda_i)^3}\\\\
\frac{\triangle(c_{i,0},c_{i,1},c_{i+1,1})}{\lambda_i^2}
&=\frac{\triangle(c_{i,1},c_{i+1,1},c_{i+1,2})}{(1-\lambda_i)^2}
\end{align}

より（最後の式変形は図を書いて面積比に着目するとすぐ分かります）、

\lambda_i=\frac{\sqrt{\triangle(c_{i,0},c_{i,1},c_{i+1,1})}}{\sqrt{\triangle(c_{i,0},c_{i,1},c_{i+1,1})}+\sqrt{\triangle(c_{i,1},c_{i+1,1},c_{i+1,2})}}

が得られます。

ところで、ベジェ曲線の曲率が０になることはないので、隣り合うセグメントの凹凸が逆である場合、曲率は必ず不連続になります。
このとき、$\triangle(c_{i,0},c_{i,1},c_{i+1,1}),\triangle(c_{i,1},c_{i+1,1},c_{i+1,2})$の符号が異なるので、$\lambda_i$は実数ではなくなります。

一致させられないのであれば、せめて絶対値の差を０にしましょう。
つまり$|\kappa_i(1)|=|\kappa_{i+1}(0)|$を解くわけですが、$\kappa_i(1)$と$\kappa_{i+1}(0)$の符号は逆なので、$\kappa_i(1)=-\kappa_{i+1}(0)$を解けばいいことがわかります。
すると、曲率が連続の場合とほぼ同様の手順で、以下が求まります。

\lambda_i=\frac{\sqrt{|\triangle(c_{i,0},c_{i,1},c_{i+1,1})|}}{\sqrt{|\triangle(c_{i,0},c_{i,1},c_{i+1,1})|}+\sqrt{|\triangle(c_{i,1},c_{i+1,1},c_{i+1,2})|}}

これは先程の式も包含できているので、制約式としてはこちらのみを使えばよさそうです。

制約まとめ

制約とその関連式をまとめると、

\left\{\begin{array}{ll}
(1)&\|c'_{i,2}\|^2t_i^3-3c'_{i,2}p'_it_i^2+(2p_i'+c_{i,2}')p_i't_i-\|p_i'\|^2=0\\
&(c_{i,2}'=c_{i,2}-c_{i,0},\ p_i'=p_i-c_{i,0})\\\\
(2)&c_{i,2}=c_{i+1,0}=(1-\lambda_i)c_{i,1}+\lambda_ic_{i+1,1}\\\\
(3)&p_i=(1-\lambda_{i-1})(1-t_i)^2c_{i-1,1}+\big(\lambda_{i-1}(1-t_i)^2+(2-(1+\lambda_i)t_i)t_i\big)c_{i,1}+\lambda_it_i^2c_{i+1,1}\\\\
(4)&\lambda_i=\displaystyle\frac{\sqrt{|\triangle(c_{i,0},c_{i,1},c_{i+1,1})|}}{\sqrt{|\triangle(c_{i,0},c_{i,1},c_{i+1,1})|}+\sqrt{|\triangle(c_{i,1},c_{i+1,1},c_{i+1,2})|}}\\
\end{array}\right.

が満たされるようにベジェ制御点$c_{i,j}$を定めればよいことになります。
が、これをこのまま解析的に解くのは困難です。

##アルゴリズム
式(1)～(4)を使ってできることを並べてみると、

  • 全ての$c_{i,0}, c_{i,2}$があれば、(1)で全ての$t_i$を求められる
  • 全ての$\lambda_i, c_{i,1}$があれば、(2)で全ての$c_{i,0}, c_{i,2}$を求められる
  • 全ての$\lambda_i, t_i$があれば、(3)で全ての$c_{i,1}$を求められる
  • 全ての$c_{i,0},c_{i,1},c_{i,2}$があれば、(4)で全ての$\lambda_i$を求められる

となります。
これらをうまく組み合わせて、全ての$p_i$から全ての$c_{i,j}$を出力したいわけです。

概要

適当な初期値から始めて、何度も式を適用することで正解に近づけていく方針を取ります。

  • Step0. 各$\lambda_i,\ c_{i,j}$を初期化
  • Step1. 式(4)で各$\lambda_i$を算出・更新
  • Step2. 式(2)で各$c_{i,0}, c_{i,2}$を更新
  • Step3. 式(1)で各$t_i$を算出・更新
  • Step4. 式(3)で各$c_{i,1}$を更新
  • If 満足
    • then return $c_{i,j}$
    • else goto Step1.

各ステップに分けて見ていきましょう。

Step0. 初期化

以下のように初期化します。

  • $\lambda_i=0.5$
  • $c_{i,1}=p_i$
  • $c_{i,2}=c_{i+1,0} = (1-\lambda_i)c_{i,1}+\lambda_ic_{i+1,1} = (c_{i,1} + c_{i+1,1})/2$

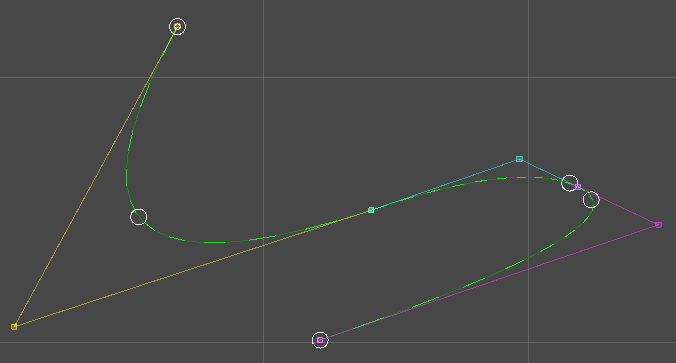
つまり、ユーザ制御点と中央のベジェ制御点が同じ場所にあり、
その他のベジェ制御点は隣接制御点の中点にある状態から始まります。
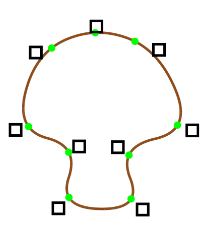
image.png
これは論文から引用した図で、初期化時の状態の例です。
黒い四角がユーザ制御点$p_i$で、$c_{i,1}$と一致しています。緑色の点は各セグメントの曲率極大点$c_i(t_i)$です。
今はまだ$p_i$と$c_i(t_i)$が離れていますが、この後のStep1～4のイテレーションを回すことで近づけていきます。
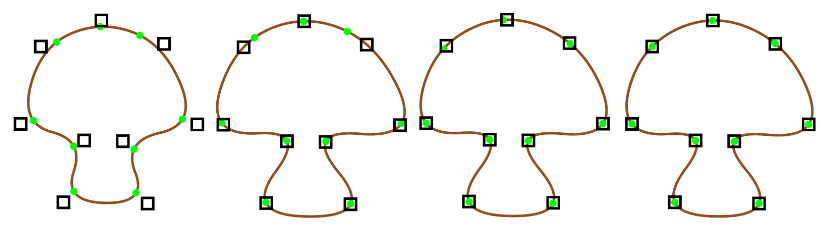
image.png
左から順に、初期状態、１ループ後、２ループ後、３０ループ後（完全収束）です。
ループ数は誤植ではなく、本当に数ループでほとんど完全収束と同じような形になります。

Step1. λの算出

式(4):

\lambda_i=\frac{\sqrt{|\triangle(c_{i,0},c_{i,1},c_{i+1,1})|}}{\sqrt{|\triangle(c_{i,0},c_{i,1},c_{i+1,1})|}+\sqrt{|\triangle(c_{i,1},c_{i+1,1},c_{i+1,2})|}}

を適用します。やるだけ。

Step2. ベジェ制御点（両端）の更新

式(2):

c_{i,2}=c_{i+1,0}=(1-\lambda_i)c_{i,1}+\lambda_ic_{i+1,1}

を計算します。これもやるだけ。

Step3. 曲率極大点の算出

式(1):

\|c'_{i,2}\|^2t_i^3-3c'_{i,2}p'_it_i^2+(2p_i'+c_{i,2}')p_i't_i-\|p_i'\|^2=0\ \ \ (c_{i,2}'=c_{i,2}-c_{i,0},\ p_i'=p_i-c_{i,0})

を解きます。カルダノの公式（三次方程式の解の公式）を組みましょう。
実解がただ一つ$[0,1]$に存在することが分かっています。

Step4. ベジェ制御点（中央）の更新

式(3):

p_i=(1-\lambda_{i-1})(1-t_i)^2c_{i-1,1}+\big(\lambda_{i-1}(1-t_i)^2+(2-(1+\lambda_i)t_i)t_i\big)c_{i,1}+\lambda_it_i^2c_{i+1,1}

を、全ての$c_{i,1}$について解きます。n元連立１次方程式ですね。
中学・高校の数学の範囲でも気合で解くことはできそうですが、行列を使うと簡単になります。

まず、係数を$\alpha_i, \beta_i, \gamma_i$として見やすく書き直しておきます。

p_i=\alpha_ic_{i-1,1}+\beta_ic_{i,1}+\gamma_ic_{i+1,1}

これは、以下のように行列表示の連立方程式にまとめることができます。

\left(\begin{matrix}
\beta_0&\gamma_0&&&\alpha_0\\
\alpha_1&\beta_1&\gamma_1&&\\
&&\ddots&&\\
&&\alpha_{n-2}&\beta_{n-2}&\gamma_{n-2}\\
\gamma_{n-1}&&&\alpha_{n-1}&\beta_{n-1}
\end{matrix}\right)
\left(\begin{matrix}
c_{0,1}\\
c_{1,1}\\
\vdots\\
c_{n-2,1}\\
c_{n-1,1}\\
\end{matrix}\right)
=
\left(\begin{matrix}
p_0\\
p_1\\
\vdots\\
p_{n-2}\\
p_{n-1}\\
\end{matrix}\right)

行列部分は三重対角行列＋角なので、高速にLU分解でき、解を$O(n)$で求めることができます。
さらに、これを上下に（行列は上下左右に）１つずつ拡張して

\left(\begin{matrix}
1&0&&&\\
\alpha_0&\beta_0&\gamma_0&&\\
&&\ddots&&\\
&&\alpha_{n-1}&\beta_{n-1}&\gamma_{n-1}\\
&&&0&1
\end{matrix}\right)
\left(\begin{matrix}
c_{n-1,1}\\
c_{0,1}\\
\vdots\\
c_{n-1,1}\\
c_{0,1}\\
\end{matrix}\right)
=
\left(\begin{matrix}
c_{n-1,1}\\
p_0\\
\vdots\\
p_{n-1}\\
c_{0,1}\\
\end{matrix}\right)

という形にすれば、行列部分はただの三重対角行列になるので、さらに計算が楽になります。

また、$n\ge5$の場合はメモリ的にも有利になります。
角つき三重対角行列はLU分解のためにメモリを$n\times n$要素分、頑張って削減しても$5\times n$要素分くらい食うのに対し、上下に伸ばした三重対角行列は$3\times (n+2)$要素分で済むのです。

LU分解については記事の最後の付録で解説します。

##実装
実際に実装していきましょう。
言語はC#で、座標表現やfloatの各種演算にUnityのVector2クラス、Mathfクラスを借りています。
Unity特有の何かがあるわけではないので、適宜好きな言語、好きなベクトル表現・数学ライブラリに置き換えてください。

ベジェ制御点用構造体

ただの配列のラッパーです。計算結果の出力もこのインスタンスで。
ベジェ制御点は隣接セグメント間で重複するので、配列サイズは重複を除いた最低限の$2n+1$とします。
ただ分かりにくいので、ここまでの解説に合わせて[i,j]でアクセスできるようにしておきます。
また、$n<3$の場合は点か直線を表示することが予想されるので、セグメント数を1とします。

public struct BezierControls
{
    //ベジェ制御点群
    //c_{0,0}, c_{0,1}, c_{1,0}, ..., c_{n-1,0}, c_{n-1,1}, c_{n-1,2}の順
    public Vector2[] Points { get; private set; }

    //セグメント数
    public int SegmentCount { get; private set; }

    //c_{i,j}
    public Vector2 this[int i, int j]
    {
        get => Points[2 * i + j];
        set => Points[2 * i + j] = value;
    }

    //コンストラクタ
    public BezierControls(int n)
    {
        SegmentCount = n < 3 ? 1 : n;
        Points = new Vector2[2 * SegmentCount + 1];
    }
}

計算空間の確保

ユーザ制御点が移動する度に描画を更新するわけなので、計算空間は事前に確保して使い回しましょう。
制御点が増減すると確保し直しになりますが、その辺りを考慮するとコードが煩雑になるのでここでは妥協。
Step4の行列計算時に使うメモリは三重対角部分だけで済むので、配列は$3(n+2)$要素だけ確保します。

public class CalcSpace
{
    public int N { get; private set; }              //制御点数
    internal float[] L { get; private set; }        //λ
    internal BezierControls C { get; private set; } //ベジェ制御点（出力）
    internal double[] T { get; private set; }       //t
    internal double[] A { get; private set; }       //Step4の行列計算用メモリ

    public CalcSpace(int n)
    {
        N = n;
        L = new float[n];
        C = new BezierControls(n);
        T = new double[n];
        A = new double[(n + 2) * 3];
    }
    public BezierControls Result => C;
}

ユーザ制御点・ベジェ制御点の上下拡張

Step4の行列計算時にユーザ制御点ベクトルとベジェ制御点ベクトルを上下拡張しますが、その際のメモリ確保をなくしつつちゃんと配列っぽく扱えるようにするためのラッパー構造体です。
コンストラクタで上下拡張時の値の初期化もやっています。
本質部分ではないしC#の人じゃないとたぶん意味が分からないので適当に読み飛ばしてください。

struct ExtendedPlayerControls
{
    Vector2 top;
    Vector2[] ps;
    Vector2 bottom;

    public Vector2 this[int i]
    {
        get => i == 0 ? top : i <= ps.Length ? ps[i - 1] : bottom;
        set
        {
            if (i == 0) top = value;
            else if (i <= ps.Length) ps[i - 1] = value;
            else bottom = value;
        }
    }

    public ExtendedPlayerControls(Vector2[] ps, BezierControls cs)
    {
        top = cs[cs.SegmentCount-1,1];
        this.ps = ps;
        bottom = cs[0,1];
    }
}
struct ExtendedBezierControls
{
    Vector2 top;
    Vector2[] cs;
    Vector2 bottom;

    public Vector2 this[int i]
    {
        get => i == 0 ? top : i <= cs.Length / 2 ? cs[i * 2 - 1] : bottom;
        set
        {
            if (i == 0) top = value;
            else if (i <= cs.Length / 2) cs[i * 2 - 1] = value;
            else bottom = value;
        }
    }

    public ExtendedBezierControls(BezierControls cs)
    {
        top = cs[cs.SegmentCount - 1, 1];
        this.cs = cs.Points;
        bottom = cs[0, 1];
    }
}

メソッドルート

処理の根本になる部分を作ります。

  • ユーザ制御点 points
  • 計算空間 space
  • イテレーション回数 iteration
  • 曲線をループさせるかどうか isLoop

を受け取り、Step0で初期化し、Step1～4でイテレーションを回し、最適化の結果を返します。
ただしユーザ制御点が２つ以下の場合は、それぞれ点や直線となるように制御点を配置して返します。

public static BezierControls CalcBezierControls(Vector2[] points, CalcSpace space, int iteration, bool isLoop)
{
    if (points.Length != space.N)
    {
        throw new ArgumentException($"The length of {nameof(points)} must equals to {nameof(space)}.{nameof(space.N)}.");
    }
    if (points.Length == 0)
    {
        for (int i = 0; i < 3; i++)
            space.C.Points[i] = Vector2.zero;
        return space.C;
    }
    if (points.Length == 1)
    {
        for (int i = 0; i < 3; i++)
            space.C.Points[i] = points[0];
        return space.C;
    }
    if (points.Length == 2)
    {
        space.C.Points[0] = points[0];
        space.C.Points[1] = (points[0] + points[1]) / 2;
        space.C.Points[2] = points[1];
        return space.C;
    }

    Step0(points, space.C, space.L, space.A, isLoop);
    for (int i = 0; i < iteration; i++)
    {
        Step1(space.C, space.L, isLoop);
        Step2(space.C, space.L);
        Step3(points, space.C, space.T);
        Step4(points, space.C, space.L, space.T, space.A, isLoop);
    }
    return space.C;
}

では、各Stepの実装をしましょう。
ループしない場合の対応も一緒にやっていきます。

Step0: 初期化

初期化内容はこうでした。

  • $\lambda_i=0.5$
  • $c_{i,1}=p_i$
  • $c_{i,2}=c_{i+1,0} = (1-\lambda_i)c_{i,1}+\lambda_ic_{i+1,1}$

非ループの場合、始端と終端はユーザ制御点であってほしいので、初期化時に固定してしまいましょう。

  • $\lambda_0=0$
  • $\lambda_{n-2}=1$
  • $\lambda_{n-1}=\rm{undefined}$

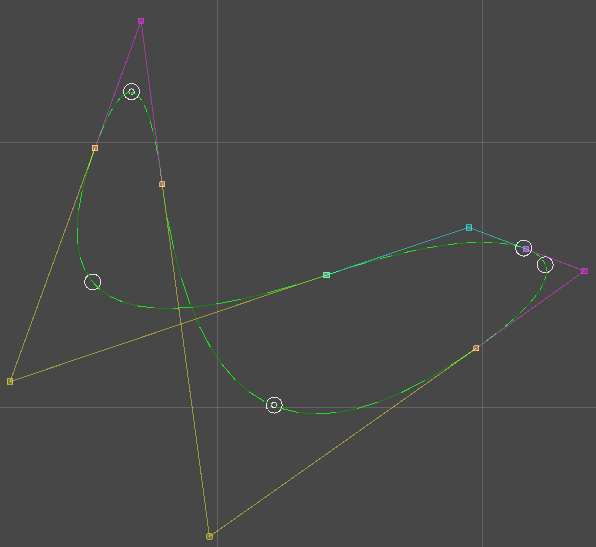
非ループの場合、終端→始端のカーブは必要なくなるので、ループの場合よりセグメントが２つ減ることに注意してください。その結果、$\lambda_{n-1}$は参照されなくなります。

セグメントが１つではなく２つ減るのは直感的ではありませんが、実際に見れば納得できるでしょう。
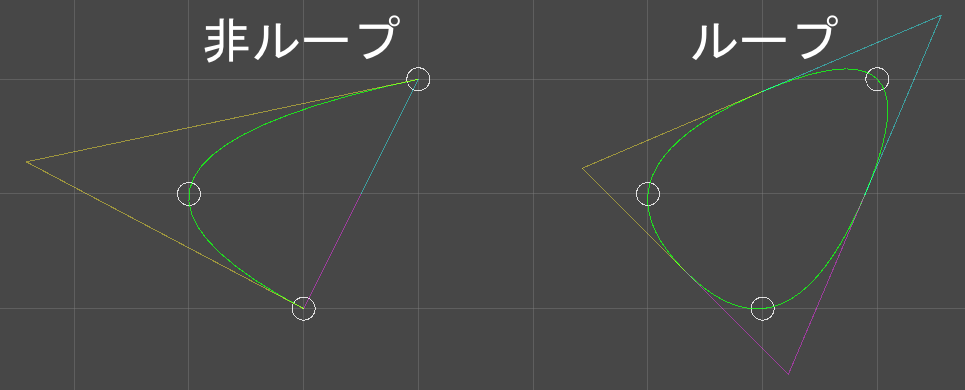
コメント 2020-02-04 122030.png
黄色・水色・ピンクの線が各セグメントのベジェ制御点を結んだものです。
非ループの場合、水色とピンクの線が潰れているのが分かるでしょうか。

ついでに、Step4で使う行列（の三重対角部分を保存するためのメモリ）の両端部の初期化もしてしまいます：

A=\left(\begin{matrix}
0&1&0\\
\alpha_0&\beta_0&\gamma_0\\
&\vdots&\\
\alpha_{n-1}&\beta_{n-1}&\gamma_{n-1}\\
0&1&0\\
\end{matrix}\right)

非ループの場合、$c_{0,1}=p_0,\ c_{n-1,1}=p_{n-1}$となればよいので、

A=\left(\begin{matrix}
0&1&0\\
0&1&0\\
\alpha_1&\beta_1&\gamma_1\\
&\vdots&\\
\alpha_{n-2}&\beta_{n-2}&\gamma_{n-2}\\
0&1&0\\
0&1&0\\
\end{matrix}\right)

とします。

コードはこんな感じ。

static void Step0(Vector2[] ps, BezierControls cs, float[] lambdas, double[] A, bool isLoop)
{
    var n = ps.Length;

    //全てのλを0.5で初期化
    for (var i = 0; i < n; i++)
        lambdas[i] = 0.5f;

    //ループしない場合、最初と最後から２番目を0,1に変更（最後はそもそも使わない）
    if (!isLoop)
    {
        lambdas[0] = 0;
        lambdas[n - 2] = 1;
        //lambdas[n - 1] = undefined;
    }

    //中央のベジェ制御点を全てユーザ制御点で初期化
    for (var i = 0; i < n; i++)
        cs[i, 1] = ps[i];

    //他のベジェ制御点を初期化
    for (var i = 0; i < n; i++)
    {
        var next = (i + 1) % n;
        cs[next, 0] = cs[i, 2] = (1 - lambdas[i]) * cs[i, 1] + lambdas[i] * cs[next, 1];
    }

    //行列の端の値は固定
    A[0] = 0;
    A[1] = 1;
    A[2] = 0;
    A[A.Length - 1] = 0;
    A[A.Length - 2] = 1;
    A[A.Length - 3] = 0;
    if (!isLoop)
    {
        //非ループの場合はさらにもう一行ずつ固定
        A[3] = 0;
        A[4] = 1;
        A[5] = 0;
        A[A.Length - 4] = 0;
        A[A.Length - 5] = 1;
        A[A.Length - 6] = 0;
    }
}

Step1: λの算出

\lambda_i=\frac{\sqrt{|\triangle(c_{i,0},c_{i,1},c_{i+1,1})|}}{\sqrt{|\triangle(c_{i,0},c_{i,1},c_{i+1,1})|}+\sqrt{|\triangle(c_{i,1},c_{i+1,1},c_{i+1,2})|}}

三角形の面積を求める解説は必要ないでしょう。外積の半分です。
非ループ時は始端と終端のλは更新しません。

static void Step1(BezierControls cs, float[] lambdas, bool isLoop)
{
    //三角形の面積を求める関数
    float TriArea(Vector2 p1, Vector2 p2, Vector2 p3)
    {
        p1 -= p3; p2 -= p3;
        return Mathf.Abs(p1.x * p2.y - p2.x * p1.y) / 2f;
    }

    var n = lambdas.Length;
    int begin = isLoop ? 0 : 1;
    int end = isLoop ? n : n - 2;
    for (var i = begin; i < end; i++)
    {
        var next = (i + 1) % n;
        var c = cs.Points;
        var t1 = TriArea(c[i*2], c[i*2+1], c[next*2+1]);
        var t2 = TriArea(c[i*2+1], c[next*2+1], c[next*2+ 2]);
        if (Mathf.Abs(t1 - t2) < 0.00001f)
            lambdas[i] = 0.5f;
        else
            lambdas[i] = (t1 - Mathf.Sqrt(t1 * t2)) / (t1 - t2);   
    }
}

Sqrt計算を減らすために一応有理化して、分母がほぼ0のときは計算させず0.5にしています。

なおκ-Curvesは３次元曲線にしても全く同じアルゴリズムで使えますが、外積の定義を３次元版（の絶対値）に変えるのを忘れないようにしましょう。

###Step2: ベジェ制御点（両端）の更新

c_{i,2}=c_{i+1,0}=(1-\lambda_i)c_{i,1}+\lambda_ic_{i+1,1}

やるだけです。
$\lambda_i$の方で非ループ対応はしているので、ここでは特に何もしません。

static void Step2(BezierControls cs, float[] lambdas)
{
    var n = lambdas.Length;
    for (var i = 0; i < n - 1; i++)
    {
        cs[i + 1, 0] = (1 - lambdas[i]) * cs[i, 1] + lambdas[i] * cs[i + 1, 1];
    }
    cs[0, 0] = cs[n - 1, 2] = (1 - lambdas[n - 1]) * cs[n - 1, 1] + lambdas[n - 1] * cs[0, 1];
}

※BezierControlsの実体は最後以外の$c_{i,2}$を削った配列なので、最後以外は片方だけに代入しています。

###Step3: 曲率極大点の算出
三次方程式：

\|c'_{i,2}\|^2t_i^3-3c'_{i,2}p'_it_i^2+(2p_i'+c_{i,2}')p_i't_i-\|p_i'\|^2=0\ \ \ (c_{i,2}'=c_{i,2}-c_{i,0},\ p_i'=p_i-c_{i,0})

を解きます。
三次方程式には解の公式（カルダノの公式）があるので、それを組みましょう。
複素解や$[0,1]$範囲外の実解は無視します。

なお、実解の範囲が分かっているので二分探索などをしてもよいですが、全体の計算時間が５倍くらいに跳ね上がります。オススメしません。

$ax^3+bx^2+cx+d=0$の$[0,1]$内の実解のみを返すカルダノの公式：

static double SolveCubicEquation(double a, double b, double c, double d)
{
    //負の値に対応した３乗根
    double Cbrt(double x) => Math.Sign(x) * Math.Pow(Math.Abs(x), 1.0 / 3);

    b /= a * 3;
    c /= a;
    d /= a;
    var p = c / 3 - b * b;
    var q = b * b * b - (b * c - d) / 2;
    var D = q * q + p * p * p;

    if (Math.Abs(D) < 1.0E-12) //D = 0
    {
        var ret = Cbrt(q) - b;
        if (ret >= 0)
            return Math.Min(ret, 1);
        else
            return Math.Min(ret * -2,1);
    }
    else if (D > 0)
    {
        var sqrtD = Math.Sqrt(D);
        var u = Cbrt(-q + sqrtD);
        var v = Cbrt(-q - sqrtD);
        var ret = u + v - b;
        return  ret < 0 ? 0 : ret > 1 ? 1 : ret;
    }
    else //D < 0
    {
        var tmp = 2 * Math.Sqrt(-p);
        var arg = Math.Atan2(Math.Sqrt(-D), -q) / 3;
        const double pi2d3 = 2 * Math.PI / 3;
        var ret1 = tmp * Math.Cos(arg) - b;
        if (0 <= ret1 && ret1 <= 1) return ret1;
        var ret2 = tmp * Math.Cos(arg + pi2d3) - b;
        if (0 <= ret2 && ret2 <= 1) return ret2;
        var ret3 = tmp * Math.Cos(arg - pi2d3) - b;
        if (0 <= ret3 && ret3 <= 1) return ret3;
        throw new Exception($"Invalid solution: {ret1}, {ret2}, {ret3}");
    }
}

参考：このページ

これを使って、全ての$i$について三次方程式を解きます。

ただし、そもそも三次方程式にならない場合の例外処理を忘れずに。
セグメントが潰れている場合に$a=b=c=d=0$となり不定解となります。ここでは$0.5$を入れておきます。
また、ユーザ制御点がセグメントの端にある場合には計算せずに$0,1$としましょう。

これらのフィルタリングの下では、$a$（と$d$）が非零であることが保証され、カルダノの公式が使えます。
ただし桁落ちでたまに破綻するので、実数の精度に気をつけましょう。

static void Step3(Vector2[] ps, BezierControls cs, double[] ts)
{
    for (int i = 0; i < ts.Length; i++)
    {
        //セグメントが潰れている場合は不定解なので0.5とする
        if(cs[i,0] == cs[i, 2]) { ts[i] = 0.5; continue; }
        //セグメントの端にユーザ制御点がある場合は図形的に自明
        if(ps[i] == cs[i, 0]) { ts[i] = 0; continue; }
        if(ps[i] == cs[i, 2]) { ts[i] = 1; continue; }

        var c2 = cs[i, 2] - cs[i, 0];   // != 0
        var p = ps[i] - cs[i, 0];       // != 0

        double a = c2.sqrMagnitude;             // != 0
        double b = -3 * Vector2.Dot(c2, p);     
        double c = Vector2.Dot(2 * p + c2, p);  
        double d = -p.sqrMagnitude;             // != 0

        ts[i] = SolveCubicEquation(a, b, c, d);
    }
}

余談ですが、上のカルダノの公式が例外を吐く場合は大体、範囲外ではなくNaNになっています。
不定解の例外処理を忘れているか、次のStep4でランク落ちを見過ごして発生したNaNがループで伝播してきている可能性が高いので、確認してみてください。

Step4: ベジェ制御点（中央）の更新

\left(\begin{matrix}
1&0&&&\\
\alpha_0&\beta_0&\gamma_0&&\\
&&\ddots&&\\
&&\alpha_{n-1}&\beta_{n-1}&\gamma_{n-1}\\
&&&0&1
\end{matrix}\right)
\left(\begin{matrix}
c_{n-1,1}\\
c_{0,1}\\
\vdots\\
c_{n-1,1}\\
c_{0,1}\\
\end{matrix}\right)
=
\left(\begin{matrix}
c_{n-1,1}\\
p_0\\
\vdots\\
p_{n-1}\\
c_{0,1}\\
\end{matrix}\right)

を解きます。ただし、

\begin{align}
\alpha_i&=(1-\lambda_{i-1})(1-t_i)^2\\
\beta_i&=\lambda_{i-1}(1-t_i)^2+(2-(1+\lambda_i)t_i)t_i\\
\gamma_i&=\lambda_it_i^2\\
\end{align}

です。
なお非ループの場合、$i=0,n-1$についてはStep0で初期化したように

\begin{align}
\alpha_0&=\alpha_{n-1}=0\\
\beta_0&=\beta_{n-1}=1\\
\gamma_0&=\gamma_{n-1}=0\\
\end{align}

で固定なので、上書きしないようにします。

まずは三重対角行列の連立方程式を解く関数を作っておきます。
三重対角行列のLU分解について、詳細は記事の最後に付録として載せてあります。

static void SolveTridiagonalEquation(double[] A, ExtendedBezierControls x, ExtendedPlayerControls b)
{
    var n = A.Length / 3 - 2;

    /* A=LU */
    for (int i=0, i3=0; i < n + 1; i++, i3+=3)
    {
        A[i3 + 3] /= A[i3 + 1];                 //l21  := a21/a11
        A[i3 + 4] -= A[i3 + 3] * A[i3 + 2];     //a'11 := a22-l21u12
    }
    
    /* Ly=b */            
    x[0] = b[0];                    //対角要素は全て1なので、最上行はそのまま            
    for (var i = 1; i < n + 1; i++) //対角要素の左隣の要素を対応するx（計算済み）にかけて引く
    {
        x[i] = b[i] - (float)A[i * 3] * x[i - 1];
    }

    /* Ux=y */
    x[n + 1] /= (float)A[(n + 1) * 3 + 1];              //最下行はただ割るだけ
    for (int i = n, i3 = n * 3; i >= 0; i--, i3 -= 3)   //対角要素の右隣の要素を対応するx（計算済み）にかけて引いて割る
    {
        x[i] = (x[i] - (float)A[i3 + 2] * x[i + 1]) / (float)A[i3 + 1];
    }
}

あとはAを組み立ててユーザ制御点・ベジェ制御点を上下拡張して実行するだけです。

が、一つ注意点として、上のアルゴリズムで解くためには**$A$はフルランクである必要があります。**
アルゴリズムに例外処理を加えてもいいですが、ここでは面倒なので$A$を微調整する方針でいきます。
$t_i=1\wedge t_{i+1}=0$の場合にランクが落ちるので、少しだけずらしてしまいましょう。
なおループしない場合、$t_{n-2}=1$や$t_1=0$でも同じことが起きます。

static void Step4(Vector2[] ps, BezierControls cs, float[] lambdas, double[] ts, double[] A, bool isLoop)
{
    var n = ps.Length;

    //係数行列Aを構成（端の部分はStep0で初期化済）
    {
        for (int i = isLoop ? 0 : 1; i < (isLoop ? n : (n-1)); i++)
        {
            var ofs = (i+1) * 3;
            var next = (i + 1) % n;
            var prev = (i - 1 + n) % n;

            //ランクが下がってしまう場合微調整
            if (ts[i] == 1 && ts[next] == 0 || !isLoop && i == n - 2 && ts[i] == 1)
                ts[i] = 0.99999f;
            if (!isLoop && i == 1 && ts[i] == 0)
                ts[i] = 0.00001f;


            var tmp = (1 - ts[i]) * (1 - ts[i]);
            A[ofs] = (1 - lambdas[prev]) * tmp;
            A[ofs + 1] = lambdas[prev] * tmp + (2 - (1 + lambdas[i]) * ts[i]) * ts[i];
            A[ofs + 2] = lambdas[i] * ts[i] * ts[i];
        }
    }

    //入出力ベクトルを拡張
    var extendedPs = new ExtendedPlayerControls(ps,cs);
    var extendedCs = new ExtendedBezierControls(cs);

    //連立方程式を解く
    SolveTridiagonalEquation(A, extendedCs, extendedPs);
}

プロット

これでκ-Curvesのシステムは完成ですが、まだベジェ曲線の制御点が算出できただけなので、描画する必要があります。
実際に画面に映すのは各描画ライブラリにやってもらうとして、そのための点群を用意しなければなりません。

とは言っても、各セグメントについて、↓これにtを順番に突っ込めばいいだけです。

c_i(t)=(1-t)^2c_{i,0} + 2(1-t)tc_{i,1} + t^2c_{i,2}

static Vector2 PlotSingle(Vector2 c0, Vector2 c1, Vector2 c2, float t)
{
    return (1 - t) * (1 - t) * c0 + 2 * (1 - t) * t * c1 + t * t * c2;
}

計算スペースのときのように、プロット用のスペースも確保しておきましょう。
セグメント数は非ループ時は２つ少なくなることに注意。
ユーザ制御点が２つ以下の場合の例外処理も忘れずに。

public class PlotSpace
{
    public int N { get; private set; }
    public int StepPerSegment { get; private set; }
    public Vector2[] Plots { get; private set; }

    public PlotSpace(int n, int stepPerSegment, bool isLoop)
    {
        N = n;
        StepPerSegment = stepPerSegment;
        if (n < 3)
            Plots = new Vector2[stepPerSegment + 1];
        else
            Plots = new Vector2[(isLoop ? n : (n - 2)) * stepPerSegment + 1];
    }
}

あとはプロッティングしていくだけ。
ベジェ曲線のちゃんとしたプロッティング手法としては、de Casteljauのアルゴリズムを使って曲率に応じて適応的に密度を変えるものが挙げられますが、ここでは面倒なので等間隔プロットとします。

public static Vector2[] CalcPlots(Vector2[] points, CalcSpace calcSpace, PlotSpace plotSpace, int iteration, int stepPerSegment, bool isLoop)
{
    //ベジェ制御点を計算
    var cs = CalcBezierControls(points, calcSpace, iteration, isLoop);

    //各セグメントについて、指定されたステップ数で分割した点を計算
    return CalcPlots(cs, plotSpace, stepPerSegment, isLoop);
}

public static Vector2[] CalcPlots(BezierControls cs, PlotSpace space, int stepPerSegment, bool isLoop)
{
    int offset, k;
    int segCnt = isLoop || cs.SegmentCount < 3 ? cs.SegmentCount : cs.SegmentCount - 2;
    for (k = 0; k < segCnt; k++)
    {
        offset = k * stepPerSegment;
        var nextk = (k + 1) % cs.SegmentCount;
        for (var i = 0; i < stepPerSegment; i++)
        {
            space.Plots[offset + i] = CalcPlotSingle(cs[nextk, 0], cs[nextk, 1], cs[nextk, 2], i / (float)stepPerSegment);
        }
    }
    var last = isLoop || cs.SegmentCount < 3 ? 0 : k;
    space.Plots[space.Plots.Length - 1] = CalcPlotSingle(cs[last, 0], cs[last, 1], cs[last, 2], 1);
    return space.Plots;
}

実行側

以上を全てKCurvesクラスに実装したとして、以下のようにすれば描画用の点群を取得できます。

//イテレーション回数
var iteration = 10;
//ループするかどうか
var isLoop = true;
//セグメントごとの分割数
var step = 20;

//ユーザ制御点を更新
Vector2[] input = /*更新処理*/;

//計算用空間確保（本来はキャッシュしておく）
var cSpace = new KCurves.CalcSpace(input.Length);
//プロット用空間確保（本来はキャッシュしておく）
var pSpace = new KCurves.PlotSpace(input.Length, step, isLoop);
//実行
var output = KCurves.CalcPlots(input, cSpace, pSpace, iteration, step, isLoop);

お疲れさまでした。

結果

Unity上で、１セグメントにつき20ステップで描画してみた結果です。
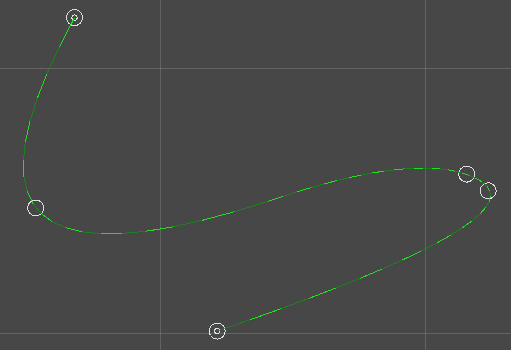
image.png

ベジェ制御点も表示してみるとこんな感じ。
image.png

同じ配置でループさせるとこうなります。
image.png

バグ？

はい、まだ終わってません。
ここまでの実装で実際に描画してみて、ユーザ制御点をめちゃくちゃ動かしまくってみると分かりますが、特定の状況下において適切な場所に収束しません。
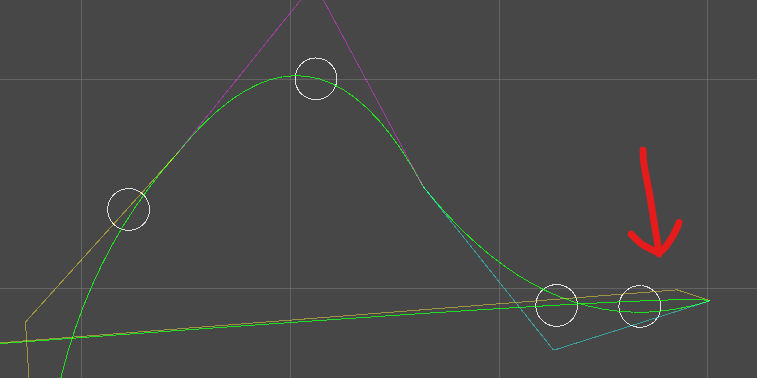
image.png
なんか、飛び出しています。よく見ると接続点の傾きも不連続になっています。
尖った領域かつユーザ制御点が近接している場合に起こりがちです。

この問題は、実は全ての条件を満たす解が存在しない場合がある（＝各条件を順番に解くだけでは収束しない）ことに起因します。

実用上は

  • Step1の回数を抑える
  • 最後にStep2を一度実行する

ことで解決しますが、真の最適解に収束しているわけではないことに注意しましょう。

public static BezierControls CalcBezierControls(Vector2[] points, CalcSpace space, int iteration, bool isLoop)
{
    //前略
    Step0(points, space.C, space.L, space.A, isLoop);
    for (int i = 0; i < iteration; i++)
    {
        if (i < 3 || i < iteration / 2)
            Step1(space.C, space.L, isLoop);
        Step2(space.C, space.L);
        Step3(points, space.C, space.T);
        Step4(points, space.C, space.L, space.T, space.A, isLoop);
    }
    Step2(space.C, space.L);
    return space.C;
}

結果：
image.png

それでも飛び出ることはある

具体的には、極薄極小のセグメントの存在が問題のようです。
例えばこんな場合。
新規キャンバス1.png

これはもう何というか、曲線ツールで鋭角を描こうとしているのが悪いです。
超鋭角の部分を検知して、その点で切断して２つのκ-Curvesに分けるといいかもしれません。

発展

記事公開から１年以上経ってもまだちょくちょく通知が来るので、新しい関連情報を少し追記します。

有理κ-Curves

通常の二次ベジェ曲線で定義できるなら、有理二次ベジェ曲線でもできるのでは？　と考えるのが自然です。
これは同じ筆頭著者の論文(Yan et al., 2019)で後に導入されています。
有理二次ベジェ曲線は円錐曲線全体をカバーするので、正確な円を描くこともできます（なので論文タイトルがCircle Reproduction～）。
またこちらの実装では最適化を全条件をまとめた式のエネルギー最小化で定義しており、前項で挙げた不安定性への対処もされています。
有理二次ベジェ曲線の（ほぼ）曲率連続な連結体なので、表現力はCAD等の用途でよく採用されるNURBS（非一様有理Bスプライン）と（ほぼ）同等と言えます。

A Class of C² Interpolating Splines

SIGGRAPH2020で、全く新しいスプライン曲線のクラスが提示されました。(Cem Yuksel, 2020)
ざっくりまとめると、隣接する３制御点$P_{i-1},P_{i},P_{i+1}$を繋ぐ曲線$F_i$を三角関数を使ってブレンドすることで、$F_i$によらず「至る所$C^2$連続かつ全ての制御点を通る」ことが保証された曲線を出力するものです。

$F_i$を適切に選ぶことで、曲率極大点を制御点に近づけることもできます（一致させるのは相当難しく、もしできたら論文が一本書けると思います）。
$F_i$としてκ-Curvesを用いるのが好例で、論文中でも紹介されています。

Yukselさんはこのクラスに特に名前をつけてくれておらず、論文等で引用する時に取り回しづらいのがちょっと難点。

#使用上の注意
Adobeが特許を取っているので、無断の商用利用はNGです。
何かに使う場合、特許権侵害にあたらないかは確認しておきましょう。

おわりに

κ-Curvesの実装は、大学で出た発展課題の一つでした。
そこで存在を知ったわけですが、非常に便利なので趣味のゲーム開発（非営利）にも流用しています。
修論のテーマにも影響したりと、個人的になかなか深く関わることになった曲線でした。
なお同じ講義を受けてググってこの記事に辿り着いた各位へ、脳死コピペはやめましょう。私はその講義の元TAです。

パラメトリック曲線界隈、最近ちょっと活発になった気がします。この間のVisual Computing 2020でもκ-Curves派生の新しいアイデアが発表されていましたね。
興味のある方は研究テーマにしてみてはいかがでしょうか。

#付録

三重対角行列のLU分解

まずLU分解とは、正方行列を下三角行列$L$と上三角行列$U$の積に分解する操作です。
$Ax=b$という連立方程式があるとき、$A=LU$とLU分解することで、$Ly=b$と$Ux=y$という２つの連立方程式に分離することができます。
三角行列の連立方程式は簡単に$O(n^2)$で解ける（前進代入・後退代入）ので、$A$がLU分解されていれば、ガウスの消去法を使った$O(n^3)$の解法より速くなります。
一般のLU分解は$O(n^3)$かかってしまうので、これは同じAを何度も利用する際にのみ有効な手段ですが、
$A$が三重対角行列の場合、LU分解もその後の計算も全て$O(n)$になります。

$L$の対角成分を1に固定しましょう。このとき、三重対角行列のLU分解$A=LU$の最初の様子は以下のように表せます。

\left(\begin{matrix}
a_{11}&a_{12}&&O\\
a_{21}&&&\\
&&A'&\\
O&&&
\end{matrix}\right)
=

\left(\begin{matrix}
1&&&O\\
l_{21}&&&\\
&&L'&\\
O&&&
\end{matrix}\right)

\left(\begin{matrix}
u_{11}&u_{12}&&O\\
&&&\\
&&U'&\\
O&&&
\end{matrix}\right)

成分を比較すると、

\begin{align}
a_{11}&=u_{11}\\
a_{12}&=u_{12}\\
a_{21}&=u_{11}l_{21}\\
A'&=L'U'+\left(\begin{matrix}
l_{21}u_{12}&\\
&O
\end{matrix}\right)
\end{align}

なので、

\begin{align}
u_{11}&=a_{11}\\
u_{12}&=a_{12}\\
l_{21}&=\frac{a_{21}}{a_{11}}\\
\end{align}

として

A'-\left(\begin{matrix}
l_{21}u_{12}&\\
&O
\end{matrix}\right)=L'U'

を再帰的にLU分解していけばよいことが分かります。
$O(1)$の$n$回ループなので$O(n)$です。

この計算では分解し終わった部分が後で必要になることはなく、さらに$L$の対角成分は全て1なので、$L$と$U$を重ね合わせることで$A$のメモリのみを使って分解できます。

\left(\begin{matrix}
a_{11}&a_{12}&&O\\
a_{21}&a_{22}&a_{23}&\\
&a_{32}&\ddots&\\
O&&&
\end{matrix}\right)
\rightarrow

\left(\begin{matrix}
u_{11}&u_{12}&&O\\
l_{21}&u_{22}&u_{23}&\\
&l_{32}&\ddots&\\
O&&&
\end{matrix}\right)

元が三重対角行列なので、$L,U$は共に各行２つ以下の要素しか持ちません。
そのため、前進代入・後退代入の計算量も$O(n)$となります。

角つき三重対角行列のLU分解

右上と左下に角がついている場合（行列サイズを拡張しない場合）も、少し複雑にはなりますが$O(n)$で分解できます。

\left(\begin{matrix}
a_{11}&a_{12}&O&a_{1n}\\
a_{21}&&&\\
O&&A'&\\
a_{n1}&&&
\end{matrix}\right)
=

\left(\begin{matrix}
1&&&O\\
l_{21}&&&\\
O&&L'&\\
l_{n1}&&&
\end{matrix}\right)

\left(\begin{matrix}
u_{11}&u_{12}&O&u_{1n}\\
&&&\\
&&U'&\\
O&&&
\end{matrix}\right)

成分を比較すると、

\begin{align}
u_{11}&=a_{11}\\
u_{12}&=a_{12}\\
l_{21}&=\frac{a_{21}}{a_{11}}\\
u_{1n}&=a_{1n}\\
l_{n1}&=\frac{a_{n1}}{a_{11}}\\
\end{align}

なので、

A'-\left(\begin{matrix}
\displaystyle\frac{a_{21}a_{12}}{a_{11}}&O&\displaystyle\frac{a_{21}a_{1n}}{a_{11}}\\
O&O&O\\
\displaystyle\frac{a_{n1}a_{12}}{a_{11}}&O&\displaystyle\frac{a_{n1}a_{1n}}{a_{11}}\\
\end{matrix}\right)=L'U'

となり、再帰的に分解できます。
ただし、$A'$のサイズが1のときはこの四隅は同じ位置を指すので、重複して引いてしまわないよう注意が必要です。

また、前進代入・後退代入も変わらず$O(n)$ではありますが、$L$は最下一行、$U$は最右一列が追加で埋まっています。
$L$も$U$も左からかけるので、この追加行・列の扱いは非対称的です。
$4\times 4$行列くらいの具体例で実際に手を動かしてみると実感できると思います。

具体例：

\left(\begin{matrix}
2&0&0&2\\
0&1&1&0\\
0&2&4&2\\
4&0&4&9\\
\end{matrix}\right)
\left(\begin{matrix}
1\\
2\\
3\\
4\\
\end{matrix}\right)
=
\left(\begin{matrix}
10\\
5\\
24\\
52\\
\end{matrix}\right)

\left(\begin{matrix}
2&0&0&2\\
0&1&1&0\\
0&2&4&2\\
4&0&4&9\\
\end{matrix}\right)
=
\left(\begin{matrix}
1&0&0&0\\
0&1&0&0\\
0&2&1&0\\
2&0&2&1\\
\end{matrix}\right)
\left(\begin{matrix}
2&0&0&2\\
0&1&1&0\\
0&0&2&2\\
0&0&0&1\\
\end{matrix}\right)

なお、一般の場合のLU分解や前進代入・後退代入についてはこちらのページなどに詳しく載っています。

（参考）パフォーマンス計測結果

私の環境でのパフォーマンス計測結果です。

n iteration time(ms)
30 5 0.1232
15 10 0.1177
30 10 0.2296
60 10 0.4564
120 10 0.9101
1000 10 7.516
環境
OS Windows10 Home
CPU Intel Core i7-8700
RAM 16GB
GPU NVIDIA GeForce GTX 970
その他 Unity2019.3.0f6上で実行

時間は10000回の平均値（四捨五入）で、CalcBezierControls()の時間のみを計測しています。

はい。$O(n\times \rm{iteration})$です。イテレーションは実用上は5～10回くらいで充分なので、C#実装でこれならそこそこ実用的な速度が出るかなと。

一応計測用コード（要Unity）：

[MenuItem("Tools/Test")]
static void _()
{
    int n = 30;
    int iter = 10;
    int loop = 10000;

    var path = new bool[n].Select(_ => new Vector2(Random.value, Random.value)).ToArray();
    var cSpace = new KCurves.CalcSpace(n);
    var sw = System.Diagnostics.Stopwatch.StartNew();
    for (int i = 0; i < loop; i++)
    {
        KCurves.CalcBezierControls(path, cSpace, iter, true);
    }
    Debug.Log((double)sw.ElapsedTicks / System.Diagnostics.Stopwatch.Frequency * 1000.0 / loop);
}

参考文献

元論文

Zhipei Yan, Stephen Schiller, Gregg Wilensky, Nathan Carr, and Scott Schaefer.
κ-curves: Interpolation at local maximum curvature.
ACM Transactions on Graphics, 36(4):129:1–129:7, 2017.
http://people.tamu.edu/~yanzp/projects/kCurves/kCurves.pdf

特許（Google Patents）

Fitting a parametric curve using maximum curvature
https://patents.google.com/patent/US9501848B2

関連

Zhipei Yan, Stephen Schiller, and Scott Schaefer.
Circle reproduction with interpolatory curves at local maximal curvature points.
Computer Aided Geometric Design, 72:98 – 110, 2019.
http://people.tamu.edu/~yanzp/projects/ratkappa/ratk.pdf

Cem Yuksel.
A class of c2 interpolating splines.
ACM Transactions on Graphics, 39(5):160:1–160:14, jul 2020.
http://www.cemyuksel.com/research/interpolating_splines/

わかりやすいNURBS解説
https://www.unisys.co.jp/tec_info/tr114/11403.pdf

Solving Cubic Equations
http://www.1728.org/cubic2.htm

  1. 3D曲線の場合、曲率は絶対値を取って扱うことが多いようです。2D曲線でも絶対値つきで定義されていることがあるかもしれませんが、ここではκ-Curvesの論文に倣って符号付きとします。 ↩

297
259
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
297
259

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?