シミュレーションマニア(1) レストランでの座席案内をシミュレーションで再現してみた

はじめに

シミュレーションって面白い．ということで，これから時々，身近にある様々な題材を取り上げ，その様子を簡単なシミュレーションで表現したらどうなるかを紹介していこうと思う．今回は，最初の題材として，レストランの座席案内を取りあげる．

モデルの概要

レストランの店内には2人用のテーブルが直列に7台並んでいるとする．顧客は，1人から7人までのグループでランダムにやってきて，座席に案内されるのを待つ．3人以上のグループは1つのテーブルには収容しきれないので，複数のテーブルを組み合わせて座ってもらう．このとき，組み合わせることができるのは隣り合ったテーブルのみとしよう．

待ち行列が長いと，顧客は列には並ばずに諦めて帰ってしまう．座席に案内された顧客は，食事を済ませると帰っていく．食事にかかる時間は正規分布に従う乱数で与えることにしよう．

座席案内は，ひとまず，先着順（First-In-First-Out）で，空いている席からランダムに案内する席を決めるという（少し乱暴な）ルールに従うと考える．

この条件でシミュレーションを行ってみたのが下の例である（いつか動画に差替えたい）．

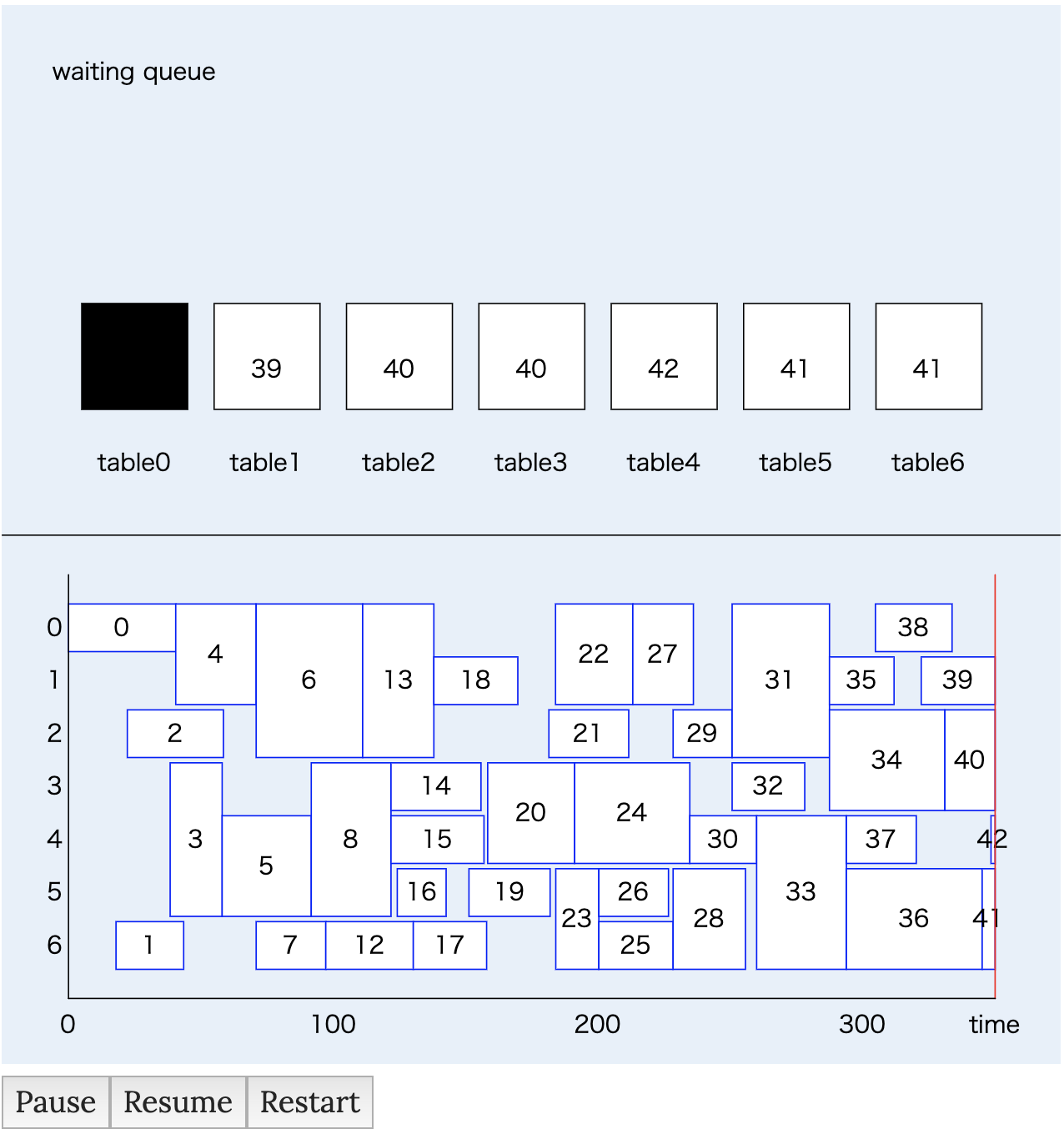
上半分の部分にある四角形がテーブルを表している．テーブル内の数字は顧客の番号である．大勢のグループが来ると，隣り合った複数のテーブルを専有している様子が見られる．テーブルが黒色に変わっている間は，そこが空席になっていることを表している．また，時々テーブルの上に現れる円は，待ち行列を表している．

下半分に現れる図は，いわゆるガントチャートである．横軸が時間で，縦軸がテーブル番号に対応しており，どのタイミングでどの顧客がどのテーブルを使用していたかがわかる．

この図を見ると，座席案内は並列機械スケジューリング問題に似ていることがわかる．テーブルが直列に配置されている場合，主な相違点は，ジョブが隣り合った複数の機械を同時に専有する場合があるということである．

現実には，目的関数にも特徴がある．単にテーブルの回転率を向上させることだけではなく，案内されるまでの待ち時間や案内される座席についての顧客の満足度（不満度？）にも気を配る必要がある．

上記のようなシミュレーションを利用すると，そうした複眼的な観点から，座席案内ルールの比較なども行えるだろう．

コードの概説

コードの大枠は，以前にここで説明したフレームワークに則っている．コードの全体像は，このGitHubのリポジトリのsim/static/code/mania/code01.jsに置くので，必要に応じて参照してほしい．ここでは，主なポイントだけ見ておこう．

まず，モデルオブジェクトのコンストラクタは下記のようになっている．

function Model() {
  this.par = {
    NT: 7,  // number of tables
    MTB: 10,  // mean time between arrivals
    MET: 30,  // mean eating time
    SD: 8,  // standard deviation
  };
  this.customers = new Customers();
  this.tables = new Tables(this.par.NT);
  this.calendar = new Calendar([
    {time:0, type:"arrival"},  // arrival of the 1st customer
    {time:350, type:"over"}  // the end of simulation
  ]);
}

モデルの構成要素として，Cutomers，Tables，Calendarの3つのオブジェクトがあることがわかる．また，parには，テーブル数（NT），顧客の平均到着間隔（MTB），食事時間の平均（MET）と標準偏差（SD）のパラメータが与えてある．

Calendarはここで説明したものをそのまま再利用しているだけなので省略し，他の2つのオブジェクトについて確認しておく．まず，Customersは下記のようになっている．

function Customer(id, now) {
  this.id = id;
  this.size = this.set_size();  // how many people are you?
  this.place = undefined;  // where are you now?
  this.table = [];  // table(s) assigned
  this.arrived = now;  // when arrived
  this.seated = undefined;  // when seated
  this.left = undefined;  // when left
}

function Customers() {
  this.num = 0;
  this.waiting_people = 0;
  this.balked = [];  // customers who left without waiting
  this.queued = [];  // customers who are waiting in the queue
  this.served = [];  // customers who are being served at tables
  this.left = [];  // customers who left after finishing meal
}

上の部分で，番号（id），人数（size），居場所（place），割り当てられたテーブルのリスト（table），到着時刻（arrived），着席時刻（seated），退店時刻（left）の情報を持ったCustomerオブジェクトが定義してある．

そして，下のCustomers（複数形）の方には，来店した顧客グループの総数（num）と待ち行列の長さ（waiting_people）のほか，列に並ばずに帰った顧客のリスト（balked），待ち行列に並んでいる顧客のリスト（queued），店内で着席している顧客のリスト（served），食事を終えて退店した顧客のリスト（left）を持たせてあることがわかる．

一方，Tablesは下記のようになっている．

function Table(id) {
  this.id = id;
  this.free = true;  // if not, this table is occupied
  this.who = undefined;  // customers at this table
}

function Tables(N) {  // N: total number of tables
  this.tables = [];
  for(var i = 0; i < N; i ++) {  // serially located tables
    this.tables.push(new Table(i));
  }
}

上の部分で，番号（id），空き状況（free），着席している顧客（who）の情報を持ったCustomerオブジェクトが定義してある．そして，下の部分にあるTables（複数形）にはTableのリストが与えられていることがわかる．

続いて，主なメソッドを見てみる．まず，イベント駆動でモデルの状態を変化させていくプロセスの大枠を取り仕切っているのがupdate()メソッドである．

Model.prototype.update = function() {
  var e = this.calendar.fire();  // e: the next event
  if(e.type == "over") {
    noLoop();  //  simulation is over
  } else if(e.type == "arrival") {
    this.customers.arrive(e.time);
    this.calendar.extend({
      time: e.time +exp_rand(1 /this.par.MTB),
      type: "arrival"  // arrival of next customer
    });
    this.seat_customers(e.time);
  } else if(e.type == "departure") {
    this.customers.leave(e.who, e.time);
    this.seat_customers(e.time);
  }
}

Calendarから次のイベントを取り出し，その種類に応じた処理を施していることがわかる．生起するイベントがoverなら，p5.jsのnoLoop()を呼んでdraw()のループを止めている．

arrivalなら，customersのarrive()メソッドを呼んだ後，次のarrivalイベントをCalendarに追加した上で，モデルのseat_customers()メソッドを呼び出す．departureならcustomersのleave()メソッドを呼んだ後，同じくモデルのseat_customers()メソッドを呼び出す．

arrive()メソッドとleave()メソッドは下記のようになっている．

Customers.prototype.arrive = function(now) {  // arrive at restaurant
  var c = new Customer(this.num, now);
  this.num ++;
  if(this.waiting_people > 10) {  // (too) simple balking rule
    c.left = now;
    c.place = "balked";
    this.balked.push(c);
  } else {
    c.place = "queued";
    this.queued.push(c);
    this.waiting_people += c.size;
  }
}

まず，arrive()の方では，新しい顧客がレストランに到着する様子を表している．新規顧客のオブジェクトを生成し，顧客の総数をインクリメントした後，待ち行列の長さに応じて，諦めて帰るか，列に並ぶかの処理を施しているがわかる．

Customers.prototype.leave = function(c, now) {  // finish meal & leave restaurant
  c.left = now;
  c.place = "left";
  this.left.push(c);
  for(var i = 0; i < this.served.length; i ++) {
    if(this.served[i] == c) {
      this.served.splice(i, 1);
      break;
    }
  }
  for(var t of c.table) {
      t.free = true;
      t.who = undefined;
  }
}

leave()の方では，単純に当該顧客をservedのリストからleftのリストに移動させ，使用していたテーブルの状態を「空き」に変更している．

また，seat_customers()メソッドは下記のようになっている．

Model.prototype.seat_customers = function(now) {
  while(this.customers.queued.length > 0) {  // are there waiting customer(s)?
    var c = this.customers.queued[0];  // 1st customer in the queue
    var table_num = ceil(c.size /2);  // how many tables needed?
    var candidates = this.tables.get_candidates(table_num);
    if(candidates.length == 0) {
      return;
    }
    c.table = random(candidates);  // (too) simple seating rule
    this.customers.take_seat(c, now);
    this.calendar.extend({
      time: now +tnorm_rand(this.par.MET, this.par.SD),
      type: "departure",
      who: c  // customer c finishes meal
    });
  }
  return;
}

もし待ち行列に待っている顧客がいれば，その先頭の顧客に注目し，必要なテーブル数を計算した後，それだけの数の空きテーブルを並びで確保できる組合せの候補をget_candidates()メソッド（詳細は省略する）で探してくる．

その結果，候補が見つけられなければ何もせずにreturn．見つけられた場合は，候補の中からランダムに組合せを1つ選択し，その組合せのテーブルに先頭の顧客を案内する．

これを待ち行列が空になるか，候補が見つからずにreturnになるかのいずれかの状態に至るまでwhileループで繰り返している．

なお，テーブルに案内する部分の具体的な処理は下のtake_seat()メソッドが担っている．

Customers.prototype.take_seat = function(c, now) {  // seated to a table
  c.seated = now;
  c.place = "served";
  this.served.push(c);
  for(var i = 0; i < this.queued.length; i ++) {
    if(this.queued[i] == c) {
      this.queued.splice(i, 1);
      this.waiting_people -= c.size;
      break;
    }
  }
  for(var t of c.table) {
      t.free = false;
      t.who = c;
  }
}

すでに説明したleave()メソッドに似ているので，詳細な説明は不要だろう．

まとめ

今回は，レストランでの座席案内の様子を非常に単純なモデルに落とし込んで，シミュレーションで再現してみた．このモデルを実態に応じて拡張すれば，実店舗での業務分析や，担当者のスキル評価や習熟支援などにも活用できる可能性があるかもしれない．