Linear Conflict A* Search in Dogelog Player

Last updated at 2024-05-29Posted at 2024-05-29

Introduction

Dogelog Player is a Prolog system 100% written in Prolog itself. It is unique among Prolog systems in that it does not have a concept of a stack frame, so a DEC10 ancestor/1 built-in or even error backtraces are not available by design.

We were interested in a larger example to see whether this design pays off. In the following we show an implementation of Linear Conflict A* Search to solve 8-puzzles and compare with newer Prolog systems such as Scryer Prolog and Trealla Prolog.

A* Search

A* is an extension of Dijkstra's algorithm with some characteristics of breadth-first search (BFS). A* expands paths that are already less expensive by using this function:

f(n) = g(n) + h(n).

g(n) = cost so far to reach node n.
h(n) = estimated cost from n to goal.

We use a relatively slim tail recursive solution, where we carry around the path in the form of a list of puzzle movements. Using length/2 on the list gives us already the g(n) part. The h(n) part is the predicate weight/2:

astar(S, L, _, _, L) :- goal(S), !.
astar(S, L, A, V, R) :-
   length(L, N),
   findall(W-(T,[M|L]), (move(S,T,M), \+ member(T, V), 
         weight(T,J), W is J+N), B),
   insert(B, A, [_-(T,H)|D]),
   astar(T, H, D, [T|V], R).

The predicate insert/3, implements a straight forward bulk insertion based on linear scanning the queue list. This has still good performance for large priority queues, since expansion typically happens among the front lower weights.

Manhattan Distance

The efficiency of A* search not only hinges on the efficiency of the priority queue but also on the efficiency of the heuristic function. Manhattan Distance is a popular heuristic for the 8-puzzle which can be implemented via keysort/2:

% weight(+State, -Integer)
weight(T, W) :-
   positions(T, 0, S),
   keysort(S, R),
   score(R, 0, W).

% positions(+State, +Integer, +Pairs)
positions([], _, []).
positions([X|L], J, [X-J|R]) :-
   K is J+1,
   positions(L, K, R).

% score(+Pairs, +Integer, -Integer)
score([], _, 0).
score([_-I|R], J, W) :-
   K is J+1,
   score(R, K, V),
   W is abs(I div 3-J div 3)+abs(I mod 3-J mod 3)+V.

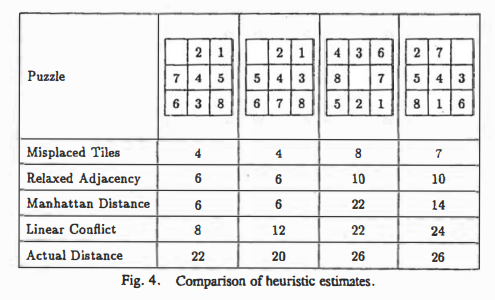
Compared to the Hamming Distance which is not extremely efficient, the Manhattan Distance makes it feasible to solve the 8-puzzle in less than a minute. We find for our two running examples:

?- start(X), time(astar(X, [], [], [], L)), length(L, N).
% 13,959,316 inferences, 0.891 CPU in 0.895 seconds (100% CPU, 15673618 Lips)
X = [6, 1, 3, 4, -1, 5, 7, 2, 0],
L = [left, left, up, right, right, down, left, left, up|...],
N = 26.

?- X = [-1, 7, 6, 5, 4, 3, 2, 1, 0], time(astar(X, [], [], [], L)), length(L, N).
% 231,210,079 inferences, 15.172 CPU in 15.153 seconds (100% CPU, 15239387 Lips)
X = [-1, 7, 6, 5, 4, 3, 2, 1, 0],
L = [up, left, left, down, right, up, right, down, left|...],
N = 30.

Linear Conflict

One gets an itch more heuristic power by adding on top of Manhattan distance a goal conflict measure. It was publish in 1992 by Hansson, Mayer and Yung:

We borrowed Kuniaki Mukais bubblesort, which he uses to count inversions. And modified it so that it gives us some linear conflict measure:

% bubblesort(+Pairs, -Pairs, -List, +List)
bubblesort([],[]) --> [].
bubblesort([X|Y],Z) -->
	bubblesort(Y,V),
	insert(X,V,Z).

% insert(+Pair, -List, +List)
insert(X,[],[X]) --> !.
insert(X-P,[Y-Q|Z],[X-P,Y-Q|Z]) --> {X<Y}, !.
insert(X-P,[Y-Q|Z],[Y-Q|U]) --> kind(X,Y), insert(X-P,Z,U).

% kind(+Integer, +Integer, -List, +List)
kind(P, Q) --> {P div 3 =:= Q div 3}, !, [*].
kind(P, Q) --> {P mod 3 =:= Q mod 3}, !, [*].
kind(_, _) --> [].

We were then weighting the measure by 1/3. This alternative heuristic gives again some additional speed to slagos and the reverse example. Further it seems to give still optimum solutions:

?- start(X), time(astar(X, [], [], [], L)), length(L, N).
% 6,431,573 inferences, 0.453 CPU in 0.457 seconds (99% CPU, 14193816 Lips)
X = [6, 1, 3, 4, -1, 5, 7, 2, 0],
L = [left, left, up, right, right, down, left, left, up|...],
N = 26.

?- X = [-1, 7, 6, 5, 4, 3, 2, 1, 0], time(astar(X, [], [], [], L)), length(L, N).
% 50,214,313 inferences, 3.500 CPU in 3.504 seconds (100% CPU, 14346947 Lips)
X = [-1, 7, 6, 5, 4, 3, 2, 1, 0],
L = [up, left, left, down, right, up, right, down, left|...],
N = 30.

Systems Comparison

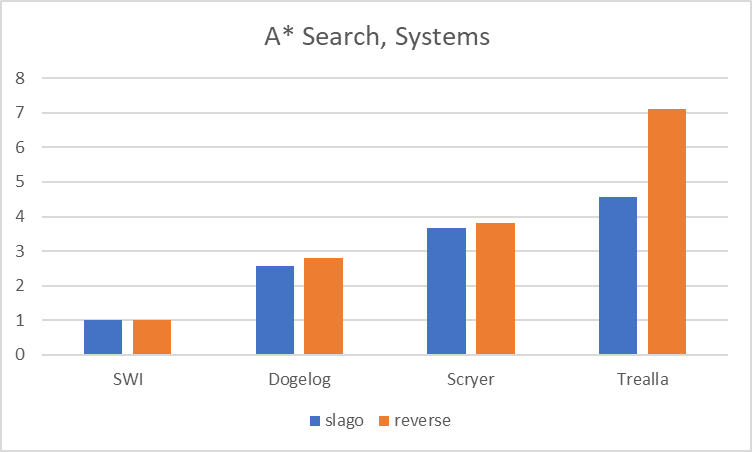
Our measurements so far were done with SWI-Prolog 9.3.2 on a Windows 10 machine. We were then currious how Dogelog Player 1.2.1 performs. Usually Dogelog Player is around 4 times slower than SWI-Prolog. In this example Dogelog Player approaches SWI-Prolog by a factor 2-3 times.

We compared our Java implementation to Scryer-Prolog 0.9.4 and Trealla Prolog 2.52.15. The former Prolog system is a Rust implementation, and the later Prolog system is a C implementation. We leave behind both Prolog systems, and unlike Trealla Prolog we are not bugged by some break out in the 2nd test.

Conclusions

One gets an itch more heuristic power by adding on top of Manhattan distance a goal conflict measure. Performance wise SWI-Prolog still leads the pack, but we leave behind both Scryer-Prolog and Trealla Prolog. Interestingly we are also not bugged by some break out in the 2nd test.